5.10: Від метрики до кривизни
- Page ID
- 77774
Пошук символу Крістоффеля з метрики
Ми вже знайшли символ Крістоффеля з точки зору метрики в одному вимірі. Висловлюючи його в тензорних позначеннях, ми маємо
\[\Gamma^{d}_{ba} = \frac{1}{2} g^{cd} (\partial_{?} g_{??}),\]
де інверсія однокомпонентної матриці G була замінена інверсією матриці, і, що ще важливіше, знаки питання вказують на те, що було б кілька способів розмістити індекси так, щоб результатом було граматичне тензорне рівняння. Найбільш загальною формою для символу Крістоффеля було б
\[\Gamma^{b}_{ac} = \frac{1}{2} g^{db} (L \partial_{c} g_{ab} + M \partial_{a} g_{cb} + N \partial_{b} g_{ca}),\]
де\(L\)\(M\), і\(N\) є константами. Послідовність з одновимірним виразом вимагає
\[L + M + N = 1\]
і зникає кручення дає\(L = M\). \(M\)Терміни\(L\) та терміни мають інше фізичне значення, ніж\(N\) термін.
Припустимо, спостерігач використовує такі координати, що всі об'єкти описуються як подовження з часом, а зміна масштабу, накопиченого за один день, є коефіцієнтом k > 1. Це описується похідною\(\partial_{t} g_{xx}\) < 1, яка впливає на\(M\) термін. Оскільки метрика використовується для обчислення квадратних відстаней, елемент матриці g xx зменшується на\(\frac{1}{\sqrt{k}}\). Щоб компенсувати\(\partial_{t} v^{x} < 0\), тому нам потрібно додати позитивний термін корекції\(M > 0\), до коваріантної похідної. Коли той самий спостерігач вимірює швидкість зміни\(v^t\) вектора щодо простору, швидкість зміни виявляється занадто маленькою, оскільки змінна, яку вона диференціює щодо, занадто велика. Для цього потрібно\(N < 0\), і корекція буде того ж розміру, що і\(M\) корекція, так\(|M| = |N|\). Знаходимо\(L = M = −N = 1\).
Вправа\(\PageIndex{1}\)
Чи залежить вищевказаний аргумент від використання простору для однієї координати і часу для іншої?
Отриманий загальний вираз для символу Крістоффеля в терміні метрики дорівнює
\[\Gamma^{c}_{ab} = \frac{1}{2} g^{cd} (\partial_{a} g_{bd} + \partial_{b} g_{ad} - \partial_{d} g_{ab}) \ldotp\]
Можна легко повернутися назад і перевірити, що це дає
\[\nabla_{c} g_{ab} = 0. \label{eq10}\]
Підтвердження рівняння\ ref {eq10} трохи втомлює. З цього приводу тензорні обчислення в цілому можуть бути ганебно трудомісткими та схильними до помилок. Будь-яка розумна людина, що живе в 21 столітті, тому вдасться до системи комп'ютерної алгебри. Найбільш широко використовуваною системою комп'ютерної алгебри є Mathematica, але вона дорога і власна, і вона не має великих вбудованих засобів для обробки тензорів. Виявляється, вільного тензорного програмного забезпечення з відкритим вихідним кодом досить багато, і воно поділяється на два класи: координатно-незалежний і координатно-незалежний. Найкращий доступний незалежний від координати з відкритим вихідним кодом об'єкт є Кадабра, і насправді перевірка\(\nabla_{c} g_{ab}\) = 0 є першим прикладом, наведеним у зручному посібнику Лео Брювіна щодо застосувань Кадабри до загальної відносності. 13
Вправа\(\PageIndex{2}\)
У випадку 1 виміру, показати, що це зводиться до більш раннього результату\(−(\frac{1}{2}) \frac{dG}{dX}\).
Оскільки\(\Gamma\) це не тензор, то не очевидно, що коваріантна похідна, яка побудована з нього, є тензором. Але якщо це не очевидно, це також не дивно - мета вищевказаного деривації полягала в тому, щоб отримати результати, які були б незалежними від координат.
Приклад 10: Символи Крістоффеля на земній кулі, кількісно
У прикладі 9 ми зробили висновок наступні властивості символу Крістоффеля\(\Gamma^{\theta}_{\phi \phi}\) на сфері радіуса R:\(\Gamma^{\theta}_{\phi \phi}\) незалежний від\(\phi\) і R,\(\Gamma^{\theta}_{\phi \phi}\) < 0 у північній півкулі (colatitude θ менше π/2),\(\Gamma^{\theta}_{\phi \phi}\) = 0 на екваторі та\(\Gamma^{\theta}_{\phi \phi}\) > 0 у південна півкуля.
Метрика на сфері
\[ds^2 = R^2 d\theta^{2} + R^2 \sin^2 \theta d\phi^{2}.\]
Єдиним терміном, що не зникає у виразі for\(\Gamma^{\theta}_{\phi \phi}\), є той, який включає\(\partial_{\theta} g_{\phi \phi} = 2R^{2} \sin \theta \cos \theta\). Результат
\[\Gamma^{\theta}_{\phi \phi} = − \sin \theta \cos \theta\]
які можна перевірити, щоб мати властивості, заявлені вище.
Чисельне розв'язання геодезичного рівняння
У розділі 5.7 я дав алгоритм, який продемонстрував унікальність розв'язків геодезичного рівняння. Цей алгоритм також може бути використаний для пошуку геодезичних робіт у випадках, коли метрика відома. Наступна програма, написана на комп'ютерній мові Python, здійснює дуже простий розрахунок такого роду, в разі, коли ми знаємо, якою має бути відповідь; навіть без будь-якого попереднього знайомства з Python, не повинно бути важко побачити відповідність між абстрактним алгоритмом, представленим в Розділ 5.7 та його конкретна реалізація нижче. Для полярних координат в евклідовій площині можна обчислити\(\Gamma^{r}_{\phi \phi}\) = −r і\(\Gamma^{\phi}_{r \phi} = \frac{1}{r}\) (задача 2). Тут ми обчислюємо геодезичний, який починається дотичною до одиничного кола в\(\phi=0\).

Не варто турбуватися про всі технічні деталі мови (наприклад, рядок 1, що робить доступними такі зручності, як math.pi for\(\pi\)). Коментарі зазначаються знаками фунта. Рядки 16-34 мають відступ, тому що всі вони повинні виконуватися повторно, поки це більше не вірно\(\lambda < \lambda_{max}\) (рядок 15).
Вправа\(\PageIndex{3}\)
Оглянувши лінії 18-22, знайдіть знаки\(\ddot{r}\) і\(\ddot{\phi}\) при\(\lambda\) = 0. Переконайте себе, що ці знаки - це те, чого ми очікуємо геометрично.
Вихід виглядає наступним чином:

Ми бачимо, що\(\phi\) → 90 град. як\(\lambda \rightarrow \infty\), що має сенс, тому що геодезична є прямою лінією, паралельною осі y. Менш тривіальне використання методики продемонстровано в розділі 6.2, де ми обчислюємо відхилення світлових променів у гравітаційному полі, одному з класичних спостережних тестів загальної теорії відносності.
Тензор Рімана з точки зору символів Крістоффеля
Коваріантну похідну вектора можна інтерпретувати як швидкість зміни вектора в певному напрямку, відносно результату паралельного транспортування вихідного вектора в тому ж напрямку. Тому ми можемо бачити, що визначення тензора кривизни Рімана в розділі 5.4 є мірою нездатності коваріантних похідних комутувати:
\[(\nabla_{a} \nabla_{b} - \nabla_{b} \nabla_{a}) A^{c} = A^{d} R^{c}_{dab}\]
Нудний розрахунок тепер дає з\(R\) точки зору\(\Gamma\) s:
\[R^{a}_{bcd} = \partial_{c} \Gamma^{a}_{db} - \partial_{d} \Gamma^{a}_{cb} + \Gamma^{a}_{ce} \Gamma^{e}_{db} - \Gamma^{a}_{de} \Gamma^{e}_{cb}\]
Це наводиться як інший приклад пізніше в посібнику Бревіна щодо застосування Кадабри до загальної теорії відносності. 14 (Brewin записує верхній індекс у другому слоті R.)
Деякі загальні ідеї про Gauge
Давайте відступимо зараз на мить і спробуємо отримати деяке фізичне розуміння, дивлячись на особливості, які мають загальні електромагнітні та релятивістські калібрувальні перетворення. У нас є такі аналогії:
| електромагнетизм | диференційна геометрія | |
|---|---|---|
| глобальна симетрія | Постійний зсув фаз не\(\alpha\) має спостережуваних ефектів. | Додавання константи до координати не має спостережуваних ефектів. |
| локальна симетрія | Зсув фаз\(\alpha\), який змінюється від точки до точки, не має спостережуваних ефектів. | Довільне перетворення координат не має спостережуваних ефектів. |
| Калібр описується. | \(\alpha\) | \(g_{\mu \nu}\) |
| . і диференціація цього дає калібрувальне поле. | А б | \(\Gamma^{c}_{ab}\) |
| Друга диференціація дає безпосередньо спостережуване поле (и). | Е і Б | \(R^c_{dab}\) |
Цікавим є те, що поля, що безпосередньо спостерігаються, не несуть всієї необхідної інформації, але поля калібрування безпосередньо не спостерігаються. В електромагнетизмі ми можемо бачити це з ефекту Агаронова-Бома, показаного на малюнку\(\PageIndex{1}\). 15 Електромагнітний соленоїд має B = 0 зовні, і електронні пучки коли-небудь рухаються лише через зовнішню область, тому вони ніколи не відчувають магнітного поля. Експерименти показують, однак, що включення і виключення соленоїда змінює перешкоди між двома променями. Це пов'язано з тим, що векторний потенціал не зникає поза соленоїдом, і, як ми бачили в розділі 4.2, фаза пучків змінюється відповідно до шляху інтеграла A b. Тому нам залишається незручна, але неминуча ситуація. Поняття поля повинно усунути необхідність миттєвої дії на відстані, що заборонено відносністю; тобто (1) ми хочемо, щоб наші поля мали лише локальні ефекти. З іншого боку, (2) ми хотіли б, щоб наші поля були безпосередньо спостережуваними величинами. Ми не можемо мати як 1, так і 2. Поле калібрування задовольняє 1, але не 2, а електромагнітні поля дають 2, але не 1.
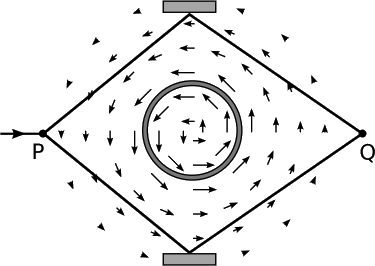
Примітка
Описуємо ефект тут з точки зору ідеалізованого, непрактичного експерименту. Фактичний емпіричний стан ефекту Агаронова-Бома див. Бателаан і Тономура, Фізика сьогодні 62 (2009) 38.
На малюнку 5.9.2 показаний аналог експерименту Агаронова - Бома з диференціальної геометрії. Скрізь, але на кінчику, конус має нульову кривизну, як ми бачимо, вирізаючи його і виклавши рівно. Але навіть спостерігач, який ніколи не відвідує щільно зігнуту область на кінчику, може виявити його існування, тому що паралельно транспортує вектор навколо замкнутого контуру може змінити напрямок вектора за умови, що петля оточує кінчик.
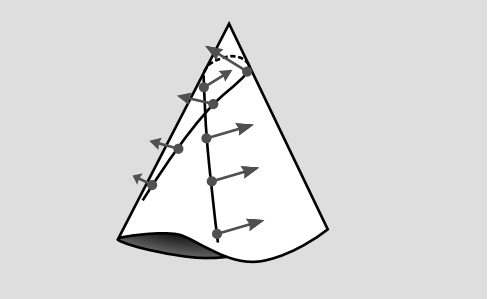
У електромагнітному прикладі інтеграція А навколо замкнутого контуру виявляє за допомогою теореми Стокса існування магнітного потоку через петлю, навіть якщо магнітне поле дорівнює нулю в кожному місці, де потрібно вибірку А. У релятивістському прикладі інтеграція\(\Gamma\) навколо замкнутого циклу показує, що всередині петлі є кривизна, хоча кривизна дорівнює нулю у всіх місцях, де\(\Gamma\) потрібно вибірку.
Той факт, що\(\Gamma\) є вимірювальним полем, а отже, не локально спостережуваним, є просто фантастичним способом вираження ідей, представлених у розділі 5.6, що завдяки принципу еквівалентності гравітаційне поле загалом відносність не є локально спостережуваним. Ця неспостережуваність є локальною, оскільки принцип еквівалентності є твердженням про локальні кадри Лоренца. Приклад на малюнку 5.9.2 є нелокальним.
Приклад 11: Геодезичний ефект і структура джерела
- У розділі 5.5 ми оцінили геодезичний вплив на гравітаційний зонд B і знайшли результат, який був вимкнений лише в 3 рази\(\pi\). Математично чиста форма 3\(\pi\) говорить про те, що геодезичний ефект нечутливий до розподілу маси всередині землі. Чому це повинно бути так?
- Зміна вектора при паралельному транспортуванні його навколо замкнутого контуру може бути виражена через (1) інтеграл площі кривизни всередині петлі або (2) лінійний інтеграл символу Крістоффеля (по суті, гравітаційне поле) на самій петлі. Хоча я висловив оцінку як 1, було б однаково справедливо використовувати 2. За теоремою про оболонку Ньютона, гравітаційне поле не чутливе ні до чого щодо його масового розподілу, крім близької сферичної симетрії. Земля крутиться, і це дійсно впливає на тензор стрес-енергії, але оскільки швидкість, з якою вона обертається, скрізь набагато менше, ніж c, отриманий ефект, званий перетягуванням кадру, набагато менше.
