5.12: Колектори (частина 2)

Визначення локальних координат многовиду

Альтернативним способом характеристики n-многовиду є об'єкт, який локально може бути описаний n дійсними координатами. Тобто будь-яке досить мале сусідство гомеоморфно до відкритої множини в просторі дійсних n-кортежів виду (x ₁, x ₂,., x _n). Наприклад, замкнута напівплощина не є 2-множинним, оскільки жодне сусідство точки на її краю не є гомеоморфним для будь-якого відкритого набору в декартовій площині.

Вправа$\PageIndex{1}$

Самоперевірка: Переконайтеся, що це альтернативне визначення колектора дає ті ж відповіді, що і M1-M3 у всіх наведених вище прикладах.

Грубо кажучи, еквівалентність двох визначень відбувається тому, що ми використовуємо n дійсних чисел як координати для розмірів, зазначених M1, а дійсні числа є унікальною системою числення, яка має звичайні арифметичні операції, впорядковується і є повним у сенсі M3.

Як завжди, коли ми говоримо, що щось «місцеве», виникає питання про те, наскільки місцеве досить місцеве. Мова у визначенні вище про «будь-яке досить маленьке сусідство» логічно схожа на$\epsilon - \delta$ підхід Вейерштрасса: якщо Аліса дає Бобу колектор і точку на колекторі, Боб завжди може знайти деяке сусідство навколо цієї точки, сумісне з координатами, але це може бути надзвичайно невелике сусідство.

Приклад 20: Координати на колі

Якщо ми хочемо визначити координати на колі, вони повинні бути неперервними функціями. Таким чином, кут$\phi$ навколо центру не зовсім працює як глобальна координата, оскільки він має розрив, де$\phi$ = 0 ідентифікується з$\phi = 2 \pi$. Ми можемо обійти це, використовуючи різні координати в різних регіонах, як це гарантовано можливо за допомогою визначення місцевої координати многовиду. Наприклад, ми можемо покрити коло двома відкритими наборами, одним ліворуч і одним праворуч. Лівий, L, визначається видаленням лише точки$\phi$ = 0 з кола. Правильний, R, визначається видаленням лише одного на$\phi = \pi$. На L ми використовуємо координати$0 < \phi_{L} < 2 \pi$, які завжди є неперервною функцією від L до дійсних чисел. На R ми використовуємо$− \pi < \phi_{R} < \pi$.

У таких прикладах, як цей, множини, такі як L і R, називаються патчами. Ми вимагаємо, щоб координатні карти на різних патчах збігалися плавно. У цьому прикладі ми хотіли б, щоб усі чотири наступні функції, відомі як карти переходів, були безперервними:

• $\phi_{L}$як функція$\phi_{R}$ на домені$0 < \phi_{R} < \pi$
• $\phi_{L}$як функція$\phi_{R}$ на домені$− \pi < \phi_{R} < 0$
• $\phi_{R}$як функція$\phi_{L}$ на домені$0 < \phi_{L} < \pi$
• $\phi_{R}$як функція$\phi_{L}$ L на домені$\pi < \phi_{L} < 2 \pi$

Визначення локальної координати лише стверджує, що многовид може бути координатизований. Тобто функції, що визначають координатні карти, не є частиною визначення многовиду, тому, наприклад, якщо двоє людей визначають латки координат на одиничному колі по-різному, вони все одно говорять про точно одному і тому ж многообразі.

Приклад 21: Відкрити гомеоморфний відрізок прямої до прямої

Дозволяти L - відкритий відрізок лінії, наприклад відкритий інтервал (0, 1). L гомеоморфний до рядка, тому що ми можемо зіставити (0, 1) до дійсної лінії через функцію f (x) = tan ($\pi x − \frac{\pi}{2}$).

Приклад 22: Закритий відрізок лінії не гомеоморфний до прямої

Закритий відрізок лінії (який не є різноманіттям) не гомеоморфний до лінії. Якщо ми зіставимо його на лінію, то кінцеві точки повинні перейти до двох спеціальних точок A і B. Тоді немає можливості для відображення відвідати точки екстер'єру до інтервалу [A, B], не відвідуючи A і B більше одного разу.

Приклад 23: Відкритий відрізок лінії не гомеоморфний до внутрішньої частини кола

Якщо внутрішня частина кола може бути відображена гомеоморфізмом f на відкритий відрізок лінії, то розглянемо, що буде, якщо ми взяли замкнуту криву, що лежить всередині кола, і знайшли її зображення. За теоремою проміжного значення f не був би один до одного, але це протиріччя, оскільки f вважалося гомеоморфізмом. Це приклад більш загального факту, що гомеоморфізм зберігає розмірність багатовидів.

Малюнок$\PageIndex{5}$

диференційовані колектори

Диференційований колектор означає різноманіття з достатньою додатковою структурою, щоб ви могли робити обчислення на ньому, але ця додаткова структура не обов'язково включає що-небудь таке фантазійне, як метрика. Як конкретний приклад, припустимо, що в 1 + 1-мірному Галілеєвому всесвіті спостерігач Аліса будує глобальну систему координат (t, x). Її просторовий час явно є різноманіттям, заснованим на визначенні локальних координат, і це вірно, навіть якщо галілеїв простору-час не має метрики. Тим часом спостерігач Боб будує власну систему координат (t', x'). Але щось тривожне відбувається, коли Аліса будує карту переходу від координатної сітки Боба до її. Як показано на малюнку f, сітка Боба має в ній злам. «Боб, - каже Аліса, - щось не так з вашою системою координат. Я припускаю, що в певний час, який ми можемо назвати t = 0, невидимий гігант вдарив ваше тіло невидимим молотком для крокета і раптом змінив ваш стан руху». «Ні в якому разі, Аліса», - відповідає Боб. «Я не відчував, що що-небудь відбувається при t = 0. Я думаю, що ти той, кого вдарили».

Малюнок$\PageIndex{6}$ - «Боб, ваш колектор не гладкий!»

Під диференційованим колектором ми маємо на увазі той, в якому такого роду суперечки ніколи не трапляються. Колектор постачається з набором локальних систем координат, званих діаграмами, і де б ці діаграми не перекривалися, карта переходу диференційована. Кожна координата є диференційованою функцією будь-якої іншої координати. По суті, ми будемо вважати для зручності, що визначено не просто першу похідну, а похідні від усіх ордерів. Це робить наш колектор не просто диференційованим колектором, а плавним колектором. Це визначення звучить залежним від координат, але це не так. Наша колекція діаграм (так звана атласом) може містити нескінченно багато можливих систем координат; ми можемо навіть вказати, що вона містить усі можливі системи координат, які можуть бути отримані одна від одної будь-якою дифеоморфізм.

Дотичний простір

Тепер формалізуємо інтуїтивне поняття дотичного вектора (розділ 3.1), слідуючи за Новиком і Кацем. ¹⁹ Нехай M - це n-мірний гладкий многовид, так що локально він виглядає як евклідовий простір, описуваний дійсними числовими координатами x, y, ..Тепер ми збільшуємо M, щоб сформувати новий топологічний простір, в якому координати можуть включати не тільки дійсні числа, але і числа, які нескінченно відрізняються від реалів, як зазначено в прикладі 3. Відтепер, коли ми говоримо такі речі, як «колектор», ми маємо на увазі цю розширену версію. ²⁰ Виправте деяке нескінченно мале число$\epsilon$ для раз і назавжди та визначте позначення x = O ($\epsilon$), щоб означати, що$\frac{x}{\epsilon}$ це не нескінченно. ²¹

Примітка

Можна визначити інше і більше посилення, зване ^∗ M, яке включало б точки з нескінченно великими координатами. Наприклад, припустимо, що у нас є латка координат з межами координат, які можна записати за допомогою нерівностей, t > 0$\frac{\pi}{4}$, 0$\theta$ ≤ ≤,. Тоді ^∗ M міститиме будь-які скінченні, нескінченно малі та нескінченні значення (t,,.)$\theta$, що задовольняють ці нерівності, і це включало б нескінченні значення t. Ми не будемо робити цього тут, тому що включення ідеалізованих точок на нескінченності є більш корисним у відносності, якщо ми робимо це за допомогою a інший підхід, розглянутий в розділі 7.3.

Примітка

Еквівалентне і явно незалежне від координат визначення полягає в тому, що для кожної гладкої реальної функції в районі точок функція відрізняється в цих точках на величину, яка дорівнює O ($\epsilon$).

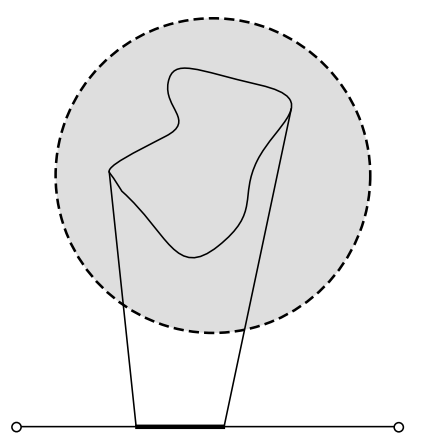
Точки в многовиді вважаються близькими, якщо евклідова відстань між ними в координатному просторі дорівнює O ($\epsilon$). Це визначення звучить залежним від координат, але це не так, і звучить так, ніби це припускає фактичну евклідову метрику, але це не так. ²² Визначте превектор у точці P як пару (P, Q) точок, які близькі, Рисунок 5.10.7 (1). Визначте превектори рівнозначними, якщо різниця між ними нескінченно мала навіть порівняно з$\epsilon$.

Малюнок$\PageIndex{7}$ - 1. Дотичний вектор можна розглядати як нескінченно мале зміщення. Для сфери, вбудованої в трипросторі, простір дотичних векторів візуалізується у вигляді площини, дотичної до сфери в певній точці.

Визначення

Дотичний вектор у точці P - це множина всіх превекторів у P, які еквівалентні певному превектору в P.

Дотичний простір T _P - це сукупність усіх дотичних векторів на P. Дотичний простір має структуру векторного простору над реалами просто за допомогою різниці координат для визначення операцій векторного простору, так само, як ми б робили, якби (P, Q) означало стрілку, що простягається від P до Q, як у першокурсник фізики.

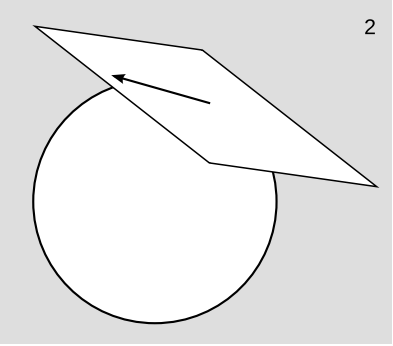
На практиці ми не дуже дбаємо про деталі побудови дотичного простору, і різним людям навіть не доводиться використовувати одну і ту ж конструкцію. Все, що нас хвилює, це те, що дотичний простір має певну структуру. Зокрема, він має n розмірів, як ми очікували інтуїтивно. Оскільки ми збираємося забути деталі конструкції, не має значення, що ми зробили всі дотичні вектори нескінченно малими за визначенням. Внутрішня структура векторного простору пов'язана лише з тим, наскільки великі вектори порівнюються один з одним. (Якби ми хотіли, ми могли б масштабувати всі дотичні вектори в множник$\frac{1}{\epsilon}$.) Це виправдовує візуалізацію на малюнку 5.10.7 (2).

Насправді це не зовсім так, що ми дбаємо лише про внутрішню структуру дотичного простору, тому що тоді ми могли б уникнути химерного визначення і просто використати звичайний векторний простір, що складається з n-кортежів дійсних чисел. Визначення фантазії потрібне, оскільки воно пов'язує дотичний простір природним чином із структурою колектора в певній точці. Тому це дозволить нам (1) визначити паралельний транспорт, який переносить вектор з одного дотичного простору в інший, і (2) визначити компоненти векторів у певній системі координат.

Альтернативне визначення дотичного простору див. Гл. 2 Керролла. ²³ Коротко, це передбачає прийняття дотичного вектора, щоб бути чимось, що поводиться як спрямована похідна. Зокрема, часткова похідна щодо такої координати, як$\frac{\partial}{\partial x}$ кваліфікується як дотичний вектор, який ми вважаємо вказівним у напрямку x. Множина таких координатних похідних утворює основу для дотичного простору і дає зручний спосіб позначення дотичних векторів. Ми знайдемо це позначення зручним в розділі 7.1.

Посилання

¹⁹ «Диференціальна геометрія через нескінченно малі переміщення», arxiv.org/abs/1405.0984

^{23 Конспекти} лекцій з загальної теорії відносності, http://ned.ipac.caltech.edu/level5/March01/Carroll3/Carroll_contents.html.