5.4: Викривлення у двох космічних розмірах

Last updated
Save as PDF

Page ID: 77751

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Оскільки тензори кривизни в розмірах 3+1 складні, почнемо з розгляду більш низьких розмірів. В одному вимірі, рис. 5.3.1, немає такого поняття, як внутрішня кривизна. Це пов'язано з тим, що кривизна описує нездатність паралелізму вести себе як в E5, але поняття паралелізму в одному вимірі немає.

Малюнок$\PageIndex{1}$ - Ця крива не має внутрішньої кривизни.

Найнижчий цікавий вимір, отже, два, і цей випадок вивчав Карл Фрідріх Гаусс на початку дев'ятнадцятого століття. Гаусс провів геодезичну зйомку штату Ганновер, винайшовши оптичний геодезичний прилад під назвою геліотроп, який фактично використовувався для покриття поверхні Землі трикутною сіткою світлових променів. Якщо одна з точок сітки лежить, наприклад, на вершині гори, то сума$\Sigma \theta$ кутів вершин, що зустрічаються в цій точці, буде менше 2$\pi$, суперечить Евкліду. Хоча світлові промені дійсно подорожують по повітрю над брудом, ми можемо думати про них як про наближення до геодезичних робіт, намальованих безпосередньо на бруді, що було б властивим, а не зовнішнім. Кутовий дефект навколо вершини тепер зникає, тому що простір є локально евклідовим, але тепер ми підбираємо інший вид кутового дефекту, який полягає в тому, що внутрішні кути трикутника більше не складаються з евклідовим значенням$\pi$.

Малюнок 5.3.2.png — Малюнок$\PageIndex{2}$ - Геодезист на вершині гори використовує геліотроп.

Малюнок 5.3.3.png — Малюнок$\PageIndex{3}$ - Карта тріангуляційного обстеження, такого як той, який проводив Гаусс. Вимірюючи внутрішні кути трикутників, можна визначити не просто двовимірну проекцію сітки, а її повну тривимірну форму, що включає як кривизну землі (зверніть увагу на кривизну ліній широти), так і висоту об'єктів над і нижче рівня моря.

Приклад 1: Полігональне опитування футбольного м'яча

Малюнок 5.3.3 застосовує подібні ідеї до футбольного м'яча, єдина відмінність полягає у використанні п'ятикутників і шестикутників, а не трикутників.

На малюнку 5.3.4 (1) зйомка є зовнішньою, оскільки лінії проходять нижче поверхні сфери. Кривизна виявляється тому, що кути на кожній вершині складають до 120 + 120 + 110 = 350 градусів, даючи кутовий дефект в 10 градусів.

На малюнку 5.3.4 (2) лінії проектуються для формування дуг великих кіл на поверхні сфери. Оскільки простір є локально евклідовим, сума кутів у вершині має своє евклідове значення 360 градусів. Однак кривизну можна виявити, оскільки сума внутрішніх кутів багатокутника більша за евклідову величину. Наприклад, кожен сферичний шестикутник дає суму 6 × 124,31 градусів, а не евклідова 6 × 120. Кутовий дефект 6 × 4,31 градуса є власною мірою кривизни.

Приклад 2: Кутовий дефект на земній поверхні

Розділіть північну півкулю Землі на чотири октанти, причому їх межі проходять через північний полюс. Ці октанти мають сторони, які є геодезичними, тому вони є рівносторонніми трикутниками. Якщо припустити евклідову геометрію, внутрішні кути рівностороннього трикутника дорівнюють 60 градусам, і, як і будь-який трикутник, вони складають до 180 градусів. Октант-трикутник на малюнку 5.3.5 має кути, які кожен дорівнює 90 градусам, а сума дорівнює 270. Це показує, що поверхня Землі має внутрішню кривизну.

Малюнок 5.3.5.png — Малюнок$\PageIndex{5}$

Цей приклад пропонує інший спосіб вимірювання внутрішньої кривизни, з точки зору відношення$\frac{C}{r}$ окружності кола до його радіусу. У евклідової геометрії це співвідношення дорівнює 2$\pi$. $\rho$Дозволяти радіус Землі, і розглядати екватор як коло з центром на північному полюсі, так що його радіус дорівнює довжині однієї зі сторін трикутника на малюнку 5.3.5,$r = (\frac{\pi}{2}) \rho$. (Не плутайте r, який є власним$\rho$, з, радіус сфери, який є зовнішнім і не дорівнює r.) Тоді співвідношення$\frac{C}{r}$ дорівнює 4, що менше евклідової величини 2$\pi$.

Нехай

\[\epsilon = \sum \theta − \pi\]

бути кутовим дефектом трикутника, а для конкретності нехай трикутник знаходиться в просторі з еліптичною геометрією, так що він має постійну кривизну і може бути змодельований як сфера радіуса$\rho$, з ідентифікованими антиподальними точками.

Вправа$\PageIndex{1}$

В еліптичній геометрії, яке мінімально можливе значення кількості,$\frac{C}{r}$ розглянутої в прикладі 2? Чим це відрізняється від випадку сферичної геометрії?

Ми хочемо, щоб міра кривизни, яка є локальною, але якщо наш простір локально плоский, ми повинні мати,$\epsilon → 0$ як розмір трикутників наближається до нуля. Ось чому евклідова геометрія є хорошим наближенням для маломасштабних карт землі. Дискретна природа трикутної сітки є лише артефактом визначення, тому ми хочемо міру кривизни, яка, на відміну від$\epsilon$, наближається до деякої кінцевої межі, оскільки масштаб трикутників наближається до нуля. Чи варто очікувати, що це масштабування буде йти як$\epsilon \propto \rho$? $\rho^{2}$? Давайте визначимося з масштабуванням. Спочатку доведено класичну лему Гаусса, що стосується дещо іншої версії кутового дефекту, для одного трикутника.

Теорема

В еліптичній геометрії кутовий дефект$\epsilon = \alpha + \beta + \gamma − \pi$ трикутника пропорційний його площі А.

доказ

За аксіомою Е2 продовжити кожну сторону трикутника, щоб утворити лінію, малюнок 5.3.6 (1). Кожна пара ліній перетинає тільки в одній точці (Е1) і ділить площину на дві лінії з їх чотирма вершинами, що торкаються в цій точці, Рисунок 5.3.6 (2). З шести ліній орієнтуємося на три затінені, які перекривають трикутник. У кожному з них два внутрішніх кута у вершині однакові (Евклід I.15). Площа лінії пропорційна її внутрішньому куту, як випливає з розсічення на більш вузькі лінії; оскільки лінія з внутрішнім кутом$\pi$ охоплює всю площу Р площини, константа пропорційності дорівнює$\frac{P}{\pi}$. Сума площ трьох ліній дорівнює$(\frac{P}{\pi})(\alpha + \beta + \gamma)$, але ці три області також охоплюють всю площину, тричі перекриваючись на заданому трикутнику, і тому їх сума також дорівнює$P + 2A$. Прирівнювання двох виразів призводить до бажаного результату.

Малюнок 5.3.6.png — Малюнок$\PageIndex{6}$ - Доказ того, що кутовий дефект трикутника в еліптичній геометрії пропорційний його площі. Кожне біле коло представляє всю еліптичну площину. Пунктирна лінія на краю насправді не є межею; лінії, які відходять від краю, просто обертаються назад. У сферичній моделі білому колу відповідає одна півкуля, яка ототожнюється з протилежним півкулею.

Цей розрахунок був суто внутрішнім, оскільки він не використовував жодної моделі чи координат. Тому ми можемо побудувати міру кривизни, що ми можемо бути впевнені, є власною,$K = \frac{\epsilon}{A}$. Це називається гаусовою кривизною, і в еліптичній геометрії вона постійна, а не змінюється від точки до точки. У моделі на сфері радіуса$\rho$ ми маємо

\[K = \frac{1}{\rho^{2}}.\]

Вправа$\PageIndex{2}$

Самоперевірка: Перевірте рівняння,$K = \frac{1}{\rho^{2}}$ розглянувши трикутник, що охоплює один октант сфери, як у прикладі 2.

Нормальні координати Гаусса

Корисно ввести нормальні або гаусові нормальні координати, визначені наступним чином. Через точку O побудуйте перпендикулярні геодезичні та визначте афінні координати x та y вздовж них. Для будь-якої точки P від осі визначте координати, будуючи лінії через P, які перетинають осі перпендикулярно. Для Р в досить малій околиці О ці лінії існують і однозначно визначаються. Аналогічним чином можна визначити гаусові полярні координати.

Малюнок 5.3.7.png — Малюнок$\PageIndex{7}$ - Гаусові нормальні координати на сфері.

Ось дві корисні тлумачення К.

Гаусова кривизна вимірює провал паралелізму в наступному сенсі. Нехай лінія$\ell$ будується так, щоб вона перетинала нормальну вісь y в (0, dy) під кутом, який відрізняється від перпендикуляра на нескінченно малу величину d$\alpha$ (рис. 5.3.8). Побудувати лінію x' = dx, і нехай d$\alpha'$ буде кут її перпендикулярної форми з$\ell$. Тоді ¹ гаусова кривизна при O дорівнює $$K =\ frac {d^ {2}\ alpha} {dx dy}, $$де$d^{2} \alpha = d \alpha' - d \alpha$.

Малюнок 5.3.8.png — Малюнок$\PageIndex{8}$ - 1. Гаусова кривизна може бути інтерпретована як збій паралелізму, представленого$\frac{d^{2} \alpha}{dx dy}$.

Доказ

Оскільки будь-які дві лінії перетинаються в еліптичній геометрії,$\ell$ перетинає вісь x. Далі слід застосування визначення гаусової кривизни до правильних трикутників, утворених віссю x$\ell$, і лініями при x = 0 і x = dx, так що$K = \frac{d \epsilon}{dA} = \frac{d^{2} \alpha}{dx dy}$, де треті степені нескінченності були відкинуті.

З точки Р випромінюють вентилятор променів під кутами, що заповнюють певний діапазон$\theta$ кутів в гауссових полярних координатах (рис. 5.3.9). Нехай довжина дуги цього вентилятора при r дорівнює L, яка не може дорівнювати його евклідовому значенню L _E = r$\theta$. Потім ² $$K = -3\ розрив {d^ {2}} {dr^ {2}}\ ліворуч (\ dfrac {L} {L_ {E}}\ праворуч)\ ldotp$$

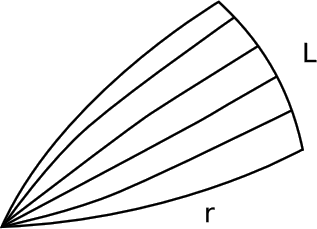
Малюнок 5.3.9.png — Малюнок$\PageIndex{9}$ - *2. Гаусова кривизна як L ≠ r$\theta$.*

Примітка

У сферичній моделі L =$\rho \theta$ sin u, де u - кут, піднесений в центрі сфери дугою довжини r. то маємо$\frac{L}{L_{E}} = \frac{\sin u}{u}$, чия друга похідна по відношенню до u є$- \frac{1}{3}$. Оскільки r =$\rho$ u, друга похідна тієї ж величини по відношенню до r дорівнює$− \frac{1}{3 \rho^{2}} = − \frac{K}{3}$.

Давайте тепер узагальнимо поза еліптичною геометрією. Розглянемо простір, змодельований поверхнею, вбудованою у три виміри, з геодезичними даними, визначеними як криві екстремальної довжини, тобто криві, зроблені шматком струни, натягнутою натягнутою по всій поверхні. У певній точці P ми завжди можемо вибрати систему координат (x, y, z) таким чином, щоб поверхня$z = \frac{1}{2} k_{1} x^{2} + \frac{1}{2} k_{2} y^{2}$ локально наближала поверхню до рівня точності, необхідної для обговорення кривизни. Поверхня або параболоїдна, або гіперболоїдальна (сідло), в залежності від ознак к ₁ і к ₂. Ми могли б наївно думати, що k ₁ і k ₂ можуть бути незалежно визначені за допомогою внутрішніх вимірювань, але, як ми бачили в прикладі 5, циліндр локально не відрізняється від евклідової площини, так що якщо один k дорівнює нулю, інший k явно не може бути визначена. Насправді все, що можна виміряти, - це гаусова кривизна, яка дорівнює добутку k ₁ k ₂. Щоб зрозуміти, чому це має бути правдою, спочатку врахуйте, що будь-яка міра кривизни має одиниці зворотної відстані в квадраті, а k мають одиниці зворотної відстані. Єдиними можливими внутрішніми заходами кривизни на основі k, таким чином, є k ² ₁ +k ^₂ і k ₁ k ₂. (Ми не можемо мати, наприклад, просто k ² ₁, тому що це зміниться під зовнішнім обертанням навколо осі z.) Тільки k ₁ k ₂ зникає на циліндрі, тому це єдина можлива внутрішня кривизна.

Приклад 3: Їдять піцу

Коли люди їдять піцу, складаючи шматочок уздовж, вони користуються власною природою гаусової кривизни. Після того, як k ₁ закріплено на ненульовому значенні, k ₂ не може змінитися без зміни K, тому фрагмент не може впасти.

Приклад 4: еліптична та гіперболічна геометрія

Ми бачили, що фігури, які поводяться відповідно до аксіом еліптичної геометрії, можуть бути змодельовані на частині сфери, яка є поверхнею постійної K> 0. Модель може бути перетворена в глобальну, що задовольняє всім аксіомам, якщо відповідні топологічні властивості забезпечуються шляхом ідентифікації антиподальних точок. Параболоїдна поверхня z = k ₁ x ² + k ₂ y ² може бути хорошим локальним наближенням до сфери, але для точок, далеких від її вершини, K значно змінюється. Еліптична геометрія не має паралелей; всі лінії зустрічаються, якщо протягнуті досить далеко.

Простір постійної негативної кривизни має геометрію, звану гіперболічною, і представляє певний інтерес, оскільки, здається, він описує просторові розміри нашого Всесвіту в космологічному масштабі. Гіперболоїдна поверхня працює локально як модель, але її кривизна лише приблизно постійна; поверхня постійної кривизни - це рогоподібна, створена обертанням гірської кривої, яка називається тратрикс навколо своєї осі. Трактриса обертання не є такою задовільною моделлю, як сфера для еліптичної геометрії, оскільки лінії відрізані на вершині рогу. Гіперболічна геометрія багатша паралелями, ніж евклідова геометрія; з огляду на пряму$\ell$ і точку Р не на$\ell$, через P є нескінченно багато ліній, які не проходять$\ell$.

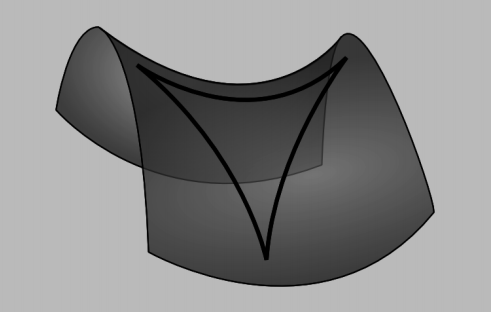
Малюнок 5.3.10.png — Малюнок$\PageIndex{10}$ - Трикутник в просторі з негативною кривизною має кути, які додають менше ніж$\pi$.

Приклад 5: Блоха на футболі

Ми можемо собі уявити, що блоха на поверхні американського футболу може визначити за допомогою внутрішніх локальних вимірювань, в якому напрямку йти, щоб дістатися до найближчого наконечника. Це неможливо, тому що блоха повинна була б визначити вектор, а кривизна не може бути вектором, оскільки$z = \frac{1}{2} k_{1} x^{2} + \frac{1}{2} k_{2} y^{2}$ є інваріантною за інверсією парності x → −x, y → −y. З подібних причин міра кривизни ніколи не може мати непарного рангу.

Не порушуючи симетрію відображення, все ж можна припустити, що блоха могла визначити орієнтацію лінії кінчика до кінчика, що проходить через його положення. Дивно, але навіть це неможливо. Блоха може вимірювати тільки єдине число К, яке не несе ніякої інформації про напрямки в просторі.

5.3.11.пнг — Малюнок$\PageIndex{11}$ - Блоха на футболі не може зорієнтуватися за внутрішніми, місцевими вимірами.

Приклад 6: Громовідвід

Припустимо, у вас є провідник грушоподібної форми, як на малюнку 5.3.12 (1). Так як груша є провідником, то всередині неї всюди є вільні заряди. Панелі 1 і 2 малюнка показують комп'ютерне моделювання зі 100 однаковими електричними зарядами. В 1 заряди звільняються в випадкових положеннях всередині груші. Відштовхування змушує їх усіх вилітати назовні на поверхню, а потім осідати в впорядкований, але нерівномірний малюнок.

Малюнок 5.3.12a.png — Малюнок _5.3.12b.png» />

Малюнок 5.3.12c.png — Малюнок$\PageIndex{12}$ - В 1 і 2 заряди, які видно на лицьовій поверхні провідника, показані у вигляді суцільних точок; інші потрібно було б бачити через провідник, який ми уявляємо напівпрозорим.

Можливо, ми не змогли вгадати шаблон заздалегідь, але ми можемо переконатися, що деякі його особливості мають сенс. Наприклад, зарядка А має більше сусідів праворуч, ніж ліворуч, що, як правило, змушує його прискорюватися вліво. Але коли ми дивимося на картину в цілому, виявляється розумним, що цьому заважає більша кількість більш віддалених зарядів зліва, ніж справа.

Здається, також є закономірність нерівномірності: заряди збираються щільніше в таких областях, як B, де гаусова кривизна велика, і менш щільно в таких областях, як C, де K майже нуль (трохи негативний).

Щоб зрозуміти причину такої закономірності, розглянемо малюнок 5.3.12 (3). Це просто показати, що щільність заряду$\sigma$ на кожній сфері обернено пропорційна її радіусу, або пропорційна K ^1/2. Лорд Кельвін довів, що на провідному еліпсоїді щільність заряду пропорційна відстані від центру до дотичної площини, що еквівалентно ³$\sigma \propto$ К ^1/4; цей результат виглядає схожим за винятком різного показника. МакАллістер показав у 1990 році ⁴, що ця поведінка K ^1/4 застосовується до певного класу прикладів, але вона явно не може застосовуватися у всіх випадках, оскільки, наприклад, K може бути негативним, або ми можемо мати глибоку увігнутість, яка б утворила клітку Фарадея. Завдання 1 обговорює випадок ножа-кромки.

Подібні міркування показують, чому Бенджамін Франклін використовував гострий наконечник, коли винайшов громовідвід. Заряджені грозові хмари спонукають позитивні та негативні заряди рухатися до протилежних кінців стрижня. На загостреному верхньому кінці стрижня заряд прагне сконцентруватися в точці, і цей заряд притягує блискавку. Такий же ефект іноді можна помітити, коли клаптик алюмінієвої фольги ненароком кладуть в мікрохвильовку. Сучасні експерименти ⁵ показують, що хоча гострий кінчик найкраще підходить при запуску іскри, більш помірна крива, як і правий кінчик груші в даному прикладі, краще успішно витримує іскру досить довго, щоб підключити розряд до хмар.

³ http://math.stackexchange.com/questi...f-the-distance

4 Я W Макаллістер 1990 р. Фіз. D: Яблуко. Фіз 23 359

⁵ Мур та співавт., Журнал прикладної метеорології 39 (1999) 593