5.11: Колектори (частина 1)

Цей розділ можна опустити при першому читанні.

Навіщо нам потрібні колектори

Загальна відносність не передбачає заздалегідь визначеної фонової метрики, і це створює проблему курки та яєць. Ми хочемо визначити метрику на деякому просторі, але як ми навіть вказати набір точок, які складають цей простір? Звичайний спосіб визначення набору точок буде за їх координатами. Наприклад, у двох вимірах ми могли б визначити простір як набір усіх впорядкованих пар дійсних чисел (x, y). Але це не працює в загальній теорії відносності, тому що простір не гарантовано матиме цю структуру. Наприклад, в класичній комп'ютерній грі 1979 року «Астероїди» космос «обгортається», так що якщо ваш космічний корабель злетить з правого краю екрану, то він знову з'являється зліва, і аналогічно вгорі і внизу (рис.$\PageIndex{1}$).

Малюнок$\PageIndex{1}$: В астероїдах простір «обгортається».

Ще до того, як ми накладемо метрику на цей простір, він має топологічні властивості, які відрізняються від властивостей евклідової площини. Під «топологічними» ми маємо на увазі властивості, які зберігаються, якщо простір розглядається як лист гуми, який можна розтягнути будь-яким способом, але не зрізати або склеїти назад. Топологічно простір в астероїдах еквівалентний тору (поверхні пончика), але не евклідовій площині.

Малюнок$\PageIndex{2}$: Кавова чашка топологічно еквівалентна тору.

Ще один корисний приклад - поверхня сфери. У прикладі 10 ми розрахували$\Gamma^{\theta}_{\phi \phi}$. Подібний розрахунок дає$\Gamma^{\theta}_{\phi \phi} = \cot \frac{\theta}{R}$. Тепер розглянемо, що відбувається, коли ми їдемо наших собачоїупряжках на північ уздовж лінії довготи$\phi$ = 0, перетинаємо північний полюс при$\theta$ = 0, і продовжуємо по тій же геодезичній. Коли ми перетинаємо полюс, наша довгота різко змінюється від 0 до$\pi$. Звертаючись до геодезичного рівняння, ми бачимо, що це відбувається тому, що$\Gamma^{\theta}_{\phi \phi}$ вибухає при$\theta$ = 0. Звичайно, нічого особливого не відбувається на полюсі. Погана поведінка - це не вина сфери, це вина вибраних нами$(\theta, \phi)$ координат, які трапляються погано поводяться на полюсі. На жаль, неможливо визначити пару координат на два-сфері, не маючи їх десь поганого поводження. (Це випливає зі знаменитої теореми Брауера 1912 року «Волохаті кулі», в якій стверджується, що неможливо розчісувати волосся на сфері, не створивши десь ковлик.)

Топологічне визначення різноманіття

Це мотивує нас спробувати визначити геометричний простір «голих кісток», в якому немає заздалегідь визначеної метрики або навіть будь-якого заздалегідь визначеного набору координат.

Існує загальне поняття топологічного простору, яке є занадто загальним для наших цілей. У такому просторі єдина структура, яку ми гарантуємо, полягає в тому, що певні множини визначаються як «відкриті», в тому ж сенсі, що інтервал, подібний 0 < x < 1, називається «відкритим». Точку у відкритому наборі можна переміщати в будь-якому напрямку, не виходячи з набору. Відкрита множина - це, по суті, множина без кордону, бо в множині, як 0 ≤ x ≤ 1, граничні точки 0 і 1 можна переміщати лише в одному напрямку, не виводячи їх назовні.

Рисунок$\PageIndex{3}$: Загальна теорія відносності не передбачає визначеної фонової метрики. Тому все, що ми можемо дійсно знати, перш ніж ми обчислюємо що-небудь, це те, що ми працюємо над колектором, без метрики, накладеної на нього.

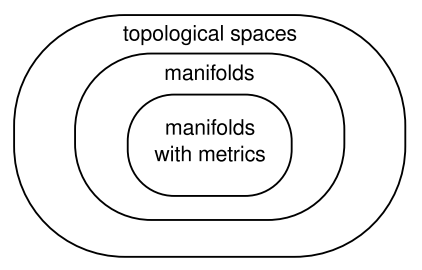
Топологічний простір для нас занадто загальний, оскільки він може включати такі простори, як фрактали, нескінченновимірні простори та простори, які мають різну кількість вимірів у різних регіонах. Проте корисно розпізнавати певні поняття, які можна визначити, використовуючи лише загальний апарат топологічного простору, щоб ми знали, що вони жодним чином не залежать від наявності метрики. Відкритий набір, що оточує точку, називається околицею цієї точки. У топологічному просторі ми маємо поняття отримання довільно близько до певної точки, що означає приймати менші та менші квартали, кожен з яких є підмножиною останнього. Але оскільки метрики немає, ми не маємо жодної концепції порівняння відстаней віддалених точок, наприклад, що P ближче до Q, ніж R до S. Неперервна функція є чисто топологічною ідеєю; безперервна функція є такою, що для будь-якого відкритого підмножини U його діапазону, множина V точок у своїй області, які є зіставлений на точки в U також відкритий. Хоча деякі визначення неперервних функцій говорять про дійсні числа$\delta$, як$\epsilon$ і, поняття безперервності не залежить від існування будь-якої структури, такої як дійсна система числення. Гомеоморфізм - це функція, яка є оборотною і безперервною в обох напрямках. Гомеоморфізми формалізують неформальне поняття «гумово-листова геометрія без різання або склеювання». Якщо гомеоморфізм існує між двома топологічними просторами, ми говоримо, що вони гомеоморфні; вони мають однакову структуру і в деякому сенсі є одним і тим же простором.

Більш конкретний тип топологічного простору, який ми хочемо, називається різноманіттям. Не намагаючись будь-якого високого рівня математичної строгості, ми визначаємо n-мірний многовид M відповідно до таких неформальних принципів: ¹⁶

Примітка

Для тих, хто знає топологію, вони можуть бути формалізовані трохи більше: ми хочемо повністю нормальний, другий лічильник, локально пов'язаний топологічний простір, який має Лебега, що охоплює розмірність n, є однорідним простором під власною групою гомеоморфізму і є повним рівномірним простором. Я не знаю, чи достатньо цього, щоб повністю охарактеризувати колектор, але досить виключити всі контрприклади, про які я знаю.

• M1 вимір: вимір М є п.
• М2 Однорідність: Жодна точка не має жодної локально визначеної властивості, яка відрізняє її від будь-якої іншої точки.
• M3 Повнота: M є повним, у тому сенсі, що вказівка довільно невеликої околиці дає унікальне визначення точки.

Приклад 12: Лінії

Безліч всіх дійсних чисел - це 1-множник. Аналогічно, будь-який рядок з властивостями, зазначеними в Elements Евкліда, є 1-маніфольдом. Всі такі лінії гомеоморфні один до одного, і тому ми можемо говорити про «лінію».

Приклад 13: коло

Коло (не включаючи його внутрішню частину) - це 1-колектор, і він не гомеоморфний до лінії. Щоб побачити це, зверніть увагу, що видалення точки з кола залишає її в одному з'єднаному фрагменті, але видалення точки з лінії робить дві. Тут ми використовуємо той факт, що гомеоморфізм гарантовано зберігає властивості «гумово-листового» типу кількості штук.

Приклад 14: Без змін розмірності

«Льодяник», утворений приклеюванням відкритого 2-го кола (тобто кола, що не включає його межу) до відкритого відрізку лінії, не є многообразием, тому що немає n, для якого він задовольняє M1.

Це також порушує М2, оскільки точки в цьому наборі потрапляють на три різні класи: класи, які живуть у двовимірних кварталах, ті, що живуть в 1-мірних кварталах, і точка, де відрізок лінії перетинає межу кола.

Приклад 15: Немає многовидів, зроблених з раціональних чисел

Раціональні числа не є множиною, тому що вказівка довільно малого сусідства навколо$\sqrt{2}$ виключає кожне раціональне число, порушуючи M3.

Аналогічно, раціональна площина, визначена раціонально-числовими парами координат (x, y), не є двократним. Добре, що ми виключили цей простір, тому що він має нефізичну властивість, яку криві можуть перетинати, не маючи спільної точки. Наприклад, крива y = x ² перетинається з одного боку лінії y = 2 на іншу, але ніколи не перетинає її. Це фізично небажано, тому що це не збігається з тим, що ми маємо на увазі, коли ми говоримо про зіткнення між частинками як перетину їхніх світових ліній, або коли ми говоримо, що лінії електричного поля не повинні перетинатися.

Приклад 16: немає кордону

Відкрита напівплощина y > 0 у декартовій площині є 2-множником. Закрита напівплощина y ≥ 0 не є, оскільки вона порушує M2; граничні точки мають інші властивості, ніж ті, що знаходяться на внутрішній.

Приклад 17: Відключені колектори

Дві непересічні лінії - це 1-колектор. Фізично роз'єднані многовиди такого типу представляли б всесвіт, в якому спостерігач в одному регіоні ніколи не зміг би дізнатися про існування іншого регіону.

Приклад 18: Немає поганих завдань з клею

Тримайте руки, як ви робите вигляд, що знаєте карате, а потім використовуйте одну руку, щоб карате-рубати іншу. Припустимо, ми хочемо об'єднати дві відкриті півплощини таким чином. Поки вони окремі, то у нас є цілком законний відключений колектор. Але якщо ми хочемо з'єднати їх, додавши точку Р, де їх межі збігаються, то порушуємо М2, тому що ця точка має особливі властивості, якими не володіють ніякі інші. Прикладом такої властивості є те, що існують точки Q і R такі, що кожна безперервна крива, що з'єднує їх, проходить через P. (Cf. завдання 5)

Хаусдорф власність

Піонерський тополог Фелікс Хаусдорф визначив таку властивість топологічного простору.

Визначення: Hausdorff власність

З огляду на будь-які два пункти, можна знайти незв'язані з ними околиці.

Жарт/мнемоніка, яка, мабуть, найкраще працює для людей з певним типом британського акценту, полягає в тому, що в просторі Хаусдорфа будь-які дві точки можуть бути «розміщені» одна від одної всередині власних непересічних відкритих наборів. Поняття сильно апелює до наших інтуїтивних уявлень про те, як поводяться простір і час, і стандартне визначення різноманіття означає, що це Хаусдорф. Коли ми моделюємо простір Мінковського за допомогою координат реального числа, це Hausdorff. Оскільки принцип еквівалентності говорить, що просторовийчас локально Мінковський, можна також сказати, що це означає, що простор-час - це Хаусдорф. Однак загальна відносність дозволяє просторучасу погано вести себе у таких випадках, як особливості, тому можна уявити, що наш Всесвіт містить точки, які порушують властивість Хаусдорфа. Існують цікаві та фізично вмотивовані просторичаси, такі як деякі версії простору Тауб-горіха, які не є Хаусдорффом. Оскільки у нас немає емпіричних даних про поведінку простору-часу в самих екстремальних умовах, ми не можемо сказати, чи дійсно простор-час є Хаусдорфом. Слід зберігати певний скептицизм щодо того, чи є така ідеалізована категорія навіть значущою в науці, оскільки вона відноситься до явищ у довільно малих масштабах, тоді як теорії та вимірювання обмежені в масштабах, з якими вони можуть мати справу. Гарне обговорення властивості Хаусдорфа, що застосовується до відносності, дає Ерман. ¹⁷

Приклад 19: Розгалуження всесвітів

$\PageIndex{4}$На малюнку показані просторово-часові діаграми 1 + 1-вимірних всесвітів, які розгалужуються як дерево. Це зображення класичної загальної теорії відносності, хоча одна з найсильніших мотивацій для розгляду таких можливостей походить від спроб побудувати теорію квантової гравітації. У таких теоріях зазвичай очікується, що просторовийчас матиме структуру в масштабі Планка, яка є своєрідною «квантовою піною».

Малюнок$\PageIndex{4}$: S діаграми темпу 1 + 1-вимірних всесвітів.

Приклад на малюнку$\PageIndex{4A}$ - це різноманіття, і є Хаусдорфом. Це приклад зміни топології, що означає, що просторовий розділ в один час має іншу топологію, ніж розділ в іншому. ¹⁸ Хоча таке розгалуження може відбуватися без існування будь-яких особливостей, теореми Тіплера та Героха показують, що повинні відбуватися інші типи неправильної поведінки, включаючи порушення причинно-наслідкового зв'язку та необхідність форм матерії, що порушують енергетичні умови.

$\PageIndex{4B}$Малюнок якісно відрізняється. Тут ми сформували простор часу, склеївши між собою три штуки. Ніякої кривизни не мається на увазі; це можуть бути три частини простору Мінковського. Простір-час не є різноманіттям, оскільки точки на з'єднанні мають різні локальні властивості, ніж точки в іншому місці. Механізм загальної відносності руйнується в такому випадку, але, наприклад, ми могли б уявити, що геодезичний в цьому просторічасі може розщедритися на дві різні геодезичні системи після розколу.

Ще третя можливість полягає в тому, щоб переосмислити малюнок$\PageIndex{4B}$ таким чином, щоб було дві різні копії шва. Наприклад, ми могли б дозволити частину діаграми, що поширюється в минуле, бути представлена точками з t < 0, тоді як дві гілки, що продовжуються в майбутнє, можуть мати t ≥ 0, так що для даного x ми мали б дві різні події з координатами (t = 0, x). Неможливо було б поставити ці дві точки в неспільних кварталах, тому ця версія простору не є Хаусдорффом.

---

¹⁸ Щодо недавнього лікування див. Борде, 1994, «Зміна топології класичної загальної теорії відносності», arxiv.org/abs/gr-qc/9406053.

Посилання

¹⁷ Джон Ерман, «Обрізка деяких гілок з «розгалуження космічних часів», «Pitt.edu/~ Jearman/earman2008a.pdf