5.9: Торсіон

У цьому розділі описано поняття гравітаційного кручення. Його можна пропустити без втрати безперервності, за умови, що ви приймаєте властивість симетрії,\(\Gamma^{a}_{[bc]} = 0\) не турбуючись про те, що це означає фізично або які емпіричні докази це підтверджують.

Вправа\(\PageIndex{1}\)

Самоперевірка: інтерпретуйте математичне значення рівняння\(\Gamma^{a}_{[bc]} = 0\), яке виражається в введеному раніше позначенні.

Чи залежать від шляху скалярів?

Здається зрозумілим, що щось на кшталт коваріантної похідної потрібне для векторів, оскільки вони мають напрямок у просторово-часі, і, таким чином, їх заходи змінюються, коли змінюється сама міра простору-часу. Оскільки скаляри не мають напряму в просторовічасі, до них не поширюються ті самі міркування, і це відображено в наших правилах щодо коваріантних похідних. Коваріантна похідна має один\(\Gamma\) термін для кожного індексу диференційованого тензора, тому для скаляра взагалі не повинно бути\(\Gamma\) термінів, тобто\(\nabla_{a}\) таке ж, як\(\partial_{a}\).

Але тільки тому, що похідні скалярів не потребують спеціального лікування з цієї конкретної причини, це не означає, що вони гарантовано поводяться так, як ми інтуїтивно очікуємо, в дивному світі координатно-інваріантної відносності.

Одним з можливих способів для скалярів поводитися контрінтуїтивно було б за аналогією з паралельним транспортом векторів. Якщо ми встромляємо вектор у коробку (як, наприклад, гіроскопи на борту Gravity Probe B) і проведемо його навколо замкнутого контуру, він змінюється. Чи може те ж саме статися зі скаляром? Це вкрай неінтуїтивно, оскільки немає підстав уявляти собі такий ефект в жодній з моделей, які ми побудували з криволінійних просторів. Насправді це не просто контрінтуїтивно, а математично неможливо, згідно з наступним аргументом. Єдина причина, по якій ми можемо інтерпретувати ефект вектора в коробці як випливає з геометрії простору-часу, полягає в тому, що він однаково застосовується до всіх векторів. Якби, наприклад, він застосовувався лише до векторів магнітної поляризації феромагнітних речовин, то ми б інтерпретували його як магнітне поле, що живе в простору-часі, а не властивість самого простору-часу. Якби значення скаляра в коробці було залежним від шляху, і ця залежність від шляху була геометричною властивістю просторучасу, то вона повинна була б застосовуватися до всіх скалярів, включаючи, скажімо, маси і заряди частинок. Таким чином, якщо маса електрона збільшилася на 1% при транспортуванні в коробці по певному шляху, його заряд також повинен збільшитися на 1%. Але тоді його відношення заряду до маси залишилося б інваріантним, і це протиріччя, оскільки відношення заряду до маси також є скалярним, і повинно було відчути той самий 1% ефект. Оскільки різна ідея скаляра-в-коробці призводить до протиріччя, не випадково ми не змогли знайти модель, яка спричинила такий ефект; теорія, якій не вистачає самоузгодженості, не має жодних моделей.

Вправа\(\PageIndex{2}\)

Самоперевірка: Поясніть, чому паралельне транспортування вектора може лише обертати його, а не змінювати його величину.

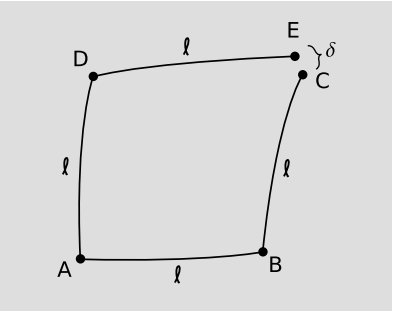
Існує, однак, інший спосіб, яким скаляри могли поводитися контрінтуїтивно, і цей математично самопослідовний. Припустимо, що Хелен живе в двох просторових вимірах і володіє термометром. Вона хоче виміряти просторові зміни температури, зокрема її змішану другу похідну\(\frac{\partial^{2} T}{\partial x \partial y}\). Вдома вранці в точці А вона готується, калібруючи свій гірокомпас до точки на північ і вимірюючи температуру. Потім вона їде\(\ell\) = 1 км на схід уздовж геодезичної до B, консультується зі своїм гірокомпасом і повертає на північ. Вона продовжує один кілометр на північ до С, проби зміни температури\(\Delta T_{1}\) щодо свого будинку, а потім відстежує свої кроки, щоб повернутися додому на обід. У другій половині дня вона перевіряє свою роботу, проводячи той самий процес, але цього разу вона міняє ролі півночі та сходу, подорожуючи вздовж ADE. Якби вона жила в плоскому просторі, це сформувало б дві інші сторони квадрата, а її зразок температури вдень знаходився\(\Delta T_{2}\) б у тій же точці простору C, що і її ранковий зразок. Вона насправді не розпізнає ландшафт, тому вибіркові точки C і E різні, але це лише підтверджує те, що вона вже знала: простір не плоский. ¹⁰

Малюнок\(\PageIndex{1}\) - Вимірювання\(\frac{\partial^{2} T}{\partial x \partial y}\) для скаляра Т.

Малюнок\(\PageIndex{2}\) - Гіроскопи обидва обертаються при транспортуванні з А в Б, змушуючи Олену орієнтуватися по БК, який не утворює прямого кута з АВ. Кут між двома осями гіроскопів завжди однаковий, тому обертання не можна спостерігати локально, але це створює спостережуваний зазор між C та E.

Примітка

Цей момент був згаданий в розділі 5.4, в зв'язку з визначенням тензора Рімана.

Нічого з цього поки не здається дивним, але зараз є два якісно різних способу, якими міг би вийти її аналіз її даних, вказуючи на якісно різні речі про закони фізики в її Всесвіті. Визначення похідної як межі вимагає, щоб вона повторювала експеримент в менших масштабах. Як\(\ell\) → 0, результат для\(\frac{\partial^{2} T}{\partial x \partial y}\) повинен наближатися до певної межі, а похибка повинна зменшуватися пропорційно\(\ell\). Зокрема, різниця між результатами, виведеними з\(\Delta T_{1}\) і\(\Delta T_{2}\) вказують на помилку, і невідповідність між другими похідними, виведеними з них, повинна зменшуватися відповідним чином у міру\(\ell\) скорочення. Припустимо, цього не відбувається. Оскільки часткові похідні комутують, робимо висновок, що процедура її вимірювання не є такою ж, як часткова похідна. Назвемо її процедурою вимірювання\(\nabla\), щоб вона спостерігала невідповідність між\(\nabla_{x} \nabla_{y}\) і\(\nabla_{y} \nabla_{x}\). Той факт, що комутатор\(\nabla_{x} \nabla_{y} − \nabla_{y} \nabla_{x}\) не зникає, не може бути пояснений символами Крістоффеля, тому що те, що вона диференціює, є скалярним. Оскільки невідповідність виникає повністю через нездатність належним чином\(\Delta T_{1} − \Delta T_{2}\) зменшити масштаб, висновок полягає в тому, що відстань\(\delta\) між двома точками вибірки не зменшується так швидко, як ми очікуємо. У наших знайомих моделям двовимірних просторів як поверхонь, вбудованих в трипросторі, ми завжди маємо\(\delta \sim \ell^{3}\) для малих\(\ell\), але вона виявила, що вона лише стискається так само швидко, як\(\ell^{2}\).

Для підказки про те, що відбувається, зверніть увагу, що комутатор\(\nabla_{x} \nabla_{y} − \nabla_{y} \nabla_{x}\) має особливу передачу до нього. Наприклад, він перевертає свій знак під відображенням через лінію y = x. коли ми «паралельні» -транспортні вектори, вони насправді не залишаються паралельними. У цій гіпотетичній всесвіті вектор в коробці, що транспортується на невелику відстань,\(\ell\) обертається на кут, пропорційний\(\ell\). Цей ефект називається крутіння. Хоча жоден ефект кручення не проявляється в наших знайомих моделям, це не тому, що крутіння не вистачає самоузгодженості. Моделі просторів з крутіння дійсно існують. Зокрема, ми бачимо, що крутіння не призводить до такого ж логічного протиріччя, як ідея змінного скаляра-в-коробці. Оскільки всі вектори крутяться на однакову кількість при транспортуванні, внутрішні продукти зберігаються, тому неможливо поставити два вектори в одну коробку і отримати парадокс скаляра-в-коробці, спостерігаючи за зміною їх внутрішнього продукту при транспортуванні коробки.

Зверніть увагу, що лікті ABC і ADE не мають прямих кутів. Якби Олена принесла з собою пару гірокомпасів, один для x і один для y, вона б виявила, що прямий кут між гірокомпасами зберігся при паралельному транспорті, але що гірокомпас спочатку дотичний до геодезичного не залишився таким. Є насправді два нерівнозначних визначення геодезичного в просторі з крутіння. Найкоротший шлях між двома точками не обов'язково збігається з найпрямішим можливим шляхом, тобто той, який паралельно переносить власний тангенсний вектор.

Тензор кручення

Так як кручення непарне при парності, він повинен бути представлений тензором непарного рангу, який ми називаємо\(\tau^{c}_{ab}\) і визначаємо відповідно

\[(\nabla_{a} \nabla_{b} - \nabla_{b} \nabla_{a})f = - \tau^{c}_{ab} \nabla_{c} f,\]

де f - будь-яке скалярне поле, наприклад температура в попередньому розділі. Існує два різних способи, за допомогою яких простір може бути неевклідовим: він може мати кривизну, або він може мати кручення. Для повного обговорення того, як поводитися з математикою простору-часу як з кривизною, так і крученням, див. Статтю Стюарда Дженсена за адресою http://www.slimy.com/~steuard/teaching/tutorials/GRtorsion.pdf. Для наших теперішніх цілей головним математичним фактом, який варто відзначити, є те, що зникаюче крутіння еквівалентно\(\Gamma^{a}_{bc} = \Gamma^{a}_{cb}\) симетрії символів Крістоффеля. Використовуючи позначення, введені раніше,\(\Gamma^{a}_{[bc]} = 0\) якщо\(\tau = 0\).

Вправа\(\PageIndex{3}\)

Самоперевірка: Використовуйте аргумент, подібний до того, який у прикладі 5, щоб довести, що жодна модель двох просторів, вбудованих у три простору, не може мати кручення.

Узагальнюючи до більшої кількості вимірів, тензор кручення непарний при відображенні повного простору x _{a → −x a}, тобто інверсія парності плюс часовий розворот, PT.

У наведеній вище історії ми мали кручення, яке не зберігало дотичні вектори. Однак у трьох або більше вимірах можна мати кручення, яке зберігає дотичні вектори. Наприклад, транспортування вектора вздовж осі x може спричинити лише обертання в площині y-z. Це стосується симетрії тензора кручення, який для зручності ми запишемо в системі координат x-y-z і в повністю коваріантному вигляді\(\tau_{\lambda \mu \nu}\). Визначення тензора кручення має на увазі\(\tau_{\lambda (\mu \nu)} = 0\), тобто, що тензор кручення є антисиметричним за своїми двома кінцевими показниками. Торсіон, який не зберігає дотичні вектори, матиме незникаючі елементи, такі як\(\tau_{xxy}\), що означає, що паралельний транспортування вектора вздовж осі x може змінити його компонент x. Торсіон, який зберігає дотичні вектори, буде\(\tau_{\lambda \mu \nu}\) зникати\(\lambda, \mu\), якщо вони не будуть різними.\(\nu\) Це приклад типу антисиметрії, знайомий з векторного перехресного добутку, в якому перехресні добутки базисних векторів ведуть себе як x × y = z, y × z = x, y × z = x . Узагальнюючи позначення для симетризації та антисиметризації тензорів з ранніх, ми маємо

\[\begin{align} T_{(abc)} &= \frac{1}{3!} \Sigma T_{abc} \\ T_{[abc]} &= \frac{1}{3!} \Sigma \epsilon^{abc} T_{abc}, \end{align}\]

де суми знаходяться над усіма перестановками індексів, а у другому рядку ми використали символ Леві-Чівіта. У цьому позначенні абсолютно антисиметричний тензор кручення є одним з\(\tau_{\lambda \mu \nu} = \tau_{[\lambda \mu \nu]}\), а кручення цього типу зберігає тангенсні вектори при перекладі.

Малюнок\(\PageIndex{3}\) - Три гіроскопа спочатку вирівняні з осями x, y і z. Після паралельного транспортування уздовж геодезичної осі x гіроскоп x все ще вирівняний з віссю x, але гіроскопи y та z оберталися.

У двох вимірах немає абсолютно антисиметричних об'єктів з трьома індексами, тому що ми не можемо записати три індекси, не повторюючи один. У трьох вимірах антисиметричний об'єкт з трьома індексами просто кратний тензору Леві-Чівіта, тому абсолютно антисиметричне кручення, якщо воно існує, представлено одним числом; при перекладі вектори обертаються як правосторонні, так і лівосторонні гвинти, і це число говорить нам про швидкість обертання. У чотирьох вимірах ми маємо чотири незалежно змінні величини\(\tau_{xyz}, \tau_{tyz}, \tau_{txz}\), і\(\tau_{txy}\). Іншими словами, антисиметричне кручення 3+1 просторучасу може бути представлено чотирьохвектором,\(\tau^{a} = \epsilon^{abcd} \tau_{bcd}\).

Експериментальні пошуки кручення

Один із способів встановлення принципу еквівалентності (див. Розділ 4.4) полягає в тому, що він забороняє простору-час надходити обладнаним векторним полем, яке може бути виміряно вільно падаючими спостерігачами, тобто спостерігачами в місцевих кадрах Лоренца. Проведено різноманітні високоточні випробування принципу еквівалентності. З точки зору експериментатора, який проводить подібний вид тесту, важливо розрізняти поля, які «вбудовані» до простору-часу, і ті, що живуть у простору-часі. Наприклад, існування магнітного поля землі не порушує принципу еквівалентності, але якби експеримент був чутливий до земного поля, а експериментатор про це не знав, то виявилося б порушення. Антисиметричне кручення в чотирьох вимірах діє подібно вектору. Якщо він являє собою універсальний фоновий ефект, вбудований в просторучас, то він порушує принцип еквівалентності. Якщо він натомість виникає з конкретних матеріальних джерел, то він все ще може проявлятися як вимірюваний ефект в експериментальних тестах, призначених для виявлення інваріантності Лоренца. Розглянемо останню можливість.

Оскільки кривизна в загальній теорії відносності походить від маси та енергії, представленої тензором стрес-енергії T _ab, ми могли б запитати, якими були б джерела кручення, якщо воно існує в нашому Всесвіті. Джерелом не може бути тензор енергії стресу 2 рангу. Це повинен бути тензор непарного рангу, тобто величина, яка є непарною під PT, і в теоріях, що включають кручення, прийнято вважати, що джерелом є квантово-механічний кутовий імпульс субатомних частинок. Якщо це так, то очікується, що ефекти кручення будуть пропорційними\(\hbar\) G, добутку постійної Планка і гравітаційної постійної, і тому вони повинні бути надзвичайно малими і важко виміряти. Теорія струн, наприклад, включає кручення, але ніхто не знайшов способу перевірити теорію струн емпіричним шляхом, оскільки вона по суті робить прогнози про явища за шкалою Планка,\(\sqrt{\frac{\hbar G}{c^{3}}}\) 10 ⁻³⁵ м, де гравітація і квантова механіка є сильними ефектами.

Однак існують деякі високоточні експерименти, які мають розумний шанс виявити, чи є у нашого Всесвіту кручення. Торсіон порушує принцип еквівалентності, і до кінця століття випробування принципу еквівалентності досягли рівня точності, достатнього, щоб виключити деякі моделі, що включають кручення. На малюнку 5.8.4 показаний торсіонний маятник, який використовується в експерименті групою Eöt-Wash у Вашингтонському університеті. ¹¹ Якщо крутіння існує, то внутрішній\(\boldsymbol{\sigma}\) спін електрона повинен мати енергію\(\boldsymbol{\sigma} \cdot \boldsymbol{\tau}\), де\(\boldsymbol{\tau}\) знаходиться космічна частина торсіонного вектора. Кручення може генеруватися землею, сонцем або будь-яким іншим об'єктом на більшій відстані. Взаємодія\(\boldsymbol{\sigma} \cdot \boldsymbol{\tau}\) змінить поведінку торсіонного маятника, якщо спини електронів у маятнику поляризовані невипадково, як у магнітному матеріалі. Маятник буде мати тенденцію до прецесії навколо осі, визначеної\(\boldsymbol{\tau}\).

Малюнок\(\PageIndex{4}\) - Торсіонний маятник Вашингтонського університету використовується для пошуку кручення. Світло-сірі клини - Alnico, темніші SmCo5. Стрілки з заповненими головками зображують напрямки обертань електронів, при цьому більш щільні стрілки вказують на більш високу поляризацію. Стрілки з відкритими головками показують напрямок поля B.

Цей тип експерименту є надзвичайно складним, оскільки маятник має тенденцію діяти як надчутливий магнітний компас, в результаті чого вимірюється навколишнє магнітне поле, а не гіпотетичне торсіонне поле\(\boldsymbol{\tau}\). Щоб усунути це джерело систематичної похибки, група UW спочатку максимально добре усунула навколишнє магнітне поле, використовуючи mu-металеве екранування та котушки Гельмгольца. Вони також сконструювали маятник з комбінації двох магнітних матеріалів, Alnico 5 і SmCo ₅, таким чином, що магнітний дипольний момент зник, але спіновий дипольний момент не зробив; Магнітне поле Alnico 5 майже повністю пов'язано з електронним спіном, тоді як магнітне поле SmCo ₅ містить значний внесок від орбітального руху. В результаті вийшов немагнітний об'єкт, спини якого поляризувалися. Після чотирьох років збору даних вони виявили\(|\boldsymbol{\tau}| \lesssim 10^{−21}\) eV. Моделі, що включають кручення, зазвичай прогнозують, що такі ефекти мають порядок\(\frac{m^{2}_{e}}{m_{P}} ∼ 10^{−17}\) еВ, де m _e - маса електрона, а\(m_{P} = \sqrt{\frac{\hbar c}{G}}\) ≈ 10 ¹⁹ ГеВ ≈ 20\(\mu\) г - маса Планка. Тому широкий клас цих моделей виключається цими експериментами.

Оскільки, здається, немає експериментальних доказів існування гравітаційного кручення у нашому Всесвіті, ми будемо вважати, що відтепер він зникає однаково. Ейнштейн зробив те ж припущення, коли спочатку створив загальну відносність, хоча пізніше він і Картан возитися з теоріями без кручення в невдалій спробі об'єднати гравітацію з електромагнетизмом. Деякі моделі, що включають кручення, залишаються життєздатними. Наприклад, стверджувалося, що тензор кручення повинен швидко відвалюватися з відстані від джерела. ¹²

Посилання

¹¹ http://arxiv.org/abs/hep-ph/0606218

¹² Керролл і Філд, http://arxiv.org/abs/gr-qc/9403058