Skip to main content
LibreTexts - Ukrayinska

5: Молекулярні орбіталі

  1. Last updated
  2. Save as PDF
  • Page ID
    32761

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

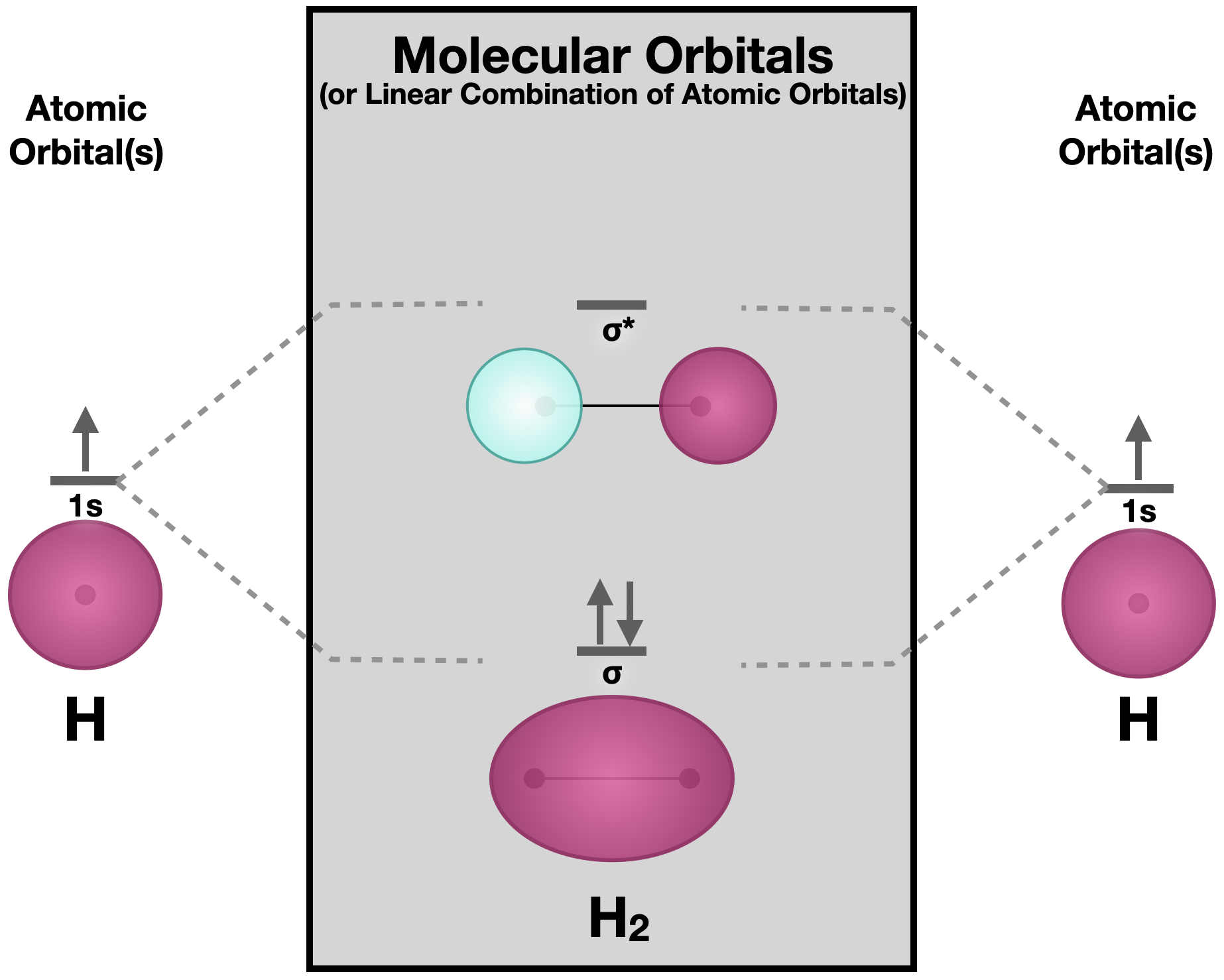    Молекулярна орбітальна діаграма дигідрогену. Дві атомні 1s орбіталі об'єднуються, щоб дати дві молекулярні орбіталі з сигма-симетрією. Орбіталь, що зв'язує сигму нижньої енергії, має обидва ядра, оточені електронною щільністю, тоді як орбітальна вища енергія має дві частки, які розділені вузлом.Теорія молекулярної орбіти

    Молекулярна орбітальна теорія (МО) - це складна модель зв'язку. Як правило, вважається більш потужним, ніж теорії Льюїса та Валентності Бонда для прогнозування молекулярних властивостей; однак ця сила приходить ціною складності. У своєму повному розвитку MO Theory вимагає складної математики, хоча ідеї, що стоять за нею, прості. Атомні орбіталі (AoS), які локалізуються на окремих атомах, об'єднуються, утворюючи молекулярні орбіталі (MoS), які розподіляються по молекулі. Найпростішим прикладом є молекула дигідрогену (H 2), в якій дві незалежні орбіталі водню 1s об'єднуються, утворюючи\(\sigma\) зв'язуючий МО і\(\sigma\) антизв'язуючий МО молекули дигідрогену (див. Рис.). MO також називаються лінійними комбінаціями атомних орбіталів (LCAO).