3.6: Метрика (частина 1)

Розглянемо координату x, визначену вздовж певної кривої, яка не обов'язково є геодезичною. Для конкретності уявіть, що ця крива існує у двох просторових вимірах, які ми можемо візуалізувати як поверхню сфери, вбудованої в евклідовий 3-простір. Ці конкретні особливості не є суворо необхідними, але вони рухають додому точку, яку ми не повинні очікувати, щоб ми могли визначити x, щоб він змінювався зі стійкою швидкістю з минулою відстанню; наприклад, ми знаємо, що неможливо буде визначити двовимірну декартову сітку на поверхні сфери. Таким чином, на малюнку галочки розташовані нерівномірно. Це абсолютно все гаразд, враховуючи координатну інваріантність загальної відносності. Оскільки інкрементні зміни в х рівні, я представив їх нижче кривої, як маленькі вектори однакової довжини. Вони є неправильною довжиною, щоб представляти відстані вздовж кривої, але ця неправильність є неминучим фактом життя в відносності.

Малюнок\(\PageIndex{1}\): Галочки на лінії визначають координату, виміряну вздовж лінії. Неможливо встановити таку систему координат глобально, щоб координата була рівномірною скрізь. Стрілки представляють зміни значення координати; так як зміни координати всі рівні, стрілки все однакової довжини.

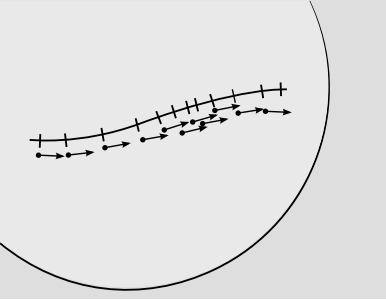
Тепер припустимо, ми хочемо інтегрувати довжину дуги сегмента цієї кривої. Маленькі вектори нескінченно малі. У інтегрованій довжині кожен маленький вектор повинен вносити певну суму, яка є скалярною. Цей скаляр - це не просто величина вектора\(ds \neq \sqrt{d \textbf{x} \cdot d \textbf{x}}\), так як вектори мають неправильну довжину. \(\PageIndex{1}\)Малюнок чітко нагадує геометричну картину векторів і подвійних векторів, розроблених раніше. Але чисто афінного поняття векторів та їх дуалів недостатньо для визначення довжини вектора загалом; достатньо лише визначити довжину відносно інших довжин уздовж тієї ж геодезичної. Коли вектори лежать уздовж різних геодезичних систем, нам потрібно вміти вказувати додатковий коефіцієнт перетворення, який дозволяє порівнювати один з іншим. Частина техніки, яка дозволяє нам це зробити, називається метрикою.

Фіксація метрики дозволяє нам визначити правильне масштабування галочок відносно стрілок у заданій точці, тобто в позначенні birdtracks це дає нам природний спосіб прийняття вектора переміщення, такого як →s, зі стрілкою, спрямованою на символ, і створення відповідного подвійного вектора s→, з стрілка виходить. Це трохи схоже на клонування людини, але робить клон протилежної статі. Підключення їх, як s → s, потім повідомляє нам квадратну величину вектора. Наприклад, якщо →dx є нескінченно малим тимчасовим зміщенням, то dx → dx - це квадратний часовий інтервал dx ², виміряний годинником, що рухається вздовж цього зміщення у просторі-часі. (Зауважте, що в позначенні dx ² зрозуміло, що dx є скаляром, тому що на відміну від →dx і dx→ він не має жодної стрілки, що входить або виходить з нього.) На малюнку\(\PageIndex{2}\) показана отримана картинка.

Малюнок\(\PageIndex{2}\): Вектори →dx і dx→ є подвійними один від одного.

У введеному раніше абстрактному позначенні індексу вектори →dx і dx→ записуються dx ^a і dx _a. Коли конкретна система координат була зафіксована, ми записуємо їх з конкретними, грецькими індексами,\(dx^\mu\) і\(dx_{\mu}\). У більш старих і концептуально несумісних позначеннях і термінології, обумовлених Сильвестром (1853), один відноситься\(dx_{\mu}\) як до контраваріантного вектора, і\(dx^\mu\) як коваріант. Заплутана термінологія узагальнена в Додатку C.

Припущення про те, що метрика існує, нетривіальне. Наприклад, у галілеївському просторовічасі немає метрики, оскільки в межі c → одиниці,\(\infty\) що використовуються для вимірювання часових та просторових переміщень, непорівнянні. Припускаючи, що існування метрики еквівалентно припущенню, що Всесвіт містить принаймні один фізично маніпульований годинник або лінійку, яку можна переміщати на великі відстані та прискорювати за бажанням. У далекому майбутньому великі і причинно ізольовані області космосу можуть містити тільки безмасові частинки, такі як фотони, які не можуть бути використані для побудови годинників (або, що еквівалентно, лінійки); фізика цих регіонів буде повністю описана без метрики. Якщо, з іншого боку, наш світ містить не просто нуль або один, а два або більше годин, то метрична гіпотеза вимагає, щоб ці годинники підтримували послідовну відносну швидкість при прискоренні вздовж тієї ж світової лінії. Ця послідовність - це те, що дозволяє нам думати про відносність як про теорію простору та часу, а не теорію годинників та лінійок. Існують і інші релятивістські теорії гравітації крім загальної теорії відносності, і деякі з них порушують цю гіпотезу.

Враховуючи dx ^\(\mu\), як ми знаходимо його подвійний dx _\(\mu\), і навпаки? В одному вимірі нам просто потрібно ввести дійсне число g як поправочний коефіцієнт. Якщо один з векторів коротший, ніж повинен бути в певній області, поправочний коефіцієнт служить для компенсації, роблячи його подвійним пропорційно довшим. Два можливих відображення (коваріантний до контраваріантного і контраваріантний до коваріантного) виконуються з факторами g та 1/g, а число g є метрикою, і воно кодує всю інформацію про відстані. Наприклад, якщо\(\phi\) представляє довготу, виміряну за полярним колом, то метрика є єдиним джерелом для бази, що зміщення d\(\phi\) відповідає 2540 км на радіан.

Тепер давайте узагальнимо більш ніж один вимір. Оскільки глобально декартові системи координат не можуть бути накладені на криволінійний простір, лінії постійних координат, як правило, не будуть ні рівномірно розташовані, ні перпендикулярні один одному. Якщо побудувати локальну множину базисних векторів, що лежать уздовж перетинів постійних координатних поверхонь, вони не утворюватимуть ортонормальну множину. Ми хотіли б мати вираз форми

\[ds^{2} = \sum dx^{\mu} dx_{\mu}\]

для квадратної довжини дуги, і за допомогою позначення підсумовування Ейнштейна це стає

\[ds^{2} = dx^{\mu} dx_{\mu}\]

Евклідова метрика

Для декартових\(\mu\) координат в евклідовій площині, де зазвичай не турбується про відмінність між коваріантними та контраваріантними векторами, цей вираз для\(ds^2\) є просто теоремою Піфагора, підсумована за двома значеннями двох координат:

\[ds^{2} = dx^{\mu} dx_{\mu} = dx^{2} + dy^{2}\]

Символи dx, ds ⁰, dx ⁰ та dx ₀ є синонімами, а також для dy, ds ¹, dx ¹ та dx ₁. (Оскільки позначення, такі як ds ¹, змушують читача відстежувати, які цифри були призначені яким літерам, краще використовувати позначення, такі як dy або ds ^y; останнє позначення в принципі можна сплутати з тим, в якому y була змінною, що приймає такі значення, як 0 або 1, але насправді ми розуміємо це з контексту, так само, як ми розуміємо, що d в не\(\frac{dy}{dx}\) мають на увазі деяку змінну d що означає число.)

У неевклідовому випадку теорема Піфагора помилкова;\(dx^\mu\) і вже не\(dx_\mu\) є синонімами, тому їх твір більше не є просто квадратом відстані. Щоб побачити це більш явно, давайте напишемо вираз так, щоб відбувалися тільки коваріантні величини. За локальною площинністю зв'язок між коваріантним і контраваріантним векторами є лінійним, і найбільш загальне співвідношення такого роду задається шляхом перетворення метрики симетричною матрицею\(g_{\mu \nu}\). Підставляючи\(dx_{\mu} = g_{\mu \nu} x^{\nu}\), ми маємо

\[ds^{2} = g_{\mu \nu} dx^{\mu} dx^{\nu}\]

де в даний час мається на увазі суми над μ і ν. Зверніть увагу, як передбачувані суми виникають лише тоді, коли повторюваний індекс виникає один раз у вигляді верхнього індексу та один раз як індекс; інші комбінації є неграматичними.

Вправа\(\PageIndex{1}\)

Самоперевірка: Чому має сенс вимагати, щоб метрика була симетричною?

Раніше ми стикалися з відмінністю між скалярами, векторами та подвійними векторами. Це конкретні приклади тензорів, які можуть бути виражені в позначенні birdtracks як об'єкти з m стрілками, що входять і n виходять, або. У позначеннях індексу ми маємо m надрядків і n індексів. Скаляр має m = n = 0. Подвійний вектор має (m, n) = (0, 1), вектор (1, 0) та метрику (0, 2). Число індексів ми називаємо рангом тензора. Тензори розглядаються більш детально, і визначені більш суворо, в главі 4. Для наших теперішніх цілей важливо зазначити, що саме тому, що ми пишемо символ з індексами або надіндексами, це не означає, що він заслуговує на те, щоб називатися тензором. Цей момент можна зрозуміти в більш елементарному контексті ньютонівських скалярів і векторів. Наприклад, ми можемо визначити евклідовий «вектор» u = (m, T, e), де m - маса Місяця, T - температура в Чикаго, а e - заряд електрона. Ця істота u не заслуговує на те, щоб називатися вектором, тому що вона не поводиться як вектор при обертанні. Загальна філософія полягає в тому, що тензор - це те, що має певні властивості при зміні координат. Наприклад, раніше ми вже бачили різну поведінку масштабування тензорів з рангами (1, 0), (0, 0) та (0, 1).

При обговоренні симетрії тензорів рангу-2 зручно вводити такі позначення:

\[T_{(ab)} = \frac{1}{2} (T_{ab} + T_{ba})\]

\[T_{[ab]} = \frac{1}{2} (T_{ab} - T_{ba})\]

Будь-який T _ab можна розділити на симетричні і антисиметричні частини. Це схоже на написання довільної функції як суми і непарної функції і парної функції. Метрика має лише симетричну частину: g _(ab) = g _ab, а g _[ab] = 0. Це позначення узагальнюється до рангів більше 2 пізніше.

Вправа\(\PageIndex{2}\)

Самоперевірка: Охарактеризуйте антисиметричний тензор 2 рангу у двох вимірах.

Приклад 7. Зміна масштабу

• Припустимо, ми почнемо з опису евклідової площини з певним набором декартових координат, але потім хочемо змінити на новий набір координат, які масштабуються порівняно з початковими. Як ефект від цього масштабування представлений в г?.
• Якщо ми змінимо наші одиниці виміру так\(x_{\mu} \rightarrow \alpha x^{\mu}\), щоб, при цьому вимагаючи, щоб ds ² вийшов однаковим, то нам потрібно\(g_{\mu \nu} \rightarrow \alpha^{−2} g_{\mu \nu}\).

Порівнюючи з розділом 2.1, ми виведемо загальне правило, що тензор рангу (m, n) перетворюється під масштабування шляхом підбору коефіцієнта\(\alpha^{m−n}\).

Все це поняття масштабування і одиниць в загальній теорії відносності виходить нетривіальним і цікавим. Докладніше про це можна дізнатися з розділу 5.11.

Приклад 8: полярні координати

Розглянемо полярні координати (r,\(\theta\)) в евклідовій площині. Криві постійної координати трапляються ортогональними скрізь, тому недіагональні елементи метрики g _r\(\theta\) і g _\(\theta\)r зникають. ^{Нескінченно малі зміни координат dr і d\(\theta\) відповідають нескінченно малим зміщенням dr і r d\(\theta\) в ортогональних напрямках, тому по теоремі Піфагора ds 2 = dr 2 + r\(\theta\) 2 d 2, і ми зчитуємо елементи метрики g} _рр = 1 і г _{\(\theta\)\(\theta\)}= р ².

Зверніть увагу, як у прикладі 8 ми почали з загальнодійсного відношення\(ds^{2} = g_{\mu \nu} dx^{\mu} dx^{\nu}\), але незабаром почали записувати факти, такі як g _{\(\theta\)\(\theta\)}= r ², які були дійсними лише в цій конкретній системі координат. Щоб зрозуміти, коли це відбувається, ми зберігаємо відмінність між абстрактними латинськими індексами та конкретними грецькими індексами, введеними раніше. Наприклад, ми можемо написати загальний вираз для квадратної довжини диференціальної дуги з латинськими індексами,

\[ds^{2} = g_{ij} dx^{i} dx^{j},\]

оскільки він тримається незалежно від системи координат, тоді як зникнення недіагональних елементів метрики в евклідових полярних координатах має бути записано як g _{\(\mu \nu\)}= 0 для\(\mu \neq \nu\), оскільки це взагалі буде помилковим, якщо ми використовували іншу систему координат для опису та ж евклідова площина.

Приклад 9: Косі декартові координати

Малюнок\(\PageIndex{3}\)

• Похилі декартові координати схожі на звичайні декартові координати в площині, але їх осі знаходяться під кутом одна\(\phi \neq \frac{\pi}{2}\) до одної. Знайдіть метрику в цих координатах. Простір глобально є евклідовим.
• Оскільки координати відрізняються від декартових координат тільки кутом між осями, а не в їх масштабах, зміщення dx ⁱ уздовж будь-якої осі, i = 1 або 2, має давати ds = dx, тому для діагональних елементів у нас g ₁₁ = g ₂₂ = 1. Метрика завжди симетрична, тому g ₁₂ = g ₂₁. Для фіксації цих позадіагональних елементів розглянемо зміщення на ds в напрямку, перпендикулярному осі 1. Це змінює координати на dx ¹ = − ds cot\(\phi\) і dx ² = ds cos\(\phi\). У нас тоді є

\[\begin{split} ds^{2} &= g_{ij} dx^{i} dx^{j} \\ &= ds^{2} (\cot^{2} \phi + csc^{2} \phi - 2g_{12} \cot \phi \csc \phi) \\ g_{12} &= \cos \phi \ldotp \end{split}\]

Приклад 10: площа

В одному вимірі g є єдиним числом, а довжини задаються ds =\(\sqrt{g}\) dx. Квадратний корінь також можна зрозуміти на прикладі 7, в якому ми побачили, що рівномірне масштабування x →\(\alpha\) x відображається в\(g_{\mu \nu} \rightarrow \alpha^{−2} g_{\mu \nu}\).

У двовимірних декартових координатах множення ширини і висоти прямокутника дає елемент площі\(dA = \sqrt{g_{11} g_{22}} dx^{1} dx^{2}\). Оскільки координати ортогональні, g - діагональ, а коефіцієнт\(\sqrt{g_{11} g_{22}}\) визначається як квадратний корінь його визначника, тому dA =\(\sqrt{|g|}\) dx ¹ dx ². Зверніть увагу, що шкали на двох осях не обов'язково однакові, g ₁₁ ≠ g ₂₂.

Той самий вираз для елемента області має місце, навіть якщо координати не ортогональні. У прикладі 9, наприклад, ми маємо\(\sqrt{|g|} = \sqrt{1 − \cos^{2} \phi} = \sin \phi\), який є правильним поправочним коефіцієнтом, що dx ¹ і dx ² утворюють паралелепіпед, а не прямокутник.

Приклад 11: площа сфери

Для координат\((\theta, \phi)\) на поверхні сфери радіуса r, ми маємо аргумент, подібний до того, що у прикладі 8\(g_{\theta \theta} = r^{2}, g_{\phi \phi} = r^{2} \sin^{2} \theta, g_{\theta \phi} = 0\). Площа сфери становить

\[\begin{split} A &= \int dA \\ &= \int \int \sqrt{|g|} d \theta d \phi \\ &= r^{2} \int \int \sin \theta d \theta d \phi \\ &= 4 \pi r^{2} \end{split}\]

Приклад 12: зворотна метрика

• ^{Віднесіть g in до г _ij.}
• Позначення призначене для лікування коваріантних і контраваріантних векторів повністю симетрично. Метрику з нижчими індексами g _ij можна інтерпретувати як трансформацію зміни базису з контраваріантної основи в коваріантну, а якщо симетрія позначення має бути збережена, g ^ij повинна бути відповідною оберненою матрицею, яка змінюється від коваріантної основи до контраваріантний. Метрика завжди повинна бути оборотною.

У одновимірному випадку метрика в будь-якій заданій точці була просто деяким числом g, і ми використовували множники g та 1/g для перетворення назад і вперед між коваріантними та контраваріантними векторами. Приклад 12 дає зрозуміти, як узагальнити це до більшої кількості вимірів:

\[\begin{split} x_{a} &= g_{ab} x^{b} \\ x^{a} &= g^{ab} x_{b} \end{split}\]

Це називається підвищенням і зниженням індексів. Немає необхідності запам'ятовувати позиції індексів у цих правилах; вони єдині можливі на основі граматичних правил, які полягають у тому, що підсумовування відбувається лише над парами верхнього та нижнього, а верхні та нижні індекси повинні збігатися з обох сторін знака рівності. Вся ця система, введена Ейнштейном, називається позначенням «індекс-гімнастика».

Приклад 13: Підвищення та зниження індексів на тензорі другого рангу

У фізиці ми зустрічаємо різні приклади матриць, такі як тензор моменту інерції з класичної механіки. Вони мають два індекси, а не лише один, як вектор. Знову ж таки, правила підвищення і зниження індексів випливають безпосередньо з граматики. Наприклад,

\[A^{a}_{b} = g^{ac} A_{cb}\]

і

\[A_{ab} = g_{ac} g_{bd} A^{cd} \ldotp\]

Приклад 14: Матриця, що працює на векторі

Вектори рядків і стовпців з лінійної алгебри є коваріантними та контраваріантними векторами в нашій сучасній термінології. (Угода полягає в тому, що коваріантні вектори - це вектори рядків та контраваріантні вектори стовпців, але я не вважаю, що це варто запам'ятовувати.) А як щодо матриць? Матриця, що діє на вектор стовпця, дає інший вектор стовпця, q = U p Переклавши це в індексну гімнастику позначення, ми маємо

\[q^{a} = U^{\ldots} \ldots p^{b},\]

де ми хочемо з'ясувати правильне розміщення індексів на U. граматично, єдино можливим розміщенням є

\[q^{a} = U^{a}_{b} p^{b} \ldotp\]

Це показує, що природним способом представлення лінійного оператора стовпчика-вектор-вектора-стовпця є тензор рангу 2 з одним верхнім індексом і одним нижнім індексом.

У позначеннях birdtracks тензор рангу-2 - це те, що має дві стрілки, з'єднані з ним. Нашим прикладом стає → q =→ U → p. Те, що результат є вектором верхнього індексу, показує той факт, що правий бік, взятий як ціле, має одну зовнішню стрілку, що входить в нього.

Різниця між векторами та їх дуалями може здатися неактуальною, якщо ми завжди можемо підвищувати та знижувати індекси за бажанням. Однак ми не завжди можемо це зробити, тому що в багатьох абсолютно звичайних ситуаціях немає метрики. Див. Приклад 6.

Музика Лоренца

У локально евклідовому просторі теорема Піфагора дозволяє висловити метрику в локальних декартових координатах в простій формі

\[g_\mu\mu = +1, g\mu\nu = 0\]

т. е.

\[g = diag(+1, +1, . . . , +1).\]

Це не є відповідним показником для локального простору Лоренца. Аксіоми евклідової геометрії Е3 (існування кіл) та Е4 (рівність прямих кутів) описують інваріантність теорії при обертаннях, і теорема Піфагора узгоджується з цим, оскільки вона дає однакову відповідь на довжину вектора, навіть якщо його компоненти перевиражені в новій основі, яка обертається щодо вихідного. Однак у лоренціанській геометрії ми дбаємо про інваріантність під імпульсами Лоренца, які не зберігають кількість\(t^2 + x^2\). Інваріантними є не кола в площині (t, x), а світлі конуси, і це описується наданням g _tt і g _xx протилежних знаків і рівних абсолютних знаків. Світлоподібний вектор (t, x), з t = x, отже, має величину рівно нуль

\[s^{2} = g_{tt} t^{2} + g_{xx} x^{2} = 0,\]

і це залишається вірним після імпульсу Лоренца (t, x) → (\(\gamma\)t,\(\gamma\) x). Це питання умовності, який елемент метрики зробити позитивним, а який - негативним. У цій книзі я використовую g _tt = +1 і g _xx = −1, так що g = diag (+1, −1). Це має ту перевагу, що будь-який відрізок лінії, що представляє часову світову лінію фізичного об'єкта, має позитивну величину в квадраті; прямий потік часу представлений як позитивне число, відповідно до філософії, що відносність - це в основному теорія того, як працюють причинно-наслідкові зв'язки. З цією конвенцією про знак, космічні вектори мають позитивні квадратні величини, схожі на час - негативні. Цією ж конвенцією дотримується, наприклад, Пенроуз. Протилежна версія, з g = diag (−1, +1) використовується такими авторами, як Вальд і Міснер, Торн і Вілер.

Наш Всесвіт не має лише одного просторового виміру, він має три, тому повна метрика в кадрі Лоренца задається

\[g = diag(+1, −1, −1, −1).\]

Приклад 15: Змішана коваріативно-контраваріантна форма метрики

У прикладі 13 ми бачили, як підвищувати і знижувати індекси на тензорі другого рангу, а приклад 14 показав, що іноді природно розглядати форму, в якій піднімається один індекс, а один знижений. Метрика сама по собі є тензором другого рангу, тому давайте подивимося, що відбувається, коли ми обчислюємо змішану форму g ^a _b з нижнього індексу форми. Загалом, у нас

\[A^{a}_{b} = g^{ac} A_{cb},\]

і підставляючи g на A дає

\[g_{b}^{a} = g^{ac} g_{cb} \ldotp\]

Але ми вже знаємо, що г^... це просто обернена матриця г_... (приклад 12), що означає, що g ^a _b - це просто матриця ідентичності. Тобто, тоді як така величина, як g _ab або g ^ab, несе всю інформацію про нашу систему вимірювання в заданій точці, g ^a _b не несе ніякої інформації взагалі. Там, де g _ab ^{або g ab} можуть мати як позитивні, так і негативні елементи, елементи, які мають одиниці, і поза діагоналлю елементи, g ^a _b є лише загальним символом, що несе ніякої інформації, крім розмірності простору.

Метричний тензор настільки часто використовується, що він просто залишається поза діаграмами пташиних доріжок. Послідовність зберігається, оскільки g ^a _b є матрицею ідентичності, тому → g → збігається з →.