3.3: Аффінні поняття та паралельний транспорт

Last updated
Save as PDF

Page ID: 77503

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Аффінний параметр у вигнутому просторовому часі: грубий ескіз

Ми хочемо мати можливість вимірювати речі у вигнутому просторучасі. Виявляються дві взаємодоповнюючі системи вимірювання, які ми можемо застосувати: афінна міра та метрична міра. Аффінна міра в плоскій геометрії була введена в Розділі 2.1. Дивно, але, виявляється, досить легко узагальнити це до криволінійного випадку. Наша побудова афінного параметра з риштуванням паралелограм залежала від існування і унікальності паралелей, виражених аксіомою А1, тому ми могли б уявити, що немає сенсу намагатися узагальнювати конструкцію до криволінійного просторучасу. Але принцип еквівалентності говорить нам, що просторовийчас локально афінний до деякого наближення. Конкретно, годинник часу є одним із прикладів афінного параметра, і кривизна простору-часу явно не може перешкодити нам побудувати годинник і випустити його на траєкторію вільного падіння.

У загальному плані ми можемо використовувати той факт, що кожен сегмент геодезичної ділянки геометрично схожий на будь-який інший сегмент. Наприклад, розглянемо дугу земного екватора, що охоплює один градус довготи. Ця дуга може бути ковзана вздовж екватора до іншого місця, а потім розширена, щоб покрити 3 градуси довготи. Дві дуги схожі.

Приклад 2: Геодезичні особливості

Наступні три неприклади показують, що це особлива властивість геодезичних робіт.

Властивістю не користується негеодезична крива. Відрізок п'ятикутника, який охоплює одну з вершин, не схожий на якийсь інший відрізок, який є прямим.

Іншим неприкладом, що включає негеодезичні, є крива, яку ми отримуємо в 1+1-мірному просторовічасі, з'єднавши разом позитивну вісь x та позитивну вісь t. Ми ніколи не можемо взяти однорічний відрізок осі t і через будь-яку комбінацію прискорень і обертань змусити його збігатися з однорічним шматочком осі x. Оригінальний сегмент - це timelike, і будь-який імпульс або обертання збереже свій часовий характер.

Крім того, загалом неправда, коли існує кривизна, ми можемо взяти будь-яку геометричну фігуру, транспортувати її куди завгодно, а також масштабувати її, як нам подобається. Наприклад, евклідова геометрія є хорошим наближенням на невеликих ділянках сферичної поверхні Землі, тому дорожню карту можна скласти у формі прямокутника з чотирма прямокутними кутами. Однак масштабувати такий прямокутник неможливо; щоб відобразити значну частину світу, ми повинні ввести спотворення типу, що використовується в картографічних проекціях.

Оскільки геодезичні мають цю особливу властивість, ми можемо пересунути будь-яку ділянку геодезичної в будь-яке інше місце геодезичної та використовувати її як стандартну міру. Це дає нам повну систему вимірювань уздовж цієї геодезичної, і вона працює незалежно від того, чи є геодезична є часовою, світлоподібною чи космічною. Але як і в плоскій геометрії, афінне вимірювання не дозволяє порівнювати довжини по одній геодезичній довжині з довжинами по іншій.

Афінний параметр більш детально

Коли ми спочатку визначили афінну міру в розділі 2.1, для плоского простору ми зробили це через явну конструкцію риштування. Важливим прикладом диференціальної, тобто локальної, природи нашої геометрії є узагальнення конструкції риштування від до контексту ширшого, ніж аффінна геометрія.

Для узагальнення рецепта побудови (рис. 3.2.1) першою перешкодою є неоднозначність інструкції побудови паралелограма\((0,1,q_0,q_1)\), яка вимагає провести 1q ₁ паралельно 0q ₀. Припустимо, ми тлумачимо це як інструкцію зробити два сегменти спочатку паралельними, тобто паралельними, коли вони відходять від лінії 0 та 1. До того моменту, коли вони досягають q ₀ і q ₁, вони можуть бути сходяться або розходяться.

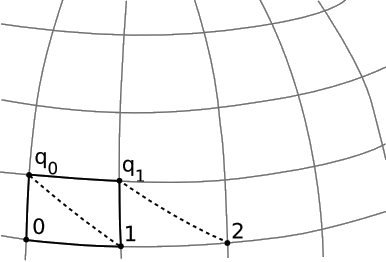
3.2.1.png — Малюнок\(\PageIndex{1}\) - Побудова афінного параметра в криволінійному просторовічасу.

Оскільки паралелізм тут лише приблизний, у побудові афінного параметра буде певна похибка. Одним із способів виявлення такої помилки є те, що решітки, побудовані з різними початковими відстанями, будуть виходити з кроку одна з одною. Наприклад, ми можемо визначити,\(\frac{1}{2}\) як і раніше, вимагаючи, щоб решітка, побудована з початковим відрізком 0,\(\frac{1}{2}\) вирівнювалася з вихідною решіткою на 1. Однак ми виявимо, що вони не зовсім шикуються в інших точках, таких як 2. Давайте використаємо цю невідповідність\(\epsilon\) = 2 − 2' як числову міру похибки. Це буде залежати як\(\delta_{1}\) від відстані 01, так і від\(\delta_{2}\), відстані між 0 і q ₀. Оскільки\(\epsilon\) зникає для або\(\delta_{1}\) = 0 або\(\delta_{2}\) = 0, а оскільки принцип еквівалентності гарантує плавну поведінку на малих масштабах, провідний термін у похибці в цілому буде пропорційним добутку\(\delta_{1} \delta_{2}\). Мовою нескінченності ми можемо замінити\(\delta_{1}\) і\(\delta_{2}\) з нескінченно короткими відстанями, які для простоти ми вважаємо рівними, і які ми називаємо d\(\lambda\). Тоді\(\lambda\) афінний параметр визначається як\(\lambda = \int d \lambda\), де похибка порядку d\(\lambda^{2}\), як зазвичай, інтерпретується як незначна невідповідність інтеграла та його наближення як сума Рімана.

Паралельний транспорт

Якщо ви були насторожені, ви, можливо, зрозуміли, що я обдурив вас у вирішальний момент цієї конструкції. Ми повинні були зробити 1q ₁ і 0q ₀ «спочатку паралельно», як вони залишили 01. Як нам взагалі визначити цю ідею «спочатку паралельно?» Ми могли б спробувати зробити це, зробивши кути q ₀ 01 і q ₁ 12 рівними, але це не зовсім працює, тому що він не вказує, чи кут ліворуч чи праворуч на двовимірній площині сторінки. У трьох і більше вимірах питання стає ще більш серйозним. Будівельні робітники, які будують решітку, повинні тримати все це в одній площині, але як вони це роблять у вигнутому простору-часі?

Відповідь математика полягає в тому, що наша геометрія не має деякої додаткової структури, яка називається зв'язком, що є правилом, яке визначає, як одна локально плоска околиця повинна бути об'єднана безперешкодно до іншого локально плоского сусідства поблизу. Якщо ви коли-небудь купували дві карти і намагалися склеїти їх разом, щоб зробити велику карту, ви сформували з'єднання. Якщо карти були в досить великому масштабі, ви також напевно помітили, що це неможливо зробити ідеально, через кривизну землі.

Фізично ідея полягає в тому, що в умовах плоского просторучасу можна побудувати інерційні системи наведення, як ті, що обговорювалися раніше. Оскільки вони можливі в рівному просторовому часі, вони також можливі в місцевих рівнинних районах простору-часу, а потім їх можна переносити з одного району в інший. У трьох вимірах простору вектор кутового імпульсу гіроскопа зберігає свій напрямок, і ми можемо зорієнтувати інші вектори, такі як 1q ₁, відносно нього. Припустимо для конкретності, що побудова афінного параметра вище ведеться в трьох вимірах простору. Розміщуємо гіроскоп на 0, орієнтуємо його вісь вздовж 0q ₀, просуваємо його уздовж лінії до 1, а потім будуємо 1q ₁ вздовж цієї осі.

У розмірах 3+1 гіроскоп виконує лише частину роботи. Тепер нам належить зберегти напрямок чотиривимірного вектора. Чотири вектори не будуть детально розглядатися до розділу 4.2, але подібні пристрої можна використовувати для підтримки їх орієнтації в просторі-часі. Ці фізичні пристрої є способами визначення математичного поняття, відомого як паралельний транспорт, що дозволяє нам приймати вектор з однієї точки в іншу в просторі. Загалом, вказівка поняття паралельного транспорту еквівалентно вказівці з'єднання.

Паралельний транспорт залежить від шляху, як показано на малюнку 3.2.2.

3.2.2.png — Малюнок\(\PageIndex{2}\) - Паралельний транспорт залежить від шляху. На поверхні цієї сфери паралельно транспортує вектор по АВС дає іншу відповідь, ніж транспортування його по змінному струму.

Аффінні параметри, визначені тільки уздовж геодезичних

У контексті плоского просторучасу афінний параметр визначався лише вздовж ліній, а не довільних кривих, і не міг бути зіставлений між лініями, що йдуть в різні боки. У криволінійному просторучасі присутній таке ж обмеження, але з «уздовж ліній» замінені на «уздовж геодезики». На малюнку 3.2.3 показано, що піде не так, якщо ми спробуємо застосувати будівництво до світової лінії, яка не є геодезичною. Одне визначення геодезичного полягає в тому, що це курс, який ми в кінцевому підсумку будемо слідувати, якщо ми орієнтуємося, зберігаючи фіксований підшипник щодо інерційного пристрою наведення, такого як гіроскоп; тобто дотична до геодезичного, коли паралельно транспортується далі уздовж геодезичного, все ще дотична. Негеодезична крива не має цієї властивості, і вплив на побудову афінного параметра полягає в тому, що сегменти nq _n дрейфують все більше і більше поза вирівнюванням з кривою.

3.2.3.png — Малюнок 3.2.2. Паралельний транспорт не зберігає кут векторів відносно кривої, як це було б у геодезичному. Помилки в будівництві вибухають таким чином, що б не сталося, якби крива була геодезичною. Четверта пунктирна паралель дико злітає навколо задньої частини сфери, обертаючись навколо і зустрічаючи криву в точці, 4, тобто по суті випадково.