Skip to main content
LibreTexts - Ukrayinska

19.5: Рух на циклоїді, розвороти вгору

  1. Last updated
  2. Save as PDF
  • Page ID
    76387

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Ми уявімо або частинку, що ковзає всередину гладкої циклоїдної чаші, або кульку, що ковзає вниз гладкою циклоїдною дротом, рис. XIX.6.

    альт

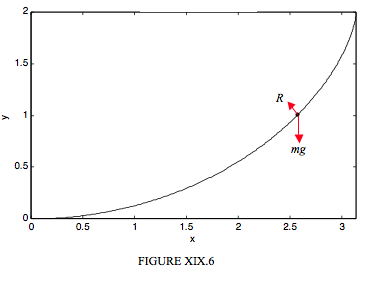
    Ми працюватимемо у власних координатах, щоб отримати тангенціальні та нормальні рівняння руху. Ці рівняння, відповідно:

    \[ \ddot{s} = -g \sin \psi \label{19.5.1}\tag{19.5.1} \]

    і

    \[ \dfrac{mv^2}{ \rho} = R - mg \cos \psi. \label{19.5.2}\tag{19.5.2} \]

    Тут R - нормальна (і єдина) реакція чаші або дроту на частинку і\( \rho \) є радіусом кривизни. Радіус кривизни дорівнює\(ds/d \psi \), який, з Рівняння 19.3.1, (або Рівняння 19.4.3 і 19.4.5) дорівнює

    \[ \rho = 4 a \cos \psi \label{19.5.3}\tag{19.5.3} \]

    З Рівняння 19.3.1 і\(\ref{19.5.1}\) ми бачимо, що тангенціальне рівняння руху можна записати без наближення:

    \[\ddot{s} = -\dfrac{g}{4a}s. \label{19.5.4}\tag{19.5.4} \]

    Це простий гармонійний рух періоду\( 4 \pi \sqrt{a/g} \), незалежний від амплітуди руху. У цьому полягає ізохронна властивість циклоїда. Так само, якщо частка звільниться від спокою, вона досягне дна циклоїди за час\( \pi \sqrt{a/g} \) незалежно від вихідного положення.

    Давайте подивимося, чи зможемо ми знайти значення R, де генерує кут\( \psi \). Припустимо, що частка звільняється від спокою на висоті\(y_0\) над\(x\) віссю -( кут генерації =\( \psi_0\)); яка її швидкість,\(v\) коли вона досягла висоти\(y\) (генеруючого кута\( \psi \))? Зрозуміло, що це дає

    \[ \dfrac{1}{2} mv^2 = mg(y_0 - y), \label{19.5.5}\tag{19.5.5} \]

    і, слідуючи рівнянню 19.3.2, і нагадуючи\( \theta = \psi \), що, це

    \[ v^2 = 2ga(cos2 \psi - cos2 \psi_0 ). \label{19.5.6}\tag{19.5.6} \]

    Підставивши це і Рівняння\( \ref{19.5.3} \) в рівняння\( \ref{19.5.2}\), ми знаходимо для R:

    \[ R = \frac{mg}{2 \cos \psi }(1+ 2 \cos 2 \psi - \cos 2 \psi_0) \label{19.5.7}\tag{19.5.7} \]