11.1: Параметричні рівняння
- Page ID
- 61752
- Побудуйте криву, описану параметричними рівняннями.
- Перетворіть параметричні рівняння кривої в форму\(y=f(x)\).
- Розпізнайте параметричні рівняння основних кривих, таких як лінія і коло.
- Розпізнайте параметричні рівняння циклоїди.
У цьому розділі ми розглянемо параметричні рівняння та їх графіки. У двовимірній системі координат параметричні рівняння корисні для опису кривих, які не обов'язково є функціями. Параметр є незалежною змінною, яка\(x\) і\(y\) залежить від, і в міру збільшення параметра значення\(x\) і\(y\) трасування шляху вздовж плоської кривої. Наприклад, якщо параметр є\(t\) (загальний вибір), то\(t\) може представляти час. Потім\(x\) і\(y\) визначаються як функції часу, і\((x(t),y(t))\) можуть описати положення в площині даного об'єкта, коли він рухається по криволінійному шляху.
Параметричні рівняння та їх графіки
Розглянемо орбіту Землі навколо Сонця. Наш рік триває приблизно 365,25 днів, але для цього обговорення ми будемо використовувати 365 днів. 1 січня кожного року фізичне розташування Землі по відношенню до Сонця майже однакове, за винятком високосних років, коли в календар вбудовується відставання, введене додатковим\(\frac{1}{4}\) днем орбітального часу. Ми називаємо 1 січня «днем 1» року. Тоді, наприклад, 31 день - 31 січня, день 59 - 28 лютого і так далі.
Число доби в році можна вважати змінною, яка визначає положення Землі на її орбіті. Коли Земля обертається навколо Сонця, її фізичне розташування змінюється відносно Сонця. Після одного цілого року ми повернулися туди, де починали, і починається новий рік. За законами Кеплера планетарного руху форма орбіти еліптична, при цьому Сонце знаходиться в одному фокусі еліпса. Вивчаємо цю ідею більш детально в конічних перерізах.
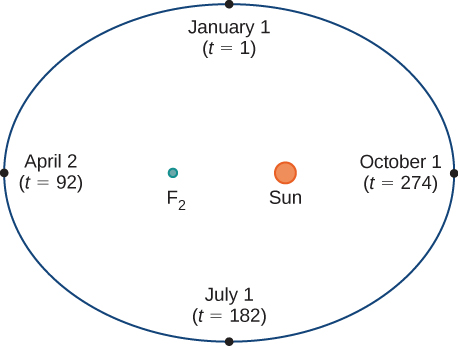
Малюнок\( \PageIndex{1}\) зображує орбіту Землі навколо Сонця протягом одного року. \(F_2\)Позначена точка є одним з вогнищ еліпса; інший фокус займає Сонце. Якщо ми накладемо координатні осі над цим графіком, то ми можемо призначити впорядковані пари кожній точці еліпса (рис.\( \PageIndex{2}\)). Тоді кожне\(x\) значення на графіку є значенням позиції як функції часу, і кожне\(y\) значення також є значенням позиції як функції часу. Тому кожній точці на графіку відповідає значення положення Землі як функція часу.
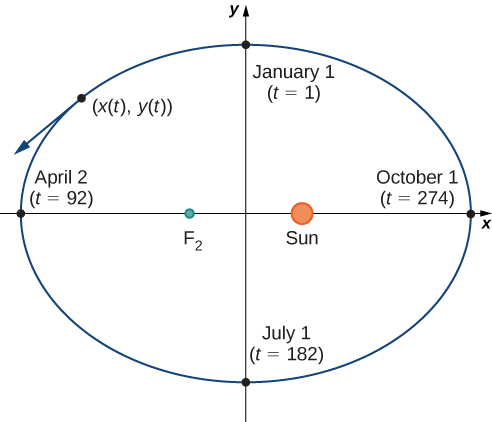
Ми можемо визначити функції для\(x(t)\) і\(y(t)\), тим самим параметризуючи орбіту Землі навколо Сонця. Змінна\(t\) називається незалежним параметром і в цьому контексті представляє час щодо початку кожного року.
Криву в\((x,y)\) площині можна представити параметрично. Рівняння, які використовуються для визначення кривої, називаються параметричними рівняннями.
Якщо\(x\) і\(y\) є неперервними функціями\(t\) на інтервалі\(I\), то рівняння
\[x=x(t) \nonumber \]
і
\[y=y(t) \nonumber \]
називаються параметричними рівняннями і\(t\) називаються параметром. Множина точок,\((x,y)\) отриманих як\(t\) змінюється за інтервалом\(I\), називається графіком параметричних рівнянь. Графік параметричних рівнянь називається параметричної кривою або плоской кривою, і позначається знаком\(C\).
Зверніть увагу в цьому визначенні, що\(x\) і\(y\) використовуються двома способами. Перший - як функції незалежної змінної\(t\). Як\(t\) змінюється протягом інтервалу\(I\), функції\(x(t)\) і\(y(t)\) генерують набір впорядкованих пар\((x,y)\). Ця множина впорядкованих пар генерує графік параметричних рівнянь. У цьому другому використанні, щоб позначити впорядковані пари,\(x\) і\(y\) є змінними. Важливо відрізняти змінні\(x\) і\(y\) від функцій\(x(t)\) і\(y(t)\).
Намалюйте криві, описані наступними параметричними рівняннями:
- \(x(t)=t−1, \quad y(t)=2t+4,\quad \text{for }−3≤t≤2\)
- \(x(t)=t^2−3, \quad y(t)=2t+1,\quad \text{for }−2≤t≤3\)
- \(x(t)=4 \cos t, \quad y(t)=4 \sin t,\quad \text{for }0≤t≤2π\)
Рішення
а Щоб створити графік цієї кривої, спочатку створіть таблицю значень. Оскільки незалежна змінна в обох\(x(t)\) і\(y(t)\) є\(t\), нехай\(t\) з'являться в першому стовпці. Потім\(x(t)\) і\(y(t)\) з'явиться у другому і третьому стовпцях таблиці.
| \(t\) | \(x(t)\) | \(y(t)\) |
|---|---|---|
| \ (t\)» style="вертикальне вирівнювання: середина; ">−3 | \ (x (t)\)» style="вертикальне вирівнювання: середина; ">−4 | \ (y (t)\)» style="вертикальне вирівнювання: середина; ">−2 |
| \ (t\)» style="вертикальне вирівнювання: середина; ">−2 | \ (x (t)\)» style="вертикальне вирівнювання: середина; ">−3 | \ (y (t)\)» style="вертикальне вирівнювання: середина; "> 0 |
| \ (t\)» style="вертикальне вирівнювання: середина; ">−1 | \ (x (t)\)» style="вертикальне вирівнювання: середина; ">−2 | \ (y (t)\)» style="вертикальне вирівнювання: середина; "> 2 |
| \ (t\)» style="вертикальне вирівнювання: середина; "> 0 | \ (x (t)\)» style="вертикальне вирівнювання: середина; ">−1 | \ (y (t)\)» style="вертикальне вирівнювання: середина; "> 4 |
| \ (t\)» style="вертикальне вирівнювання: середина; "> 1 | \ (x (t)\)» style="вертикальне вирівнювання: середина; "> 0 | \ (y (t)\)» style="вертикальне вирівнювання: середина; "> 6 |
| \ (t\)» style="вертикальне вирівнювання: середина; "> 2 | \ (x (t)\)» style="вертикальне вирівнювання: середина; "> 1 | \ (y (t)\)» style="вертикальне вирівнювання: середина; "> 8 |
Другий і третій стовпці цієї таблиці надають набір точок для побудови графіка. Графік цих точок відображається на рис\( \PageIndex{3}\). Стрілки на графіку вказують на орієнтацію графіка, тобто напрямок руху точки на графіку, коли t змінюється від −3 до 2.
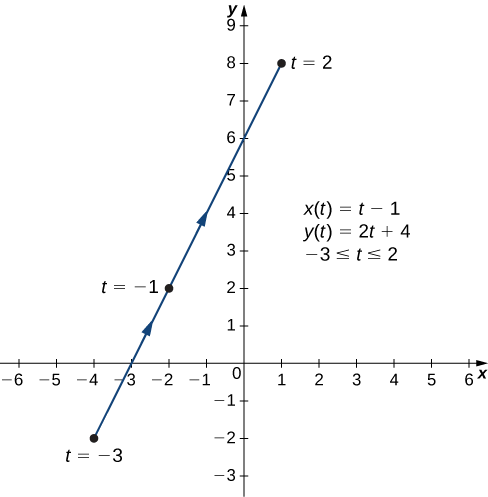
б Щоб створити графік цієї кривої, знову налаштуйте таблицю значень.
| \(t\) | \(x(t)\) | \(y(t)\) |
|---|---|---|
| \ (t\)» style="вертикальне вирівнювання: середина; ">−2 | \ (x (t)\)» style="вертикальне вирівнювання: середина; "> 1 | \ (y (t)\)» style="вертикальне вирівнювання: середина; ">−3 |
| \ (t\)» style="вертикальне вирівнювання: середина; ">−1 | \ (x (t)\)» style="вертикальне вирівнювання: середина; ">−2 | \ (y (t)\)» style="вертикальне вирівнювання: середина; ">−1 |
| \ (t\)» style="вертикальне вирівнювання: середина; "> 0 | \ (x (t)\)» style="вертикальне вирівнювання: середина; ">−3 | \ (y (t)\)» style="вертикальне вирівнювання: середина; "> 1 |
| \ (t\)» style="вертикальне вирівнювання: середина; "> 1 | \ (x (t)\)» style="вертикальне вирівнювання: середина; ">−2 | \ (y (t)\)» style="вертикальне вирівнювання: середина; "> 3 |
| \ (t\)» style="вертикальне вирівнювання: середина; "> 2 | \ (x (t)\)» style="вертикальне вирівнювання: середина; "> 1 | \ (y (t)\)» style="вертикальне вирівнювання: середина; "> 5 |
| \ (t\)» style="вертикальне вирівнювання: середина; "> 3 | \ (x (t)\)» style="вертикальне вирівнювання: середина; "> 6 | \ (y (t)\)» style="вертикальне вирівнювання: середина; "> 7 |
Другий і третій стовпці в цій таблиці дають набір точок, що підлягають нанесенню (рис.\( \PageIndex{4}\)). Перша точка на графіку (відповідна\(t=−2\)) має координати\((1,−3)\), а остання точка (відповідна\(t=3\)) має координати\((6,7)\). У\(t\) міру просування від\(−2\) до\(3\) точка на кривій рухається вздовж параболи. Напрямок, в якому рухається точка, знову називається орієнтацією і вказується на графіку.
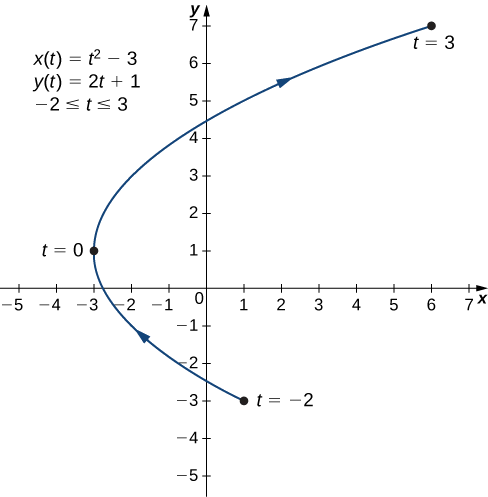
c У цьому випадку використовуйте кратні\(π/6\) for\(t\) і створіть іншу таблицю значень:
| \(t\) | \(x(t)\) | \(y(t)\) | \(t\) | \(x(t)\) | \(y(t)\) |
|---|---|---|---|---|---|
| \ (t\)» style="вертикальне вирівнювання: середина; "> 0 | \ (x (t)\)» style="вертикальне вирівнювання: середина; "> 4 | \ (y (t)\)» style="вертикальне вирівнювання: середина; "> 0 | \ (t\)» style="вертикальне вирівнювання: середина; ">\(\frac{7π}{6}\) | \ (x (t)\)» style="вертикальне вирівнювання: середина; ">\(-2\sqrt{3}≈−3.5\) | \ (y (t)\)» style="вертикальне вирівнювання: середина; ">-2 |
| \ (t\)» style="вертикальне вирівнювання: середина; ">\(\frac{π}{6}\) | \ (x (t)\)» style="вертикальне вирівнювання: середина; ">\(2\sqrt{3}≈3.5\) | \ (y (t)\)» style="вертикальне вирівнювання: середина; "> 2 | \ (t\)» style="вертикальне вирівнювання: середина; ">\(\frac{4π}{3}\) | \ (x (t)\)» style="вертикальне вирівнювання: середина; ">−2 | \ (y (t)\)» style="вертикальне вирівнювання: середина; ">\(−2\sqrt{3}≈−3.5\) |
| \ (t\)» style="вертикальне вирівнювання: середина; ">\(\frac{π}{3}\) | \ (x (t)\)» style="вертикальне вирівнювання: середина; "> 2 | \ (y (t)\)» style="вертикальне вирівнювання: середина; ">\(2\sqrt{3}≈3.5\) | \ (t\)» style="вертикальне вирівнювання: середина; ">\(\frac{3π}{2}\) | \ (x (t)\)» style="вертикальне вирівнювання: середина; "> 0 | \ (y (t)\)» style="вертикальне вирівнювання: середина; ">−4 |
| \ (t\)» style="вертикальне вирівнювання: середина; ">\(\frac{π}{2}\) | \ (x (t)\)» style="вертикальне вирівнювання: середина; "> 0 | \ (y (t)\)» style="вертикальне вирівнювання: середина; "> 4 | \ (t\)» style="вертикальне вирівнювання: середина; ">\(\frac{5π}{3}\) | \ (x (t)\)» style="вертикальне вирівнювання: середина; "> 2 | \ (y (t)\)» style="вертикальне вирівнювання: середина; ">\(−2\sqrt{3}≈−3.5\) |
| \ (t\)» style="вертикальне вирівнювання: середина; ">\(\frac{2π}{3}\) | \ (x (t)\)» style="вертикальне вирівнювання: середина; ">−2 | \ (y (t)\)» style="вертикальне вирівнювання: середина; ">\(2\sqrt{3}≈3.5\) | \ (t\)» style="вертикальне вирівнювання: середина; ">\(\frac{11π}{6}\) | \ (x (t)\)» style="вертикальне вирівнювання: середина; ">\(2\sqrt{3}≈3.5\) | \ (y (t)\)» style="вертикальне вирівнювання: середина; ">-2 |
| \ (t\)» style="вертикальне вирівнювання: середина; ">\(\frac{5π}{6}\) | \ (x (t)\)» style="вертикальне вирівнювання: середина; ">\(−2\sqrt{3}≈−3.5\) | \ (y (t)\)» style="вертикальне вирівнювання: середина; "> 2 | \ (t\)» style="вертикальне вирівнювання: середина; ">\(2π\) | \ (x (t)\)» style="вертикальне вирівнювання: середина; "> 4 | \ (y (t)\)» style="вертикальне вирівнювання: середина; "> 0 |
| \ (t\)» style="вертикальне вирівнювання: середина; ">\(π\) | \ (x (t)\)» style="вертикальне вирівнювання: середина; ">−4 | \ (y (t)\)» style="вертикальне вирівнювання: середина; "> 0 | \ (t\)» style="вертикальне вирівнювання: середина; "> | \ (x (t)\)» style="вертикальне вирівнювання: середина; "> | \ (y (t)\)» style="вертикальне вирівнювання: середина; "> |
Графік цієї плоської кривої відображається на наступному графіку.
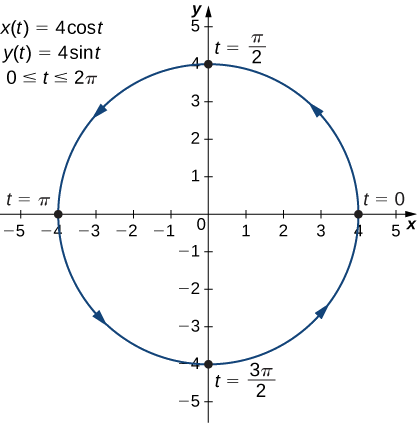
Це графік кола з радіусом,\(4\) центрованим у початковій точці, з орієнтацією проти годинникової стрілки. Початкова і кінцева точки кривої мають координати\((4,0)\).
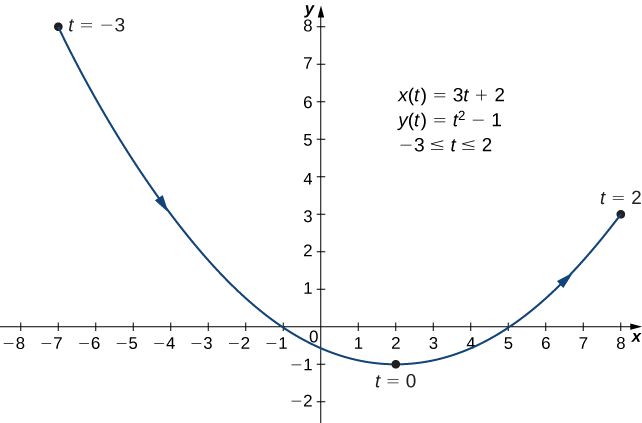
Намалюйте криву, описану параметричними рівняннями
\[ x(t)=3t+2,\quad y(t)=t^2−1,\quad \text{for }−3≤t≤2. \nonumber \]
- Підказка
-
Складіть таблицю значень для\(x(t)\) і\(y(t)\) використання\(t\) значень від\(−3\) до\(2\).
- Відповідь
-
Усунення параметра
Щоб краще зрозуміти графік кривої, представленої параметрично, корисно переписати два рівняння як єдине рівняння, що стосується змінних\(x\) і\(y\). Тоді ми можемо застосувати будь-які попередні знання рівнянь кривих в площині для ідентифікації кривої. Наприклад, рівняння, що описують плоску криву в\(\PageIndex{1b}\) прикладі, є
\[\begin{align} x(t) &=t^2−3 \label{x1} \\[4pt] y(t) &=2t+1 \label{y1} \end{align} \]
над регіоном\(-2 \le t \le 3.\)
Розв'язування рівняння\ ref {y1} для\(t\) дає
\[t=\dfrac{y−1}{2}. \nonumber \]
Це можна замінити на рівняння\ ref {x1}:
\[\begin{align} x &=\left(\dfrac{y−1}{2}\right)^2−3 \\[4pt] &=\dfrac{y^2−2y+1}{4}−3 \\[4pt] &=\dfrac{y^2−2y−11}{4}. \label{y2}\end{align} \]
Рівняння\ ref {y2} описує\(x\) як функцію\(y\). Ці кроки наводять приклад усунення параметра. Графік цієї функції - парабола, що відкривається вправо (рис.\(\PageIndex{4}\)). Нагадаємо, що плоска крива почалася\((1,−3)\) і закінчилася в\((6,7)\). Ці закінчення були обумовлені обмеженням по параметру\(t\).
Виключіть параметр для кожної з плоских кривих, описаних наступними параметричними рівняннями, і опишіть отриманий графік.
- \(x(t)=\sqrt{2t+4}, \quad y(t)=2t+1,\quad \text{for }−2≤t≤6\)
- \(x(t)=4\cos t, \quad y(t)=3\sin t,\quad \text{for }0≤t≤2π\)
Рішення
а Щоб усунути параметр, ми можемо вирішити будь-яке з рівнянь для\(t\). Наприклад, рішення першого рівняння для\(t\) дає
\[\begin{align*} x &=\sqrt{2t+4} \\[4pt] x^2 &=2t+4 \\[4pt] x^2−4 &=2t \\[4pt] t &=\dfrac{x^2−4}{2}. \end{align*}\]
Зверніть увагу, що коли ми квадратуємо обидві сторони, важливо це дотримуватися\(x≥0\). Заміна\(t=\dfrac{x^2−4}{2}\) на\(y(t)\) врожайність
\[ y(t)=2t+1 \nonumber \]
\[ y=2\left(\dfrac{x^2−4}{2}\right)+1 \nonumber \]
\[ y=x^2−4+1 \nonumber \]
\[ y=x^2−3. \nonumber \]
Це рівняння параболи, що відкривається вгору. Однак існує обмеження домену через обмеження на параметр\(t\). Коли\(t=−2\)\(x=\sqrt{2(−2)+4}=0\), і коли\(t=6\),\(x=\sqrt{2(6)+4}=4\). Далі йде графік цієї плоської кривої.
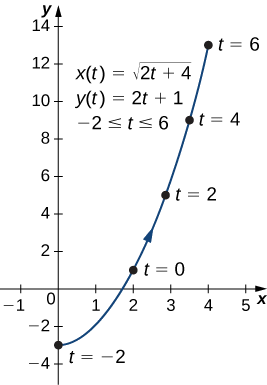
б. іноді необхідно проявити трохи творчий підхід до усунення параметра. Параметричні рівняння для цього прикладу
\[ x(t)=4 \cos t\nonumber \]
і
\[ y(t)=3 \sin t\nonumber \]
Вирішення будь-якого рівняння для\(t\) безпосередньо не доцільно, оскільки синус і косинус не є функціями один до одного. Однак ділення першого рівняння на,\(4\) а друге рівняння на\(3\) (і придушення\(t\)) дає нам
\[ \cos t=\dfrac{x}{4}\nonumber \]
і
\[ \sin t=\dfrac{y}{3}.\nonumber \]
Тепер використовуйте піфагорійську ідентичність\(\cos^2t+\sin^2t=1\) і замініть вирази для\(\sin t\) і\(\cos t\) з еквівалентними виразами з точки зору\(x\) і\(y\). Це дає
\[ \left(\dfrac{x}{4}\right)^2+\left(\dfrac{y}{3}\right)^2=1 \nonumber \]
\[ \dfrac{x^2}{16}+\dfrac{y^2}{9}=1. \nonumber \]
Це рівняння горизонтального еліпса, зосередженого на початку, з напіввеликою віссю\(4\) та напівмалою віссю,\(3\) як показано на наступному графіку.
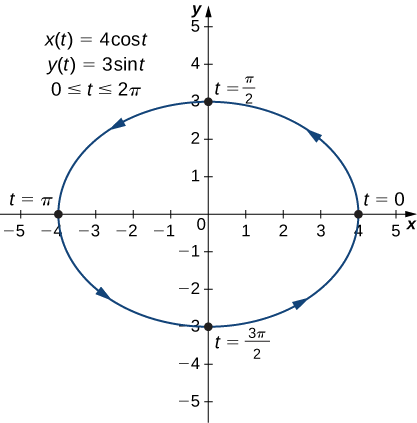
Коли t просувається від\(0\) до\(2π\), точка на кривій проходить еліпс один раз, у напрямку проти годинникової стрілки. Нагадаємо з розділу відкривачка, що орбіта Землі навколо Сонця також еліптична. Це прекрасний приклад використання параметризованих кривих для моделювання реального явища.
Виключіть параметр для плоской кривої, визначеної наступними параметричними рівняннями, і опишіть отриманий графік.
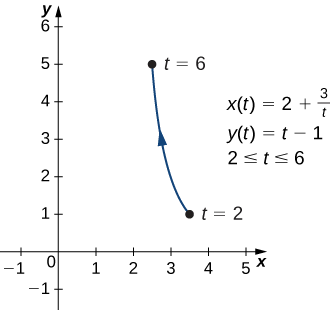
\[ x(t)=2+\dfrac{3}{t}, \quad y(t)=t−1, \quad\text{for }2≤t≤6 \nonumber \]
- Підказка
-
Розв'яжіть одне з рівнянь для\(t\) і підставляйте його в інше рівняння.
- Відповідь
-
\(x=2+\frac{3}{y+1},\)або\(y=−1+\frac{3}{x−2}\). Це рівняння описує частину прямокутної гіперболи з центром\((2,−1)\).
Поки ми бачили метод усунення параметра, припускаючи, що нам відомий набір параметричних рівнянь, які описують плоску криву. Що робити, якщо ми хотіли б почати з рівняння кривої і визначити пару параметричних рівнянь для цієї кривої? Це, безумовно, можливо, і насправді це можна зробити різними способами для заданої кривої. Процес відомий як параметризація кривої.
Знайдіть дві різні пари параметричних рівнянь для представлення графіка\(y=2x^2−3\).
Рішення
По-перше, завжди можна параметризувати криву\(x(t)=t\), визначаючи, а потім\(x\) замінивши на\(t\) в рівнянні для\(y(t)\). Це дає параметризацію
\[ x(t)=t, \quad y(t)=2t^2−3. \nonumber \]
Так як немає обмежень по домену в вихідному графіку, немає обмежень на значення\(t\).
Ми маємо повну свободу у виборі для другої параметризації. Наприклад, ми можемо вибрати\(x(t)=3t−2\). Єдине, що нам потрібно перевірити, це відсутність обмежень, що накладаються\(x\); тобто діапазон\(x(t)\) - це всі дійсні числа. Це справа для\(x(t)=3t−2\). Тепер\(y=2x^2−3\), з тих пір, ми можемо замінити\(x(t)=3t−2\)\(x\). Це дає
\[ y(t)=2(3t−2)^2−2=2(9t^2−12t+4)−2=18t^2−24t+8−2=18t^2−24t+6. \nonumber \]
Тому другу параметризацію кривої можна записати як
\( x(t)=3t−2\)і\( y(t)=18t^2−24t+6.\)
Знайдіть два різних набори параметричних рівнянь для представлення графіка\(y=x^2+2x\).
- Підказка
-
Дотримуйтесь інструкцій, описаних у прикладі\(\PageIndex{3}\). Пам'ятайте, що у нас є свобода у виборі параметризації для\(x(t)\).
- Відповідь
-
Одна можливість -\(x(t)=t, \quad y(t)=t^2+2t.\) Інша можливість\(x(t)=2t−3, \quad y(t)=(2t−3)^2+2(2t−3)=4t^2−8t+3.\) є Насправді існує нескінченна кількість можливостей.
Циклоїди та інші параметричні криві
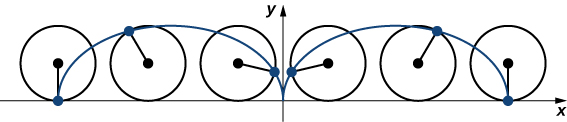
Уявіть, що їдете на велосипедну прогулянку по країні. Шини залишаються в контакті з дорогою і обертаються в передбачуваній схемі. Тепер припустимо, дуже рішучий мураха втомився після довгого дня і хоче повернутися додому. Так він висить на борт шини і отримує вільну їзду. Шляхом, яким проходить цей мураха по прямій дорозі, називається циклоїдом (рис.\( \PageIndex{8}\)). Циклоїда, породжена колом (або велосипедним колесом) радіусом a, задається параметричними рівняннями
\[x(t)=a(t−\sin t), \quad y(t)=a(1−\cos t).\nonumber \]
Щоб зрозуміти, чому це правда, розглянемо шлях, який займає центр колеса. Центр рухається уздовж\(x\) -осі на постійній висоті, рівній радіусу колеса. Якщо радіус є\(a\), то координати центру можна задати рівняннями
\[x(t)=at,\quad y(t)=a\nonumber \]
за будь-яке значення\(t\). Далі розглянемо мураха, який обертається навколо центру по круговій доріжці. Якщо велосипед рухається зліва направо, то колеса обертаються за годинниковою стрілкою. Можлива параметризація кругового руху мурашки (щодо центру колеса) задається
\[\begin{align*} x(t) &=−a \sin t \\[4pt] y(t) &=−a\cos t.\end{align*}\]
(Негативний знак потрібен, щоб змінити орієнтацію кривої. Якби негативного знака не було, нам довелося б уявити колесо, що обертається проти годинникової стрілки.) Додавання цих рівнянь разом дає рівняння для циклоїди.
\[\begin{align*} x(t) &=a(t−\sin t) \\[4pt] y(t) &=a(1−\cos t ) \end{align*}\]
Тепер припустимо, що колесо велосипеда не рухається по прямій дорозі, а замість цього рухається вздовж внутрішньої частини більшого колеса, як на малюнку\( \PageIndex{9}\). На цьому графіку зелене коло рухається навколо синього кола проти годинникової стрілки. Точка на краю зеленого кола простежує червоний графік, який називається гіпоциклоїдом.
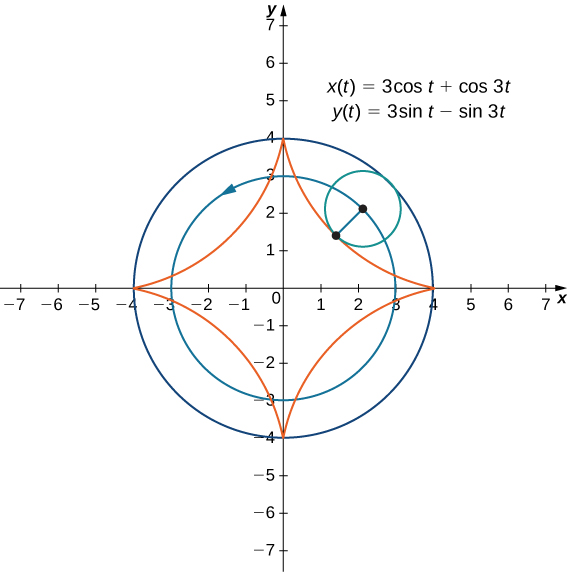
Загальні параметричні рівняння для гіпоциклоїди
\[x(t)=(a−b) \cos t+b \cos (\dfrac{a−b}{b})t \nonumber \]
\[y(t)=(a−b) \sin t−b \sin (\dfrac{a−b}{b})t. \nonumber \]
Ці рівняння трохи складніше, але виведення дещо схоже на рівняння для циклоїди. У цьому випадку ми припускаємо радіус більшого кола,\(a\) а радіус меншого кола дорівнює\(b\). Потім центр колеса рухається по колу радіуса\(a−b.\) Цей факт пояснює перший член у кожному рівнянні вище. Період другої тригонометричної функції в обох\(x(t)\) і\(y(t)\) дорівнює\(\dfrac{2πb}{a−b}\).
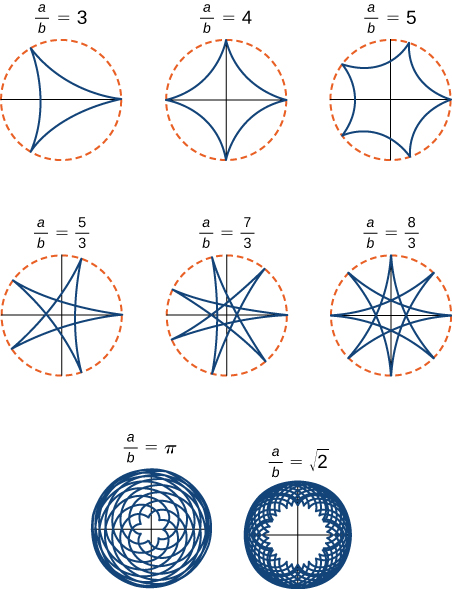
Співвідношення\(\dfrac{a}{b}\) пов'язане з кількістю стулок на графіку (кути - це кути або загострені кінці графіка), як показано на малюнку\( \PageIndex{10}\). Це співвідношення може привести до деяких дуже цікавих графіків, в залежності від того, чи є співвідношення раціональним. Цифра\(\PageIndex{9}\) відповідає\(a=4\) і\(b=1\). В результаті виходить гіпоциклоїд з чотирма стуками. На малюнку\(\PageIndex{10}\) показані деякі інші можливості. Останні два гіпоциклоїди мають ірраціональні значення для\(\dfrac{a}{b}\). У цих випадках гіпоциклоїди мають нескінченну кількість стуків, тому вони ніколи не повертаються до початкової точки. Це приклади того, що відомі як криві заповнення простору.
Багато плоских кривих в математиці названі на честь людей, які вперше досліджували їх, як фолій Декарта або спіраль Архімеда. Однак, мабуть, найдивніше ім'я кривої - відьма Агнесі. Чому відьма?
Марія Гаетана Агнезі (1718—1799) була однією з небагатьох визнаних жінок-математиків Італії вісімнадцятого століття. Вона написала популярну книгу з аналітичної геометрії, опубліковану в 1748 році, яка включала цікаву криву, яку вивчив Ферма в 1630 році. Математик Гвідо Гранді показав у 1703 році, як побудувати цю криву, яку він пізніше назвав «versoria», латинським терміном для мотузки, що використовується у вітрильному спорті. Агнесі використовувала італійський термін для цієї мотузки, «versiera», але в перекладі з латинської це ж слово означає «жіночий гоблін». Коли книга Агнесі була перекладена англійською мовою в 1801 році, перекладач використовував термін «відьма» для кривої, замість мотузки. Назва «відьма Агнесі» застрягла з тих пір.
Відьма Агнесі - це крива, визначена наступним чином: Почніть з кола радіуса a так, щоб точки\((0,0)\) і\((0,2a)\) були точками на колі (рис.\( \PageIndex{11}\)). Нехай O позначає походження. Виберіть будь-яку іншу точку А на колі, і проведіть січну лінію ОА. Нехай В позначають точку, в якій лінія ОА перетинає горизонтальну лінію наскрізь\((0,2a)\). Вертикальна лінія через B перетинає горизонтальну лінію через A в точці P. Оскільки точка А змінюється, шлях, який проходить точка Р, є відьмою кривої Агнесі для даного кола.
Криві відьми Агнесі мають застосування у фізиці, включаючи моделювання водних хвиль та розподіли спектральних ліній. У теорії ймовірностей крива описує функцію щільності ймовірності розподілу Коші. У цьому проекті ви будете параметризувати ці криві.
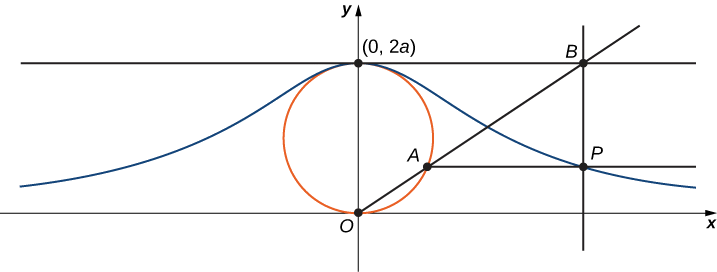
1. На малюнку намітьте наступні точки, довжини і кут:
a.\(C\) - точка на\(x\) -осі з тією ж\(x\) -координатою, що і\(A\).
b.\(x\)\(x\) - координата\(P\) та\(y\)\(y\) -координата\(P\).
в.\(E\) - це точка\((0,a)\).
d.\(F\) - точка на відрізку лінії\(OA\) така, щоб відрізок лінії був\(EF\) перпендикулярний відрізку лінії\(OA\).
е.\(b\) - відстань від\(O\) до\(F\).
f.\(c\) - відстань від\(F\) до\(A\).
г.\(d\) - відстань від\(O\) до\(C\).
h.\(θ\) - міра кута\(∠COA\).
Мета цього проекту - параметризувати відьму, використовуючи\(θ\) як параметр. Для цього потрібно написати рівняння для\(x\) і тільки\(y\) в терміні\(θ\).
2. Покажіть, що\(d=\dfrac{2a}{\sin θ}\).
3. Зауважте, що\(x=d\cos θ\). Покажіть, що\(x=2a\cot θ\). Коли ви це зробите, ви параметризуєте\(x\) -координату кривої щодо\(θ\). Якщо ви можете отримати подібне рівняння для\(y\), ви будете параметризувати криву.
4. З точки зору\(θ\), що таке кут\(∠EOA\)?
5. Покажіть, що\(b+c=2a\cos\left(\frac{π}{2}−θ\right)\).
6. Покажіть, що\(y=2a\cos\left(\frac{π}{2}−θ\right)\sin θ\).
7. Покажіть, що\(y=2a\sin^2θ\). Тепер ви параметризували\(y\) -координату кривої щодо\(θ\).
8. Зробіть висновок, що параметризація заданої кривої відьми
\[x=2a\cot θ, \quad y=2a \sin^2θ, \quad\text{for }−∞<θ<∞. \nonumber \]
9. Скористайтеся параметризацією, щоб показати, що задана крива відьми є графіком функції\(f(x)=\dfrac{8a^3}{x^2+4a^2}\).
Раніше в цьому розділі ми розглянули параметричні рівняння для циклоїди, яка є точкою шляху на краю слідів колеса, коли колесо котиться по прямому шляху. У цьому проекті ми розглянемо дві різні варіації циклоїди, які називаються циклоїдами куртату та пролату.
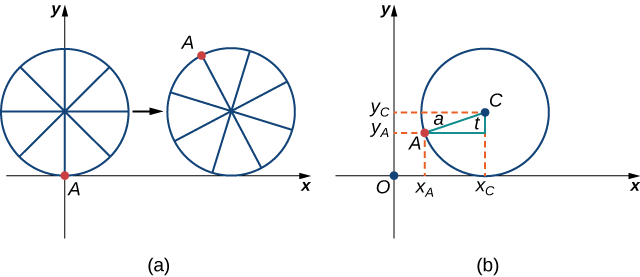
Для початку давайте повернемося до виведення параметричних рівнянь для циклоїди. Нагадаємо, що ми розглядали чіпкого мураха, який намагається дістатися додому, повісивши на край велосипедної шини. Ми припустили, що мураха забрався на шину у самого краю, де покришка торкається землі. У міру кочення колеса мураха рухається разом з краєм покришки (рис.\(\PageIndex{12}\)).
Як ми вже обговорювали, ми маємо велику гнучкість при параметризації кривої. У цьому випадку ми дозволяємо нашому параметру t представляти кут, через який шина оберталася. Дивлячись на малюнок\( \PageIndex{12}\), ми бачимо, що після того\(t\), як шина повернулася на кут, положення центру колеса\(C=(x_C,y_C)\), задається
\(x_C=at\)і\(y_C=a\).
Крім того,\(A=(x_A,y_A)\) дозволивши позначити положення мурашки, відзначимо, що
\(x_C−x_A=a\sin t\)і\(y_C−y_A=a \cos t\)
Тоді
\[x_A=x_C−a\sin t=at−a\sin t=a(t−\sin t) \nonumber \]
\[y_A=y_C−a\cos t=a−a\cos t=a(1−\cos t). \nonumber \]
Зверніть увагу, що це ті самі параметричні уявлення, які ми мали раніше, але тепер ми призначили фізичне значення параметричної змінної\(t\).
Через деякий час у мурашки паморочиться голова від обходу і округлення по краю шини. Так він піднімається вгору по одній зі спиць до центру колеса. Піднявшись до центру колеса, мураха змінив свій шлях руху. Новий шлях має менший рух вгору-вниз і називається куртатной циклоїдою (рис.\( \PageIndex{13}\)). Як показано на малюнку, давайте б позначимо відстань по спиці від центру колеса до мурашки. Як і раніше, ми дозволяємо t представляти кут, через який шина оберталася. Крім того, ми дозволяємо\(C=(x_C,y_C)\) представляти положення центру колеса і\(A=(x_A,y_A)\) представляємо положення мурашки.
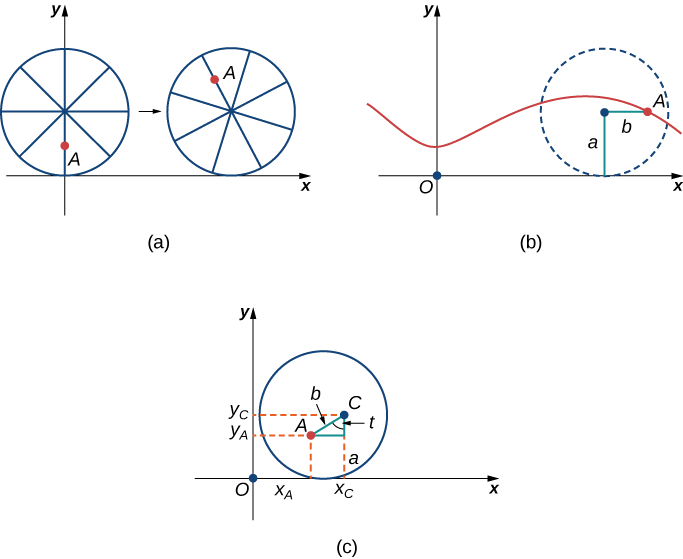
1. Яке положення центру колеса після повороту шини на кут\(t\)?
2. Використовуйте геометрію для пошуку виразів for\(x_C−x_A\) і for\(y_C−y_A\).
3. На основі ваших відповідей на частини 1 і 2, які параметричні рівняння представляють куртатний циклоїд?
Як тільки голова мурашки очищається, він розуміє, що велосипедист зробив поворот, і тепер їде далеко від свого будинку. Так він скидає з велосипедної шини і озирається навколо. На щастя, поруч є безліч залізничних колій, які прямують назад у правильному напрямку. Тож мураха прямує до залізничних колій, щоб чекати. Через деякий час проходить поїзд, прямуючи в потрібному напрямку, і йому вдається підстрибнути вгору і просто зловити край колеса поїзда (не розчавившись!).
Мураха все ще турбується про запаморочення, але колесо поїзда слизьке і не має спиць, щоб піднятися, тому він вирішує просто повісити на край колеса і сподіватися на краще. Тепер колеса поїзда мають фланець, щоб колесо працювало на коліях. Так, в даному випадку, оскільки мураха висить на самому краю фланця, відстань від центру колеса до мурашки фактично більше радіуса колеса (рис.\(\PageIndex{14}\)).
Налаштування тут по суті така ж, як коли мураха піднімався вгору по спиці на велосипедне колесо. Дозволяємо b позначити відстань від центру колеса до мурашки, і дамо t представляти кут, через який покришка оберталася. Додатково дозволимо\(C=(x_C,y_C)\) представляти положення центру колеса і\(A=(x_A,y_A)\) представляємо положення мурашки (рис.\( \PageIndex{14}\)).
Коли відстань від центру колеса до мурашки більше радіуса колеса, його шлях руху називається пролатной циклоїдою. Графік пролатного циклоїди показаний на малюнку.
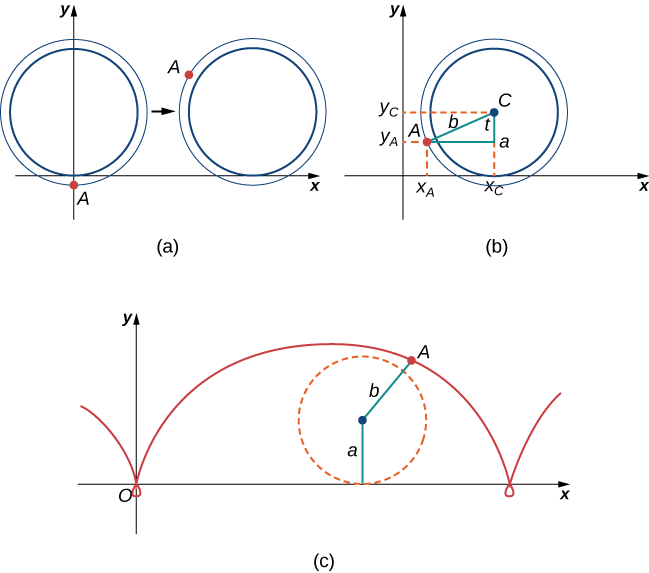
4. Використовуючи той же підхід, який ви використовували в частинок 1— 3, знайдіть параметричні рівняння для шляху руху мурашки.
5. Що ви помічаєте про свою відповідь на частину 3 та свою відповідь на частину 4?
Зверніть увагу, що мураха насправді рухається назад часом («петлі» на графіку), хоча поїзд продовжує рухатися вперед. Ймовірно, він буде дійсно запаморочливим до того часу, коли він повернеться додому!
Ключові концепції
- Параметричні рівняння забезпечують зручний спосіб опису кривої. Параметр може представляти час або якусь іншу значущу величину.
- Часто можна усунути параметр у параметризованій кривій, щоб отримати функцію або відношення, що описує цю криву.
- Завжди існує більше одного способу параметризації кривої.
- Параметричні рівняння можуть описувати складні криві, які важко або можливо неможливо описати за допомогою прямокутних координат.
Глосарій
- циклоїдний
- крива простежується точкою на обіді кругового колеса, коли колесо котиться по прямій лінії без прослизання
- куп
- загострений кінець або частина, де дві криві зустрічаються
- орієнтація
- напрямок, що точка рухається на графіку, як параметр збільшується
- параметр
- незалежна змінна, що обидва\(x\) і\(y\) залежать від параметричної кривої; зазвичай представлений змінною\(t\)
- параметрична крива
- графік параметричних рівнянь\(x(t)\) і\(y(t)\) над інтервалом у\(a≤t≤b\) поєднанні з рівняннями
- параметричні рівняння
- рівняння\(x=x(t)\) і\(y=y(t)\) які визначають параметричну криву
- параметризація кривої
- переписування рівняння кривої, визначеної функцією,\(y=f(x)\) як параметричні рівняння
