19.9: Циклоїдний маятник

Last updated
Save as PDF

Page ID: 76378

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Уявімо собі будівництво дерев'яної конструкції у формі циклоїди

альт

\[\begin{align} x &= a(2 \theta - \sin 2 \theta ) \label{19.9.1} \\[4pt] y &= 2a \cos ^2 \theta \label{19.9.2} \end{align} \]

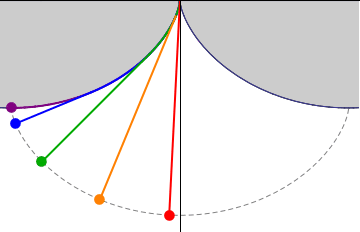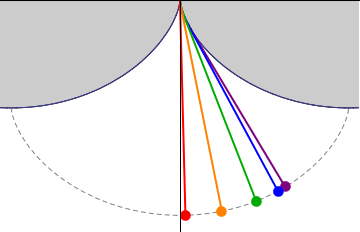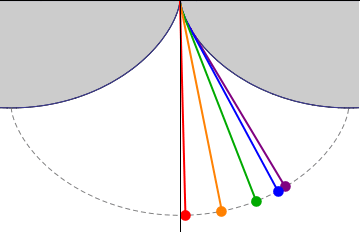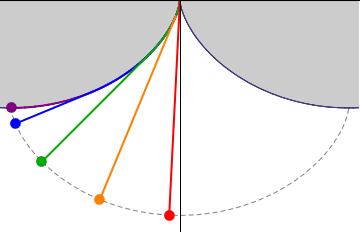
показаний товстою лінією на малюнку XIX.10. Тепер підвісьте маятник довжиною\(4a\) від чашок, і дайте йому розгойдуватися туди-сюди, частково обертаючись об дерев'яну раму так, як це робить. Якщо довжина дуги від зрізу до Р дорівнює\(s\), то довжина «вільної» струни дорівнює\(4a − s\), і тому координати боба на кінці маятника дорівнюють

\[ \begin{align} x &= a(2 \theta - \sin 2 \theta) + (4 a - s) \cos (180 ^\circ - \psi) \nonumber \\ &= a (2 \theta - \sin 2 \theta) + (4a - s) \sin \theta. \nonumber \end{align} \label{19.9.3} \]

\[\begin{align} y &= 2 a \cos^2 \theta - (4a - s) \sin (180 ^\circ - \psi) \nonumber \\&= 2 a \cos^2 \theta - (4a - s) \cos \theta \nonumber \end{align} \label{19.9.4} \]

(Вам потрібно буде нагадати собі точне значення,\(\psi\) а також використовувати Рівняння 19.4.20.) Тепер рівняння 19.4.18 говорить нам про те, що, і на заміну цього в рівняннях\( \ref{19.9.3} \) і\( \ref{19.9.4} \), ми знаходимо (після дуже невеликої алгебри і тригонометрії) для параметричних рівнянь до шляху, описаного боб маятника:

\[ x = a(2 \theta + \sin 2 \theta \label{19.9.5} \]

\[ y = -2 a \cos ^2 \theta. \label{19.9.6} \]

Таким чином, шлях маятникового боб (показаний у вигляді пунктирної лінії на малюнку XIX.10) є циклоїдою, а значить, його період не залежить від його амплітуди. (Нагадаємо, розділ 19.5.) При цьому маятник ізохронний або тавтохронний. Дивно дізнатися, що Гюйгенс побудував саме такий маятник ще в 1673 році.

Малюнок\(\PageIndex{1}\): П'ять ізохронних циклоїдних пендул з різною амплітудою. Всі вони ізохронні, тобто вони мають однакову частоту незалежно від їх амплітуди. Зверніть увагу на дві верхні циклоїдні дуги, які роблять боби описують циклоїдні траєкторії. (CC BY-SA 4.0; РЕМ088рой).