5.6: Деякі оцінки порядку величини

Last updated
Save as PDF

Page ID: 77805

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Як загальна пропозиція, обчислення оцінки фізичного ефекту на порядок вимагає розуміння 50% фізики, тоді як точний розрахунок вимагає близько 75%. ⁷ Ми досягли того моменту, коли розумно спробувати різноманітні оцінки порядку величини.

Примітка

Це твердження саме по собі є лише приблизною оцінкою. Той, хто викладав фізику, знає, що студенти часто обчислюють ефект точно, не розуміючи основної фізики взагалі.

Геодезичний ефект

Як ми могли експериментально підтвердити, що паралельний транспорт навколо замкнутого шляху може призвести до обертання вектора? Обертання пов'язане з кількістю кривизни простору/часу, що міститься в контурі, тому було б сенс вибрати петлю, що обертається навколо гравітаційного тіла. Ротація - це чисто релятивістський ефект, тому ми очікуємо, що він буде невеликим. Щоб його було легше виявити, ми повинні багато разів обходити цикл, викликаючи накопичення ефекту. Це, по суті, опис тіла, що обертається навколо іншого тіла. Очікується, що гіроскоп на борту орбітального тіла буде оброблятися. Це відоме як геодезичний ефект. У 1916 році, незабаром після того, як Ейнштейн опублікував загальну теорію відносності, Віллем де Ситтер розрахував вплив на систему земля-місяць. Ефект не був безпосередньо перевірений до 1980-х років, і перше високоточне вимірювання було в 2007 році, з аналізу результатів, зібраних супутниковим експериментом Gravity Probe B. Зонд мав чотири гіроскопи, виготовлені з кварцу, які були найдосконалішими сферами, коли-небудь виготовленими, варіюючись від сферичності не більше ніж на 40 атомів.

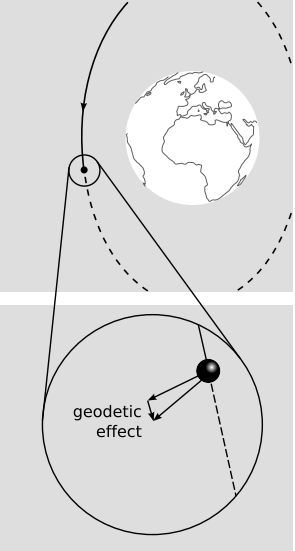
Малюнок 5.5.1.png — Малюнок\(\PageIndex{1}\) - Геодезичний ефект, виміряний гравітаційним зондом B.

Оцінимо розмір ефекту. Перша похідна метрики - це, приблизно, гравітаційне поле, тоді як друга похідна пов'язана з кривизною. Отже, кривизна простору-часу навколо Землі повинна змінюватися як ^{GmR −3}, де M - маса землі, а G - гравітаційна константа. Площа, укладена круговою орбітою, пропорційна r ², тому ми очікуємо, що геодезичний ефект буде змінюватися як\(\frac{nGM}{r}\), де n - кількість орбіт. Кут прецесії безмежний, і єдиний спосіб зробити цей результат безмежним - поставити в коефіцієнт\(\frac{1}{c^{2}}\). В одиницях з c = 1 цей коефіцієнт непотрібний. У звичайних метричних одиницях це має\(\frac{1}{c^{2}}\) сенс, оскільки це призводить до того, що чисто релятивістський ефект виходить малим. Результат, аж до безмежних факторів, які ми не претендували на те, щоб знайти, є

\[\Delta \theta \sim \frac{nGM}{c^{2} r} \ldotp\]

Ми також можемо очікувати прецесії Томаса. Як і ефект кривизни простору-часу, він був би пропорційним\(\frac{nGM}{c^{2} r}\). Оскільки ми не турбуємося про неодиничні фактори, ми можемо просто об'єднати прецесію Томаса разом з уже розрахованим ефектом.

Дані для гравітаційного зонда B складають r = r _e + (650 км) та n ≈ 5000 (обертаються на орбіті один раз на 90 хвилин протягом 353-денного періоду експерименту),\(\Delta \theta\) що дає 3 × 10 ⁻⁶ радіанів. На малюнку 5.5.2 показані фактичні результати ⁸ чотирьох гіроскопів на борту зонда. Прецесія становила близько 6 дугових секунд, або 3 × 10 ⁻⁵ радіанів. Наша сира оцінка була на правильному порядку. Відсутній безіменний коефіцієнт у правій частині рівняння вище дорівнює 3\(\pi\), що призводить два результати до досить тісного кількісного узгодження. Повне виведення, включаючи коефіцієнт 3\(\pi\), наведено в розділі 6.2.

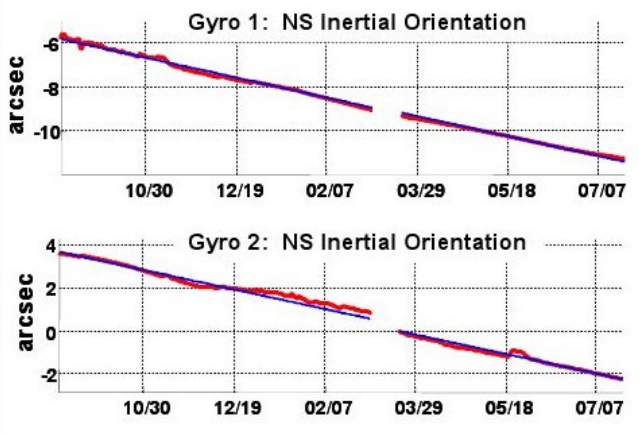
Малюнок 5.5.2a.png — Малюнок _5.5.2b.png» />

Малюнок\(\PageIndex{2}\) - Кут прецесії як функція часу, виміряний чотирма гіроскопами на борту гравітаційного зонда B.

Відхилення світлових променів

Під час обговорення вектора імпульсу чотири в розділі 4.2 ми побачили, що завдяки принципу еквівалентності на світло повинна впливати гравітація. Існує два шляхи, за допомогою яких такий ефект міг відбутися. Світло може набирати і втрачати імпульс, коли воно рухається вгору і вниз у гравітаційному полі, або його вектор імпульсу може відхилятися поперечним гравітаційним полем. Як приклад останнього, промінь зоряного світла може відхилятися гравітацією сонця, внаслідок чого видиме положення зірки на небі буде зміщено. Виявлення цього ефекту було одним з перших експериментальних тестів загальної теорії відносності. Зазвичай яскраве світло від сонця унеможливлювало б точно виміряти розташування зірки на небесній сфері, але цю проблему обійшов Артур Еддінгтон під час затемнення сонця в 1919 році.

Давайте оцінимо розмір цього ефекту. Ми вже бачили, що тензор Рімана - це, по суті, просто тензорний спосіб написання гаусової кривизни\(K = \frac{d \epsilon}{dA}\). Припустимо, заради цієї приблизної оцінки, що сонце, земля і зірка утворюють неевклідовий трикутник з прямим кутом біля Сонця. Тоді кутовий прогин збігається з кутовим дефектом\(\epsilon\) цього трикутника, і дорівнює інтегралу кривизни над внутрішньою частиною трикутника. Ігноруючи безодиничні константи, це закінчується точно таким же розрахунком, як і раніше, і результат полягає в тому\(\epsilon \sim \frac{GM}{c^{2} r}\), де r - відстань світлового променя найближчого наближення до сонця. Значення r не може бути меншим за радіус сонця, тому максимальний розмір ефекту знаходиться в порядку\(\frac{GM}{c^{2} r}\), де M - маса Сонця, і\(r\) є його радіусом. Знаходимо\(\epsilon\) 10 ⁻⁵ радіанів, або близько секунди дуги. Вимірювати положення зірки в межах дуги секунди було добре в межах сучасного стану в 1919 році, при хороших умовах в комфортній обсерваторії. Це спостереження, однак, вимагало, щоб команда Еддінгтона подорожувала на острів Прінсіпі, біля узбережжя Західної Африки. Погода була похмурою, і тільки протягом останніх 10 секунд семихвилинного затемнення небо було досить ясним, щоб дозволити знімати фотопластинки зоряного скупчення Гіад на тлі затемненого затемненого неба. Спостережуваний прогин становив 1,6 секунди дуги, згідно з релятивістським прогнозом. Релятивістське передбачення виведено в розділі 6.2.

Малюнок 5.5.3.png — Малюнок\(\PageIndex{3}\) - Одна з фотографій зі спостережень Еддінгтона за затемненням 1919 року. Це фотографічний негатив, тому коло, яке здається яскравим, насправді є темним обличчям Місяця, а темна область - це справді яскрава корона сонця. Зірки, позначені лініями над ними і під ними, з'являлися на позиціях, дещо інших, ніж їх нормальні, вказуючи на те, що їх світло було зігнуто гравітацією сонця на шляху до нашої планети.

Посилання

⁸ arxiv.org/абс/1105.3456