3.4: Моделі

Last updated
Save as PDF

Page ID: 77531

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Типова перша реакція на фразу «вигнутий простір-час» - або навіть «вигнутий простір», якщо на те пішло - це те, що це звучить як нісенітниця. Як може викривлятися або спотворюватися сам безликий, порожній простір? Поняття спотворення, здавалося б, передбачає взяття всіх точок і підштовхування їх у різних напрямках, як на картині Пікассо, щоб відстані між точками змінювалися. Але якщо простір не має ідентифікованих вм'ятин або подряпин, то, здавалося б, неможливо визначити, які старі точки були відправлені в які нові точки, і спотворення взагалі не матиме видимого ефекту. Чому ми повинні розраховувати на можливість будувати диференціальну геометрію на такому логічно сумнівному фундаменті? Дійсно, історично різні математики мали сильні сумніви щодо логічної самоузгодженості як неевклідової геометрії, так і нескінченності. І навіть якщо авторитетне джерело запевняє вас, що вийшла система самопослідовна, її загадкова і абстрактна природа, здавалося б, ускладнить вам розробку будь-якої робочої картини теорії, яка могла б зіграти ту роль, яку зіграють ментальні замальовки графіків в організації ваших знань про обчислення.

Малюнок 3.3.1.png — Малюнок\(\PageIndex{1}\) - Тулліо Леві-Чівіта (1873- 1941) працював над моделями систем числення, що володіють нескінченними величинами, і над диференціальною геометрією. Він винайшов тензорні позначення, які Ейнштейн дізнався зі свого підручника. Він був призначений на престижні наділені кафедри в Падуї та Римському університеті, але був звільнений у 1938 році, оскільки він був євреєм і антифашистом.

Моделі забезпечують спосіб вирішення як логічних, так і концептуальних питань. Малюнок 3.2.1 «вискакує» зі сторінки, представляючи сильне психологічне враження від криволінійної поверхні, винесеної в перспективі. Це передбачає знаходження фактичного математичного об'єкта, такого як криволінійна поверхня, яка задовольняє всім аксіомам певної логічної системи, наприклад неевклідової геометрії. Зверніть увагу, що модель може містити зовнішні елементи, такі як існування третього виміру, які не пов'язані з модельованою системою.

Давайте зосередимося спочатку на послідовності. Загалом, що вже говорити про самоузгодженість математичної системи? Для початку ми ніколи не можемо нічого довести про послідовність або відсутність послідовності чогось, що не є чітко визначеною формальною системою, наприклад, Біблією. Навіть елементи Евкліда, які були зразком формальної строгості протягом тисяч років, досить пухкі, щоб дозволити значну неоднозначність. Якщо ви схильні знущатися над дурними математиками Ренесансу, які продовжували намагатися довести паралельний постулат Е5 з постулатів Е1-Е4, розглянемо наступний аргумент. Припустимо, що ми замінюємо E5 на E5', який стверджує, що паралелей не існує: дана лінія і точка не на лінії, жодна лінія ніколи не може бути проведена через точку і паралельно заданій лінії. У новій системі плоскої геометрії E', що складається з E1-E4 плюс E5', ми можемо довести безліч теорем, і одна з них полягає в тому, що на площі будь-якої фігури існує верхня межа. Це накладає обмеження на розмір кіл, і це, здається, суперечить E3, який говорить, що ми можемо побудувати коло з будь-яким радіусом.

Тому ми робимо висновок, що E' не вистачає самоузгодженості. Упс! Як ваш текст геометрії середньої школи, безсумнівно, згадується мимохідь, E' є цілком респектабельною системою, яка називається еліптичною геометрією. Так що ж не так з цим передбачуваним доказом його відсутності самоузгодженості? Питання полягає в точному твердженні Е3. E3 не говорить, що ми можемо побудувати коло, задане будь-яке дійсне число як його радіус. Евклід не міг призначати жодного такого тлумачення, так як він не мав поняття про дійсні числа. Для Евкліда геометрія була первинною, а числа були геометрично побудованими об'єктами, представляючи як довжини, кути, площі та обсяги. Дослівний переклад висловлювання Евкліда аксіоми - «Описати коло з будь-яким центром і відстанню». ¹ «Відстань» означає відрізок лінії. Тому немає суперечності в E', тому що E' має обмеження на довжину відрізків лінії.

Тепер припустимо, що такі неясності були усунені з основних визначень і аксіом системи. Загалом, ми очікуємо, що буде простіше довести невідповідність непослідовної системи, ніж продемонструвати послідовність послідовної системи. У першому випадку ми можемо почати викручувати теореми, і якщо ми зможемо знайти спосіб довести як пропозицію P, так і його заперечення ¬P, то очевидно, що з системою щось не так. Можна задатися питанням, чи може таке протиріччя залишатися в одному кутку системи, як ядерні відходи. Арістотельська логіка допускає доказ протиріччям: якщо ми доведемо і P, і ¬P на основі певних припущень, то наші припущення, мабуть, були помилковими. Якщо ми можемо довести і P, і ¬P, не роблячи жодних припущень, то доказ протиріччям дозволяє встановити істинність будь-якого випадково обраного судження. Таким чином, єдиного протиріччя достатньо, в арістотелівської логіці, щоб визнати недійсною всю систему. Це йде латинською рубрикою ex falso quodlibet, що означає «від брехні, все, що вам заманеться». При цьому будь-яке протиріччя доводить невідповідність всієї системи.

Довести консистенцію важче. Якщо ви математично витончені, у вас може виникнути спокуса перейти безпосередньо до теореми Геделя і заявити, що ніхто ніколи не може довести самоузгодженість математичної системи. Це було б неправильним застосуванням Геделя. Теорема Геделя застосовується лише до математичних систем, які відповідають певним технічним критеріям, а деякі цікаві системи, з якими ми маємо справу, не відповідають цим критеріям; зокрема, теорема Геделя не застосовується до евклідової геометрії, а евклідова геометрія була доведена самоузгодженою Тарським та його студенти близько 1950 року. Крім того, ми зазвичай не вимагаємо абсолютного доказу самоузгодженості. Зазвичай ми задоволені, якщо можемо довести, що певна система, така як еліптична геометрія, принаймні така ж самоузгоджена, як інша система, наприклад евклідова геометрія. Це називається рівноузгодженістю. Загальна методика доведення рівновідповідності двох теорій полягає в тому, щоб показати, що модель однієї може бути побудована в межах іншої.

Припустимо, наприклад, що ми будуємо геометрію, в якій простір точок є поверхнею сфери, а лінії розуміються як геодезичні, тобто великі кола, центри яких збігаються в центрі сфери. Ця геометрія, звана сферичною геометрією, корисна в картографії та навігації. Це не евклідова, як ми можемо продемонструвати, виставляючи принаймні одну пропозицію, яка є помилковою в евклідовій геометрії. Наприклад, побудувати трикутник на земній поверхні з одним кутом на північному полюсі, а двома іншими на екваторі, розділеними 90 градусами довготи. Сума його внутрішніх кутів становить 270 градусів, що суперечить Евкліду, книга I, судження 32. Тому сферична геометрія повинна порушувати принаймні одну з аксіом E1-E5, і справді вона порушує як E1 (оскільки жодна унікальна лінія не визначається двома антиподальними точками, такими як північний та південний полюси) та E5 (оскільки паралелі взагалі не існують).

Тісно пов'язану конструкцію дає модель еліптичної геометрії, в якій тримається Е1, і за борт викидається тільки Е5. Для цього моделюємо точку, використовуючи діаметр сфери, ² і лінію як сукупність всіх діаметрів, що лежать в певній площині. Це має ефект виявлення антиподальних точок, так що зараз немає порушення Е1. Грубо кажучи, це схоже на відкидання половини сфери, але змушуючи краї обертатися навколо. Оскільки ця модель еліптичної геометрії закладена в евклідовому просторі, всі аксіоми еліптичної геометрії тепер можуть бути доведені як теореми евклідової геометрії. Якби з них виникло протиріччя, це означало б протиріччя в аксіомах евклідової геометрії. Зроблено висновок, що еліптична геометрія рівноузгоджується з евклідовою геометрією. Це було відомо задовго до доказу самоузгодженості евклідової геометрії Тарського 1950 року, але оскільки ніхто не втрачав сну через приховані протиріччя в евклідовій геометрії, математики перестали витрачати свій час на пошуки протиріч в еліптичній геометрії.

Примітка

Термін «еліптичний» може бути дещо оманливим тут. Модель все ще побудована з сфери, а не еліпсоїда.

Приклад 3: Нескінченність

Розглянемо наступну аксіоматично визначену систему чисел:

Це поле, тобто воно має додавання, віднімання, множення і ділення зі звичайними властивостями.
Це впорядкована геометрія в сенсі O1-O4, а впорядкування стосується додавання та множення звичайним способом.
Існування нескінченних чисел: Існує додатне число d таке, що d < 1, d < 1/2, d < 1/3,.

Модель цієї системи може бути побудована в межах дійсної системи числення шляхом визначення d як функції ідентичності d (x) = x і формування множини функцій виду f (d) = P (d) /Q (d), де P і Q є поліномами з дійсними коефіцієнтами. Порядок функцій f та g визначається за знаком\(\lim_{x \rightarrow 0^{+}}\) f (x) − g (x). Аксіоми 1-3 можуть бути доведені з аксіом дійсних чисел. Тому ця система, яка включає в себе нескінченнімалі, рівноузгоджується з реалами. Більш складні конструкції можуть поширювати це на системи, які мають більше властивостей реалів, а калькулятор на основі браузера, який реалізує таку систему, доступний за адресою lightandmatter.com/calc/inf. Авраам Робінсон розширив це в 1966 році на весь аналіз, і, таким чином, немає нічого суворо в тому, щоб робити аналіз у стилі Гаусса і Ейлера, з символами, такими як dx, що представляють нескінченно малі величини. ³

³ Детальніше про цю тему можна знайти в, наприклад, Елементарне обчислення Кейслера: нескінченно малий підхід, Короткий вступ Строяна до нескінченно малих обчислень або моє власне обчислення, всі з яких доступні безкоштовно в Інтернеті.

Окрім доведення послідовності, ці моделі дають нам уявлення про те, що відбувається. Модель еліптичної геометрії передбачає розуміння причини того, що існує верхня межа довжин і площ: це тому, що простір обертається навколо себе. Модель нескінченних чисел передбачає факт, який не відразу очевидний з аксіом: нескінченно малі величини складають ієрархію, так що, наприклад, 7d знаходиться в кінцевій пропорції d, тоді як d ² - як «менша блоха» у собачки Свіфта: «Великі блохи мають маленькі блохи/ На спині до їздити на них,/і маленькі блохи мають менше бліх, /І так, до нескінченності».

Сферична та еліптична геометрія не є дійсними моделями загальнорелятивістського просторового часу, оскільки вони локально евклідові, а не Лоренціанські, але вони все ще дають нам достатньо концептуальних вказівок, щоб придумати деякі ідеї, які ніколи не прийшли в голову нам інакше:

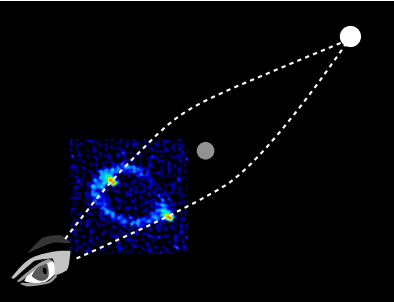
У сферичній геометрії ми можемо мати двосторонній багатокутник, який називається лінією, яка охоплює ненульову область. Загалом відносність, лінія, утворена світовими лініями двох частинок, являє собою рух, в якому частинки відокремлюються, але пізніше возз'єднуються, імовірно, через деяку масу між ними, яка створила гравітаційне поле. Прикладом може служити гравітаційне лінзування.
Обидві сферичні моделі обертаються навколо себе, так що вони не топологічно еквівалентні нескінченним площинам. Тому ми формуємо припущення, що може бути зв'язок між кривизною, яка є локальною властивістю, і топологією, яка є глобальною. Такий зв'язок дійсно спостерігається в теорії відносності. Наприклад, космологічні розв'язки рівнянь загальної відносності бувають двох смаків. Один тип має достатню кількість речовини в ньому, щоб виробляти більше певної критичної величини кривизни, і цей тип топологічно замкнутий. Він описує всесвіт, який має скінченний просторовий об'єм, і який буде існувати лише протягом кінцевого часу, перш ніж він повторюється у Big Crunch. Інший тип, відповідний Всесвіту, який ми насправді населяємо, має нескінченний просторовий об'єм, існуватиме нескінченний час і топологічно відкритий.
Існує шкала відстані, встановлена розміром сфери, причому її зворотна є мірою кривизни. Загалом відносність, ми очікуємо, що буде подібний спосіб вимірювання кривизни чисельно, хоча кривизна може змінюватися від точки до точки.

Малюнок 3.3.2.png — Малюнок\(\PageIndex{2}\) - Кільце Ейнштейна утворюється, коли є ймовірність вирівнювання далекого джерела з більш близьким гравітаційним тілом. Тут квазар, MG1131+0456, розглядається як кільце через фокусування світла невідомим об'єктом, можливо, надмасивною чорною дірою. Оскільки всьому розташуванню не вистачає ідеальної осьової симетрії, кільце неоднорідне; більша частина його яскравості зосереджена в двох грудочках з протилежних сторін. Цей тип гравітаційного лінзування є прямим доказом кривизни простору, передбаченої гравітаційним лінзуванням. Дві геодезики утворюють лінію, яка є фігурою, яка не може існувати в евклідовій геометрії.

Вправа\(\PageIndex{1}\)

Доведіть з аксіом E', що еліптична геометрія, на відміну від сферичної геометрії, не може мати лінію з двома різними вершинами. Переконайте себе тим не менш, використовуючи сферичну модель Е ', що можна в еліптичній геометрії для двох ліній обкласти область простору, в тому сенсі, що з будь-якої точки P в області промінь, випромінюваний в будь-якому напрямку, повинен перетинати одну з двох ліній. Узагальнити ці спостереження з характеристикою лун в еліптичній геометрії проти ліній у сферичній геометрії.

Посилання

¹ Хіт, с. 195-202