Skip to main content
LibreTexts - Ukrayinska

3: Інтеграли

  1. Last updated
  2. Save as PDF
  • Page ID
    79767

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

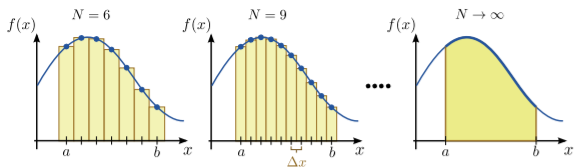
    Якщо у нас є функція,\(f(x)\) яка добре визначена для деяких\(a \le x \le b\), її інтеграл над цими двома значеннями визначається як\[\int_a^b dx\; f(x) \;=\; \lim_{N \rightarrow \infty} \, \sum_{n=0}^{N} \Delta x\; f(x_n) \;\;\;\mathrm{where}\;\; x_n = a + n\Delta x, \;\; \Delta x \equiv \left(\frac{b-a}{N}\right).\] Це називається певним інтегралом і представляє область під графом\(f(x)\) в області між \(x=a\)і\(x=b\), як показано на малюнку нижче. Функція\(f(x)\) називається цілим, а дві точки\(a\) і\(b\) називаються межами інтеграла. Інтервал між двома межами ділиться на\(N\) відрізки, довжиною\((b-a)/N\) кожен. Кожен член в сумі представляє площу прямокутника, а як\(N\rightarrow \infty\), сума сходиться до площі під кривою.

    clipboard_e7268f426693b00143c2821f372f5e056.png
    Малюнок\(\PageIndex{1}\)

    Множинний інтеграл передбачає інтеграцію більш ніж однієї змінної. Наприклад, коли у нас є функція,\(f(x_1,x_2)\) яка залежить від двох незалежних змінних,\(x_1\) і\(x_2\), ми можемо виконати подвійний інтеграл, інтегруючи спочатку одну змінну, потім іншу змінну:\[\int_{a_1}^{b_1} dx_1 \int_{a_2}^{b_2} dx_2 \; f(x_1, x_2) \equiv \int_{a_1}^{b_1} dx_1 F(x_1)\quad\text{where}\;\;F(x_1) \equiv \int_{a_2}^{b_2} dx_2 \; f(x_1, x_2).\]