3.5: Гауссова інтеграл

Ось відомий інтеграл:

$$\int_{-\infty}^\infty \; e^{-\gamma x^2} \; dx.$$ Integrand називається гаусова, або крива дзвінка, і зображена нижче. Чим більше значення$\gamma$, тим більш вузькопічна крива.

Малюнок$\PageIndex{1}$

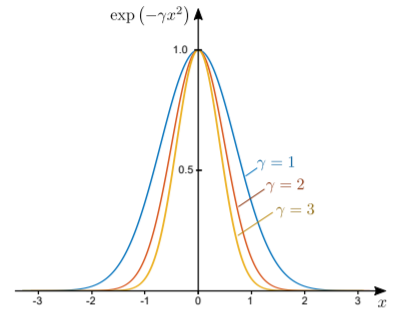
Інтеграл був вирішений Гауссом блискучим чином. $I(\gamma)$Дозвольте позначити значення інтеграла. Потім$I^2$ є лише дві незалежні копії інтеграла, помножені разом:

$$I^2(\gamma) = \left[\int_{-\infty}^\infty dx\; e^{-\gamma x^2}\right] \times \left[\int_{-\infty}^\infty dy\; e^{-\gamma y^2}\right].$$ Зверніть увагу, що у другій копії інтеграла ми змінили мітку «фіктивна»$x$ (змінна інтеграції) на$y$, щоб уникнути двозначності. Тепер це стає двовимірним інтегралом, взятим на всю площину 2D: $$I^2(\gamma) = \int_{-\infty}^\infty dx\, \int_{-\infty}^\infty dy \; e^{-\gamma (x^2+y^2)}.$$ Далі переходимо від декартових до полярних координат: $$I^2(\gamma) = \int_{0}^\infty dr\, r \int_{0}^{2\pi} d\phi \; e^{-\gamma r^2} = \left[ \int_{0}^\infty dr\, r \, e^{-\gamma r^2}\right] \times \left[\int_{0}^{2\pi} d\phi \right] = \frac{1}{2\gamma} \cdot 2\pi.$$ Беручи квадратний корінь, ми отримуємо результат $$I(\gamma) = \int_{-\infty}^\infty dx \; e^{-\gamma x^2} = \sqrt{\frac{\pi}{\gamma}}.$$