19.8: Скорочені та розширені циклоїди

Last updated
Save as PDF

Page ID: 76396

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

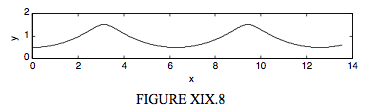
Як і в Розділі 19.1, ми вважаємо коло радіуса кочення вправо на прямій\(y = 2a\). Точка Р спочатку знаходиться нижче центру кола, але, замість того, щоб бути на обідку кола, її відстань від центру кола дорівнює\(r\). Якщо шлях\(r < a\), описаний P, буде скороченою циклоїдою; якщо\( r > a \), шлях є розширеною циклоїдою. (Я думаю, що є випадок використання цієї номенклатури навпаки, але більшість авторів, здається, використовують «контрактні» для\(r < a\) і «розширені» для\( r > a\).) Не повинно зайняти багато часу, щоб переконатися, аргументами, подібними до тих, що наведені в розділі 19.1, що параметричні рівняння до скороченої або розширеної циклоїди є

\[ x = 2 a \theta + r \sin 2 \theta \label{19.8.1}\tag{19.8.1} \]

\[ y = a - r \cos 2 \theta \label{19.8.2}\tag{19.8.2} \]

Вони проілюстровані на малюнках XIX.8 і XIX.9 для контрактної циклоїди з\(r = 0.5a\) і розширеної циклоїди с\(r = 1.5a\).

альт