19.10: Приклади циклоїдного руху у фізиці

На думку спадає кілька прикладів циклоїдного руху у фізиці. Одним з них є нутація вершини, яка описана в розділі 4.10 глави 10. Земна вісь нутує аналогічним чином. Іншим добре відомим прикладом є рух електрона в схрещених електричних і магнітних полах. Це описано в розділі 8 розділу «Електрика і магнетизм» цих нотаток. У космології, якщо середня щільність Всесвіту низька, Всесвіт розширюється до нескінченності, але, якщо щільність вище певної критичної щільності, то (безрозмірний) масштабний$R$ коефіцієнт Всесвіту розширюється і стискається з часом t відповідно до наступних параметричних циклоїдних рівнянь:

$$R = \dfrac{\Omega_0}{2(\Omega_0 -1) }(1 - \cos 2 \theta ) , \label{19.10.1}\tag{19.10.1}$$

$$t = \dfrac{\Omega_0}{2(\Omega_0 -1)^{3/2} }(2 \theta - \sin 2 \theta ). \label{19.10.2}\tag{19.10.2}$$

Тут$t$ виражається в одиницях зворотної нинішньої постійної Хаббла, і$\Omega_0$ є відношення нинішньої щільності Всесвіту до щільності, необхідної для «закриття» Всесвіту.

Менш відомий приклад стосується поширення звуку в атмосфері. У тропосфері, яка є нижньою частиною атмосфери приблизно до 11 км, температура знижується приблизно лінійно з висотою. У цьому випадку звук проходить через тропосферу циклоїдним шляхом. Швидкість звуку в газі пропорційна квадратному кореню температури. (Якщо вам цікаво, як це залежить від тиску Р і щільності$\rho$, відповідь полягає в тому, що воно залежить від співвідношення P/$\rho$ - і це співвідношення пропорційно температурі.) У будь-якому випадку, якщо температура знижується лінійно з висотою, швидкість звуку$v$ змінюється в залежності від висоти$y$ як

$$v = v_0 \sqrt{1 - cy} \label{19.10.3}\tag{19.10.3}$$

де c - константа, рівна приблизно 0,023 км ⁻¹ .Тепер, щоб простежити звуковий промінь через атмосферу, ми повинні зрозуміти, як змінюється напрямок поширення при проходженні звуку через шари повітря різної температури. Це регулюється, як і зі світлом, законом Снелла (див. Рис. XIX.11):

$$\dfrac{dv}{v} = - \tan \psi d \psi \label{19.10.4}\tag{19.10.4}$$

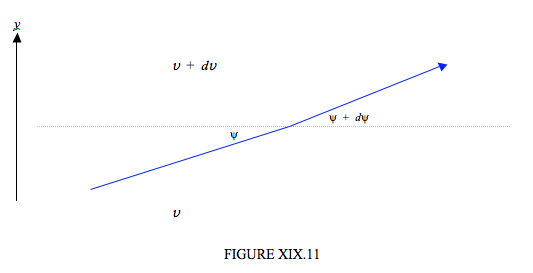
Закон Снелла стверджує, що коли звук (або світло) потрапляє в більш повільне середовище (тобто таке, в якому швидкість поширення повільніше), він згинається до норми. Я намалював малюнок XIX.11, щоб представити ситуацію в тропосфері, де температура (а отже, і швидкість звуку$v$) зменшується з висотою. Тобто,$dv/dy$ є негативним. Іншими словами, на$dv$ малюнку XIX є від'ємним, а Рівняння$\ref{19.10.4}$ вказує на те,$d\psi$ що позитивне, як намальовано. Якщо ви не визнаєте цю диференціальну форму закону Снелла, спробуйте інтегрувати її від$v_1$ до$v_2$ і від$\psi_1$ до$\psi_2$, і вона повинна припустити його більш звичну цілісну форму. Якщо тепер усунути$v$ між рівняннями$\ref{19.10.3}$ і$\ref{19.10.4}$, ви отримаєте диференціальне відношення між$y$ і$\psi$, яке, після інтеграції, стає

$$cy = 1 - \dfrac{\cos^2 \psi}{\cos^2 \psi_0} \label{19.10.5}\tag{19.10.5}$$

де$\psi_ 0$ - значення рівня землі$\psi$. Якщо ми введемо

$$a = \dfrac{1}{2c \cos ^2 \psi_0} , \label{19.10.6}\tag{19.10.6}$$

рівняння$\ref{19.10.5}$ можна зручно переписати

$$y = 2a(\sin^2 \psi - s\in^2 \psi_0) = 2a( \cos^2 \psi_0 - \cos^2 \psi \label{19.10.7}\tag{19.10.7}$$

Тепер$\tan \psi = dy/dx$, і усунення$y$ між цим і рівнянням$\ref{19.10.7}$ дасть диференціальне відношення між$x$ і$\psi$, яке, після інтеграції, стає

$$x = a[2(\psi - \psi_ 0 ) + \sin 2 \psi - \sin 2 \psi_0 ]. \label{19.10.8}\tag{19.10.8}$$

Рівняння$\ref{19.10.7}$ і$\ref{19.10.8}$ є параметричними рівняннями звукового шляху через тропосферу і описують циклоїду.

Вправа$\PageIndex{1}$: Problem for a Rainy Day

Якщо$x$ = 2,0 і$y$ = 1.6, то що таке$\psi$ і$\psi_0$?

Рішення

Я роблю це$\psi = 69 ^\circ, \psi_0 = 15 ^\circ 52'$.