2.20: Еліпси та еліпсоїди

Ось деякі проблеми, що стосуються еліпсів і еліпсоїдів, які можуть бути цікаві.

Визначають основні моменти інерції наступні:

1. Однорідна плоска пластинка маси\(m\) у вигляді еліпса півосей\(a \) і\( b\).
2. Однорідне плоске кільце маси\(m\) у вигляді еліпса півосей\(a \) і\( b\).
3. Однорідний твердий тривісний еліпсоїд маси\(m\)\(a, b \) і піввісь\( c\).
4. Рівномірний порожнистий тривісний еліпсоїд маси\(m\)\(a, b \) і піввісь\( c\).

1. За інтеграції еліптична пластинка трохи складна, але фізичним розумінням це дуже легко!

Розподіл маси навколо другорядної осі таке ж, як і для круглої пластинки радіуса\( a\), і тому момент\( B \) такий же, як і для круглої пластинки, а саме\( B = \frac{1}{4} ma^2 \). Аналогічно\( A = \frac{1}{4} mb^2 \), і, отже, по теоремі перпендикулярних осей,\(C = \frac{1}{4} m(a^2 + b^2 ) \).

Я думаю, ви виявите, що форма моментального еліпса така ж, як і форма оригінальної еліптичної ламіни.

2. Еліптичне кільце (обруч) - це надзвичайно складно. Він не може бути виражений елементарними функціями, і його доводиться обчислювати чисельно. Це може бути виражено через еліптичні інтеграли (не дивно), але більшість з нас не впевнені, що таке еліптичні інтеграли, і вони навряд чи вважаються елементарними функціями, і їх все одно доводиться обчислювати чисельно. Беремо еліпс, щоб бути\( \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1, \) с\( b≤a \).

Навіть обчислити окружність еліпса не так просто. Окружність дорівнює

\( \oint ds = 4 \int_{0}^{a} [ 1 + (\frac{dy}{dx} )^2] dx \), С\( y = b ( 1 - \frac{x^2}{a^2} )^\frac{1}{2} \).

Після трохи алгебри це можна записати як

\( \frac{4a}{x} \int_{0}^{a} \sqrt{\frac{c^2 -x^2}{a^2 - z^2}}dx \), де\( c^2 = \frac{a^4}{a^2 - b^2} \).

Спочатку це виглядає легко, але я не думаю, що ви можете це зробити в плані елементарних функцій. Немає проблем, тоді — просто інтегруйте його чисельно. На жаль, integrand стає нескінченним на верхній межі, тому все ще є трохи проблеми. Однак зміна змінної\( x = a \sin \theta \) вирішує цю проблему. Вираз для окружності стає просто

\( 4a\int_{0}^{\pi /2 } [1 - (\frac{a^2 - b^2}{a^2}) \sin ^2 \theta ]^\frac{1}{2} d \theta \),

які можуть бути інтегровані чисельно без проблем нескінченності на межі. За моїми розрахунками, окружність еліпса дорівнює\( ha \), де\(h\) є функція\(b/a \) наступним чином:

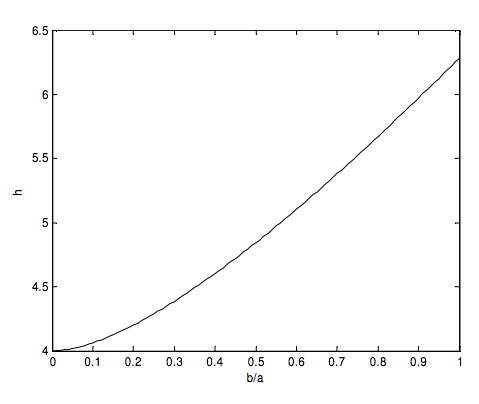
Щоб знайти момент інерції (або другий момент довжини) навколо другорядної осі, ми повинні помножити integrand на\(x^2 \), або\( a^2 \sin^2 \theta \), і інтегрувати. Таким чином, момент інерції еліптичного обруча навколо його другорядної осі знаходиться\(c_1ma^2 \), де

\ (c_1 =\ frac {\ int_ {0} ^ {\ pi/2} [1 - (\ frac {a^2 - b^2})\ sin^2\ тета] ^ {1/2}\ sin^2\ тета д
\ тета} {\ int_ {0} ^ {\ pi/2} [1- (\ frac {a^2 - b^2 2} {a^2})\ sin^2\ тета] ^ {1/2} д\ тета}\)

Момент інерції навколо великої осі є\(c_2ma^2 \), де

\( c_2 = \frac{ \frac{b^2}{a^2}\int_{0}^{\pi / 2 } [1 - ( \frac{a^2 - b^2}{a^2} ) cos^2]^{1/2} \sin^2 \theta d \theta }{ \int_{0}^{\pi / 2 } [ 1- (\frac{a^2 - b^2}{a^2} )\sin^2 \theta ]^{1/2} d \theta} \)

Ці два коефіцієнти\(ma^2 \) показані нижче як функція\(b/a \).

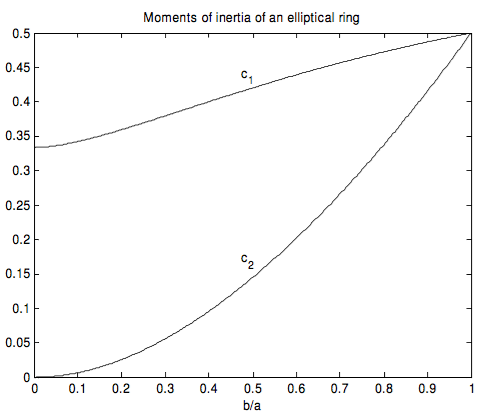
Моменти інерції еліптичного кільця маси\(m\) і напіввеликих і напівмалих осей\(a\) і\(b\) знаходяться\(c_1ma^2 \) навколо другорядної осі і\( c_2ma^2 \) навколо великої осі, де\(c_1 \) і\(c_2 \) показані як функції\(b/a \).

Момент інерції навколо великої осі також може бути зручно виражений в терміні,\( b \) а не\(a \). Якщо записати момент інерції близько великої осі як\(c_4mb^2\), то\(c_4 \) як функція\(b/a \) показана нижче.

Момент інерції навколо осі, перпендикулярної площині еліпса і проходить через його центр\(c_3ma^2 \), де, звичайно (по теоремі перпендикулярних осей),\( c_3 = c_1 + c_2 \).

Вона також дорівнює\( c_1ma^2 + c_4mb^2 \).

3. Для рівномірного твердого тривісного еліпсоїда моменти інерції складають

\( A = \frac{1}{5} m(b^2 + c^2) \qquad B = \frac{1}{5} m(c^2 + a^2) \qquad C = \frac{1}{5} m(c^2 + a^2) \)

Моментальний еліпсоїд не має однакової форми. Її осі знаходяться в співвідношенні

\( \)

Наприклад, якщо осьові відносини вихідного еліпсоїда складають 1:2: 3, осьові відносини відповідного моментального еліпсоїда є\( 1 : \sqrt{\frac{13}{10}} : \sqrt{\frac{13}{5}} = 1 : 1.140 : 1.612 \), який трохи більш сферичний, ніж вихідний еліпсоїд.

4. Тривісна еліптична оболонка. Доводиться добре подумати, що таке тривісна еліптична оболонка. Якщо уявити внутрішню поверхню оболонки еліпсоїдом, а зовнішню поверхню - аналогічним еліпсоїдом, але з усіма лінійними розмірами, збільшеними на той же малий дробовий приріст, то отримаємо цифру, подібну до такої:

На цьому кресленні лінійний розмір зовнішньої поверхні на 3 відсотки більше, ніж у внутрішньої поверхні. Е.Дж. Рут правильно показує в своєму трактаті про жорсткі тіла, що основними моментами інерції такої фігури є\( \frac{1}{3} m(b^2 + c^2), \frac{1}{3} m(c^2 + a^2), \frac{1}{3}m(a^2 + b^2) \).

Але видно, що така фігура не є (як імовірно м'яч рогера) рівномірної товщини. Намалюю нижче шкаралупу рівномірної товщини. У такому випадку внутрішня і зовнішня поверхні не зовсім схожі.

При спробі обчислити момент інерції такої цифри обмежуся випадком сфероїдальної оболонки рівномірної товщини. Тобто еліпсоїд з двома рівними осями, представлений рівнянням, в циліндричних координатах

\( \frac{\rho^2}{a^2} + \frac{z^2}{c^2} = 1, \)

де\( \rho^2 = x^2 + y^2 \). Далі, якщо поставити\( c = \chi a \), рівняння до сфероїду можна записати

\( \rho^2 + \frac{z^2}{\chi^2} = a^2, \)

Якщо\( \chi < 1 \), сфероїд сплющений. Якщо\( \chi > 1 \), сфероїд пролат.

Спочатку нам потрібно буде розрахувати його площу поверхні, яка дорівнює

\( A = 4 \pi \int_{0}^{c} \rho [ 1 + (\frac{d\rho}{dz})^2]^\frac{1}{2} dz \)

Після деякої алгебри це доходить до

\( A = 4 \pi a^2 f (\chi ), \)

де

\( f (\chi ) = \dfrac{1}{2}\left[\frac{\chi^2}{\sqrt{1 - \chi^2}} \ln \left( \dfrac{1 + \sqrt{1 - \chi^2}}{\chi}\right)+1\right] \)для\( \chi \leq 1 \)

і

\( f (\chi ) = \dfrac{1}{2}\left[\frac{\chi^2}{\sqrt{\chi^2-1}} \sin^{-1}\left( \dfrac{\sqrt{\chi^2-1}}{\chi}\right)+1\right]] \)для\( \chi \geq 1 \)

Ця функція показана нижче, наскільки\( \chi = 2 \). Для\( \chi = 0 \), фігура являє собою диск, загальна площа якого

(Верхня і нижня поверхня) є\(2 \pi a^2 \), і\( f = \frac{1}{2} \). Бо\( \chi = 1 \), фігура - це сфера, площа якої дорівнює\( 4 \pi a^2 \), і\( f = 1 \). Функція переходить до нескінченності, як\( \chi \) переходить до нескінченності.

Момент інерції навколо\(z\) -осі дорівнює

\( I = \frac{4 \pi m }{A}\int_{0}^{c} \rho ^3 [ 1 +(\frac{d \rho}{dz})^2]^{1/2} dz. \)

Після деякої алгебри це стає

\( I = ma^2 g ( \chi ) \)

\( g ( \chi ) = \frac{(2-\chi ^2) (1-\chi ^2) - \chi^4 \ln\left[\left(1 + \sqrt{1- \chi^2}\right)/ \chi\right]}{4 \left\{ (1- \chi^2)^{3/2} + \chi^2 (1-\chi^2) \ln\left[(1 + \sqrt{1- \chi^2})/ \chi \right]\right\} } \)для\( \chi \leq 1 \)

\( g (\chi) = 1 - \frac{\frac{\chi^4}{(\chi - 1)^{3/2}}sin^{-1}\left(\frac{\sqrt{\chi^2-1}}{\chi}\right)+\frac{\chi^2 -2}{\chi^2 -1 }}{4 \left\{ \frac{\chi^2}{\sqrt{\chi^2-1}}sin^{-1}\left(\frac{\sqrt{\chi^2-1}}{\chi}\right) +1 \right\}} \)для\( \chi \geq 1 \)

Ця функція показана нижче, наскільки\( \chi = 2 \) For\( \chi = 0 \), фігура являє собою диск, момент інерції якого дорівнює\( \frac{1}{2} \pi a^2 \), і\(f = \frac{1}{2} \). Бо\( \chi = 1 \), фігура являє собою порожнисту сферу, момент інерції якої дорівнює\( \frac{2}{3} \pi a^2 \), і\( f = \frac{2}{3} \). Функція переходить до 1, як\( \chi\) переходить до нескінченності; момент інерції наближається до моменту порожнистого циліндра.