12.6: Квадричні поверхні

Last updated
Save as PDF

Page ID: 61571

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Визначте циліндр як тип тривимірної поверхні.
Розпізнайте основні ознаки еліпсоїдів, параболоїдів та гіперболоїдів.
Використовуйте сліди, щоб намалювати перетину квадратних поверхонь з координатними площинами.

Ми вивчали вектори та векторні операції в тривимірному просторі і розробили рівняння для опису ліній, площин і сфер. У цьому розділі ми використовуємо наші знання про площини та сфери, які є прикладами тривимірних фігур, які називаються поверхнями, для дослідження безлічі інших поверхонь, які можуть бути побудовані у тривимірній системі координат.

Визначення циліндрів

Перша поверхня, яку ми розглянемо, - це циліндр. Хоча більшість людей відразу думають про порожнисту трубу або содову соломинку, коли чують слово циліндр, тут ми використовуємо широке математичне значення цього терміна. Як ми бачили, циліндричні поверхні не повинні бути круглими. Прямокутний нагрівальний канал являє собою циліндр, як і згорнутий килимок для йоги, перетин якого має спіральну форму.

У двовимірній координатній площині рівняння$ x^2+y^2=9$ описує коло, центрований у початку координат з радіусом$ 3$. У тривимірному просторі це ж рівняння являє собою поверхню. Уявіть собі копії кола, укладеного один на одного по центру на$z$ -осі (рис.$\PageIndex{1}$), утворюючи порожнисту трубку. Потім ми можемо побудувати циліндр з безлічі ліній, паралельних$z$ -осі, що проходять через коло$ x^2+y^2=9$ в$xy$ -площині, як показано на малюнку. Таким чином, будь-яка крива в одній з координатних площин може бути розширена, щоб стати поверхнею.

Ця цифра являє собою 3-мірну систему координат. Він має правий круглий центр з віссю z через центр. Циліндр також має точки, позначені на осі x і y в (3, 0, 0) і (0, 3, 0). — Малюнок$\PageIndex{1}$: У тривимірному просторі графік рівняння$ x^2+y^2=9$ являє собою циліндр з радіусом,$ 3$ центрованим на$z$ -осі. Триває нескінченно довго в позитивному і негативному напрямках.

Визначення: циліндри та постанови

Набір ліній, паралельних заданій лінії, що проходять через задану криву, відомий як циліндрична поверхня, або циліндр. Паралельні лінії називаються постановами.

З цього визначення ми бачимо, що у нас все ще є циліндр у тривимірному просторі, навіть якщо крива не є колом. Будь-яка крива може утворювати циліндр, а постанови, що складають циліндр, можуть бути паралельні будь-якій заданій лінії (рис.$\PageIndex{2}$).

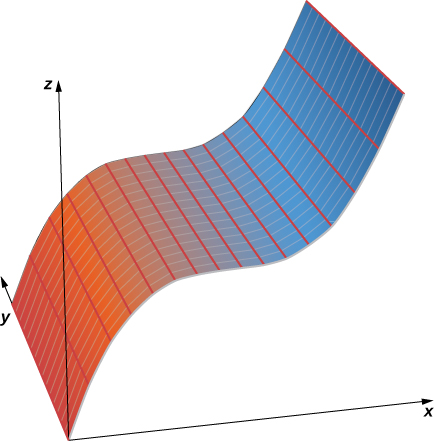
Ця фігура має 3-мірну поверхню, яка починається на осі Y і вигинається вгору. Також є мічені осі x і z. — Малюнок$\PageIndex{2}$: У тривимірному просторі графік рівняння$ z=x^3$ являє собою циліндр, або циліндричну поверхню з правилами, паралельними$y$ -осі.

Приклад$ \PageIndex{1}$: Graphing Cylindrical Surfaces

Намалюйте графіки наступних циліндричних поверхонь.

$ x^2+z^2=25$
$ z=2x^2−y$
$ y=\sin x$

Рішення

а Змінна$ y$ може приймати будь-яке значення без обмежень. Тому лінії, що правлять цією поверхнею, паралельні$y$ -осі. Перетин цієї поверхні з$xz$ -площиною утворює окружність, центровану у початку координат з радіусом$ 5$ (див. Рис.$\PageIndex{3}$).

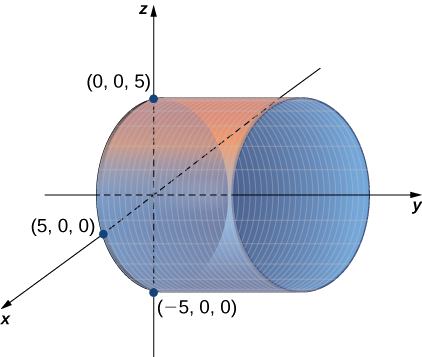
Ця цифра є 3-мірною системою координат. Він має правий круглий циліндр на боці з віссю y в центрі. Циліндр перетинає вісь x в (5, 0, 0). Він також має дві точки перетину, позначені на осі z в (0, 0, 5) і (0, 0, -5). — Малюнок$\PageIndex{3}$: Графік рівняння$ x^2+z^2=25$ являє собою циліндр з радіусом,$ 5$ центрованим на$y$ -осі.

b У цьому випадку рівняння містить усі три змінні —$ x,y,$ і$ z$ — тому жодна зі змінних не може змінюватися довільно. Найпростіший спосіб візуалізації цієї поверхні - скористатися комп'ютерною графічною утилітою (рис.$\PageIndex{4}$).

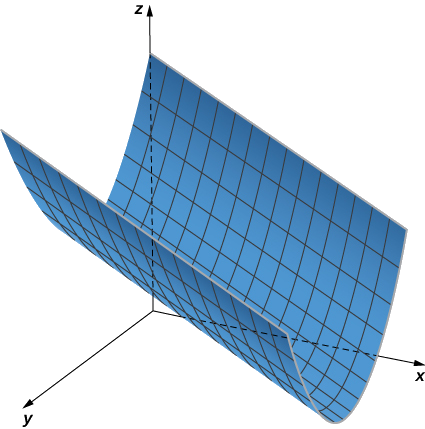
Ця цифра має поверхню в першому октанті. Перетин твердого тіла - парабола. — Малюнок$\PageIndex{4}$

c У цьому рівнянні змінна$ z$ може приймати будь-яке значення без обмеження. Тому лінії, що складають цю поверхню, паралельні$z$ -осі. Перетин цієї поверхні з xy -площиною обводить криву$ y=\sin x$ (рис.$\PageIndex{5}$).

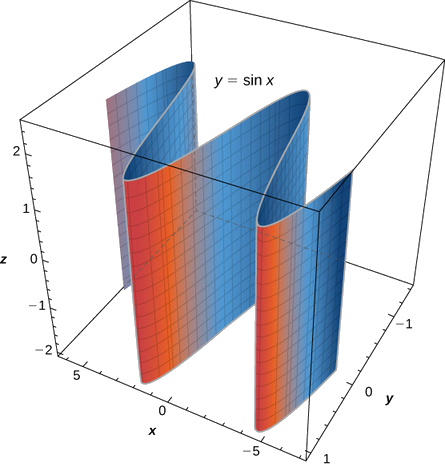
Ця цифра являє собою тривимірну поверхню. Поперечний переріз поверхні, паралельної площині x y, буде синусоїдною кривою. — Малюнок$\PageIndex{5}$: Графік рівняння$ y=\sin x$ утворений сукупністю ліній, паралельних$z$ осі -осі, що проходять через криву$ y=\sin x$ в$xy$ -площині.

Вправа$ \PageIndex{1}$:

Намалюйте або скористайтеся графічним інструментом для перегляду графіка циліндричної поверхні, визначеної рівнянням$ z=y^2$.

Підказка: Змінна$ x$ може приймати будь-яке значення без обмеження.
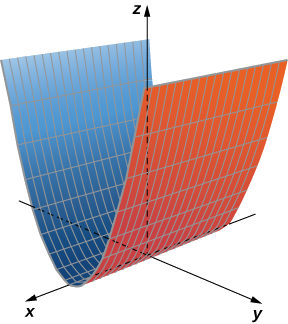
Відповідь: $Ця цифра є поверхнею над площиною x y. Поперечний переріз цієї поверхні паралельно площині y z був би параболою. Поверхня знаходиться на вершині площини x y.$

Під час ескізу поверхонь ми бачили, що корисно накидати перетин поверхні з площиною, паралельною одній з координатних площин. Ці криві називаються слідами. Їх ми можемо побачити на сюжеті циліндра на рис$\PageIndex{6}$.

Визначення: сліди

Сліди поверхні - це поперечні перерізи, створені, коли поверхня перетинає площину, паралельну одній з координатних площин.

Сліди корисні для ескізів циліндричних поверхонь. Однак для циліндра в трьох вимірах знадобиться лише один набір слідів. Зверніть увагу, на малюнку$\PageIndex{6}$, що слід графа$ z=\sin x$ в xz -площині корисний при побудові графіка. Слід в xy -площині, однак, є лише серією паралельних ліній, а слід в yz -площині просто одна лінія.

Ця цифра має два зображення. Перше зображення - це поверхня. Поперечний переріз поверхні, паралельної площині x z, буде синусоїдною кривою. Друге зображення - крива синуса в площині x y. — Малюнок$\PageIndex{6}$: (а) Це один вид графіка рівняння$ z=\sin x$. (b) Щоб знайти слід графа в$xz$ -площині, встановити$ y=0$. Слід - це просто двовимірна синусоїда.

Циліндричні поверхні утворені сукупністю паралельних ліній. Однак не всі поверхні в трьох вимірах побудовані так просто. Зараз ми досліджуємо більш складні поверхні, і сліди є важливим інструментом у цьому дослідженні.

Квадричні поверхні

Ми дізналися про поверхні в трьох вимірах, описаних рівняннями першого порядку; це площини. Деякі інші поширені типи поверхонь можна описати рівняннями другого порядку. Ми можемо розглядати ці поверхні як тривимірні розширення конічних перерізів, про які ми говорили раніше: еліпса, параболи та гіперболи. Ми називаємо ці графіки квадратними поверхнями.

Визначення: Квадричні поверхні та конічні перерізи

Квадричні поверхні - це графіки рівнянь, які можуть бути виражені у вигляді

\[Ax^2+By^2+Cz^2+Dxy+Exz+Fyz+Gx+Hy+Jz+K=0. \nonumber \]

Коли квадратна поверхня перетинає координатну площину, слід є конічним перерізом.

Еліпсоїд - це поверхня, описана рівнянням форми$ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}=1.$ Set,$ x=0$ щоб побачити слід еліпсоїда в yz -площині. Побачити сліди в$xy$ - і$xz$ -площині, встановлюють$ z=0$ і$ y=0$, відповідно. Зверніть увагу, що$ a=b$, якщо, слід в$xy$ -площині - це коло. Аналогічно$ a=c$, якщо, слід в$xz$ -площині - це коло і$ b=c$, якщо, то слід в$yz$ -площині - це коло. Тоді сфера - це еліпсоїд з$ a=b=c.$

Приклад$ \PageIndex{2}$: Sketching an Ellipsoid

Ескіз еліпсоїда

\[ \dfrac{x^2}{2^2}+\dfrac{y^2}{3^2}+\dfrac{z^2}{5^2}=1. \nonumber \]

Рішення

Почніть з ескізу слідів. Щоб знайти слід в xy -площині, встановлюємо$ z=0: \dfrac{x^2}{2^2}+\dfrac{y^2}{3^2}=1$ (рис.$\PageIndex{7}$). Щоб знайти інші сліди, спочатку встановити,$ y=0$ а потім встановити$ x=0.$

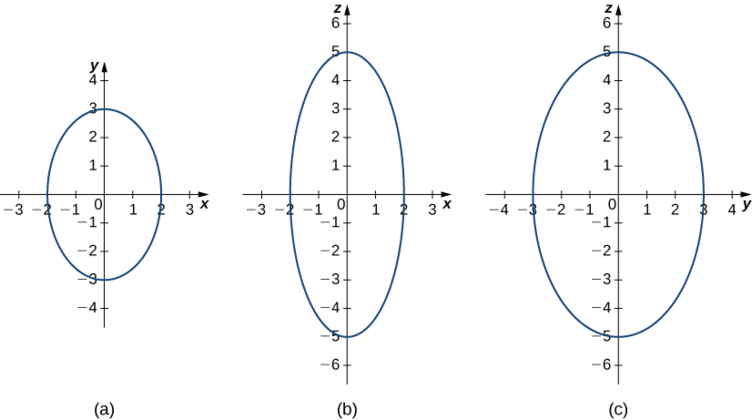
Ця цифра має три зображення. Перше зображення являє собою овал з центром навколо початку прямокутної системи координат. Він перетинає вісь x на -2 і 2. Він перетинає вісь Y на -3 і 3. Друге зображення являє собою овал з центром навколо початку прямокутної системи координат. Він перетинає вісь x на -2 і 2 і вісь y на -5 і 5. Третє зображення являє собою овал з центром навколо початку прямокутної системи координат. Він перетинає вісь x на -3 і 3 і осі y на -5 і 5. — Рисунок$\PageIndex{7}$: (a) Цей графік представляє слід рівняння$ \dfrac{x^2}{2^2}+\dfrac{y^2}{3^2}+\dfrac{z^2}{5^2}=1$ в$xy$ -площині, коли ми встановимо$ z=0$. (b) Коли ми встановимо$ y=0$, ми отримуємо слід еліпсоїда в$xz$ -площині, яка є еліпсом. (c) Коли ми встановимо$ x=0$, ми отримуємо слід еліпсоїда в$yz$ -площині, який також є еліпсом.

Тепер, коли ми знаємо, як виглядають сліди цього твердого тіла, ми можемо накидати поверхню в трьох вимірах (рис.$\PageIndex{8}$).

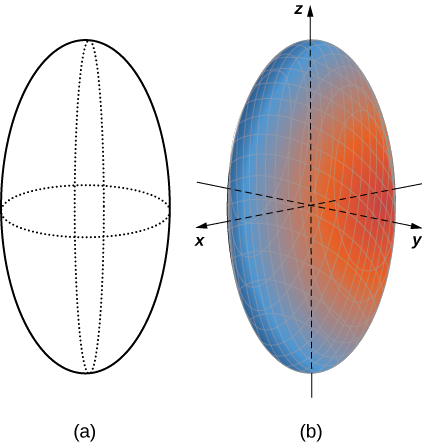
Ця цифра має два зображення. Перше зображення являє собою вертикальний еліпс. Там дві криві, намальовані пунктирними лініями навколо центру по горизонталі і вертикалі, щоб надати зображенню 3-мірну форму. Друге зображення являє собою суцільну еліптичну форму з центром у початку 3-мірної системи координат. — Малюнок$\PageIndex{8}$: (а) Сліди забезпечують основу для поверхні. (б) Центр цього еліпсоїда є початком.

Слід еліпсоїда - це еліпс у кожній з координатних площин. Однак це не обов'язково має бути для всіх квадратних поверхонь. Багато чотирикутні поверхні мають сліди, які представляють собою різні види конічних перерізів, і це зазвичай позначається назвою поверхні. Наприклад, якщо поверхня може бути описана рівнянням форми

\[ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=\dfrac{z}{c} \nonumber \]

то ми називаємо цю поверхню еліптичним параболоїдом. Слід в xy -площині є еліпсом, але сліди в xz- площині і yz -площині є параболами (рис.$\PageIndex{9}$). Інші еліптичні параболоїди можуть мати інші орієнтації, просто змінюючи змінні, щоб дати нам іншу змінну в лінійному члені рівняння$ \dfrac{x^2}{a^2}+\dfrac{z^2}{c^2}=\dfrac{y}{b}$ або$ \dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}=\dfrac{x}{a}$.

Ця цифра є зображенням поверхні. Він знаходиться в 3-вимірній системі координат поверх початку. Поперечний переріз цієї поверхні, паралельної площині x y, буде еліпсом. — Малюнок$\PageIndex{9}$: Ця квадратна поверхня називається еліптичним параболоїдом.

Приклад$ \PageIndex{3}$: Identifying Traces of Quadric Surfaces

Опишіть сліди еліптичного параболоїда$ x^2+\dfrac{y^2}{2^2}=\dfrac{z}{5}$.

Рішення

Щоб знайти слід в$xy$ -площині,$ z=0: x^2+\dfrac{y^2}{2^2}=0.$ встановіть слід в площині просто$ z=0$ одна точка, початок. Оскільки одна точка не говорить нам, що таке форма, ми можемо рухатися вгору по$z$ -осі до довільної площини, щоб знайти форму інших слідів фігури.

Слід в площині$ z=5$ - це графік рівняння$ x^2+\dfrac{y^2}{2^2}=1$, який є еліпсом. У$xz$ -площині рівняння стає$ z=5x^2$. Слід - це парабола в цій площині і в будь-якій площині з рівнянням$ y=b$.

У площині, паралельних$yz$ -площині, сліди також є параболами, як ми бачимо на малюнку$\PageIndex{10}$.

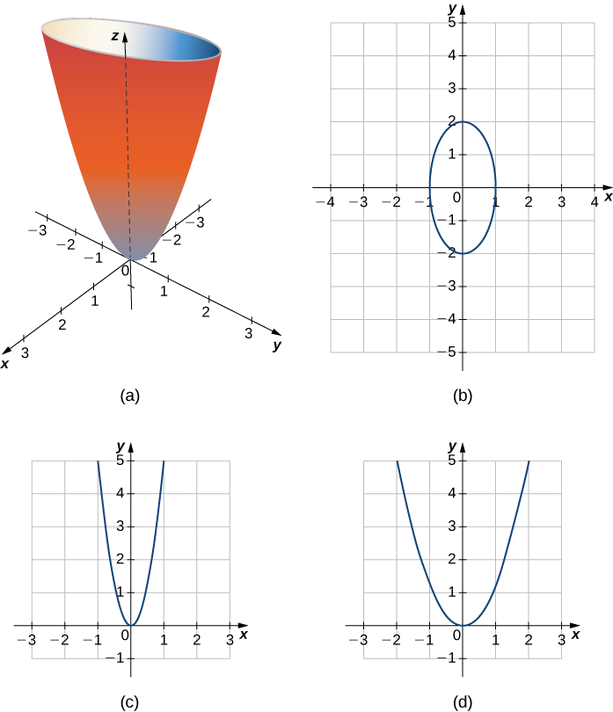
Ця цифра має чотири зображення. Перше зображення - це зображення поверхні. Він знаходиться в 3-вимірній системі координат поверх початку. Поперечний переріз цієї поверхні, паралельної площині x y, буде еліпсом. Поперечний переріз, паралельний площині x z, буде параболою. Поперечний переріз поверхні, паралельної площині y z, буде параболою. Друге зображення є поперечним перерізом, паралельним площині x y і являє собою еліпс. Третє зображення - це поперечний переріз паралельно площині x z і є параболою. Четверте зображення - це поперечний переріз паралельно площині y z і є параболою. — Малюнок$\PageIndex{10}$: (а) Параболоїд$ x^2+\dfrac{y^2}{2^2}=\dfrac{z}{5}$. (б) Слід в площині$ z=5$. (c) Слід в$xz$ -площині. (d) Слід в$yz$ -площині.

Вправа$ \PageIndex{2}$:

Гіперболоїд одного листа - це будь-яка поверхня, яку можна описати рівнянням форми$ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1$. Опишіть сліди гіперболоїда одного листа, заданого рівнянням$ \dfrac{x^2}{3^2}+\dfrac{y^2}{2^2}−\dfrac{z^2}{5^2}=1.$

Підказка

Щоб знайти сліди в координатних площинях, задайте кожній змінній нуль окремо.

Відповідь

Сліди, паралельні$xy$ -площині, є еліпсами, а сліди паралельні$xz$ - і$yz$ -площинам - гіперболами. Зокрема, слід в$xy$ -площині еліпс$ \dfrac{x^2}{3^2}+\dfrac{y^2}{2^2}=1,$ слід в$xz$ -площині гіпербола,$ \dfrac{x^2}{3^2}−\dfrac{z^2}{5^2}=1,$ а слід в$yz$ -площині гіпербола$ \dfrac{y^2}{2^2}−\dfrac{z^2}{5^2}=1$ (див. Наступний малюнок).

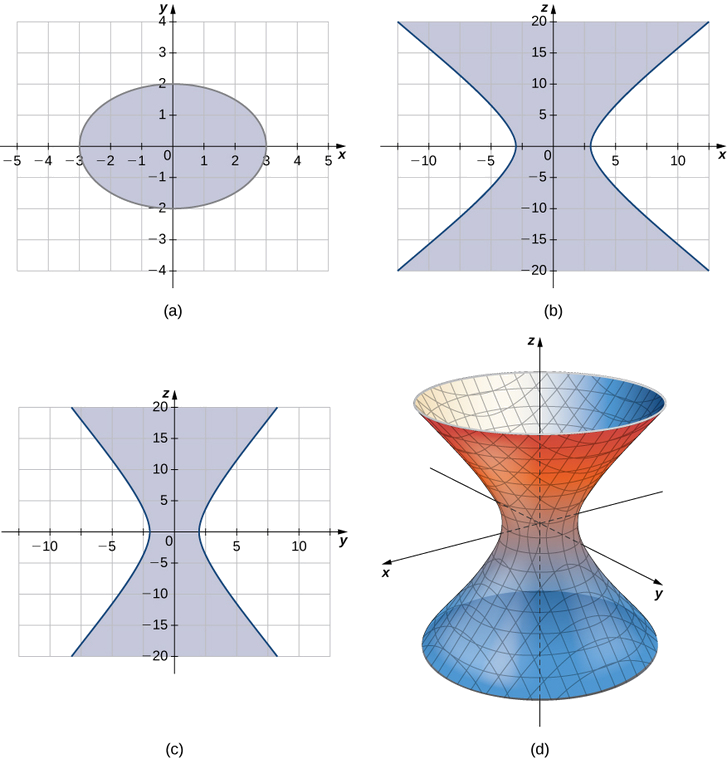
$Ця цифра має чотири зображення. Перше зображення являє собою еліпс з центром у початковій точці прямокутної системи координат. Вона перетинає вісь х на -3 і 3. Він перетинає вісь y на -2 і 2. Друге зображення - це графік гіперболи. Це дві криві, що відкриваються у негативному напрямку x, а симетрична - у позитивному напрямку x. Третє зображення - це графік гіперболи в площині y z. Це відкриття в негативному напрямку y і симетрична крива, що відкривається в позитивному напрямку y. Четверте зображення являє собою 3-мірну поверхню. Це верхнє і нижнє поперечні перерізи були б круговими. Вертикальний перетин буде гіперболою.$

Гіперболоїди одного листа мають деякі захоплюючі властивості. Наприклад, вони можуть бути побудовані за допомогою прямих ліній, таких як у скульптурі на малюнку$\PageIndex{11a}$. Насправді градирні для атомних електростанцій часто споруджуються у формі гіперболоїда. Будівельники мають можливість використовувати в будівництві прямі сталеві балки, що робить вежі дуже міцними при використанні відносно невеликого матеріалу (рис.$\PageIndex{11b}$).

Ця цифра має два зображення. Перше зображення являє собою скульптуру, виконану з паралельних паличок, зігнутих між собою по колу з гіперболічним перетином. Друге зображення - атомна електростанція. Вежі мають гіперболічну форму. — Малюнок$\PageIndex{11}$: (а) Скульптура у формі гіперболоїда може бути побудована з прямих ліній. (б) Градирні для атомних електростанцій часто будуються у формі гіперболоїда.

Приклад$ \PageIndex{4}$: Chapter Opener: Finding the Focus of a Parabolic Reflector

Енергія, що потрапляє на поверхню параболічного відбивача, зосереджена в фокусній точці відбивача (рис.$\PageIndex{12}$). Якщо поверхня параболічного відбивача описана рівнянням,$ \dfrac{x^2}{100}+\dfrac{y^2}{100}=\dfrac{z}{4},$ де знаходиться фокусна точка рефлектора?

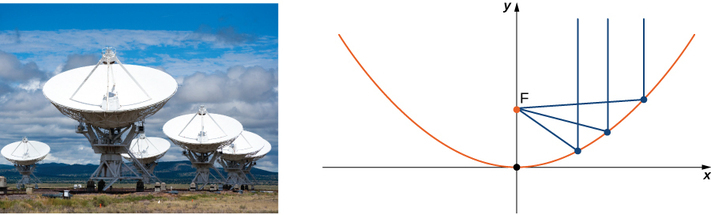
Ця цифра має два зображення. Перше зображення являє собою знімок супутникових антен з параболічними відбивачами. Друге зображення - параболічна крива на відрізку лінії. Дно кривої знаходиться в точці V. Є відрізок лінії, перпендикулярний іншому відрізку лінії через V. На цьому відрізку лінії є точка з позначенням F. Є 3 лінії від F до параболи, що перетинаються на P sub 1, P sub 2 і P sub 3. Є також три вертикальні лінії від P sub 1 до Q sub 1, від P sub 2 до Q sub 2, і від P sub 3 до Q sub 3. — Малюнок$\PageIndex{12}$: Енергія відбивається від параболічного відбивача і збирається в фокусній точці. (кредит: модифікація CGP Grey, Wikimedia Commons)

Рішення

Оскільки z - змінна першої потужності, то вісь відбивача відповідає$z$ вісь -осі. Коефіцієнти$ x^2$ and $ y^2$ are equal, so the cross-section of the paraboloid perpendicular to the $z$ -осі - це коло. Ми можемо розглянути слід в xz -площині або yz -площині; результат той же. Встановлення$ y=0$, the trace is a parabola opening up along the $z$ -axis, зі стандартним рівнянням$ x^2=4pz$, where $ p$ is the focal length of the parabola. In this case, this equation becomes $ x^2=100⋅\dfrac{z}{4}=4pz$ or $ 25=4p$. So p is $ 6.25$ m, which tells us that the focus of the paraboloid is $ 6.25$ m up the axis from the vertex. Because the vertex of this surface is the origin, the focal point is $ (0,0,6.25).$

Сімнадцять стандартних квадратних поверхонь можна вивести із загального рівняння

\[Ax^2+By^2+Cz^2+Dxy+Exz+Fyz+Gx+Hy+Jz+K=0. \nonumber \]

Наступні цифри підсумовують найважливіші з них.

Ця цифра являє собою таблицю з двома стовпцями і трьома рядками. Три ряди представляють перші 6 квадратних поверхонь: еліпсоїд, гіперболоїд одного листа і гіперболоїд з двох аркушів. Рівняння і сліди знаходяться в першій колонці. Другий стовпець містить графіки поверхонь. Еліпсоїдний графік являє собою вертикальну довгасту круглу форму. Гіперболоїд одного листа круглий зверху і знизу і вузький посередині. Гіперболоїд в двох листах має два параболічних купола навпроти один одного. — Малюнок$\PageIndex{13}$: Характеристика загальних квадричних поверхонь: еліпсоїд, гіперболоїд одного листа, гіперболоїд двох аркушів.

Ця цифра являє собою таблицю з двома стовпцями і трьома рядками. Три ряди представляють другі 6 квадратичних поверхонь: еліптичний конус, еліптичний параболоїд і гіперболічний параболоїд. Рівняння і сліди знаходяться в першій колонці. Другий стовпець містить графіки поверхонь. Еліптичний конус має два конуса, що торкаються в точках. Еліптичний параболоїд схожий на конус, але довгастий. Гіперболічний параболоїд має вигин посередині, схожий на сідло. — Малюнок$\PageIndex{14}$: Характеристики загальних квадричних поверхонь: еліптичний конус, еліптичний параболоїд, гіперболічний параболоїд.

Приклад$ \PageIndex{5}$: Identifying Equations of Quadric Surfaces

Визначте поверхні, представлені заданими рівняннями.

$ 16x^2+9y^2+16z^2=144$
$ 9x^2−18x+4y^2+16y−36z+25=0$

Рішення

а$ z$ Терміни$ x,y,$ і всі квадратні, і всі позитивні, так що це, ймовірно, еліпсоїд. Однак давайте поставимо рівняння в стандартну форму для еліпсоїда, щоб бути впевненим. У нас є

\[ 16x^2+9y^2+16z^2=144. \nonumber \]

Поділ через 144 дає

\[ \dfrac{x^2}{9}+\dfrac{y^2}{16}+\dfrac{z^2}{9}=1. \nonumber \]

Отже, це, по суті, еліпсоїд, зосереджений на початку.

б. спочатку помічаємо, що$ z$ термін піднімається тільки до першої влади, так що це або еліптичний параболоїд, або гіперболічний параболоїд. Ми також зауважимо, що існують$ x$$ y$ терміни та терміни, які не квадратні, тому ця квадратна поверхня не зосереджена на початку. Нам потрібно заповнити квадрат, щоб поставити це рівняння в одну зі стандартних форм. У нас є

\[ \begin{align*} 9x^2−18x+4y^2+16y−36z+25 =0 \\[4pt] 9x^2−18x+4y^2+16y+25 =36z \\[4pt] 9(x^2−2x)+4(y^2+4y)+25 =36z \\[4pt] 9(x^2−2x+1−1)+4(y^2+4y+4−4)+25 =36z \\[4pt] 9(x−1)^2−9+4(y+2)^2−16+25 =36z \\[4pt] 9(x−1)^2+4(y+2)^2 =36z \\[4pt] \dfrac{(x−1)^2}{4}+\dfrac{(y−2)^2}{9} =z. \end{align*}\]

Це еліптичний параболоїд з центром$ (1,2,0).$

Вправа$ \PageIndex{3}$

Визначте поверхню, представлену рівнянням$ 9x^2+y^2−z^2+2z−10=0.$

Підказка: Подивіться на ознаки і повноваження$ x,y$, і$ z$ терміни
Відповідь: Гіперболоїд одного листа, по центру в$ (0,0,1)$.

Ключові поняття

Набір ліній, паралельних даній лінії, що проходять через задану криву, називається циліндром, або циліндричної поверхнею. Паралельні лінії називаються постановами.
Перетин тривимірної поверхні і площини називається слідом. Знайти слід в $xy$-, -, або$yz$ $xz$- площинами, встановлених$ z=0,x=0,$ або$ y=0,$ відповідно.
Квадричні поверхні - це тривимірні поверхні зі слідами, що складаються з конічних перерізів. Кожна квадратна поверхня може бути виражена рівнянням форми

\[Ax^2+By^2+Cz^2+Dxy+Exz+Fyz+Gx+Hy+Jz+K=0. \nonumber \]

Щоб намалювати графік квадратної поверхні, почніть з ескізу слідів, щоб зрозуміти рамки поверхні.
Важливі чотирикутні поверхні зведені на рисунках$\PageIndex{13}$ і$\PageIndex{14}$.

Глосарій

циліндр: набір ліній, паралельних заданій лінії, що проходять через задану криву

еліпсоїд: тривимірна поверхня, описана рівнянням форми$ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}=1$; всі сліди цієї поверхні є еліпсами

еліптичний конус: тривимірна поверхня описується рівнянням форми$ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=0$; сліди цієї поверхні включають еліпси і пересічні лінії

еліптичний параболоїд: тривимірна поверхня, описана рівнянням форми$ z=\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}$; сліди цієї поверхні включають еліпси і параболи

гіперболоїд одного листа: тривимірна поверхня, описана рівнянням форми,$ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1;$ сліди цієї поверхні включають еліпси і гіперболи

гіперболоїд двох аркушів: тривимірна поверхня, описана рівнянням форми$ \dfrac{z^2}{c^2}−\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1$; сліди цієї поверхні включають еліпси і гіперболи

чотирикутні поверхні: поверхні в трьох вимірах, що мають властивість, що сліди поверхні є конічними перерізами (еліпси, гіперболи, параболи)

постанови: паралельні лінії, що складають циліндричну поверхню

слід: перетин тривимірної поверхні з координатною площиною

Визначення: циліндри та постанови

Приклад\( \PageIndex{1}\): Graphing Cylindrical Surfaces

Вправа\( \PageIndex{1}\):

Визначення: сліди

Визначення: Квадричні поверхні та конічні перерізи

Приклад\( \PageIndex{2}\): Sketching an Ellipsoid

Приклад\( \PageIndex{3}\): Identifying Traces of Quadric Surfaces

Вправа\( \PageIndex{2}\):

Приклад\( \PageIndex{4}\): Chapter Opener: Finding the Focus of a Parabolic Reflector

Приклад\( \PageIndex{5}\): Identifying Equations of Quadric Surfaces

Вправа\( \PageIndex{3}\)