10.6: Тензор напруження-енергії електромагнітного поля

Цілі навчання

• Поясніть тензор напруження-енергії для електромагнітного поля

Електромагнітне поле має пов'язаний з ним тензор напружено-енергії. З нашого дослідження електромагнетизму ми знаємо, що електромагнітне поле має щільність енергії\(U=(E^2+B^2)/8\pi k\) та щільність імпульсу\(\vec{S}=(\vec{E}\times\vec{B})/4\pi k\) (в одиницях\(c=1\), де, з\(k\) постійною Кулона). Це фіксує компоненти тензора напруження-енергії форми\(T^{t\ldots}\) і\(T^{\ldots t}\), тобто верхнього ряду і лівого стовпчика, щоб виглядати так:

\[T^{\mu\nu} = \begin{pmatrix} U & S_x & S_y & S_z \\ S_x & & & \\ S_y & & & \\ S_z & & & \end{pmatrix}\]

Малюнок\(\PageIndex{1}\): Тиск і напруга в електростатичних полах.

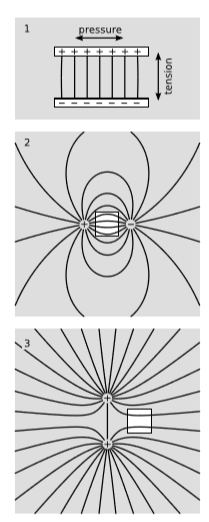
Наступний аргумент говорить нам щось про те, чого очікувати від компонентів\(T^{xx}\), і\(T^{yy}\)\(T^{zz}\), які інтерпретуються як тиск або напруженість, залежно від їх ознак. На малюнку\(\PageIndex{1}\) (1) пластини конденсатора хочуть зруйнуватися один проти одного у вертикальному (\(y\)) напрямку, але в той же час внутрішні відбиття всередині кожної пластини змушують цю пластину розширюватися в\(x\) напрямку. Якщо конденсатор побудований з матеріалів, які тримають свою форму, то електромагнітне напруження в\(T^{yy}<0\) протидіє тиску\(T^{yy}>0\) в матеріалах, тоді як електромагнітний тиск\(T^{xx}>0\) скасовується натягом матеріалів\(T^{xx}<0\). Ми отримали ці результати для конкретної фізичної ситуації, але відносність вимагає, щоб енергія стресу була визначена в кожній точці на основі полів у цій точці, тому наші висновки повинні триматися загалом. На малюнку\(\PageIndex{1}\) (2) та малюнку\(\PageIndex{1}\) (3) білі коробки були намальовані в регіонах, де загальне поле сильне, а поля сильно взаємодіють. На малюнку\(\PageIndex{1}\) (2) існує напруга у\(x\) напрямку та тиску\(y\); напруга можна розглядати як сприяння тяжіння між протилежними зарядами. У 3 також є\(x\) напруга і\(y\) тиск; тиск сприяє відштовхуванню подібних зарядів.

Щоб зробити це більш кількісним, розглянемо розрив у\(E_y\) верхній пластині на малюнку\(\PageIndex{1}\) (1). Поле різко перемикається з зовнішньої сторони\(0\) на деяке значення\(E\) між пластинами. За законом Гаусса, заряд на одиницю площі на плиті повинен бути\(\sigma=E/4\pi k\). Середнє поле, яке відчуває заряд в пластині\(\overline{E}=(0+E)/2=E/2\), є, тому сила на одиницю площі, тобто напруга в полі, є\(\sigma \overline{E}=E^2/8\pi k\). Таким чином, ми очікуємо\(E\),\(T^{yy}=-E^2/8\pi k\) якщо знаходиться вздовж\(y\) осі.

Для читача, який хоче повного виведення решти дев'яти компонентів тензора, тепер ми наведемо аргумент, який використовує наступний список його властивостей. Інші читачі можуть пропустити вперед туди, де представлений повний тензор.

1. \(T\)симетрична,\(T^{µν} = T^{νµ}\).
2. Компоненти повинні бути другого порядку в полах, наприклад, ми можемо мати такі терміни\(E_xB_z\), як, але ні\(E_{x}^{3} B_{z}^{7}\) або\(E_xB_zB_y\). Це пояснюється тим, що рівняння Максвелла лінійні, і коли хвильове рівняння ідеально лінійне, відповідне енергетичне вираження є другим порядком за амплітудою хвилі.
3. \(T\)має властивості парності, описані в прикладі 9.2.3.
4. Електричне та магнітне поля обробляються симетрично в рівняннях Максвелла, тому їх слід розглядати симетрично в тензорі напруження-енергія. Наприклад, ми могли б мати термін\(7E_{x}^{2} + 7B_{z}^{2}\), як, але ні\(7E_{x}^{2} + 6B_{z}^{2}\).
5. У розділі 9.2 ми побачили, що стан енергії слідів\(T^a\: _a \geq 0\) задовольняється хмарою пилу тоді і тільки тоді, коли масова енергія пилу не транспортується зі швидкістю, більшою ніж\(c\). У розділі 4.1 ми побачили, що всі ультрарелятивістські частинки мають однакові механічні властивості. Оскільки хмара пилу, в межі, куди наближається його швидкість\(c\), знаходиться на краю обмеженого, встановленого умовою енергії сліду, ми очікуємо\(T^a\: _a \rightarrow 0\), що електромагнітне поле, в якому збурень поширюються на\(c\), також має точно насичувати стан сліду енергії, так що \(T^a\: _a = 0\).
6. Тензор стрес-енергії повинен вести себе належним чином при обертаннях, що в основному означає\(x\)\(y\), що, і\(z\) слід ставитися симетрично.
7. Електромагнітна плоска хвиля, що поширюється в\(x\) напрямку, не повинна чинити ніякого тиску в\(y\) або\(z\) напрямках.
8. Якщо поле підпорядковується рівнянням Максвелла, то умова енергозбереження\(\frac{\partial T^{ab}}{\partial x^a} = 0\) повинна триматися.

Цих фактів цілком достатньо, щоб повністю визначити форму решти дев'яти складових тензора стрес-енергії. Властивість 3 вимагає, щоб всі ці компоненти були навіть під паритетністю. Оскільки електричні поля перевертаються під паритетністю, але магнітні поля не мають (приклад 10.3.1), ці компоненти можуть мати лише такі терміни, як\(E_i E_j\) і\(B_i B_j\), а не змішані терміни, як\(E_i B_j\). Беручи до уваги властивості 4 і 6, ми знаходимо, що діагональні члени повинні виглядати так

і позадіагональні

Власність 5 дає\(1/2-a-3b=0\) і 7 дає\(b=-a/2\), так що у нас\(a=-1\) і\(b=1/2\). Визначення\(c=-1\) залишають як вправу, завдання Q4.

Зараз ми встановили повний вираз для тензора напруження-енергії електромагнітного поля, який

де

і\(\sigma\), відомий як тензор напруги Максвелла, задається

Все це може бути виражено більш компактно і координатно-незалежним способом, як

\[T^{ab} = \frac{1}{4\pi k} \left(\mathcal{F}^{ac}\mathcal{F}^b\: _c + \frac{1}{4}o^do_dg^{ab}\mathcal{F}_{ef}\mathcal{F}^{ef}\right)\]

де\(\vec{o}\) - вектор швидкості, спрямований на майбутнє, так що\(o^do_d=+1\) для підпису\(+---\) використовується в цій книзі, і\(-1\) якщо підпис є\(-+++\).

Приклад\(\PageIndex{1}\): Stress-energy tensor of a plane wave

Нехай електромагнітна плоска хвиля (не обов'язково синусоїдальна) поширюється уздовж\(x\) -осі, з її поляризацією такою, що\(\vec{E}\) знаходиться в\(y\) напрямку і\(\vec{B}\) на\(z\) осі, і\(|\vec{E}| = |\vec{B}| = A\). Тоді ми маємо наступне для тензора енергії стресу.

\[T^{\mu \nu } = \frac{A^2}{4\pi k} \begin{pmatrix} 1 & 1 & 0 & 0\\ 1 & 1 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \end{pmatrix}\]

\(T^{tt}\)Компонент говорить нам про те, що хвиля має певну щільність енергії. Оскільки хвиля безмасова, ми маємо\(E^2 - p^2 = m^2 = 0\), тому щільність імпульсу така ж, як і щільність енергії, і\(T^{tx}\) така ж, як\(T^{tt}\). Якщо ця хвиля вдарить по поверхні в\(yz\) площині, імпульс, який поверхня поглинає від хвилі, буде відчуватися як тиск, представлений\(T^{xx}\).

У ультрарелятивістської межі\(v →1\) це стає

\[T^{\mu \nu } = \text{(energy density)} \times \begin{pmatrix} 1 & 1 & 0 & 0\\ 1 & 1 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \end{pmatrix}\]

який точно такий же, як результат для нашої електромагнітної хвилі. Це ілюструє факт, розглянутий у розділі 4.1, що всі ультрарелятивістські частинки мають однакові механічні властивості.

Приклад\(\PageIndex{2}\): Mass of a capacitor

Малюнок\(\PageIndex{2}\): Маса конденсатора.

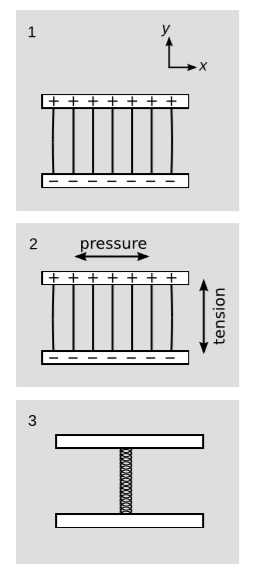
Розглянемо масу зарядженого паралельно пластинчатого конденсатора, малюнок\(\PageIndex{2}\) (1), спочатку в його рамці спокою, а потім в кадрі, посиленому в напрямку, паралельному полю (перпендикулярно пластинам). Якщо ми не будемо обережні, ми зіткнемося з наступним парадокс. Під наддувом електричне поле, паралельне наддуву, залишається незмінним. Тому в посиленому кадрі ми маємо точно таку ж напруженість поля, але заповнюючи об'єм, який був зменшений за рахунок скорочення довжини. Тому масова енергія конденсатора найбільша у власному кадрі спокою, що абсурдно і суперечить нашому доказу в розділі 9.3, що енергія-імпульс ізольованої системи перетворюється як чотири-вектор.

Там рішення парадоксу походить від визнання того, що ми припускали, що конденсатор знаходиться в статичній рівновазі, але ми ігнорували напруження-енергію будь-яких механічних опор підтримували цю рівновагу. Якщо розглядати тільки напруження-енергію\(T_{(em)}\) електромагнітного поля, то маємо\(T_{(em)}^{tt} = \frac{1}{8\pi k}E^2\) (щільність енергії) і\(T_{(em)}^{yy} = -\frac{1}{8\pi k}E^2\) (напруга в\(y\) напрямку, паралельно полю), малюнок\(\PageIndex{2}\) (2). Легко помітити, що це має незникаючу розбіжність, так як\(\partial _y T_{(em)}^{yy} \neq 0\) у пластин і немає інших термінів в тензорі стрес-енергії, які могли б це компенсувати.

Тут немає нічого дивного; тільки тензор загальної енергії стресу\(T\) повинен бути безмежним, ні\(T_{(em)}\). Це порушило б закони фізики, якби конденсатор залишався в рівновазі, як це, без певної сили для протидії електромагнітному напруженню. Припустимо, що це зусилля забезпечується пружиною, як на малюнку\(\PageIndex{2}\) (3). Весна має свій\(T_{(s)}\) внесок у стрес-енергію. Для зручності уявімо, як зробити пружину заповненою (а не порожнистим циліндром) і відгодувати її так, щоб вона заповнила весь внутрішній обсяг конденсатора. Тоді для досягнення статичної рівноваги в рамі відпочинку нам потрібен тиск у пружині, щоб скасувати тиск в електричному полі. Тому ми маємо\(T^{yy} = 0\) для загального тензора енергії стресу.

Якщо ми зараз застосуємо закон тензорного перетворення до тензора енергії стресу, то виявимо, що тензор енергії напруження-енергії в посиленому кадрі містить щільність масової енергії\(T^{t't'}\), яка залежить тільки від\(T^{tt}\) і\(T^{yy}\). (Там також повинен бути\(xx\) компонент, щоб пластини не вибухали збоку, але це не входить сюди.) Але ми маємо\(T^{yy} = 0\), тому проблема точно така ж, як перетворення грудки нерелятивістської матерії, і ми знаємо, що цей розрахунок виходить добре. Для явної демонстрації того, що це все ще працює, якщо відкинути спрощене припущення, що пружина заповнює весь внутрішній об'єм конденсатора, див. Ріндлер і Денур, «Простий релятивістський парадокс про електростатичну енергію» Am J Phys 56 (1988) 9.