10.7: Рівняння Максвелла

Цілі навчання

• Поясніть рівняння Максвелла

Заява і тлумачення

У цій книзі я припускаю, що у вас був звичайний фізичний фон, придбаний в курсі опитування першокурсника, який включає в себе початкову, ймовірно, страхітливу, зустріч з рівняннями Максвелла в інтегральній формі. У одиницях з$c=1$ рівняннями Максвелла є:

Рівняння Максвелла

$$\Phi_E = 4\pi kq$$

$$\Phi_B = 0$$

$$\oint \vec{E}\cdot dl = -\frac{\partial \Phi _B}{\partial t}$$

$$\oint \vec{B}\cdot dl = \frac{\partial \Phi _E}{\partial t} + 4\pi kI$$

де

$$\Phi_E = \int E\cdot da$$

і

$$\Phi_B = \int B\cdot da$$

Рівняння$\PageIndex{1}$ і$\PageIndex{2}$ відносяться до замкнутої поверхні і заряду, що$q$ міститься всередині цієї поверхні. Рівняння, закон Гаусса, говорить, що заряди є джерелами електричного поля, в той час як говорить, що магнітних «зарядів» не існує. Рівняння$\PageIndex{3}$ і$\PageIndex{4}$ посилаються на поверхню, як картопляний чіп, який має ребро або межу, і струм, що$I$ проходить через цю поверхню, з лінійними інтегралами, які оцінюються вздовж цієї межі. Права сторона говорить про те, що мінливе магнітне поле виробляє фігурне електричне поле, як в генераторі або трансформаторі. $I$Термін в говорить про те, що струми створюють магнітні поля, які згортаються навколо них. $\partial \Phi_E/\partial t$Термін, який говорить про те, що змінюються електричні поля створюють магнітні поля, необхідний для того, щоб рівняння давали послідовні результати незалежно від обраних поверхонь, а також є частиною апарату, що відповідає за існування електромагнітних хвиль, в яких змінюється$\vec{E}$ поле виробляє$\vec{B}$, а зміна$\vec{B}$ робить$\vec{E}$.

Рівняння$\PageIndex{1}$ і не$\PageIndex{2}$ мають залежності від часу. Вони функціонують як обмеження на можливі шаблони полів. Рівняння$\PageIndex{3}$ і$\PageIndex{4}$ є динамічними законами, які передбачають, як початкова картина поля буде розвиватися з часом. Можна показати, що якщо$\PageIndex{1}$ і$\PageIndex{2}$ задовольняються спочатку, то$\PageIndex{3}$ і$\PageIndex{4}$ гарантують, що вони і надалі будуть задоволені пізніше. Оскільки динамічні закони складаються з двох векторних рівнянь, вони забезпечують загальну кількість$6$ обмежень, які є числом, необхідним для прогнозування поведінки$6$ полів$E_x$$E_y$,$E_z$,$B_x$,$B_y$, і$B_z$. <% end_sec ('maxwell-оператор')

Експериментальна підтримка

До роботи Ейнштейна 1905 року про відносність відомими законами фізики були законами Ньютона і рівняннями Максвелла. Експерименти, такі як приклад 4.2.3 показують, що закони Ньютона - це лише низькошвидкісні наближення. Рівняння Максвелла - це низькошвидкісні наближення; наприклад, в розділі ми відзначили докази того, що атоми електрично нейтральні, відповідно до закону Гаусса$\PageIndex{1}$, Рівняння$10^{21}$, до однієї частини в, хоча електрони в атомах зазвичай мають швидкості на порядку$1-10\%$ $c$.

Несумісність з галілеєвим простором-часом

Рівняння Максвелла не сумісні з галілейським описом простору-часу (розділ 1.1). Якщо ми припустимо, що рівняння тримаються в деякому кадрі$\vec{o}$, а потім застосуємо галілеєве прискорення$(t',x',y',z')=(t,x-vt,y,z)$, перетворюючи координати$(t,x,y,z)$ в, ми виявимо, що в кадрі$\vec{o}'$ рівняння мають іншу і складнішу форму, яку неможливо спростити, щоб виглядати як форма, яку вони мали в $\vec{o}$. Замість того, щоб виписувати отриманий жахливий безлад і перевіряти, що він не може бути відкинутий назад у простішу форму, простіший спосіб довести це, щоб відзначити, що існують рішення рівнянь в$\vec{o}$ які не є рішеннями після галілейського імпульсу в$\vec{o}'$, якщо ми намагаємося зберегти рівняння в тієї ж форми. Наприклад, якщо світлова хвиля поширюється в$x$ напрямку зі швидкістю$c$ в$\vec{o}$, то після імпульсу, у нас буде легка хвиля в кадрі$v=c$,$\vec{o}'$ який стояв на місці. (Це мислимий експеримент Ейнштейна з їзди поряд з легкою хвилею на мотоциклі, розділ 1.1.) Така хвиля порушила б рівняння$\PageIndex{3}$, оскільки ліва сторона була б ненульовою для поверхні, що лежить на$xy$ площині, але похідна часу на правій стороні дорівнювала б нулю.

Чи не явно релятивістські в первозданному вигляді

Оскільки рівняння Максвелла не є низькошвидкісними наближеннями і несумісні з галілейською відносністю, ми очікуємо з користю історичного заднього огляду, що вони сумісні з релятивістською картиною простору-часу. Але коли вони виражені в наведеній вище формі, у них є дві особливості, або одна з яких здається достатньою, щоб зробити їх повністю несумісними з відносністю:

1. Вони, як видається, описують миттєву дію на відстані. Наприклад, закон Гаусса$Φ_E = 4πkq$, пов'язує електричне поле в одному місці (на замкнутій поверхні) з електричним зарядом десь ще (всередині поверхні). Ця нелокальна структура пахне неправильно релятивістично, з причин, розглянутих у розділі 10.2.
2. Вони, здається, ставляться до часу і простору асиметрично.

Що насправді відбувається тут, так це те, що рівняння Максвелла схожі на версію, написану олівцем на довгій смужці туалетного паперу. Вони повністю релятивістські, але були написані у формі, яка приховує цей факт.

Проблема нелокальності може бути показана як непроблема$i$, оскільки рівняння Максвелла можуть бути перероблені у форму, в якій вони є чисто локальними. Ідея показана на малюнку$\PageIndex{1}$.

Малюнок$\PageIndex{1}$: Магнітне поле, яке порушує$Φ_B = 0$.

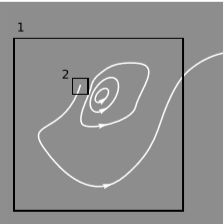
Лінії магнітного поля утворюють замкнуті петлі, за винятком однієї з них, яка починається в точці простору і поширюється до нескінченності. Малюючи велику коробку, 1, ми виявляємо$\Phi_{B,1}$, що потік магнітного поля через коробку не дорівнює нулю, тому що лінія залишає коробку, але жодна не входить. Але така ж розбіжність могла бути виявлена з меншою коробкою 2, або насправді з довільно маленьким ящиком, що містить джерело рядка поля. Іншими словами, рівняння$\Phi_B=0$ є нелокальним, але якщо його потрібно утримувати для будь-якої поверхні, то воно також повинно триматися локально, в межі довільно малої поверхні. Цей чисто закон фізики можна виразити за допомогою тривимірного варіанту розбіжності, введеного в розділі 9.1:

З чотирьох рівнянь Максвелла обидва рівняння$\PageIndex{1}$ і$\PageIndex{2}$ можуть бути перевиражені таким чином. Ця книга не представляє повного механізму векторного обчислення і не передбачає попередніх знань про нього, але аналогічна гранична процедура також може бути застосована до рівнянь$\PageIndex{3}$ і$\PageIndex{4}$, використовуючи оператор, який називається завиток.

Наступний приклад - це той, в якому і проблема, і проблема виявляються не проблемами.

Приклад$\PageIndex{1}$: Jumping through a hoop

Малюнок$\PageIndex{2}$: 1. Електрон стрибає через обруч. Альтернативна поверхня, що охоплює обруч.

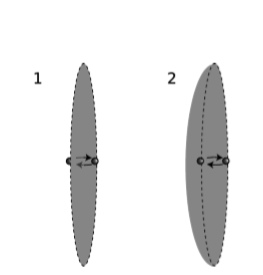
Ось приклад, в якому неочевидні особливості рівнянь Максвелла перешкоджають антирелятивістському кривленню, проектованому на i. на малюнку$\PageIndex{2}$ (1) електрон стрибає туди-сюди через уявний круговий обруч, через який ми будуємо уявну плоску поверхню. Кожен раз, коли електрон пробиває поверхню, він робить миттєвий сплеск струму$I$, який з'являється в:

$$\oint \vec{B}\cdot dl = \frac{\partial \Phi _E}{\partial t} + 4\pi kI$$

Ми можемо очікувати, що це призведе до того, що поле,$B$ виявлене на краю диска, одночасно показуватиме подібні шипи. Але «ті ж часи» передбачає деяке поняття одночасності, і це було б несумісно з відносністю, оскільки t координата, про яку згадується тут, є лише поняттям часу одного спостерігача. Крім того, здавалося б, інформація передавалася миттєво від центру диска до його краю, що порушує відносність.

Тим не менш, ми можемо створити очевидний парадокс, навіть не звертаючись до відносності. Замість плоскої поверхні на малюнку$\PageIndex{2}$ (1) ми можемо вибрати форму посуду, фігуру$\PageIndex{2}$ (2), з досить глибокою кривою, щоб електрон ніколи не перетинав її. Струм I завжди дорівнює нулю відповідно до цієї поверхні, так що жодне поле не$B$ буде вироблятися на ободі взагалі.

Вирішення всіх цих труднощів полягає в терміні$∂Φ_E/∂t$, який ми проігнорували. З поверхнею 1 електрон перетинає поверхню у часі$δt$, викликаючи струм,$I = e/δt$ але також викликаючи зміну потоку від$Φ_E ≈ 2πke$ до$Φ_E ≈ -2πke$. Результатом є те, що права частина рівняння майже дорівнює нулю. З поверхнею 2,$I = 0$ і$∂Φ_E/∂t ≈ 0$, таким чином, права сторона знову майже нуль.

Коли наближення, використані вище, усуваються, рівняння Максвелла передбачають незникаюче поле, яке є очікуваною електромагнітною хвилею, що поширюється від електрона з належною швидкістю$c$.

інваріантність Лоренца

Приклад$\PageIndex{1}$ може здатися «просто так історією», але, мабуть, чудодійна резолюція - це не випадковість. Це відбувається тому, що рівняння Максвелла насправді інваріантні під трансформацією Лоренца, хоча це не очевидно, коли вони написані у формі, наведеній вище. Існують різні способи показати це:

• Ейнштейн зробив це грубою силою у своїй статті 1905 року про відносність, перетворюючи координати через перетворення Лоренца та поля, як у розділі 10.4.
• Рівняння Максвелла - це в основному хвильові рівняння. (Вони мають як хвильові рішення, так і статичні рішення.) Ми можемо перевірити, що коли ми починаємо з синусоїдальної плоскої хвилі в одному кадрі, а потім перетворюємося в інший кадр, результат знову є дійсним синусоїдальним рішенням, піддавшись доплерівському зсуву (розділ 3.2) та аберації (розділ 6.5). Це вимагає перевірки того, що хвиля все ще чисто поперечна, але це легко випливає з вивчення інваріантів, описаних у розділі 10.5. За відомим математичним результатом, званим теоремою Фур'є, будь-яка добре поведена хвиля може бути записана як сума синусоїдальних хвиль, і тому будь-яке хвильове рішення рівнянь Максвелла в одному кадрі також є рішенням у кожному іншому кадрі.
• Рівняння Максвелла можна переписати з точки зору тензорів, підкоряючись всім граматичним правилам індексної гімнастики. Якщо їх можна записати в такому вигляді, вони автоматично стають інваріантними Лоренца.

Останній підхід є найбільш загальним і елегантним, тому ми наведемо короткий ескіз того, як він працює. Рівняння$\PageIndex{1}$ має$4\pi$ рази заряд праворуч, в той час як має$4\pi$ рази струм. Вони обидва відносяться до поточних чотиривекторних$\vec{J}$, тому чітко нам потрібно об'єднати їх якось в єдине рівняння з$\vec{J}$ праворуч. Оскільки локальна форма рівняння передбачає тривимірну розбіжність, яка містить перші похідні, ліва сторона цього комбінованого рівняння повинна мати в ньому першу похідну. Враховуючи граматичні правила тензорів та індексної гімнастики, у нас не так багато можливих способів досягти цього. Єдине очевидне, що потрібно спробувати, це

$$\frac{\partial \mathcal{F}^{\mu\nu}}{\partial x^\nu} = 4\pi k J^\mu$$

$\mu$Виписуючи це за часову координату, ми отримуємо відношення, яке прирівнює розбіжність$\vec{E}$ до$4\pi$ разів щільності заряду; це локальний еквівалент Рівняння$\PageIndex{1}$. Якщо ви взяли векторне обчислення і знаєте про оператор curl і теорему Стокса, то ви можете перевірити, що$\mu$ для посилання$x$, і$y$$z$, ми відновлюємо локальну форму Рівняння$\PageIndex{4}$. Тензорний спосіб вираження рівняння$\PageIndex{2}$ та рівняння$\PageIndex{3}$ виявляється

$$\frac{\partial \mathcal{F} ^{\mu\nu}}{\partial x^\lambda} + \frac{\partial \mathcal{F} ^{\nu\lambda}}{\partial x^\mu} + \frac{\partial \mathcal{F} ^{\lambda\mu}}{\partial x^\nu} = 0$$

Приклад$\PageIndex{2}$: A generator

Малюнок$\PageIndex{3}$: Сирий, непрактичний генератор.

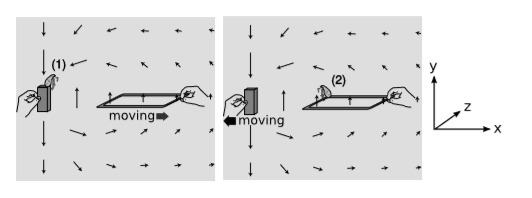
$\PageIndex{3}$На малюнку зображений грубий, непрактичний генератор, зображений в двох системах відліку.

Блоха 1 сидить на вершині стрижневого магніту, який створює малюнок магнітного поля, показаний стрілками. Для неї стрижневий магніт, очевидно, знаходиться в стані спокою, і ця картина магнітного поля статична. Коли квадратна петля дроту відтягується від неї та магніту, її протони відчувають силу в$z$ напрямку −, як визначено законом сили Лоренца$\vec{F} = q\vec{v} × \vec{B}$. Електрони, які негативно заряджені, відчувають силу в$+z$ напрямку. Електрони провідності вільні рухатися, але протони - ні, на передній і задній сторонам петлі ця сила перпендикулярна дроту. Однак у правій і лівій стороні електрони вільні реагувати на силу. Так як магнітне поле слабше з правого боку, струм циркулює навколо петлі.

Блоха 2 сидить на петлі, яку вона вважає перебувати в стані спокою. У її рамці відліку це стрижневий магніт, який рухається. Як і flea 1, вона спостерігає струм, що циркулює навколо петлі, але на відміну від flea 1, вона не може використовувати магнітні сили для пояснення цього струму. Що стосується неї, то електрони спочатку знаходилися в стані спокою. Магнітні сили - це сили між рухомими зарядами та іншими рухомими зарядами, тому магнітне поле ніколи не може прискорити заряджену частинку, починаючи з відпочинку. Силою, яка прискорює заряд від спокою, може бути тільки електрична сила, тому вона змушена зробити висновок, що в її області простору є електричне поле. Це поле рухає електрони навколо і навколо по колу — це фігурне поле. Яку причину може запропонувати flea 2 для існування цієї схеми електричного поля? Ну, вона помітила, що магнітне поле в її області простору змінюється, можливо, тому, що цей стрижневий магніт там стає все далі. Вона зауважує, що мінливе магнітне поле створює фігурне електричне поле. Таким чином,$∂Φ_B/∂t$ термін у рівнянні ($\PageIndex{3}$) не є необов'язковим; він повинен існувати, якщо рівняння Максвелла мають бути однаково дійсними у всіх кадрах.

Ейнштейн відкриває свою роботу 1905 року про відносність ¹ починається з цього речення: «Відомо, що електродинаміка Максвелла - як зазвичай розуміється в даний час - при застосуванні до рухомих тіл призводить до асиметрій, які, здається, не притаманні явищам». Потім він наводить по суті цей приклад. Хоча спостерігачі в кадрах 1 і 2 погоджуються з усіма фізичними вимірами, їх пояснення фізичних механізмів, викладених мовою рівнянь Максвелла в формі, абсолютно різні. У релятивістській мові пояснення flea 2 можна записати через рівняння$\PageIndex{9}$, у випадку, коли індекси є$x$$z$, і$t$:

$$\frac{\partial \mathcal{F} ^{xz}}{\partial t} + \frac{\partial \mathcal{F} ^{zt}}{\partial x} + \frac{\partial \mathcal{F} ^{tx}}{\partial z} = 0$$

який такий же, як

$$\frac{\partial B_y}{\partial t} + \frac{\partial E_z}{\partial x} + \frac{\partial E_x}{\partial z} = 0$$

Оскільки перший термін негативний, другий термін повинен бути позитивним. Оскільки рівняння$\PageIndex{8}$ і пишуться в$\PageIndex{9}$ терміні тензорів, підкоряючись граматичним правилам індексної гімнастики, ми гарантуємо, що вони дають послідовні прогнози у всіх рамках відліку.

Приклад$\PageIndex{3}$: Conservation of charge and energy-momentum

Розв'язуючи рівняння$\PageIndex{8}$ для вектора струму, ми маємо

$$J^\mu = \frac{1}{4\pi k }\frac{\partial \mathcal{F}^{\mu\nu}}{\partial x^\nu}$$

Збереження заряду (розділ 9.1) може виражатися як

$$\frac{\partial J^\mu }{\partial x^\mu} = 0$$

Якщо підставити перше рівняння в друге, отримаємо

$$\frac{\partial }{\partial x^\mu} \left ( \frac{1}{4\pi k }\frac{\partial \mathcal{F}^{\mu\nu}}{\partial x^\nu} \right ) = 0$$

або

$$\frac{\partial^2 \mathcal{F}^{\mu\nu}}{\partial x^\mu \partial x^\nu} = 0$$

з сумою над обома$µ$ і$ν$. Але це рівняння автоматично$\mathcal{F}$ задовольняється, оскільки є антисиметричним, тому для кожної комбінації індексів$µ$ і$ν$, термін залучення$\mathcal{F}^{µν}$ скасовується одним, що містить$\mathcal{F}^{νµ} = -\mathcal{F}^{µν}$. Таким чином, збереження заряду не потрібно додавати як додаткову умову на додаток до рівнянь Максвелла; це автоматично мається на увазі рівняннями Максвелла.

Посилання

¹ «Зур Електродинамік бегтер К рупер», Аннален дер Фізик. 17 (1905) 1981 р. Переклад Перретта та Джеффрі

Дописувач

• Template:ContribSRCrowell