10.4: Трансформація полів

Last updated
Save as PDF

Page ID: 77381

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Поясніть наступні закони в рамках Закону про ідеальний газ

Оскільки ми пов'язували компоненти електричного та магнітного полів з елементами тензора рангу 2, закон трансформації для цих полів тепер випливає із загального закону тензорного перетворення для\(2\) ранг-тензорів (розділ 9.2). Ми спочатку викладемо загальне правило, в привіреному вигляді, а потім наведемо кілька конкретних прикладів. Під імпульсом з трьома\(\vec{v}\) швидкостями електричні та магнітні поля\(\vec{E}\)\(\vec{B}\) трансформуються\(\vec{E}'\) і\(\vec{B}'\) відповідно до цих правил:

Приклад\(\PageIndex{1}\): A line of charge

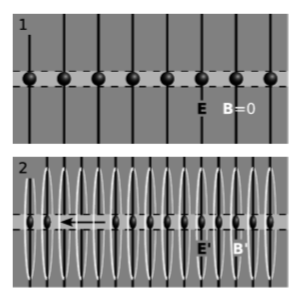
рис. 10.4.1.png — Малюнок\(\PageIndex{1}\): Лінія заряду.

На малюнку\(\PageIndex{1}\) (1) показана лінія зарядів. У даній сусідній точці він створює електричне поле,\(E\) яке вказує назовні, як вимірюється спостерігачем,\(o\) який знаходиться в спокої щодо зарядів. Це поле представлено на малюнку своїм малюнком польових ліній, які починаються на зарядах і випромінюють назовні, як щетина пляшкової кисті. Оскільки заряди знаходяться в стані спокою, магнітне поле дорівнює нулю. (Знаходження величини поля на певній відстані - це пряме застосування закону Гаусса.)

Тепер розглянемо спостерігача\(o'\), малюнок\(\PageIndex{1}\) (2), що рухається\(v\) зі швидкістю вправо щодо\(o\). Навіть не турбуючись про те, як було створено поле, ми можемо перетворити поля, в тій точці простору, яка обговорювалася раніше, в новий кадр. Результат -\(E' = γE\) і\(B'_⊥ = -γv × E\). У цьому кадрі електричне поле більш інтенсивне, а також є магнітне поле, малюнок якого з ліній білого поля утворює кола, що лежать в площинях, перпендикулярних лінії. Якщо нам трапляється знати, що поле було створено лінією заряду, яка рухається відповідно до\(o'\), то ми можемо пояснити ці результати як випливають з двох ефектів. По-перше, лінія заряду була подовжена. Це призводить до збільшення щільності заряду на одиницю довжини в рази\(γ\), при пропорційному збільшенні електричного поля. У описі рядка поля ми просто маємо більше зарядів на малюнку, тому з них виходить більше ліній полів. По-друге, лінія заряду рухається вліво в цьому кадрі, тому вона утворює електричний струм, і цей струм є причиною виникнення магнітного поля\(B'\).

Приклад\(\PageIndex{2}\): A moving charge

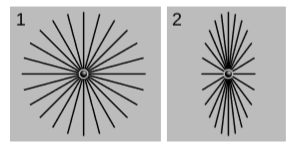
рис. 10.4.2.png — Малюнок\(\PageIndex{2}\): Рухомий заряд.

На малюнку\(\PageIndex{2}\) (1) показані лінії електричного поля заряду, в кадрі спокою заряду\(K\). На малюнку\(\PageIndex{2}\) (2) ми бачимо таке ж електричне поле, в кадрі,\(K'\) в якому заряд рухається уздовж\(x\) -осі, яка вказує вправо, в\(90\%\) of\(c\). (У цьому кадрі також є магнітне поле, яке не показано.) Це електричне поле, яке змінюється в часі, показано у вигляді знімка в гіперплощині\(t' = 0\) одночасності\(K'\). Дивно, але ці лінії поля всі вказують на теперішнє положення заряду в\(K'\).

Збурення в електромагнітному полі поширюються на\(c\), а не миттєво, тому можна було очікувати, що поле\(P\) в певному місці на цьому малюнку вкаже на місце на відстані\(r\), яку заряд займав у більш ранній час\(t' = -r/c\). Це створило б набір вигнутих ліній поля, що нагадують поминки човна. Щоб побачити, що це неможливо, розглянемо точку\((0, 0, h, 0)\) в координатах Мінковського\(K\), тобто точку на\(y\) -осі. Після перетворення Лоренца уздовж\(x\) координати цієї точки в\(K'\) залишаються\((0, 0, h, 0)\), так що в\(K'\) також лежить на лінії, яка проходить поперечно через теперішнє положення заряду. Оскільки ця точка має\(E_x = 0\) і\(\vec{B} = 0\) в\(K\), застосування законів трансформації показує, що\(E'_x = 0\) також, так що поле вказує на теперішнє положення заряду, а не на його минуле положення.

Подібний, але більш складний розрахунок показує, що поле під проміжними кутами також знаходиться в миттєво радіальному напрямку. Замість того, щоб заповнювати деталі, ми зауважимо, що це має сенс, оскільки вектор Пойнтінга\(\vec{E} × \vec{B}\) тоді не має радіальної складової, що, як очікується, оскільки енергія повинна транспортуватися вперед, але не випромінюватися назовні.

Можна хвилюватися, що це вказуватиме на те, що інформація про положення заряду поширювалася миттєво, суперечивши відносності. Але це заряд, який завжди був у своєму поточному стані руху і завжди буде. Якби рух заряду був порушений деякою зовнішньою силою в той час пізніше\(t' = -r/c\), ніж, лінії поля все одно вказували\(K\) б на місце, яке раніше займав заряд, перебуваючи в стані спокою, і поле в\(K'\) буде вказувати на його лінійно екстрапольоване положення.

Приклад\(\PageIndex{3}\): A field behaving like a stick

Рисунок\(\PageIndex{2}\) (2) виглядає ідентичним копії фігури\(\PageIndex{2}\) (1), яка була укладена Лоренцем\(1/γ\), і ми можемо перевірити за законами трансформації для полів, що це правильно. Оскільки ці закони трансформації застосовуються незалежно від того, як були створені поля, ми маємо загальне правило, яке полягає в тому, що якщо поле є чисто електричним в одному кадрі, то його напрямок перетворюється на інший кадр так само, як напрямок палиці, коли ми трансформуємося з рамки спокою палиці.

Взагалі неправда, що лінії електричного поля можна просто переносити з одного кадру в інший так, ніби ми Лоренц контрактували щуре гніздо, побудоване з дроту. Це властивість має тільки тоді, коли вихідна рамка має зовсім особливий вид: каркас, в якому поле суто електричне. (Ми завжди можемо знайти такий кадр, якщо\(E^2 > B^2\); див. Розділ 10.5.) Як контрприклад до поняття про те, що воно застосовується більш загально, розглянемо випадок, в якому поле є чисто магнітним в певному кадрі. Тоді лінії електричного поля навіть не існують у вихідному кадрі, а існують в новому.

Повертаючись до випадку, коли вихідне поле є чисто електричним, так що поведінка, схожа на паличку, дійсно тримається, не відразу очевидно, чому має бути така дивна відповідність між палицями і лініями поля. Методи, що використовуються в задачі Q3 глави 2, здається, не мають багато спільного з тими, які ми використовували для визначення того, як поводиться електричне поле. Але наступний фізичний аргумент показує, що існує проста причина ідентичної поведінки.

Розглянемо палицю з зарядами\(+q\) і\(-q\) закріплені на кінцях. Паличка не обертається і рухається інерційно. У кадрі решти палиці є лінія поля\(K\), що походить від\(+q\) і закінчується на\(-q\) якій збігається з палицею. Тепер розглянемо каркас,\(K'\) що рухається в деякому напрямку щодо палиці. Як обговорювалося в прикладі 10.4.2, поле за рахунок кожного заряду вказує в бік або від його теперішнього миттєвого положення в а\(K'\) також\(K\). Тому кожне поле, у палиці, паралельно палиці, і у нас знову є лінія поля в\(K'\) тому, що збігається з палицею. Оскільки перетворення поля не залежить від того, як було створено поле, це стосується будь-якого поля, яке є чисто електричним у вихідному кадрі.