8.7: Космологічні рішення (частина 4)

Рішення, яке переважає радіація

З причин, розглянутих у прикладі 14, у ранньому Всесвіті переважало випромінювання. Розв'язок рівнянь Фрідмана для цього випадку розглядається в задачі 11.

Локальні наслідки розширення

У цьому розділі ми обговорюємо прогнози загальної відносності щодо впливу космологічного розширення на малі, гравітаційно пов'язані системи, такі як Сонячна система або скупчення галактик. Коротка відповідь полягає в тому, що в більшості реалістичних космологій (але не обов'язково в сценаріях «Big Rip») ефект розширення не нульовий, а багато порядків занадто малий для вимірювання. Багато читачів, ймовірно, будуть готові прийняти ці твердження, пропускаючи наступні демонстрації.

Для початку ми спостерігаємо, що існує два якісно чітких типу ефектів, які могли б існувати. Припустимо, що піднімається буханець хліба з родзинками. Припустимо, що коефіцієнт масштабу хліба a подвоюється до часу витрачених зусиль дріжджів. За визначенням це означає, що родзинки (галактики, тестові частинки) отримують далі один від одного в 2 рази. Ми могли б уявити, що крім того: (1) деформація розширення може призвести до того, що кожен родзинки затягнуться, скажімо, на 1%, і зберегти цей збільшений розмір протягом усього курсу розширення; або що (2) розширення може призвести до того, що кожен родзинки поступово розширюється, до 0,2% більше, ніж його початковий розмір, потім на 0,4% більше, ніж його початковий розмір і так далі, поки, в кінці процесу, кожен не виріс за свій початковий розмір на деяку суму, наприклад, 3,8%, що, хоча і менше, ніж 100% зростання міжродзинкових відстаней, все ж було ненульовим. Астрономи називають другу можливість «світським» трендом. Наприклад, моделювання сонячних систем часто показують, що протягом мільярдів років планети поступово мігрують або всередину, або назовні, під впливом своїх гравітаційних взаємодій з іншими планетами. Як приклад розширення без світської тенденції астероїди можуть відчувати незначну\(\frac{1}{r^{2}}\) силу через радіаційний тиск від сонця. Ефект точно такий, як якщо б маса сонця або гравітаційна константа були трохи зменшені. Закон еліптичної орбіти Кеплера дотримується, закон періодів трохи вимкнений, а радіус орбіти показує нульову тенденцію з часом.

Якщо існує будь-який тип ефекту, спостерігач у якомусь локальному інерційному кадрі інтерпретує його як «силу». (Лапки лякають - це нагадування про те, що загальна відносність не описує гравітацію як лінійно адитивну, миттєву дію на відстані в стилі Ньютона.) Така сила, якщо вона існує, не може бути просто пропорційною швидкості розширення\(\frac{\dot{a}}{a}\). Як контрприклад, Всесвіт Мілна - це просто плоский простор-час, описаний у дурних координатах, і він має\(\dot{a} \neq 0\).

Було б доцільніше, щоб сила залежати від другої похідної коефіцієнта масштабу. Щоб виправдати це точніше, уявіть собі, що вивільняють дві тестові частинки, спочатку розділені деякою відстанню, яка набагато менше, ніж шкала Хаббла. Спочатку вони знаходяться в спокої щодо потоку Хаббла, і локально гравітаційних тіл немає. Як обговорювалося в прикладі 15, прискорення однієї тестової частинки щодо іншої задається\((\frac{\ddot{a}}{a}\)) r, де r - їх відносне зміщення.

Таким чином, якщо ми спостерігаємо будь-які ненульові ефекти розширення на локальній системі, вони насправді не є наслідками розширення взагалі, а наслідками прискорення розширення. Коефіцієнт\(\frac{\ddot{a}}{a}\) знаходиться на порядку оберненого квадрата віку Всесвіту, тобто H ² _{o ÷} 10 ⁻³⁵ s ⁻². Малість цього фактора - це те, що робить вплив на таку систему, як Сонячна система, настільки абсурдно крихітним.

Приклад 24: Тіло людини

Оцінимо вплив космологічного розширення на довжину L вашої кістки стегна. Тіло складається з атомів, і з причин, наведених раніше, не може бути стійкої тенденції розмірів цих атомів або довжин хімічних зв'язків між ними. Кістка відчуває стрес через космологічне розширення, але вона знаходиться в рівновазі, і деформація зникне, якщо гравітаційне напруження буде знято (наприклад, якщо інші гравітаційні напруги накладаються поверх космологічного, щоб скасувати його). Аномальне прискорення між кінцями кістки - (\(\frac{\ddot{a}}{a}\)) L, яке спостерігається як аномальне напруження. Беручи\(\frac{\ddot{a}}{a} \sim H^{2}_{o}\), аномальне прискорення одного кінця кістки щодо іншого - LH ². Відповідне стиснення або напруга - mLH ², де m - ваша маса тіла. Отриманий\(\epsilon\) штамм - це\(\frac{mLH^{2}}{AE}\), де E - модуль Юнга кістки (близько 10 ¹⁰ Па), а А - площа поперечного перерізу кістки.

Якщо поставити цифри, результат для деформації становить близько 10 ⁻⁴⁰, що є занадто малим, щоб його можна було виміряти будь-якою мислимою технікою, і насправді буде завалено іншими ефектами. Оскільки ознака a¨ в даний час позитивний, ця деформація розтягує, а не стискає. У більш ранню епоху Всесвіту, яка домінувала, вона була б стискаючою.

Немає «світської тенденції», тобто ваша кістка ноги з часом не розширюється. Він знаходиться в рівновазі, і просто витягнутий непомітно в порівнянні з довжиною, якби мав без ефекту космологічного розширення.

Приклад 25: штам на атомному ядрі

Оцінка в прикладі 24 також може бути застосована до атомного ядра, яке має ядерний «модуль Юнга» порядку 1 МеВ/FM ^{3 ÷} 10 ³² Па. В результаті виходить\(\epsilon\) штам 10 ⁻⁵².

Приклад 26: великий рип

Вважається, що відомі форми речовини мають рівняння стану P = w\(\rho\) з w ≥ −1. Значення всесвіту, де переважають у вакуумі, буде w = −1. Космологічні спостереження ²³ показують, що емпірично сучасний Всесвіт поводиться так, ніби він складається з речей з w = −1,03 ± 0,16, і це залишає відкритою можливість w < −1. У цьому випадку розв'язання рівнянь Фрідмана дає масштабний коефіцієнт a (t), який вибухає до нескінченності при якомусь скінченному t. при такому сценарії, відомому як «Великий Ріп»,\((\frac{d}{dt})(\frac{\ddot{a}}{a})\) розходиться, і будь-яка система, незалежно від того, наскільки щільно пов'язана, розривається на частини. ²⁴

---

²³ Карнеро та ін., arxiv.org/abs/1104.5426

²⁴ Колдуелл та ін., arxiv.org/abs/астро-ph/0302506

Приклади 24-26 показують, що крім гіпотетичних екстремальних космологічних умов, немає надії виявити будь-який вплив космологічного розширення на системи, виготовлені з конденсованого середовища. Нам потрібно подивитися на набагато більші системи, щоб побачити будь-який ефект, і такі системи утримуються гравітацією. Для конкретності продовжуємо говорити про систему земля-сонце. Мало того, що аномальна сила на землі мала, вона не гарантується виробляти жодної світської тенденції, яка, швидше за все, буде виявлена. Напрямок аномальної сили на землі назовні для прискорюючого космологічного розширення, як ми тепер знаємо, це стосується нинішньої епохи. Як приклад, в якому немає світської тенденції, космологія, що домінує у вакуумі, дає постійне значення для\(\frac{\ddot{a}}{a}\), тому зовнішня сила постійна. Як і при впливі радіаційного тиску, існування цієї постійної, зовнішньої сили дуже майже еквівалентно масштабуванню гравітаційної сили сонця на крихітну кількість, тому рух все ще дуже майже кеплер, але з трохи «неправильною» константою пропорційності в законі періодів Кеплера. Таким чином, швидкість\(\dot{r}\) зміни радіуса кругової орбіти в цьому випадку дорівнює нулю.

Але в більшості космологій не\(\frac{\ddot{a}}{a}\) зовсім постійна, і аномальна сила на землі змінюється. У космології з домінуючою речовиною з\(\Lambda\) = 0, у фазі розширення сила всередині, але зменшується з часом, тому орбіта з часом розширюється. Те, що насправді важливо тоді, є\((\frac{d}{dt})(\frac{\ddot{a}}{a})\). Якби ми могли вибрати будь-яку функцію для a (t), ми могли б скласти приклади, в яких\(\dot{a}\) > 0 але\((\frac{d}{dt})(\frac{\ddot{a}}{a})\) < 0, так що Сонячна система реагувала на космологічне розширення скороченням!

Функція a (t), однак, повинна задовольняти рівняння Фрідмана, одне з яких є (в одиницях з G ≠ 1)

\[\frac{\ddot{a}}{a} = G \Big[ \dfrac{1}{3} \Lambda - \frac{4 \pi}{3} (\rho + 3P) \Big] \ldotp \tag{8.2.18} \]

Нинішня епоха Всесвіту, здається, добре моделюється темною енергією, описаною постійною\(\Lambda\) плюсовою пилом з P <<\(\rho\). Диференціація обох сторін щодо часу дає

\[\dfrac{d}{dt} \left(\dfrac{\ddot{a}}{a}\right) \propto \dot{\rho}, \tag{8.2.19} \]

з негативною константою пропорційності. Це гарантує, що знак ефекту завжди, як очікується від наївного маніхейського образу зв'язуючих сил, що борються проти космологічного розширення (або, можливо, співпрацюють під час фази контракту космології Big Crunch).

Одним із способів розуміння того, чому це так приємно зводиться до залежності від,\(\dot{\rho}\) є міркування, наведені в прикладі 15, в якому ми виявили, що відносне прискорення двох тестових частинок A і B в космології FRW, де домінують питання, можна точно розрахувати, роблячи вигляд, що це пов'язано з наявність пилу в будь-якій даній сфері S, що оточує дві частинки. Тепер ми дозволимо A бути сонцем, B землею, і S сферою з центром на сонці, радіус якого дорівнює радіусу кругової орбіти Землі. Завдяки космологічному розширенню пил всередині S з часом розріджується, зменшуючи її щільність\(\rho\). Застосування законів Ньютона до орбіти Землі дає\(\omega^{2} r = \frac{GM}{r^{2}}\), а збереження моменту моменту призводить до\(\omega\) r ² = const. Обчислення дає $\ frac {r} {r_ {o}} =\ frac {M + (\ frac {4\ pi} {3})\ rho_ {o} r^ {3} _ {o}}} {M + (\ frac {4\ pi} {3})\ rho r^ {3}}\ тег {8.2.20} $$, що призводить до\(\frac{\dot{r}}{r_{o}} \approx −(\frac{4 \pi}{3})G \omega^{−2}_{o} \dot{\rho}\). Застосування рівнянь Фрідмана дає

\[\frac{\dot{r}}{r_{o}} = \omega^{-2}_{o} \left(\dfrac{d}{dt}\right) \left(\frac{\ddot{a}}{a}\right), \tag{8.2.21} \]

який дійсний загалом, а не тільки для P = 0. \(\omega^{−2}_{o}\)Фактор показує, що ефект менший для більш щільно пов'язаних систем.

Ми знаємо, що Всесвіт в теперішню епоху має\((\frac{d}{dt})(\frac{\ddot{a}}{a})\) > 0, тому що\(\dot{\rho}\) < 0, і для цілей оцінки порядку величини ми можемо взяти\((\frac{d}{dt})(\frac{\ddot{a}}{a}) \sim H^{3}_{o}\). Підключивши цифри для системи земля-сонце, ми виявляємо, що з епохи динозаврів радіус земної орбіти виріс менше діаметра атомного ядра. ²⁵

Примітка

Мальовниче зображення походить від Cooperstock et al., http://arxiv.org/abs/astro-ph/9803097v1, які дають інший розрахунок, що призводить до результату для\(\dot{r}\) точно еквівалентного отриманому тут.

Спостереження

Історично вважалося, що космологічна константа дорівнює нулю, що майже вся матерія у Всесвіті була у формі атомів, і тому існує лише один цікавий космологічний параметр для вимірювання, який був середньою щільністю речовини. Цю щільність було дуже важко визначити, навіть в межах порядку, тому що більша частина матерії у Всесвіті, ймовірно, не випромінює світло, що ускладнює його виявлення. Астрономічні шкали відстані також були дуже погано відкалібровані проти абсолютних одиниць, таких як СІ. Однак, починаючи приблизно з 1995 року, новий набір методів призвів до ери високоточної космології.

Просторова кривизна від коливань CMB

Сильне обмеження на моделі походить від точних вимірювань космічного мікрохвильового фону, особливо зондом COBE 1989-1993 та його наступником 2001-2009, мікрохвильовим анізотропічним зондом Вілкінсона, розташованим у точці L2 Лагранжа системи земля-сонце, за межами Землі на лінії, що з'єднує сонце і земля. ²⁶ Температура космічного мікрохвильового фонового випромінювання не однакова у всіх напрямках, і вимірювати її можна під різними кутами. У Всесвіті з негативною просторовою кривизною сума внутрішніх кутів трикутника менше евклідової величини 180 градусів. Тому, якщо ми спостерігаємо зміну CMB за деяким кутом, відстань між двома точками на поверхні останнього розсіювання насправді більше, ніж було б виведено з евклідової геометрії. Шкала відстані таких варіацій обмежена швидкістю звуку в ранньому Всесвіті, тому можна працювати назад і робити висновок про просторову кривизну Всесвіту на основі кутової шкали анізотропій. Вимірювання просторової кривизни зазвичай викладені через параметр\(\Omega\), який визначається як загальна середня щільність всіх вихідних термінів у рівняннях поля Ейнштейна, розділених на критичну щільність, яка призводить до плоского Всесвіту. \(\Omega\)включає внесок матерії\(\Omega_{M}\), космологічної\(\Omega_{\Lambda}\) константи та випромінювання (незначний у сучасному Всесвіті). Результати з WMAP в поєднанні з іншими даними інших методів дають\(\Omega\) = 1,005 ± 0,006. Іншими словами, Всесвіт дуже майже просторово плоский.

Малюнок\(\PageIndex{6}\) - Кутова шкала коливань космічного мікрохвильового фону може бути використана для виведення кривизни Всесвіту.

Прискорення розширення від наднових даних

Дані наднових, описані в розділі 8.2, доповнюють дані CMB, оскільки вони в основному чутливі до різниці\(\Omega_{\Lambda} − \Omega_{M}\), а не до їх суми\(\Omega = \Omega_{\Lambda} + \Omega_{M}\). Це пов'язано з тим, що ці дані вимірюють прискорення або уповільнення розширення Всесвіту. Матерія виробляє уповільнення, тоді як космологічна константа дає прискорення. На малюнку 8.2.7 показані деякі останні дані про наднові. ²⁷ Горизонтальна вісь дає коефіцієнт червоного зсуву z =\(\frac{\lambda' − \lambda}{\lambda}\), де довжина хвилі,\(\lambda'\) що спостерігається на землі, і\(\lambda\) довжина хвилі спочатку випромінюється. Він вимірює, наскільки швидко галактика наднової відступає від нас. Вертикальна вісь\(\Delta\) (M−m) = (M−m) − (m−m) _{порожня}, де m - видима величина, M - абсолютна величина, а (m − M) _{порожня} - значення, очікуване у моделі порожнього Всесвіту, з\(\Omega\) = 0. Різниця m−m є мірою відстані, тому по суті це графік відстані та швидкості рецесії, такого ж загального типу, який використовував Хаббл у своєму первісному відкритті розширення Всесвіту. Віднімання (m−m) _{порожнього} на вертикальній осі полегшує видимість малих відмінностей. Оскільки дані WMAP вимагають\(\Omega\) = 1, ми повинні відповідати дані наднових зі значеннями\(\Omega_{M}\) і\(\Omega_{\Lambda}\) які складаються до одиниці. Спроба зробити це з\(\Omega_{M}\) = 1 і\(\Omega_{\Lambda}\) = 0 явно не відповідає даними, тому можна зробити висновок, що космологічна константа, безумовно, позитивна.

Малюнок\(\PageIndex{7}\) - Змова Хаббла для далеких наднових. Кожна точка даних являє собою середнє значення над кількома різними надновими з майже однаковим z.

Щільність речовини від баріонних акустичних коливань

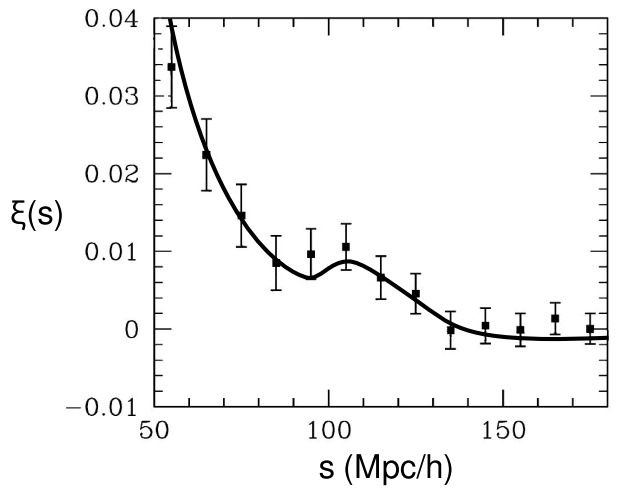
Такі зусилля, як Sloan Digital Sky Survey, зробили тривимірні карти щільності світиться речовини у Всесвіті. ²⁸ Розподіл незграбний. Вимірюючи середню кореляцію\(\xi\) між щільністю в точках, розділених деякою відстанню s\(\xi\) (вимірюється в сполучній рамці), можна було б очікувати, що функція (и) буде найбільшою, коли s була маленькою і просто звужується зі збільшенням s. стиль пейзаж хмарочосів пліч-о-пліч з безлюдною гірською пустелею. З іншого боку, уявіть собі таку кореляційну функцію для будинків у підрозділі, в якому дороги не утворюють жодної регулярної сітки, але правила зонування забороняють будівництво будинків на ділянках менше певного розміру. У цій ситуації існувала б нульова ймовірність знаходження будинків, розділених дуже малими відстанями, і\(\xi\) (и) буде демонструвати пік у деякому більшому масштабі, встановленому правовим кодексом. Фактичні результати зйомок неба показують такий пік, який обумовлений добре відомою фізикою, яку називають баріонними акустичними коливаннями (BAO). ²⁹ У ранньому Всесвіті будь-яка область надмірної щільності, як правило, створює випромінюючу звукову хвилю, подібну до вибуху петарди. Такі хвилі поширювалися з відомою швидкістю (близько половини швидкості світла) протягом відомого часу (близько 400 000 років, поки речовина не стала деіонізованою і прозорою для випромінювання, зробивши її несприйнятливою до фотонного тиску, що призвело до коливань). Це призводить до відомої відстані s, яка утворює стандартну лінійку, на якій відбувається пік в\(\xi\) (ах). У космологічних моделям ці результати сильно\(\Omega_{M}\) обмежують, будучи відносно нечутливими до\(\Omega_{\Lambda}\), і тому вони доповнюють як дані наднових, так і результати CMB.

Малюнок\(\PageIndex{8}\) - Акустичний пік у кореляційній функції BAO. Перемальовано з Ейзенштейна, Нові огляди астрономії. 49 (2005) 360, як відтворено в Бассетт і Хлозек, 2009, arxiv.org/abs/0910.5224.

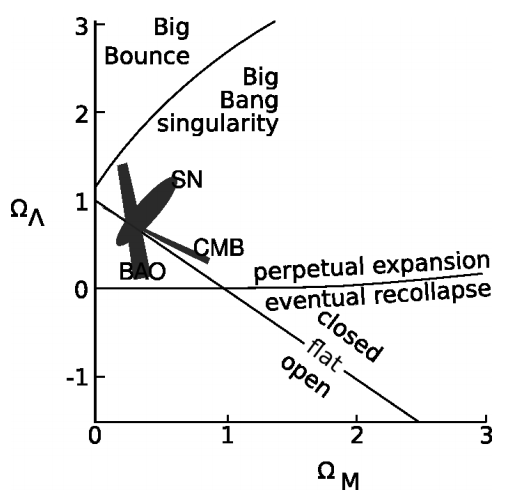
Висновки про космологію

Малюнок 8.2.9 узагальнює те, що ми можемо зробити висновок про наш Всесвіт, параметризовану з точки зору моделі з обома\(\Omega_{M}\) і\(\Omega_{\Lambda}\) ненульовими. ³⁰ Ми можемо сказати, що вона виникла в особливості Великого вибуху, що вона продовжуватиме розширюватися назавжди, і що вона дуже майже рівна. Зауважте\(\Omega_{\Lambda}\), що в космології з ненульовими значеннями для обох\(\Omega_{M}\) і немає суворого зв'язку між просторовою кривизною та питанням повторного колапсу, оскільки в моделі є лише матерія і без космологічної константи; тому, хоча ми знаємо, що Всесвіт не повернеться, ми не знають, чи є його просторова кривизна трохи позитивна (замкнута) або негативна (відкрита).

Малюнок\(\PageIndex{9}\) - Космологічні параметри нашого Всесвіту, після Перлмуттера, 1998, arxiv.org/abs/astro-ph/9812133 і Ковальського, 2008, arxiv.org/abs/0804.4142. Три затінені області представляють 95% областей довіри для трьох типів спостережень.

Перевірки узгодженості

Астрофізичні міркування забезпечують подальші обмеження та перевірки узгодженості. В епоху до появи високоточної космології оцінки віку Всесвіту коливалися від 10 мільярдів до 20 мільярдів років, а низький кінець був неузгоджений з віком найдавніших кулястих скупчень. Вважалося, що це проблема або для спостережної космології, або для астрофізичних моделей, що використовуються для оцінки віку кластерів: «Ви не можете бути старшими за свою ма». Поточні дані показали, що низькі оцінки віку були невірними, тому послідовність відновлюється.

Те, що лише мала частина речовини Всесвіту була світлою, підозрювали астрономи, такі як Цвікі, ще в 1933 році, грунтуючись на нездатності узгодити спостережувану кінематику з законами Ньютона, якщо вся матерія вважалася світлою.

Темна матерія

Ще одне обмеження походить від моделей нуклеосинтезу в епоху незабаром після Великого вибуху (до утворення перших зірок). Спостережувана відносна кількість водню, гелію та дейтерію не може бути узгоджена з щільністю «пилу» (тобто нерелятивістської речовини), виведеною з даних спостережень. Якщо виведена масова щільність була повністю обумовлена нормальною «баріонної» речовиною (тобто речовиною, маса якої складалася в основному з протонів і нейтронів), то ядерні реакції в щільному ранньому Всесвіті повинні були протікати відносно ефективно, приводячи до набагато більш високого співвідношення гелію до водню, і набагато нижче велика кількість дейтерію. Висновок полягає в тому, що більша частина матерії у Всесвіті повинна бути зроблена з невідомого типу екзотичної небаріонної речовини, відомої загалом як «темна матерія».

Існування небаріонної речовини також потрібно для узгодження спостережуваної щільності галактик із спостережуваною силою флуктуацій CMB, а в зливаються скупченнях галактик спостерігалося, що гравітаційний потенціал зміщується від випромінюючої плазми. Огляд 2012 року з темної матерії є Roos, arxiv.org/abs/1208.3662.

Проводиться ряд експериментів для безпосереднього виявлення темної матерії. Станом на 2013 рік найбільш чутливий експеримент дав нульові результати: arxiv.org/abs/1310.8214.

Свого часу широко очікувалося, що темна матерія буде складатися з найлегшої суперсиметричної частинки, яка, наприклад, може бути нейтраліно. Однак результати LHC, здається, роблять малоймовірним, що наш Всесвіт демонструє суперсиметрію, припускаючи, що енергетична шкала - це електрослабкі масштаби, що є єдиною шкалою, яка має сильну мотивацію. Зараз більш імовірно, що темна матерія складається з якоїсь іншої частинки, такої як стерильні нейтрино або аксіони. Навіть при включенні темної матерії виникає проблема з великою кількістю літію-7 щодо водню, що моделі сильно перепрогнозують. ³¹

Посилання

²⁶ Комацу та співавт., 2010, arxiv.org/abs/1001.4538

²⁷ Рієс та співавт., 2007, arxiv.org/abs/астро-ph/0611572. Більший набір даних аналізується в Kowalski et al., 2008, arxiv.org/abs/0804.4142.

²⁸ Санчес та ін., 2012, arxiv.org/abs/1203.6616

²⁹ Бассетт і Хлозек, 2009, arxiv.org/abs/0910.5224

³⁰ Дивіться Керролл, «Космологічна константа» http://www.livingreviews.org/lrr-2001-1 для повної математичної обробки таких моделей.

³¹ arxiv.org/абс/08.08.2818, arxiv.org/abs/1107.1117