6.6: Вироджені розчини

Цей розділ можна опустити при першому читанні.

На горизонті подій просторового часу Шварцшильда часові та просторові ролі Шварцшильда\(r\) та\(t\) координат змінюються місцями, так що знаки у метриці змінюються від +−−− до − + −−. При обговоренні подібних випадків стає зручним визначити нове вживання терміна «підпис», як s = p − q, де p — кількість позитивних знаків, а q — кількість негативних. Це також може бути представлено парою чисел (p, q). Приклад горизонту Шварцшильда не надто тривожний, як тому, що смішна поведінка виникає при сингулярності, яку можна видалити зміною координат, так і тому, що підпис залишається незмінним. Спостерігач, який вільно падає через горизонт, зауважує, що локальні властивості простору-часу залишаються незмінними, з |s| = 2, як того вимагає принцип еквівалентності.

Але це лише змушує нас задатися питанням, чи є інші приклади, в яких спостерігач фактично виявить зміну підпису метрики. Нам рекомендується думати про підпис як щось емпірично спостережуване, оскільки, наприклад, було запропоновано, що наш Всесвіт може мати раніше несподівані додаткові космічні розміри, і ці теорії роблять перевірені прогнози. Оскільки ми не помічаємо зайвих розмірів в звичайному житті, їх довелося б загорнути в циліндричну топологію. Деякі такі теорії, як теорія струн, є спробами створити теорію квантової гравітації, тому циліндричний радіус вважається на порядку довжини Планка, що відповідає квантово-механічно енергетичній шкалі, яку ми не зможемо дослідити за допомогою будь-якої передбачуваної технології. Але також можливо, що радіус великий - можливість, яка йде під назвою «великі додаткові розміри» - так що ми могли побачити ефект на Великому адронному колайдері. Ніщо в формулюванні рівнянь поля Ейнштейна не вимагає підпису 3+1 (тобто (1, 3)), і вони працюють однаково добре, якщо підпис замість 4+1, 5+1,. Зворотно-квадратний закон гравітації Ньютона описується загальною відносністю як випливає з тривимірної природи простору, тому на малих масштабах в теорії з n великими додатковими розмірами поведінка 1/r ² змінюється на 1/r ²⁺ⁿ, і стає можливим, що LHC може виробляти мікроскопічні чорні діри, які б негайно випаровувалися в випромінювання Хокінга характерним чином.

Отже, виявляється, що підпис простору-часу - це те, що апріорі не піддається пізнанню, і його потрібно визначати експериментом. Коли річ повинна бути експериментально спостережуваною, загальна відносність говорить нам, що вона краще була незалежною від координат. Чи так це? Пропозиція з лінійної алгебри під назвою закон інерції Сильвестра спонукає нас вірити, що це так. Теорема стверджує, що при діагоналізації дійсної матриці\(A\) дійсною, несингулярною зміною базису (перетворення подібності S ⁻¹ AS) однозначно визначається кількість позитивних, негативних та нульових діагональних елементів. Оскільки зміна координат впливає на застосування перетворення подібності до метрики, виявляється, що підпис є координатно-незалежною.

Це не зовсім правильно, однак, як показує наступний парадокс. Координатна інваріантність загальної відносності говорить нам, що якби всі годинники, всюди у Всесвіті, сповільнювалися одночасно (з одночасністю, визначеною будь-яким способом, який нам подобається), не було б спостережуваних наслідків. З цього випливає, що простору/час

\[ds^2 = −t \,dt^2 − d \ell^{2},\]

де

\[d \ell^{2} = dx^2 + dy^2 + dz^2,\]

емпірично не відрізняється від плоского просторучасу. Починаючи з t =\(− \infty\), позитивна складова g _tt метрики рівномірно стискається, що повинно бути нешкідливим. Ми дійсно можемо перевірити шляхом прямої оцінки тензора Рімана, що це плоский простор-час (проблема 10). Але для t > 0 підпис метрики переходить з + − −− на − − −−, тобто з Лоренціанського (|s| = 2) на евклідову (|s| = 4). Це викликає занепокоєння. Для t < 0 метрика є цілком коректним описом нашого власного Всесвіту (який приблизно плоский). Час минає, і немає ніяких ознак будь-якої насувається катастрофи. Потім, раптом, в якийсь момент часу вся структура просторучасу піддається жахливому спазму. Це парадокс, тому що ми могли б також поставити свої початкові умови, використовуючи іншу систему координат, в якій метрика мала звичну форму ds ² = dt ² −d\(\ell^{2}\). Загальна відносність повинна бути агностичною щодо координат, але вибір координат призводить до різного прогнозу про сигнатуру, яка є координатно-незалежною величиною.

Нас призводять до вирішення парадоксу, якщо ми явно побудуємо координатне перетворення. У координатах (t, x, y, z) ми маємо ds ² = −t dt ² − d\(\ell^{2}\). Ми хотіли б знайти зв'язок між t та деякою іншою координатою u таким чином, щоб ми відновили звичну форму ds ² = du ² −d\(\ell^{2}\) для метрики. Закон тензорного перетворення дає

\[\begin{split} g_{tt} &= \left(\dfrac{\partial u}{\partial t}\right)^{2} g_{uu} \\ -t &= \left(\dfrac{\partial u}{\partial t}\right)^{2} \end{split}\]

з розчином

\[u = \pm \frac{2}{3} t^{\frac{3}{2}}, \quad t < 0 \ldotp\]

Немає рішення для t > 0.

Малюнок\(\PageIndex{1}\) - Зміна координат вироджується при t = 0.

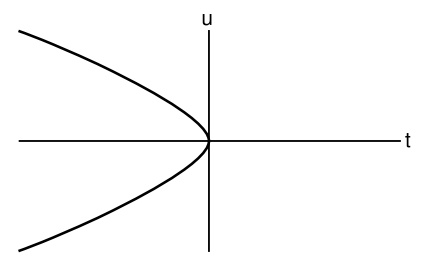
Якщо фізики, що живуть у цьому Всесвіті, при t < 0, чомусь вибирають t як свою часову координату, насправді є спосіб сказати, що катаклізматична подія при t = 0 не є достовірним прогнозом. При t = 0 часова складова їх метрики зникає, тому її підпис змінюється з + − −− на 0 − −−. У цей момент ламається механізм стандартної тензорної постановки загальної теорії відносності. Наприклад, більше не можна піднімати індекси, тому що g ^ab - матриця, обернена g _ab, але g _ab не є оборотною. Оскільки польові рівняння в кінцевому підсумку виражаються через метрику за допомогою машин, що включає підвищення та зниження індексів, немає можливості застосувати їх при t = 0. Вони не роблять помилкового пророкування кінця світу; вони взагалі не роблять жодного прогнозу. Фізики, які звикли працювати з точки зору t координати, можуть просто підкинути руки і сказати, що у них немає можливості передбачити що-небудь при t > 0. Але вони вже знають, що їх просторовийчас - це той, чиї спостережувані, такі як кривизна, є постійними щодо часу, тому вони повинні запитати, чому ця ідеальна симетрія порушена, виділивши t = 0. Фізично немає нічого, що повинно зробити один момент часу відмінним від будь-якого іншого, тому вибір певного часу для виклику t = 0 слід інтерпретувати просто як довільний вибір розміщення походження системи координат. Це говорить про те, що всі проблеми, які вони мали, - це не проблеми з будь-яким фізичним змістом, а лише проблеми, що виникають внаслідок поганого вибору координат. Вони виконують розрахунок вище, і виявляють координату часу u. Виражена в терміні u, метрика добре себе веде, і механізм прогнозування ніколи не ламається.

Парадокс, поставлений раніше, вирішується, оскільки закон інерції Сильвестра застосовується лише до несингулярного перетворення S. Якби S був сингулярним, то S ⁻¹, про який йдеться у теоремі, навіть не існувало б. Але перетворення від u до t має\(\frac{\partial t}{\partial u}\) = 0 при u = t = 0, тому воно є одниною. Це все відповідає загальній філософії координатно-інваріантності в відносності, яка полягає в тому, що допускаються лише плавні перетворення координат один до одного. Той, хто знайшов щасливу координату, як у, і хто потім розглядає перетворення на t, повинен усвідомити, що це не гарна ідея, тому що трансформація не є гладкою і один-на-один. Хтось, хто почав працювати з невдалою координатою, як t, виявляє, що техніка ламається при t = 0, і робить висновок, що було б гарною ідеєю шукати більш корисний набір координат. Така ситуація реально може виникнути при практичних розрахунках.

А як щодо нашого оригінального запитання: чи може підпис простору-часу насправді змінитися на певній межі? Відповідь тепер зрозуміла. Така зміна підпису - це те, що, можливо, могло б мати внутрішній фізичний сенс, але якщо так, то стандартна формулювання загальної відносності не здатна робити прогнози з цього приводу. Існують інші формулювання загальної відносності, такі як Аштекар, які зазвичай еквівалентні Ейнштейну, але здатні робити прогнози щодо зміни підпису. Однак існує не одна така формулювання, і вони не погоджуються зі своїми прогнозами щодо зміни підпису.