6.2: Метрика Шварцшильда (частина 1)

Тепер ми поставили перед собою мету знайти метрику, що описує статичний простор поза сферично симетричним, необертається тілом маси m, яке вперше було вирішено Карлом Шварцшильдом у 1915 році. ³ Одним побічним продуктом знаходження цієї метрики буде можливість точно розрахувати геодезичний ефект, але він матиме більш далекосяжні наслідки, в тому числі і існування чорних дір. Задача, яку ми розв'язуємо, подібна до обчислення сферично симетричного розв'язку закону Гаусса у вакуумі. Рішення електричної задачі має вигляд\(\dfrac{\hat{\textbf{r}}}{r^{2}}\), з довільною константою пропорційності, яка виявляється пропорційною заряду, що створює поле. Одна велика різниця, однак, полягає в тому, що в той час як закон Гаусса лінійний, рівняння

\[R_{ab} = 0\]

є дуже нелінійним, так що рішення не можна просто масштабувати вгору і вниз пропорційно\(m\).

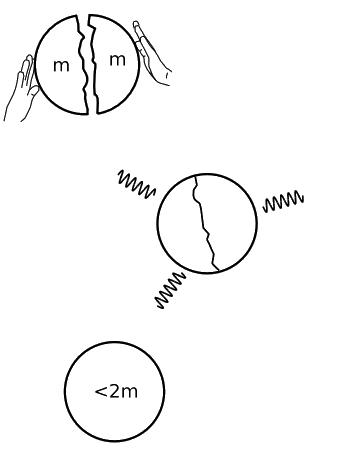
Причина такої нелінійності є основоположною для загальної теорії відносності. Наприклад, коли земля конденсувалася з споконвічної сонячної туманності, вироблялися великі обсяги тепла, і ця енергія потім поступово випромінювалася в космічний простір, зменшуючи загальну масу землі. Якщо робити вигляд, як на рис.\(\PageIndex{1}\), що цей процес передбачав злиття всього двох тіл, кожне з масою m, то чистий результат був по суті прийняти відокремлені маси m і m в спокої, і зблизити їх до утворення близькосусідських мас m і m, знову в спокої. Кількість енергії, що випромінюється, була пропорційна м ², тому гравітаційна маса комбінованої системи була зменшена від\(2m\) до\(2m−(. . .)m^2\), де.. є приблизно\(\dfrac{G}{c^{2} r}\). Існує нелінійна залежність гравітаційного поля від мас.

Малюнок\(\PageIndex{1}\): Польові рівняння загальної теорії відносності нелінійні.

Вправа\(\PageIndex{1}\)

Підпис метрики визначається як перелік позитивних і негативних знаків, що виникають при її діагоналізації. ⁴ Принцип еквівалентності вимагає, щоб підпис був + − −− (або − + ++, залежно від вибору знакових умовностей). Переконайтеся, що будь-яка постійна метрика (включаючи метрику з «неправильним» підписом, наприклад, розміри 2+2, а не 3+1) є рішенням рівняння поля Ейнштейна у вакуумі.

---

⁴ Див. Розділ 6.3 для іншого, але тісно пов'язаного використання одного і того ж терміну.

Принцип відповідності говорить нам, що наш результат повинен мати ньютонівську межу, але єдині змінні, що беруть участь, - m і r, тому ця межа повинна бути тією, в якій\(\dfrac{r}{m}\) велика. Великий в порівнянні з чим? Немає нічого іншого, з яким можна порівнювати, тому він може бути лише великим порівняно з деяким виразом, що складається з безіменних констант G і c., Ми вже вибрали такі одиниці\(c = 1\), що, і тепер ми\(G = 1\) також встановимо. Маса і відстань тепер можна порівняти, причому коефіцієнт перетворення становить\(\dfrac{G}{c^{2}} = 7 \times 10^{^−28} \,m/kg\), або близько милі на сонячну масу. Оскільки радіус Землі в тисячі разів більше, ніж миля, а його маса в сотні тисяч разів менше, ніж у Сонця, він\(\dfrac{r}{m}\) дуже великий, і ньютонівське наближення досить добре для всіх, крім найбільш точних додатків, таких як мережа GPS або експеримент Gravity Probe B.

Справа з нульовою масою

Спочатку давайте продемонструємо тривіальне рішення з плоским просторомчасу. У сферичних координатах ми маємо

\[ds^{2} = dt^{2} - dr^{2} - r^{2} \theta^{2} - r^{2} \sin^{2} \theta d \phi^{2} \ldotp\]

Незникаючі символи Крістоффеля (ігноруючи свопи нижчих індексів):

\[\begin{split} \Gamma^{\theta}_{r \theta} &= \dfrac{1}{r} \\ \Gamma^{\phi}_{r \phi} &= \dfrac{1}{r} \\ \Gamma^{r}_{\theta \theta} &= -r \\ \Gamma^{r}_{\phi \phi} &= -r \sin^{2} \theta \\ \Gamma^{\theta}_{\phi \phi} &= \sin \theta \cos \theta \\ \Gamma^{\phi}_{\theta \phi} &= \cot \theta \end{split}\]

Вправа\(\PageIndex{2}\)

Якби ми використовували метрику (− + ++) замість (+ − −−), що б вплинуло на символи Крістоффеля? Що робити, якщо ми висловили метрику в різних одиницях, масштабуючи всі координати множником k?

Використання тензора c

Насправді, коли я розрахував символи Крістоффеля вище вручну, я отримав один з них неправильно, і пропустив обчислення один одного, тому що я думав, що це нуль. Я знайшов свою помилку лише порівнявши результат у підручнику. Обчислення тензора Рімана - це ще більший безлад. Тут явно непогано вдатися до системи комп'ютерної алгебри. Кадабра, про яку йшла мова раніше, спеціально розроблена для координатно-незалежних розрахунків, тому тут не допоможе. Непоганим безкоштовним і відкритим вихідним кодом вибором є ctensor, який є одним із стандартних пакетів, розповсюджених разом з системою комп'ютерної алгебри Maxima, представленої в розділі 2.5.

Наступна програма Maxima обчислює знайдені раніше символи Крістоффеля.

Рядок 1 завантажує пакет тензора. Рядок 2 встановлює назви координат. Рядок 3 визначає g _ab, причому 1g означає «версію g з нижчими індексами». Рядок 7 говорить Maxima виконати деяку настройку роботи з g _ab, включаючи обчислення зворотної матриці g ^ab, яка зберігається в ug. Лінія 8 говорить, щоб обчислити символи Крістоффеля. Позначення mcs відноситься до тензора\(\Gamma'^{a}_{bc}\) з індексами, поміняними навколо трохи порівняно з конвенцією, що\(\Gamma^{a}_{bc}\) дотримується в цій книзі. У системі Linux ми поміщаємо програму в файл flat.mac і запускаємо її за допомогою команди maxima -b flat.mac. Відповідна частина вихідних даних:

Додавання команди ricci (true); в кінці програми призводить до виведення THIS SPACETIME IS EMPTY І/АБО FLAT, що економить нам години нудних обчислень. Обчислюється тензор ric (який тут буває нульовим), і всі його ненульові елементи друкуються. Існує аналогічна команда riemann (true); для обчислення Riemann rensor riem. Це зберігається так, що riem [i, j, k, l] є те, що ми б називали R ^л _ікж. Зверніть увагу, що l переміщується до кінця, а j і k також міняються місцями.

Геометризовані одиниці

Якщо маса, що створює гравітаційне поле, не дорівнює нулю, то нам потрібно вирішити, в яких одиницях його виміряти. Це вже виявилося дуже зручним для прийняття одиниць з\(c = 1\), і тепер ми також встановимо гравітаційну константу\(G = 1\). Раніше, з тільки c встановленим в 1, одиниці часу і довжини були однаковими, [T] = [L], і так були одиниці маси і енергії, [M] = [E]. При G = 1 всі вони стають однаковими одиницями:

\[ [T] = [L] = [M] = [E].\]

Вправа\(\PageIndex{3}\)

Перевірте це твердження, об'єднавши закон гравітації Ньютона з другим законом руху Ньютона.

Отриману систему називають геометризованою, оскільки такі одиниці, як маса, яка раніше належала до провінції механіки, тепер вимірюються за допомогою тих самих одиниць, які ми використовували б для геометрії.

Великий R ліміт

Тепер давайте подумаємо про те, як вирішити реальну проблему знаходження неплоскої метрики. Хоча загальна відносність дозволяє нам вибирати будь-які координати, які нам подобаються, сферична симетрія задачі передбачає використання координат, які використовують цю симетрію. Координати плоского простору\(\theta\) і все ще\(\phi\) можуть бути визначені однаково, і вони мають однакову інтерпретацію. Наприклад, якщо ми скинемо тестову частинку до маси з якоїсь точки простору, її світова лінія матиме постійну\(\theta\) і\(\phi\). Координата r трохи відрізняється. У криволінійному просторучасі окружність кола не дорівнює 2\(\pi\) рази відстані від центру до кола; насправді, розбіжність між цими двома по суті є визначенням кривизни Річчі. Це дає нам вибір двох логічних способів визначення r. Ми визначимо його як окружність, поділену на 2\(\pi\), що має ту перевагу, що останні два члени метрики такі ж, як у плоскому просторі:

\[−r^2d\theta^{2} −r^2 \sin^2 \theta\, d \phi^{2}.\]

Оскільки ми шукаємо статичні розв'язки, жоден з елементів метрики не може залежати від t. Крім того, рішення буде симетричним під t → −t, і\(\phi \rightarrow − \phi\), отже\(\theta \rightarrow − \theta\), ми не можемо мати жодних елементів поза діагоналлю. ⁵ Результат полягає в тому, що ми звузили метрику до чогось виду

\[ds^{2} = h(r) dt^{2} - k(r) dr^{2} - r^{2} d \theta^{2} - r^{2} \sin^{2} \theta d \phi^{2},\]

де h і k наближаються до 1 для r →\(\infty\), де просторово-час є плоским.

⁵ Докладніше про симетрію зворотного часу див. Пізніше.

Для керівництва, як побудувати h і k, давайте розглянемо прискорення тестової частинки в\(r \gg m\), який ми знаємо, як бути\(− \dfrac{m}{r^{2}}\), оскільки там застосовується нерелятивістська фізика. У нас є

\[\nabla_{t} v^{r} = \partial_{t} v^{r} + \Gamma^{r}_{tc} v^{c} \ldotp\]

Спостерігач вільно падає разом з частинкою спостерігає його прискорення рівним нулю, а тензор, який дорівнює нулю в одній системі координат, дорівнює нулю у всіх інших. Оскільки коваріантна похідна є тензором, ми робимо висновок, що\(\nabla_{t} v^{r}\) = 0 у всіх системах координат, включаючи (t, r,.) систему, яку ми використовуємо. Якщо частинка звільняється від спокою, то спочатку її швидкість чотиривекторна дорівнює (1, 0, 0, 0), тому знаходимо, що її прискорення в координатах (t, r) дорівнює\(− \Gamma^{r}_{tt} = − \dfrac{1}{2} g^{rr} \partial_{r} g_{tt} = − \dfrac{1}{2} \dfrac{h'}{k}\). Встановивши це рівне\(− \dfrac{m}{r^{2}}\), знаходимо\(\dfrac{h'}{k} = \dfrac{2m}{r^{2}}\) для r >> m Оскільки k ≈ 1 для великого r, ми маємо

\[h' \approx \dfrac{2m}{r^{2}} \; for \; r >> m \ldotp\]

Тлумачення цього розрахунку виглядає наступним чином. Ми стверджуємо принцип еквівалентності, за яким прискорення вільно падаючої частинки можна сказати нулем. Після деяких розрахунків виявимо, що швидкість, з якою час тече (закодована в h), не є постійною. Він різний для спостерігачів на різній висоті в гравітаційній потенційній ямі. Але це те, що ми вже вивели, без індексної гімнастики, на прикладі 7.

Інтегруючи, ми знаходимо, що для великих r, h = 1 −\(\dfrac{2m}{r}\).

Комплексне рішення

Рішення серії A

Ми дізналися деякі цікаві речі, але у нас все ще є надзвичайно неприємне нелінійне диференціальне рівняння для вирішення. Один із способів атакувати диференціальне рівняння, коли ви не уявляєте, як діяти, - це спробувати послідовне рішення. У нас є невеликий параметр,\(\dfrac{m}{r}\) щоб розширити навколо, так що давайте спробуємо написати h і k як ряд форми

\[h = \sum_{n = 0}^{\infty} a_{k} \left(\dfrac{m}{r}\right)^{n}\]

\[k = \sum_{n = 0}^{\infty} b_{k} \left(\dfrac{m}{r}\right)^{n}\]

Ми вже знаємо ₀, a ₁ і b ₀. Спробуємо знайти б ₁. У наступному коді Maxima я опускаю множник m в h ₁ для зручності. Іншими словами, ми шукаємо рішення для m = 1.

Я не буду відтворювати весь вихід тензора Річчі, який є об'ємним. Ми хочемо, щоб всі чотири його компоненти, що не зникають, щоб зникнути якомога швидше для великих значень r, тому я вирішив возитися з R _tt, який виглядав так само просто, як будь-який з них. Здається, він змінюється як r ⁻⁴ для великих r, тому давайте оцінимо\(\lim_{r \rightarrow \infty} (r^{4} R_{tt})\):

Результат є\(\dfrac{(b_{1}−2)}{2}\), так що давайте встановимо b ₁ = 2. Приблизне рішення, яке ми знайшли до цих пір (повторне вставлення m),

\[ds^{2} \approx \left(1 - \dfrac{2m}{r}\right) dt^{2} - \left(1 + \dfrac{2m}{r}\right) dr^{2} - r^{2} d \theta^{2} - r^{2} \sin^{2} \theta d \phi^{2},\]

був вперше виведений Ейнштейном в 1915 році, і він використовував його для вирішення проблеми некеплерівської релятивістської корекції до орбіти Меркурія, яка була одним з перших емпіричних тестів загальної відносності.

Продовжуючи в цій моді, результати такі:

$\ почати {спліт} a_ {0} &= 1\\ a_ {1} &= -2\\ a_ {2} &= 0\\ a_ {3} &= 0\\ кінець {спліт} $$

$\ почати {спліт} b_ {0} &= 1\\ b_ {1} &= 2\\ b_ {2} &= 4\\ b_ {2} &= 8\ кінець {спліт} $$

Рішення закритої форми

Рішення несподівано просте, і його можна викласти в закриту форму. Приблизний результат, який ми знайшли для h, насправді був точним. Для k у нас є геометричний ряд\(\dfrac{1}{(1 − \dfrac{2}{r})}\), і коли ми знову вставляємо множник m єдиним способом, який змушує одиниці працювати, ми отримуємо\(\dfrac{1}{(1 − \dfrac{2m}{r})}\). Результат для метрики

\[ds^{2} = \left(1 - \dfrac{2m}{r}\right) dt^{2} - \left(\dfrac{1}{1 - \dfrac{2m}{r}}\right) dr^{2} - r^{2} d \theta^{2} - r^{2} \sin^{2} \theta d \phi^{2} \ldotp\]

Це називається метрикою Шварцшильда. Швидкий розрахунок в Maxima демонструє, що це точне рішення для всіх r, тобто тензор Річчі зникає скрізь, навіть при r < 2m, що знаходиться поза радіусом збіжності геометричного ряду.

Симетрія зворотного часу

Метрика Шварцшильда є інваріантною при зміні часу, оскільки час відбувається лише у формі\(dt^2\), яка залишається незмінною при dt → − dt. Це та сама симетрія зворотного часу, яка виникає в ньютонівській гравітації, де поле описується гравітаційним прискоренням g, а прискорення - інваріантними у часі.

По суті, це приклад координатної незалежності загальної відносності. Закони фізики, забезпечені загальною відносністю, такі як рівняння вакуумного поля, є інваріантними при будь-якому плавному перетворенні координат, а t → −t є таким координатним перетворенням, тому загальна відносність має часово-зворотну симетрію. Оскільки метрика Шварцшильда була знайдена шляхом накладання часово-реверсивно-симетричних граничних умов на диференціальне рівняння часу, то вона є однаково дійсним рішенням, коли ми змінюємо час. Крім того, ми очікуємо, що метрика буде інваріантною під час зміни часу, якщо не відбудеться спонтанне порушення симетрії (див. Розділ 8.2).

Це говорить про те, що ми задаємо більш фундаментальне питання про те, які глобальні симетрії має загальна відносність. Чи має він симетрію при інверсії парності, наприклад? Або ми можемо взяти будь-яке рішення, таке як простір Шварцшильда, і перетворити його на систему відліку, в якій джерело поля рухається рівномірно в певному напрямку? Оскільки загальна відносність локально еквівалентна спеціальній відносності, ми знаємо, що ці симетрії є локально дійсними. Але, можливо, навіть не вийде визначити відповідні глобальні симетрії. Наприклад, є деякі просторичасу, на яких навіть неможливо визначити глобальну часову координату. На такому просторічасі, який описується як не орієнтований на час, не існує жодного гладкого векторного поля, яке всюди схоже на час, тому неможливо визначити минулі та майбутні світлові конуси у всіх точках простору, не маючи переривчастих змін у визначенні, що відбувається десь. Це схоже на те, як смуга Мебіуса не дозволяє глобально визначити орієнтацію її поверхні (напрямок «вгору», як бачить мураха).

Припустимо, що наш просторовий час орієнтований на час, і ми можемо визначити координати (p, q, r, s) таким чином, що p завжди є часовою координатою. Оскільки q → −q є плавним перетворенням координат, ми гарантуємо, що наш просторовий час залишається дійсним рішенням рівнянь поля при цій зміні. Але це не означає, що ми знайшли симетрію при інверсії парності в площині. Наша координата q не обов'язково інтерпретується як відстань вздовж певної «осі q». Такі осі навіть не існують глобально в загальній теорії відносності. Координата навіть не повинна мати одиниць часу або відстані; це може бути кут, наприклад, або взагалі не мати жодного геометричного значення. Аналогічно, ми могли б зробити перетворення q → q' = q + kp. Якщо ми думаємо про q як про вимірювання просторового положення та p часу, то це виглядає як перетворення Галілея, з k - швидкість. Розв'язок польових рівнянь, отриманих після виконання цього перетворення, все ще є дійсним рішенням, але це не означає, що відносність має симетрію Галілея, а не симетрію Лоренца. Немає розумного способу визначити перетворення Галілея, що діє на весь просторовий час, тому що, коли ми говоримо про перетворення Галілея, ми припускаємо існування таких речей, як глобальні координатні осі, які навіть не існують у загальній теорії відносності.

Посилання

³ «Про гравітаційне поле точкової маси згідно з теорією Ейнштейна», Sitzungsberichte der Koniglich Preussischen Akademie der Wissenschaften 1 (1916) 189. Переклад англійською мовою доступний за адресою http://arxiv.org/abs/physics/9905030v1.