2.9: Ескіз кривої
- Page ID
- 60383
У цьому розділі розглядаються деякі взаємодії між формою графіка\(f\) і поведінкою\(f'\). Якщо у нас є графік\(f\), ми побачимо, що ми можемо зробити висновок про значення\(f'\). Якщо ми знаємо значення\(f'\), то побачимо, що ми можемо зробити висновок про графік\(f\). Ми також будемо використовувати інформацію\(f''\), яку ми вивчаємо в останньому розділі.
Перша похідна інформація
Функція\(f(x)\) збільшується,\((a,b)\) якщо\(a \lt x_1 \lt x_2 \lt b\) має на увазі\(f( x_1 ) \lt f( x_2 )\).
Функція\(f(x)\) зменшується на\((a,b)\) якщо\(a \lt x_1 \lt x_2 \lt b\) має на увазі\(f( x_1 ) \gt f( x_2 )\).
Графічно збільшується (зменшується), якщо при русі зліва направо по графіку\(f\), висота графіка збільшується (зменшується).\(f\)
Ці ж ідеї мають сенс, якщо ми\(h(t)\) вважаємо висоту (у футах) ракети в\(t\) секундах часу. Ми природно говоримо, що ракета піднімається або що її висота збільшується, якщо висота\(h(t)\) збільшується протягом певного періоду часу, як\(t\) збільшується.
Перерахуйте інтервали, на яких показана функція збільшується або зменшується.

\(f\)збільшується на інтервалах [0,0,5], [2,3] і [4,6].
\(f\)зменшується на [0,5,2] і [6,8].
На інтервалі [3,4] функція не збільшується і не зменшується — вона постійна.
Для функції,\(f\) яка диференційована на інтервалі\((a,b)\);
- якщо\(f\) збільшується на\((a,b)\), то\(f'(x) \geq 0\) для всіх\(x\) в\((a,b)\).
- якщо\(f\) зменшується на\((a,b)\), то\(f'(x) \leq 0\) для всіх\(x\) в\((a,b)\).
- якщо\(f\) постійно\((a,b)\) увімкнено, то\(f'(x) = 0\) для всіх\(x\) в\((a,b)\).
Графік показує висоту вертольота протягом певного періоду часу. Намалюйте графік висхідної швидкості вертольота,\( \frac{dh}{dt} \).

Зверніть увагу, що\( h(t)\) має локальний максимум, коли\(t = 2 \) і\(t = 5\), і так\(v(2) = 0\) і\(v(5) = 0\). Аналогічно\(h(t)\) має локальний мінімум\(t = 3\), коли, так\(v(3) = 0\).
Коли\(h\) збільшується,\(v\) позитивний. Коли\(h\) зменшується,\(v\) є негативним.
Використовуючи цю інформацію, ми можемо накидати графік\(v(t) = \frac{dh}{dt}\).

Наступна теорема є майже зворотною теоремою Першої форми і пояснює зв'язок між значеннями похідної та графом функції з іншої точки зору. Він говорить про те, що якщо ми знаємо щось про значення\(f'\), то ми можемо зробити деякі висновки про форму графіка\(f\).
Для функції,\(f\) яка диференційована на інтервалі\(I\);
- якщо\(f'(x) \gt 0\) для всіх\(x\) в інтервалі\(I\),\(f\) то збільшується на\(I\).
- якщо\(f'(x) \lt 0\) для всіх\(x\) в інтервалі\(I\), то\(f\) зменшується на\(I\).
- якщо\(f'(x) = 0\) для всіх\(x\) в інтервалі\(I\), то\(f\) постійний включений\(I\).
Використовуйте інформацію про значення,\(f'\) щоб допомогти графіку\(f(x) = x^3 - 6x^2 + 9x + 1\).
Рішення
\(f'(x) = 3x^2 - 12x + 9 = 3(x - 1)(x - 3)\)так\(f'(x) = 0\) тільки коли\(x = 1\) або\(x = 3\). \(f'\)є поліном, тому він завжди визначається.
Єдиними критичними числами для\(f\) є\(x = 1\) і\(x = 3\), і вони ділять дійсну числову лінію на три інтервали:\((-\infty, 1)\)\((1,3)\),, і\((3, \infty)\). На кожному з цих інтервалів функція або завжди збільшується, або завжди зменшується.
Якщо\(x \lt 1\), то\(f '(x) =\) 3 (від'ємне число) (від'ємне число)\(\gt 0\) так\(f\) збільшується.
Якщо\(1 \lt x \lt 3\), то\(f'(x) =\) 3 (додатне число) (від'ємне число)\(\lt 0\) так\(f\) зменшується.
Якщо\(x \gt 3\), то\(f'(x) =\) 3 (додатне число) (додатне число)\(\gt 0\) так\(f\) збільшується.
Незважаючи на те, що ми ще не знаємо значення\(f\) ніде, ми знаємо багато про форму графіка\(f\): коли ми рухаємося зліва направо вздовж\(x\) -осі, графік\(f\) збільшується до тих пір\(x = 1\), поки графік зменшується\(x = 3\), а потім графік збільшується знову. Графік\(f\) робить «повороти», коли\(x = 1\) і\(x = 3\); він має локальний максимум в\(x = 1\), і локальний мінімум на\(x = 3\).

Для побудови графіка\(f\), нам все одно потрібно оцінити\(f\) на кілька значень\(x\), але тільки на дуже мало значень. \(f(1) = 5\), і (1,5) є локальним максимумом\(f\). \(f(3) = 1\), і (3,1) є локальним мінімумом\(f\). Отриманий графік\(f\) показаний тут.

Друга похідна інформація
До цих пір ми використовували лише першу похідну інформацію, але ми також могли б використовувати інформацію з другої похідної, щоб надати більше інформації про форму функції.
- Якщо\(f\) увігнута вгору\((a,b)\), то\(f''(x) \geq 0\) для всіх\(x\) в\((a,b)\).
- Якщо\(f\) увігнутий вниз на\((a,b)\), то\(f''(x) \leq 0\) для всіх\(x\) в\((a,b)\).
Зворотне значення обох з них також вірно:
- Якщо\(f''(x) \geq 0\) для всіх\(x\) в\((a,b),\)\(f\) то увігнутий вгору на\((a,b)\).
- Якщо\(f''(x) \leq 0\) для всіх\(x\) в\((a,b),\)\(f\) то увігнутий вниз на\((a,b)\).
Використовуйте інформацію про значення,\(f''\) щоб допомогти визначити інтервали, на яких функція\(f(x) = x^3 - 6x^2 + 9x + 1\) увігнута вгору і увігнута вниз.
Рішення
Для увігнутості нам знадобиться друга похідна:\( f'(x)=3x^2-12x+9 \), Отже\( f''(x)=6x-12 \).
Щоб знайти можливі точки перегину, встановіть другу похідну рівну нулю. \( 6x-12=0 \), Отже\(x = 2\). Це ділить дійсний числовий рядок на два інтервали:\( (-\infty,2) \) і\( (2,\infty) \).
Бо\(x \lt 2\), друга похідна негативна (наприклад,\( f''(0)=6(0)-12=-12 \)),\(f\) так увігнута вниз. Бо\(x \gt 2\), друга похідна позитивна,\(f\) так увігнута вгору.
Ми могли б включити цю інформацію про увігнутість під час ескізу графіка для попереднього прикладу, і справді ми можемо побачити увігнутість, відображену на показаному графіку.
Використовуйте інформацію про значення\(f'\) і\(f''\) в допомогу графу\( f(x)=x^{2/3} \).
Рішення
\( f'(x)=\frac{2}{3}x^{-1/3} \). Це не визначено в\(x = 0\).
\( f''(x)=-\frac{2}{9}x^{-4/3} \). Це також невизначено в\(x = 0\).
Це створює два інтервали:\(x \lt 0\), і\( x \gt 0\).
На\(x \lt 0\) інтервалі ми могли б перевірити значення, як\(x = -1\):\[ f'(-1)=\frac{2}{3}(-1)^{-1/3}=-\frac{2}{3} \nonumber \] і\[ f''(-1)=-\frac{2}{9}(-1)^{-4/3}=-\frac{2}{9}. \nonumber \]
\( f'(x) \)негативний і\( f''(x) \) негативний, тому можна зробити висновок, що функція зменшується і увігнута вниз на цьому інтервалі.
На\(x \gt 0\) інтервалі ми могли б перевірити значення, як\(x = 1\):\[ f'(1)=\frac{2}{3}(1)^{-1/3}=\frac{2}{3} \nonumber \] і\[ f''(1)=-\frac{2}{9}(1)^{-4/3}=-\frac{2}{9}. \nonumber \]
\( f'(x) \)є позитивним і\( f''(x) \) негативним, тому можна зробити висновок, що функція збільшується і увігнута вниз на цьому проміжку.
Ми також можемо обчислити це\( f(0)=0 \), даючи нам базову точку для графіка. Використовуючи цю інформацію, можна зробити висновок, що графік повинен виглядати наступним чином:

Ескізи без рівняння
Звичайно, графічні калькулятори та комп'ютери чудово справляються з графічними функціями. Обчислення забезпечує спосіб висвітлити те, що може бути прихованим або поза увагою, коли ми графуємо за допомогою технології. Що ще важливіше, обчислення дає нам можливість подивитися на похідні функцій, для яких не дано рівняння. Ми вже бачили ідею цього ще в розділі 2.3, де ми накидали похідну від двох графіків, оцінюючи нахили на кривих.
Ми можемо узагальнити всю похідну інформацію про форму в таблиці.
| \( f(x) \) | Збільшення | Зниження | Увігнуті вгору | увігнуті вниз |
| \( f'(x) \) | \( + \) | \( - \) | Збільшення | Зниження |
| \( f''(x) \) | \( + \) | \( - \) |
Коли\(f'(x) = 0\), графік\(f\) може мати локальний max або min.
Коли\(f''(x) = 0\), графік\(f\) може мати точку перегину.
Банківський баланс компанії\(B\), в мільйоні доларів, через\(t\) кілька тижнів після випуску нового продукту показаний на графіку нижче. Намалюйте графік граничного балансу — курсу, за яким баланс банку змінювався з плином часу.

Рішення
Зверніть увагу, що оскільки дотична лінія буде горизонтальною приблизно\(t = 0.6\) і\(t = 3.2\), похідна буде дорівнює 0 в цих точках.
Потім ми можемо визначити інтервали, на яких вихідна функція збільшується або зменшується. Це скаже нам, коли похідна функція позитивна або негативна.
| Інтервал | \( B(t) \) | \( B'(t) \) |
| \(0 \lt t \lt 0.6\) | Зниження | Негативний |
| \( 0.6 \lt t \lt 3.2 \) | Збільшення | Позитивні |
| \( t \gt 3.2 \) | Зниження | Негативний |
Здається, є точки перегину приблизно\(t =1.5\) і\(t = 5.5\). У цих точках похідна буде змінюватися від збільшення до зменшення або навпаки, тому похідна матиме локальний max або min у цих точках.
Дивлячись на проміжки увігнутості:
| Інтервал | \( B(t) \) | \( B'(t) \) |
| \( 0 \lt t \lt 1.5 \) | Увігнуті вгору | Збільшення |
| \( 1.5 \lt t \lt 5.5 \) | увігнуті вниз | Зниження |
| \( t \gt 5.5 \) | Увігнуті вгору | Збільшення |
Якби ми хотіли отримати більш точний ескіз похідної функції, ми могли б також оцінити похідну в декількох точках:
| \( t \) | \( B'(t) \) |
| 0 | -10 |
| 1.5 | 3 |
| 6 | -1 |
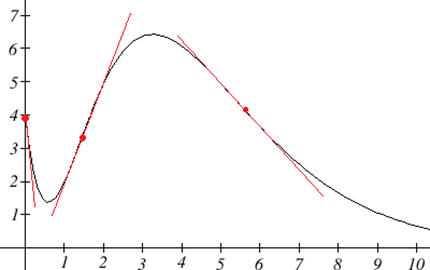
Тепер ми можемо накидати похідну. Ми знаємо кілька значень похідної функції, і на кожному інтервалі ми знаємо потрібну нам форму. Ми можемо використовувати це, щоб створити приблизне уявлення про те, як повинен виглядати графік.
Згладжування цього дає нам хорошу оцінку для графіка похідної.