3.5: Ескіз кривої

Last updated
Save as PDF

Page ID: 60702

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Ми дізналися, як ми можемо зрозуміти поведінку функції на основі її першої та другої похідних. Поки ми розглядали властивості функції окремо (збільшення і зменшення, увігнуті вгору і увігнуті вниз і т.д.), ми об'єднуємо їх тут, щоб отримати точний графік функції без побудови безлічі сторонніх точок.

Навіщо морочитися? Графічні утиліти дуже доступні, будь то на комп'ютері, ручному калькуляторі або смартфоні. Ці ресурси, як правило, дуже швидкі і точні. Ми побачимо, що наш метод не особливо швидкий — він зажадає часу (але це не складно). Отже, ще раз: навіщо турбувати?

Ми намагаємося зрозуміти поведінку функції на$f$ основі інформації, наданої її похідними. Хоча всі похідні функції передають інформацію про неї, виявляється, що «більшість» поведінки, про яку ми дбаємо, пояснюється$f'$ і$f''$. Розуміння взаємодій між графіком$f$$f'$ і і$f'$ важливо. Щоб отримати це розуміння, можна стверджувати, що все, що потрібно, - це подивитися на безліч графіків. Це вірно до певної точки, але дещо схоже на те, що людина розуміє, як працює двигун, подивившись лише на фотографії. Це правда, що основні ідеї будуть передані, але «практичний» доступ підвищує розуміння.

Наступна ключова ідея узагальнює те, що ми дізналися до цього часу, що застосовується до ескізів графіків функцій і дає основу для об'єднання цієї інформації. Далі йде кілька прикладів.

Ключова ідея 4: Ескіз кривої

Щоб зробити точний ескіз заданої функції$f$, розглянемо наступні кроки.

Знайдіть домен домену$f$. Як правило, ми припускаємо, що домен - це весь реальний рядок, а потім знайти обмеження, наприклад, де знаменник дорівнює 0 або де негативи з'являються під радикалом.
Знайдіть критичні значення$f$.
Знайдіть можливі точки перегину$f$.
Знайдіть розташування будь-яких вертикальних асимптотів$f$ (зазвичай це робиться у поєднанні з пунктом 1 вище).
Розглянемо межі$\displaystyle \lim_{x\to-\infty}f(x)$ і$\displaystyle \lim_{x\to\infty}f(x)$ визначте кінцеву поведінку функції.
Створіть числову лінію, яка включає всі критичні точки, можливі точки перегину та місця вертикальних асимптотів. Для кожного створеного інтервалу визначте, збільшується чи$f$ зменшується, увігнута вгору або вниз.
Оцініть$f$ в кожній критичній точці і можливій точці перегину. Розкладіть ці точки на набір осей. З'єднайте ці точки кривими, що проявляють належну увігнутість. Ескіз асимптотів і$x$ і$y$ перехоплює там, де це можливо.

Приклад$\PageIndex{1}$: curve sketching

Використовуйте Key Idea 4 для ескізу$f(x) = 3x^3-10x^2+7x+5$.

Рішення

Домен$f$ - це вся реальна лінія; немає значень,$x$ для яких$f(x)$ не визначено.
Знайдіть критичні значення$f$. Обчислюємо$f'(x) = 9x^2-20x+7$. Використовуйте квадратичну формулу, щоб знайти коріння$f'$:
$x =\ frac {20\ pm\ sqrt {(-20) ^2-4 (9)}} {2 (9)}} =\ frac19\ left (10\ pm\ sqrt {37}\ праворуч)\ Rightarrow x\ приблизно 0.435, 1.787. $$
Знайдіть можливі точки перегину$f$. Обчислити$f''(x) = 18x-20$. У нас є
$ f'p (x) = 0\ Стрілка вправо х = 10/9\ приблизно 1.111. $$
Вертикальних асимптотів немає.
Визначено кінцеву поведінку, використовуючи межі$x$ наближення до$\pm$ нескінченності. $\ lim_ {x\ to -\ infty} f (x) = -\ infty\ qquad\ lim_ {x\ to\ infty} f (x) =\ intty. $$У нас немає горизонтальних асимптотів.
Розміщуємо значення$x=(10\pm\sqrt{37})/9$ і$x=10/9$ на числовому рядку, як показано на малюнку$\PageIndex{1}$. Ми відзначаємо кожен підінтервал як зростаючий або зменшується, увігнутий вгору або вниз, використовуючи методи, використовувані в розділах 3.3 і 3.4.

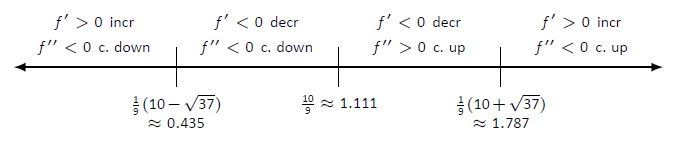
$imageedit_1_8640707384.png$

Малюнок$\PageIndex{1}$: Числовий рядок для$f$ у прикладі$\PageIndex{1}$.

Відкладаємо відповідні точки на осях, як показано на малюнку,$\PageIndex{2a}$ і з'єднуємо точки прямими лініями. На малюнку$\PageIndex{2b}$ ми коригуємо ці лінії, щоб продемонструвати належну увігнутість. Наша крива перетинає$y$ вісь на$y=5$ і перетинає$x$ вісь поблизу$x=-0.424$. На малюнку$\PageIndex{2c}$ ми показуємо графік$f$ намальованого за допомогою комп'ютерної програми, перевіряючи точність нашого ескізу.

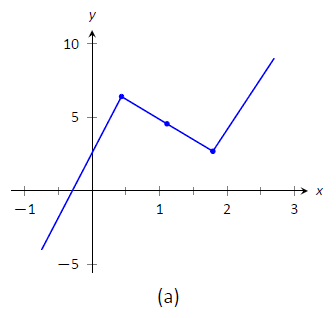
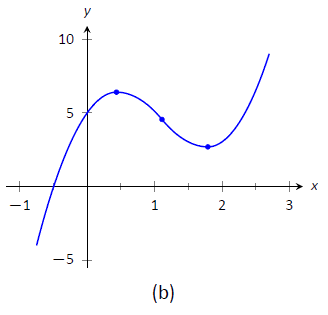
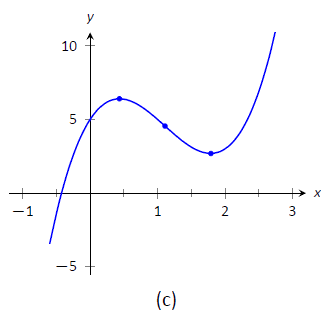
$imageedit_4_5597745392.png$ $imageedit_7_4757736358.png$ $imageedit_10_8560889020.png$

Малюнок$\PageIndex{2}$: Начерки$f$ на прикладі$\PageIndex{1}$.

Приклад$\PageIndex{2}$: Curve sketching

Ескіз$f(x) = \dfrac{x^2-x-2}{x^2-x-6}$.

Рішення

Ми знову слідуємо крокам, описаним у Key Idea 4.

При визначенні домену ми припускаємо, що це все дійсні цифри і шукаємо обмеження. Знаходимо, що при$x=-2$ і$x=3$,$f(x)$ не визначено. Таким чином, домен$f$ є$D = \{\text{real numbers } x\ | \ x\neq -2,3\}$.
Щоб знайти критичні значення$f$, спочатку знаходимо$f'(x)$. Використовуючи часткове правило, ми знаходимо $f' (x) =\ frac {-8x+4} {(x^2+x-6) ^2} =\ frac {-8x+4} {(x-3) ^2 (x+2) ^2}. $$f'(x) = 0$ коли$x = 1/2$, і$f'$ не визначено, коли$x=-2,3$. Оскільки$f'$ не визначено лише тоді, коли$f$ є, це не критичні значення. Єдине критичне значення - це$x=1/2$.
Щоб знайти можливі точки перегину, знайдемо$f''(x)$, знову застосовуючи правило частки: $$f "(x) =\ frac {24x^2-24x+56} {(x-3) ^3 (x+2) ^3}. $$Ми знаходимо, що ніколи не$f''(x)$ дорівнює 0 (встановлюючи чисельник рівний 0 і вирішуючи для$x$, ми знаходимо єдине коріння цієї квадратики уявні) і$f'$ не визначено коли$x=-2,3$. Таким чином, увігнутість, можливо, зміниться лише при$x=-2$ і$x=3$.
Вертикальні асимптоти$f$ знаходяться в$x=-2$ і$x=3$, місця, де$f$ не визначено.
Виникає горизонтальна асимптота$y=1$, як$\lim_{x\to -\infty}f(x) = 1$ і$\lim_{x\to\infty}f(x) =1$.
Розміщуємо значення$x=1/2$,$x=-2$ і$x=3$ на числовому рядку, як показано на малюнку$\PageIndex{3}$. Ми відзначаємо в кожному інтервалі, збільшується чи$f$ зменшується, увігнута вгору або вниз. Ми бачимо, що$f$ має відносний максимум при$x=1/2$; увігнутість змінюється лише на вертикальних асимптотах.

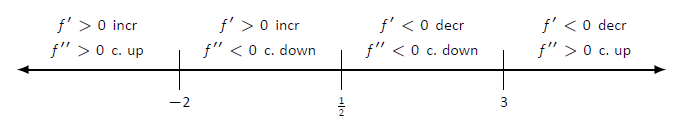
$imageedit_19_9171189926.png$

Рисунок$\PageIndex{3}$: Числовий рядок для$f$ у прикладі$\PageIndex{2}$

На малюнку$\PageIndex{4a}$ ми відкладаємо точки від числової лінії на набір осей і з'єднуємо точки прямими лініями, щоб отримати загальне уявлення про те, як виглядає функція (ці лінії ефективно лише передають інформацію про збільшення/зменшення). На$\PageIndex{4b}$ малюнку коригуємо графік з відповідною увігнутістю. Ми також показуємо$f$ перетин$x$$x=-1$ осі в і$x=2$.

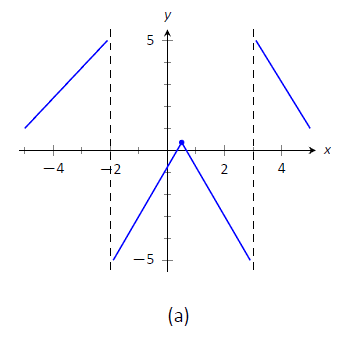
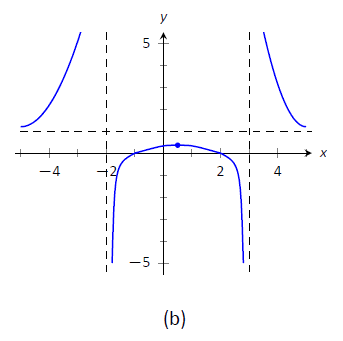
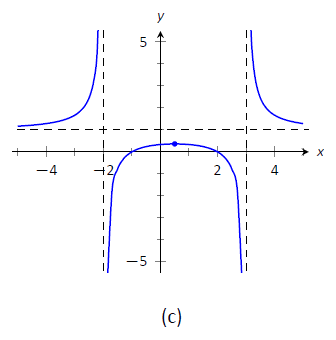
$imageedit_19_5351375926.png$ $imageedit_19_3017526857.png$ $imageedit_40_5672980539.png$

Малюнок$\PageIndex{4}$: Начерки$f$ на прикладі$\PageIndex{2}$.

$\PageIndex{4c}$На малюнку зображений згенерований комп'ютером графік$f$, який перевіряє точність нашого ескізу.

Приклад$\PageIndex{3}$: Curve sketching

ескіз$f(x) = \frac{5(x-2)(x+1)}{x^2+2x+4}.$

Рішення

Ми знову слідуємо за Ключовою Ідеєю 4

Припускаємо, що домен всіх$f$ дійсних чисел і розглянемо обмеження. Єдині обмеження настають, коли знаменник дорівнює 0, але цього ніколи не відбувається. Тому домен всіх$f$ дійсних чисел,$\mathbb{R}$.
Знаходимо критичні значення,$f$ встановивши$f'(x)=0$ і вирішивши для$x$. Знаходимо
$f' (x) =\ frac {15x (x+4)} {(x^2+2x+4) ^2}\ quad\ Стрілка вправо\ quad f' (x) = 0\ текст {коли}\ x = -4,0. $$
Знаходимо можливі точки перегину, вирішивши$f''(x) = 0$ для$x$. Ми знаходимо
$f'p (x) = -\ frac {30x^3+180x^2-240} {(x^2+2x+4) ^3} .$$ Кубічна в чисельнику не дуже «красиво». Натомість ми наближаємо коріння в$x= -5.759$,$x=-1.305$ і$x=1.064$.
Вертикальних асимптотів немає.
У нас є горизонтальна асимптота$y=5$, як$\lim_{x\to-\infty}f(x) = \lim_{x\to\infty}f(x) = 5$.
Ми розміщуємо критичні точки та можливі точки на числовій лінії, як показано на малюнку,$\PageIndex{5}$ і відзначаємо кожен інтервал як зростаючий/зменшений, увігнутий вгору/вниз відповідним чином.

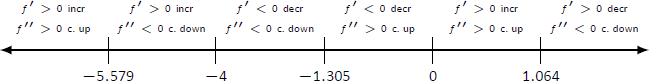
$imageedit_28_4539688605.png$

Малюнок$\PageIndex{5}$: Числовий рядок для$f$ у прикладі$\PageIndex{3}$.

На малюнку$\PageIndex{6a}$ ми будуємо значні точки від числової лінії, а також два$x=-1$ корені і$f$$x=2$, і з'єднуємо точки прямими лініями, щоб отримати загальне враження про графік. На$\PageIndex{6b}$ малюнку додаємо увігнутість. $\PageIndex{6c}$На малюнку зображений згенерований комп'ютером графік$f$, що підтверджує наші результати.

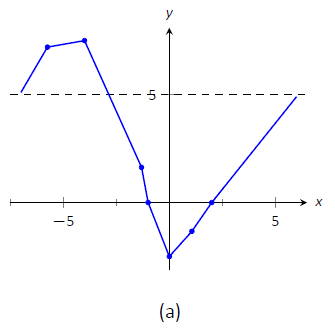
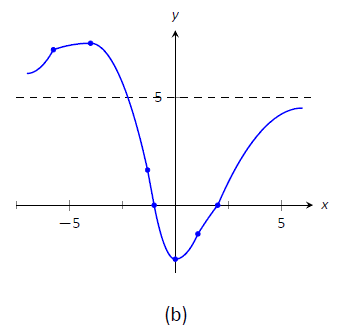
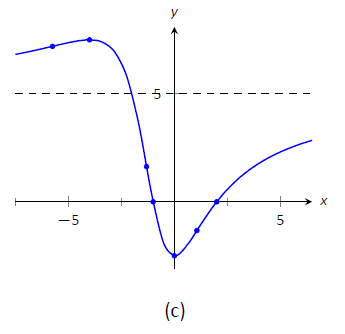
$imageedit_31_2310568347.png$ $imageedit_34_3394066978.png$ $imageedit_37_6901347726.png$

Малюнок$\PageIndex{6}$: Начерки$f$ на прикладі$\PageIndex{3}$.

У кожному з наших прикладів ми знайшли кілька значущих моментів на графіку,$f$ які відповідали змінам збільшення/зменшення або увігнутості. Ми з'єднали ці точки прямими лініями, потім скориговані на увігнутість, і закінчили показуючи дуже точний, генерується комп'ютером графік.

Чому комп'ютерна графіка така хороша? Це не тому, що комп'ютери «розумніші», ніж ми. Швидше, це багато в чому тому, що комп'ютери набагато швидше обчислюються, ніж ми. Загалом, графіки комп'ютерів функціонують так само, як і більшість учнів, коли спочатку навчаються малювати графіки: вони будують однаково розташовані точки, потім з'єднують точки за допомогою ліній. Використовуючи багато точок, сполучні лінії короткі, а графік виглядає гладким.

Це робить прекрасну роботу з графіків у більшості випадків (насправді, це метод, який використовується для багатьох графіків у цьому тексті). Однак у регіонах, де графік дуже «кривий», це може генерувати помітні гострі краї на графіку, якщо не використовується велика кількість точок. Високоякісні системи комп'ютерної алгебри, такі як Mathematica, використовують спеціальні алгоритми для побудови безлічі точок лише там, де графік є «кривим».

На малюнку наведено$y=\sin x$ графік$\PageIndex{7}$, згенерований Mathematica. Маленькі точки представляють кожне з місць, де Mathematica вибірки функції. Зверніть увагу$\sin x$, як на «поворотах» використовується багато точок; де$\sin x$ відносно прямий, використовується менше точок. (Багато точок також використовуються в кінцевих точках, щоб забезпечити точність «кінцевої поведінки».)

$альт$

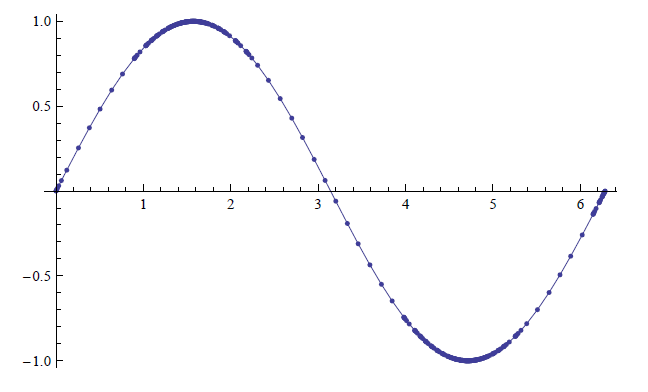
Малюнок$\PageIndex{7}$: Графік$y=\sin x$ згенерованого компанією Mathematica.

Звідки Mathematica знає, де граф «пишний»? Обчислення. Коли ми вивчаємо кривизну в наступному розділі, ми побачимо, як перша та друга похідні функції працюють разом, щоб забезпечити вимірювання «кривизни». Mathematica використовує алгоритми для визначення областей «високої кривизни"' і відображає там додаткові точки.

Знову ж таки, метою цього розділу є не «Як графік функції, коли немає комп'ютера, який би допоміг». Швидше за все, мета полягає в тому, що «Зрозумійте, що форма графіка функції багато в чому визначається розумінням поведінки функції в декількох ключових місцях». У прикладі$\PageIndex{3}$ ми змогли точно намалювати складний графік, використовуючи лише 5 балів і знання асимптотів!

Є багато застосувань нашого розуміння похідних за межами кривих ескізів. Наступний розділ досліджує деякі з цих додатків, демонструючи лише кілька видів проблем, які можна вирішити за допомогою базових знань про диференціацію.