2.10: Прикладна оптимізація
- Page ID
- 60358
Ми використовували похідні, щоб допомогти знайти максимуми та мінімуми деяких функцій, заданих рівняннями, але дуже малоймовірно, що хтось просто передасть вам функцію і попросить вас знайти її крайні значення. Як правило, хтось опише проблему і попросить вашої допомоги у максимізації або мінімізації чогось: Який найбільший пакет обсягу, який прийме поштове відділення?
; Який найшвидший спосіб дістатися звідси туди?
; або Який найменш витратний спосіб виконати якесь завдання?
У цьому розділі ми обговоримо, як знайти ці екстремальні значення за допомогою обчислення.
Макс/хв додатків
Менеджер садового магазину хоче побудувати прямокутний корпус площею 600 квадратних футів на стоянці магазину, щоб відобразити деяке обладнання. Три сторони вольєра будуть побудовані з паркану з червоного дерева, вартістю 7 доларів за ходову ногу. Четверта сторона буде побудована з цементних блоків, вартістю $14 за погонну ногу. Знайдіть розміри найменш витратного такого вольєра.
Процес знаходження максимумів або мінімумів називається оптимізацією. Функція, яку ми оптимізуємо, називається об'єктивною функцією (або об'єктивним рівнянням). Об'єктивну функцію можна розпізнати за її близькістю до est
слів (найбільший, найменший, найвищий, найдальший, самий,...). Подивіться на приклад садового магазину; функція витрат є об'єктивною функцією.
У багатьох випадках в задачі є дві (або більше) змінних. У прикладі садового магазину знову ж таки, довжина і ширина вольєра невідомі. Якщо є рівняння, яке пов'язує змінні, ми можемо вирішити для однієї з них з точки зору інших, і записати об'єктивну функцію як функцію лише однієї змінної. Рівняння, що пов'язують змінні таким чином, називаються рівняннями обмежень. Рівняння обмежень завжди є рівняннями, тому вони матимуть знаки рівності. Для садового магазину фіксована площа стосується довжини і ширини вольєра. Це дасть нам наше рівняння обмеження.
- Перекладіть англійську постановку задачі рядок за рядком у картинку (якщо це стосується) та в математику. Це часто найважчий крок!
- Визначте об'єктивну функцію. Шукайте слова, що позначають найбільше або найменше значення.
- Якщо у вас, здається, є дві або більше змінних, знайдіть рівняння обмеження. Подумайте про англійське значення слова
constraint
і пам'ятайте, що рівняння обмеження матиме знак дорівнює. - Вирішити рівняння обмеження для однієї змінної і підставити в цільову функцію. Тепер у вас є рівняння однієї змінної.
- Якщо у вас, здається, є дві або більше змінних, знайдіть рівняння обмеження. Подумайте про англійське значення слова
- Використовуйте обчислення, щоб знайти оптимальні значення. (Візьміть похідну, знайдіть критичні точки, тестуйте. Не забудьте перевірити кінцеві точки!)
- Озирніться назад на питання, щоб переконатися, що ви відповіли на запитання. Перекладіть свою відповідь на номер на англійську мову.
Ось посилання на приклади, використані у відео в цьому розділі: Приклади прикладної оптимізації.
Менеджер садового магазину хоче побудувати прямокутний корпус площею 600 квадратних футів на стоянці магазину, щоб відобразити деяке обладнання. Три сторони вольєра будуть побудовані з паркану з червоного дерева, вартістю 7 доларів за ходову ногу. Четверта сторона буде побудована з цементних блоків, вартістю $14 за погонну ногу. Знайдіть розміри найменш витратного такого вольєра.
Спочатку перекладіть рядок за рядком в математику і картинку:
| Текст | Переклад |
|
Менеджер садового магазину хоче побудувати прямокутний корпус площею 600 квадратних футів на стоянці магазину, щоб відобразити деяке обладнання. Три сторони вольєра будуть побудовані з паркану з червоного дерева, вартістю 7 доларів за ходову ногу. Четверта сторона буде побудована з цементних блоків, вартістю $14 за погонну ногу. Знайдіть розміри найменш витратного такого вольєра. |
Нехай\(x\) і\(y\) будуть розміри вольєра, при\(y\) цьому довжина сторони, виготовленої з блоків. Потім:\[\text{Area} = A = xy = 600.\nonumber \] \(2x + y\)коштує 7 доларів за фут,\(y\) коштує 14 доларів за фут, тому\[\text{Cost} = C = 7(2x + y) + 14y = 14x + 21y.\nonumber \] Знайти\(x\) і\(y\) так, щоб\(C\) зведено до мінімуму. |
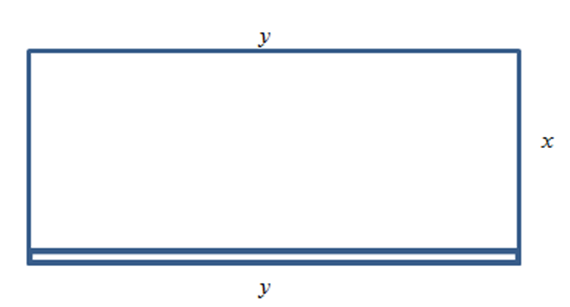
Об'єктивною функцією є функція витрат, і ми хочемо її мінімізувати. Як він стоїть, хоча, він має дві змінні, тому нам потрібно використовувати рівняння обмеження. Рівняння обмеження - це фіксована площа\(A = xy = 600\). \(A\)Вирішіть,\(x\) щоб отримати\( x=\frac{600}{y} \), а потім підставити в\(C\):\[C=14\left(\frac{600}{y}\right)+21y=\frac{8400}{y}+21y.\nonumber \]
Тепер у нас є функція тільки одна змінна, так що ми можемо знайти мінімум за допомогою обчислення.
\[C'=-\frac{8400}{y^2}+21\nonumber \]\(C'\)не визначено для\(y = 0\), і\(C' = 0\) коли\(y = 20\) або\(y = -20\).
З цих трьох критичних чисел, тільки має\(y = 20\) сенс (знаходиться в області фактичної функції) - пам'ятайте, що\(y\) це довжина, тому вона не може бути негативною, і\(y = 0\) означатиме, що немає корпусу взагалі, тому він не міг мати площу 600 квадратних футів.
Test\(y = 20\) (тут ми вибрали другий похідний тест):\[C''=\frac{16800}{y^3} \gt 0,\nonumber \] так що це локальний мінімум.
Оскільки це єдина критична точка в області, це повинен бути глобальний мінімум. Повертаючись до нашої функції обмеження, ми можемо знайти, що коли\(y = 20\),\(x = 30\). Розміри корпусу, що мінімізують вартість, становлять 20 футів на 30 футів.
Намагаючись максимізувати свої доходи, підприємства також стикаються з обмеженням споживчого попиту. Хоча бізнес хотів би бачити багато продуктів за дуже високою ціною, як правило, попит зменшується з ростом ціни на товари. У простих випадках ми можемо побудувати цю криву попиту, щоб дозволити нам максимізувати дохід.
Промоутер концерту виявив, що якщо вона продає квитки по 50 доларів кожен, вона може продати 1200 квитків, але за кожні 5 доларів вона піднімає ціну, на 50 менше людей відвідує. За якою ціною вона повинна продавати квитки, щоб максимізувати свій дохід?
Ми намагаємося максимізувати дохід, і знаємо\( R=pq \), що, де\(p\) ціна за квиток, і\(q\) це кількість проданих квитків.
Проблема дає інформацію про взаємозв'язок попиту між ціною та кількістю — у міру зростання ціни попит зменшується. Нам потрібно знайти формулу для цього взаємозв'язку. Щоб дослідити, давайте порахуємо, що буде з відвідуваністю, якщо ми підвищимо ціну:
| Ціна,\( p \) | 50 | 55 | 60 | 65 |
| Кількість,\( q \) | 1200 | 1150 | 1100 | 1050 |
Ви можете розпізнати це як лінійний зв'язок. Ми можемо знайти нахил для відносин, використовуючи дві точки:\[m=\frac{1150-1200}{55-50}=\frac{-50}{5}=-10.\nonumber \]
Ви можете помітити, що другий крок у цьому розрахунку безпосередньо відповідає постановці проблеми: відвідуваність падає на 50 осіб за кожні 5 доларів, коли ціна зростає.
Використовуючи точку-нахил форми лінії, ми можемо записати рівняння, що стосується ціни та кількості:\[q-1200=-10(p-50).\nonumber \]
Спрощення до ухилу перехоплення форми дає рівняння попиту\[ q=1700-10p. \nonumber \]
Підставивши це в наше рівняння доходу, ми отримуємо рівняння доходу, що включає лише одну змінну:\[R=pq=p(1700-10p)=1700p-10p^2.\nonumber \]
Тепер ми можемо знайти максимум цієї функції, знайшовши критичні числа. \( R'=1700-20p \), Отже,\( R'=0 \) коли\(p = 85\).
Використовуючи другу похідну тест,\( R''=-20 \lt 0 \) (для будь-якого значення\( p \)), тому критичне число є локальним максимумом. Оскільки це єдине критичне число, можна також зробити висновок, що це глобальний максимум.
Промоутер зможе максимізувати дохід, стягуючи $85 за квиток. За цією ціною вона буде продавати\( q=1700-10(85)=850 \) квитки, приносячи дохід у розмірі 72 250 доларів.
Маржинальний дохід = гранична вартість
Можливо, ви чули раніше, що прибуток максимізується, коли граничні витрати та граничний дохід рівні.
Тепер ви можете зрозуміти, чому люди так говорять! (Хоча це не зовсім так.)
Припустимо, ми хочемо максимізувати прибуток.
Тепер ми знаємо, що робити — знайти функцію прибутку, знайти її критичні точки, протестувати їх і т.д.
Але пам'ятайте, що Прибуток = Виручка - Вартість. Так що прибутк' = Виручка' - Вартість'. Тобто похідною від функції прибутку є\(MR - MC\).
Тепер знайдемо критичні точки — вони будуть де Profit' = 0 або не визначено. Прибуток' = 0 коли\(MR - MC = 0\), або де\(MR = MC\).
Прибуток має критичні моменти, коли граничний дохід і гранична вартість рівні.
У всіх випадках, які ми побачимо в цьому класі, Прибуток буде дуже добре себе вести, і нам не доведеться турбуватися про пошук критичних точок, де прибуток не визначено. Але пам'ятайте, що не всі критичні точки локальні макс! Місця, де\(MR = MC\) може представляти локальний max, місцевий min, або жоден.
Компанія продає\(q\) стрічкові намотувачі на рік за кожну\(\$p\) намотувальну стрічку. Функція попиту для намотувачів стрічки задається:\(p=300-0.02q\). Стрічкові намотувачі коштують 30 доларів за штуку на виготовлення, плюс є постійні витрати в розмірі 9000 доларів на рік. Знайдіть величину, де прибуток максимізується.
Ми хочемо максимізувати прибуток, але формули прибутку не дано. Отже, давайте зробимо один. Ми можемо знайти функцію для Revenue =\(pq\) за допомогою функції попиту для\(p\). \[R(q)=(300-0.02q)q=300q-0.02q^2.\nonumber \]
Ми також можемо знайти функцію для Cost, використовуючи змінну вартість $30 за моталку стрічки, плюс фіксовану вартість:\[C(q)=9000+30q.\nonumber \]
Склавши їх воєдино, отримуємо функцію для Profit:\[P(q)=R(q)-C(q)=\left(300q-0.02q^2\right)-(9000+30q)=-0.02q^2+270q-9000\nonumber \]
Тепер у нас є два варіанти. Ми можемо знайти критичні точки прибутку, взявши похідну\(P(q)\) безпосередньо, або ми можемо знайти\(MR\)\(MC\) і встановити їх рівними. (Природно, ми отримаємо однакову відповідь в будь-якому випадку.)
Давайте скористаємося\(MR = MC\) цим часом. \[ \begin{align*} MR & = 300-0.04q\\ MC & = 30\\ 300-0.04q & = 30\\ 270 & = 0.04q\\ q & = 6750 \end{align*} \nonumber \]
Єдина критична точка - на\(q = 6750\). Тепер ми повинні бути впевнені, що це локальний макс, а не локальний хв. У цьому випадку ми розглянемо графік\(P(q)\) - це парабола, що відкривається вниз, так що це повинно бути локальним максимумом. І оскільки це єдина критична точка, вона також повинна бути глобальним максимумом.
Прибуток максимізується, коли продають 6750 стрічкових намотувачів.
Середня вартість = гранична вартість
Середня вартість мінімізується, коли середня вартість = гранична вартість
- це ще одна приказка, яка не зовсім вірна; в цьому випадку правильним твердженням є:
Середня вартість має критичні точки, коли середня вартість і гранична вартість рівні.
Давайте подивимося на геометричний аргумент тут. Пам'ятайте, що середня вартість - це нахил діагональної лінії, лінії від початку до точки на кривій загальної вартості. Якщо ви перемістіть чітку пластикову лінійку навколо, ви побачите (і відчуєте), що нахил діагональної лінії найменший, коли діагональна лінія просто торкається кривої вартості - коли діагональна лінія насправді є дотичною лінією - коли середня вартість дорівнює граничній вартості.
Вартість в доларах на виготовлення\(q\) подарункових кошиків дається по\(C(q) = 160+2q+ .1q^2\). Знайдіть кількість, де середня вартість мінімальна.
Рішення
\(A(q) = \frac{C(q)}{q} = \frac{160}{q} + 2 + .1q\). Ми могли б знайти критичні точки\(A'\), знайшовши або встановивши середню вартість на граничну вартість; ми зробимо останнє цього разу.
\[MC(q) = 2+ .2q. \nonumber\]
Отже, ми хочемо вирішити:
\[\begin{align*} \frac{160}{q} +2+.1q &= 2+.2q \\ \frac{160}{q} &= .1q \\ 1600 &= q^2 \\ q&=40 \end{align*}\]
Критичною точкою середньої вартості є коли\(q = 40\).
Зверніть увагу, що нам ще належить підтвердити, що критична точка мінімальна. Для цього ми можемо використовувати перший або другий похідний тест на\(A(q)\).
\[\begin{align*} A'(q) = \frac{-160}{q^2} +.1 \\ A''(q) = \frac{320}{q^3} >0 \end{align*}\]
Друга похідна є позитивною для всіх позитивних\(q\), так що це означає, що це локальний min. Середня вартість мінімізується при виготовленні 40 подарункових кошиків; при такій кількості середня вартість становить 10 доларів за кошик.
