2.11: Інші програми
- Page ID
- 60335
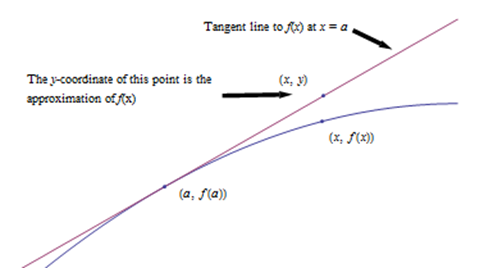
Наближення дотичної лінії
Коли ми вперше подумали про похідну, ми використовували нахил січних ліній через крихітні інтервали, щоб наблизити похідну:
\[f'(a) \cong \frac{\Delta y}{\Delta x} = \frac{f(x) - f(a)}{x-a} \nonumber\]
Тепер, коли у нас є інші способи пошуку похідних, ми можемо використовувати це наближення, щоб піти іншим шляхом. Вирішіть вираз вище для\(f(x)\), і ви отримаєте наближення дотичної лінії:
Щоб наблизити значення\(f(x)\) використання TLA, знайдіть деякі\(a\) де
- \(a\)і\(x\) є «близькими», і
- Ви знаєте точні значення обох\(f (a)\) і\(f ‘(a)\). Тоді\[f(x) \cong f(a) + f'(a)(x-a).\nonumber\]
Ще один спосіб подивитися на цю ж формулу:
\[\Delta y \cong f'(a) \Delta x\nonumber\]
Наскільки близько близько? Це залежить від форми графіка\(f\). Загалом, чим ближче, тим краще.
Припустимо, ми знаємо, що\(g(20) = 5\) і\(g’(20) = 1.4\). Використовуйте цю інформацію для наближення\(g(23)\) і\(g(18)\).
Рішення
Використання наближення дотичної прямої:
\(g(23) \approx 5 + (1.4)(23 – 20) = 9.2\)
\(g(18) \approx 5 + (1.4)(18 – 20) = 2.2\)
Зауважте, що ми не знаємо, чи близькі ці наближення, але вони найкраще, що ми можемо зробити з обмеженою інформацією, з якої ми маємо почати. Зверніть увагу також, що 18 і 23 начебто близькі до 20, тому ми можемо сподіватися, що ці наближення досить хороші. Ми відчували б себе більш впевнено, використовуючи цю інформацію для наближення\(g(20.003)\). Ми відчували б себе дуже невпевненими, використовуючи цю інформацію для наближення\(g(55)\).
Еластичність
Ми знаємо, що функції попиту зменшуються, тому, коли ціна зростає, затребувана кількість знижується. Але як щодо доходу =\( \times \) кількість ціни? Коли зросте ціна, дохід знизиться, тому що попит так сильно впав? Або дохід збільшиться, тому що попит не дуже впав?
Припустимо, функція попиту компанії є\(D(p) = 100 - p^2\), а поточна ціна компанії становить 5 доларів. Що буде з доходом, якщо вони підвищать ціну на $0,05?
Рішення
Нас більше цікавить, як зміна ціни порівнюється зі зміною попиту, тому ми збираємось конвертувати все на відносні (відсоткові) зміни.
Ціна зросла на\[\frac{\Delta p}{p} = \frac{\$0.05}{\$5} = 0.01 = 1\%\nonumber \]
Попит зменшився з\(D(5) = 100-5^2 = 75\) до\(D(5.05) = 100-5.05^2 = 74.4975\), загальна зміна\(75-74.4975 = -0.5025\). Як відносна зміна, це\[\frac{\Delta q}{q} = \frac{-0.05025}{75} = -0.0067 = -0.67\%\nonumber \]
Підвищивши ціну на 1%, попит впав лише на 0,67%. Оскільки ціна зростає більше, ніж падає попит, ми очікуємо, що загальний дохід збільшиться. У цьому випадку ми говоримо, що попит нееластичний.
Еластичність попиту - це показник того, як попит реагує на зміну цін. Це нормалізується - це означає, що конкретні ціни та кількості не мають значення, і все розглядається як зміна відсотків.
Слідуючи логіці наведеного вище прикладу, ми хочемо порівняти відносну зміну попиту з відносною зміною ціни, або іншими словами, ми хочемо подивитися на\[\frac{\frac{\Delta q}{q}}{\frac{\Delta p}{p}}.\nonumber \] Апроксимуючи зміни попиту та ціни похідними, ця формула спрощує\[\frac{\frac{dq}{q}}{\frac{dp}{p}} = \frac{p}{q}\cdot\frac{dq}{dp}\nonumber \]
Враховуючи функцію попиту, яка надає\(q\) in terms of \(p\), so \(q = D(p)\), the еластичність попиту, є\[E=\left|\frac{p}{q}\cdot \frac{dq}{dp}\right| = \left|\frac{p}{q}\cdot D'(p)\right| \nonumber \]
(Зверніть увагу, що оскільки попит є спадною функцією\(p\), похідна є негативною. Тому ми маємо абсолютні значення — так завжди\(E\) будуть позитивними.)
Ви також можете побачити цю формулу,\[E = - \frac{p \cdot D'(p)}{D(p)}\nonumber \] записану як Дві форми рівняння еквівалентні, і ви можете використовувати будь-яку.
- Якщо\(E \lt 1\), ми говоримо, що попит нееластичний. При цьому підвищення цін збільшує виручку.
- Якщо\(E \gt 1\), ми говоримо, що попит еластичний. При цьому підвищення цін знижує виручку.
- Якщо\(E = 1\), скажемо, попит унітарний. \(E = 1\)в критичних точках дохідної функції.
Якщо ціна підвищиться на 1%, попит зменшиться на Е%.
Компанія продає\( q \) стрічкові намотувачі на рік\( p \) за $ за намотування стрічки. Функція попиту для стрічкових намотувачів задається\( p=300-0.02q \). Знайти еластичність попиту, коли ціна становить 70 доларів за штуку. Чи призведе підвищення ціни до збільшення виручки?
Рішення
По-перше, нам потрібно вирішити рівняння\( q \) попиту, щоб воно давало з точки зору\( p \), так що ми можемо знайти\( \frac{dq}{dp} \):\( p=300-0.02q \), так\( q=15000-50p \). Потім\( \frac{dq}{dp}=-50 \).
Нам потрібно знайти,\( q \) коли\( p = 70 \):\[ q = 11500. \nonumber \]
Тепер обчислюйте\[ E=\left| \frac{p}{q}\cdot\frac{dq}{dp} \right|=\left| \frac{70}{11500}\cdot(-50) \right| \approx 0.3 \nonumber \]
\(E \lt 1\), тому попит нееластичний. Збільшення ціни на 1% призведе лише до падіння попиту на 0,3%. Збільшення ціни призвело б до збільшення виручки, тому здається, що компанія повинна збільшити свою ціну.
Попит на продукти, які люди повинні купувати, такі як цибуля, як правило, нееластичний. Навіть якщо ціна піде вгору, людям все одно доведеться купувати приблизно таку ж кількість цибулі, і виручка не піде вниз. Попит на товари, без яких люди можуть обійтися, або відкласти покупку, наприклад, автомобілі, має тенденцію бути еластичним. Якщо ціна піде вгору, люди просто не купуватимуть машини прямо зараз, а дохід впаде.
Компанія знаходить\( q \) попит тисячами на їхні повітряні\( q=400-p^2 \) змії за ціною\( p \) доларів. Знайдіть еластичність попиту, коли ціна становить 5 доларів, а ціна - 15 доларів. Тоді знайдіть ціну, яка дозволить максимізувати дохід.
Рішення
Обчислення похідної,\( \frac{dq}{dp}=-2p \). Рівняння пружності як функція\( p \) буде:\[ E=\left| \frac{p}{q}\cdot\frac{dq}{dp} \right|=\left| \frac{p}{400-p^2}\cdot (-2p) \right| =\left| \frac{-2p^2}{400-p^2} \right| \nonumber \]
Оцінюючи це, щоб знайти еластичність на рівні 5 доларів та 15 доларів:
\[ E(5) = \left| \frac{-2(5)^2}{400-(5)^2} \right| \approx 0.133 \nonumber \]Тож попит нееластичний, коли ціна становить 5 доларів.
При ціні в 5 доларів зростання ціни на 1% зменшить попит лише на 0,13%. Дохід може бути підвищений за рахунок зростання цін.
\[ E(15) = \left| \frac{-2(15)^2}{400-(15)^2} \right| \approx 2.571 \nonumber \]Тож попит еластичний, коли ціна становить 15 доларів.
При ціні 15 доларів зростання ціни на 1% зменшить попит на 2,571%. Дохід може бути підвищений за рахунок зниження цін.
Щоб максимізувати дохід, ми могли б вирішити, коли\( E = 1 \):\[ \begin{align*} \left| \frac{-2p^2}{400-p^2} \right| & = 1 \\ 2p^2 & = 400-p^2 \\ 3p^2 & = 400 \\ p & = \sqrt{\frac{400}{3}}\approx 11.55. \end{align*} \nonumber \]
Ціна $11.55 дозволить максимізувати дохід.
Як ви бачили в останньому прикладі, еластичність забезпечує ще один спосіб визначити ціну, яка дозволить максимізувати дохід, враховуючи функцію попиту. Це не швидше або простіше, ніж методи, вивчені раніше в курсі, але ви можете використовувати будь-яку техніку.
