2.3: Похідна
- Page ID
- 60346
Визначення похідної
При роботі з лінійними функціями ми могли знайти нахил лінії, щоб визначити швидкість, з якою функція змінюється. Для довільної функції ми можемо визначити середню швидкість зміни функції. Це нахил січної лінії через ці дві точки на графіку.
Середня швидкість зміни =\( \dfrac{\Delta \text{output}}{\Delta \text{input}} = \dfrac{f(b) - f(a)}{b-a}\)
= нахил січної лінії через дві точки\(\left(a, f(a)\right)\) і\(\left(b, f(b)\right)\)
Припустимо, загальна собівартість виробництва\(x\) виробів дається по\(TC(x) = 200+30x-0.1x^2\). Визначте середню норму зміни собівартості при збільшенні виробництва з 25 одиниць до 100 одиниць.
Рішення
Вартість при виробництві 25 одиниць становить\(TC(25) = 200+30(25)-0.1(25)^2 = \$887.50\)
Вартість при виробництві 100 одиниць становить\(TC(100) = 200+30(100)-0.1(100)^2 = \$2200\)
Вартість зросла на $2200-$887,50 = $1312,50, тоді як виробництво збільшилося на 100 — 25 = 75 одиниць. Середня швидкість зміни становить:
\[\frac{TC(100) - TC(25)}{100 - 25} = \frac{2200-887.50}{100-25} = \frac{1312.50}{75} = 17.50 \text{ dollars per unit}\nonumber \]
Це говорить нам про те, що в середньому вартість збільшується на $17.50 за кожну вироблену одиницю.
Середня швидкість зміни - це нахил січної лінії між (25, 887,50) і (100, 2200)
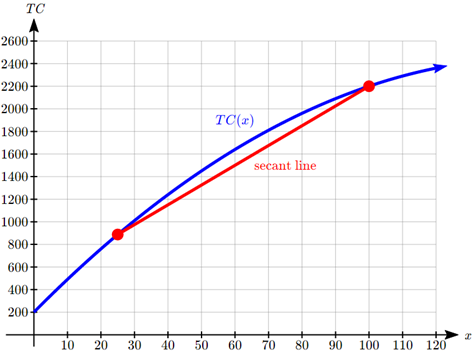
Думаючи про останній приклад, припустимо, що замість цього ми задали питання «Наскільки швидко зростають витрати, коли виробництво становить 25 одиниць?» Зверніть увагу, що це інший вид питання. Питання в прикладі задавалося про швидкість зміни протягом інтервалу, так як виробництво збільшувалося від одного значення до іншого. Це питання знову запитує швидкість зміни, але миттєву швидкість зміни, в конкретний момент.
У нас ще немає способу обчислення швидкості зміни, крім інтервалу. У наступному прикладі ми розглянемо пару способів оцінки миттєвої швидкості зміни.
Припустимо, загальна собівартість виробництва\(x\) виробів дається по\(TC(x) = 200+30x-0.1x^2\). Оцініть миттєву швидкість зміни, коли виробляються 25 найменувань.
Рішення
На попередньому графіку ми бачимо, що січний нахил на інтервалі не\(25\leq x \leq 100\) є особливо хорошою оцінкою миттєвої швидкості зміни, оскільки функція витрат здається крутішою\(x = 25\) тоді над січним нахилом. Ми могли б покращити оцінку, вибравши менший інтервал.
Підхід 1: Використання менших інтервалів
Використовуючи інтервал\(25\leq x \leq 30\), середня швидкість зміни становила б:
\[\frac{TC(30) - TC(25)}{30 - 25} = \frac{1010-887.50}{30-25} = \frac{122.50}{5} = 24.50 \text{ dollars per unit}\nonumber \]
Використовуючи інтервал з іншого боку\(20\leq x \leq 25\), середня швидкість зміни становила б:
\[\frac{TC(25) - TC(20)}{25 - 20} = \frac{887.50-760}{25-20} = \frac{127.5}{5} = 25.50 \text{ dollars per unit}\nonumber \]
Візуально ми бачимо, що обидві ці січні лінії, здається, наближаються до функції досить добре.
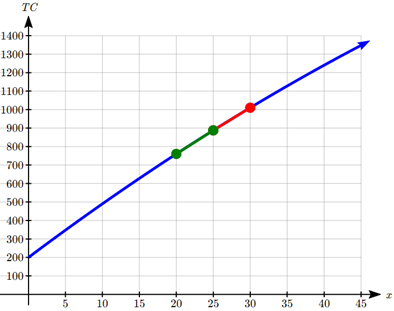
Ми очікуємо, що миттєва швидкість зміни буде десь між цими двома значеннями. Усереднивши їх, отримуємо оцінку в $25 за одиницю для миттєвої швидкості зміни.
Підхід 2: Оцінка за графіком.
Цей підхід частіше використовується, коли ми маємо лише графік функції, і не маємо формули для оцінки, але ми проілюструємо його тут, використовуючи ту ж функцію.
Миттєва швидкість зміни - це нахил дотичної лінії, яка є лінією, яка просто торкається графіка в цікавій точці, і має таку ж швидкість зміни (нахил), що і функція в точці. Враховуючи графік, ми можемо малювати в дотичній лінії, утримуючи лінійку до графіка та малюючи лінію, яка торкається графіка, коли\(x = 25\) і має однаковий нахил.
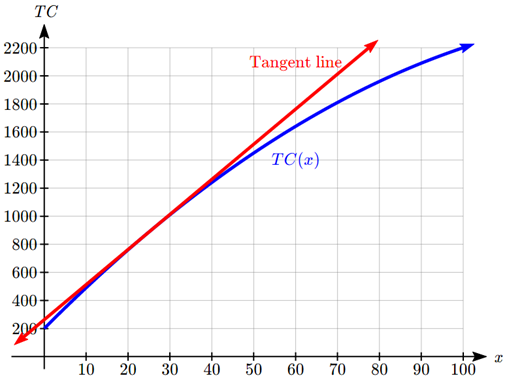
Щоб оцінити миттєву швидкість зміни, тепер ми можемо обчислити нахил цієї втягнутої лінії. Дивлячись на графік, дотична лінія, здається, проходить приблизно через (30, 1000) та (70, 2000), що дасть нахил\(\frac{2000-1000}{70-30}=\frac{1000}{40}=25\) доларів за одиницю.
Далі ми вивчимо ті ж ідеї, використовуючи функцію, визначену в таблиці, і в іншому контексті.
Припустимо, ми скидаємо помідор з вершини будівлі 100 футів і час його падіння.
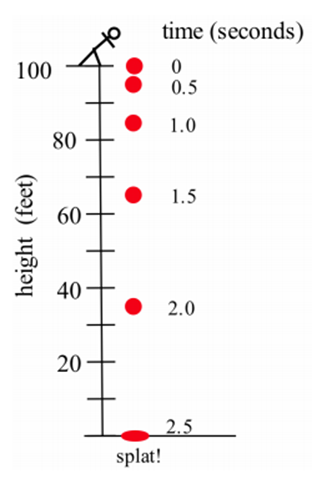
|
Час (сек) |
Висота (фути) |
|---|---|
|
0.0 |
100 |
|
0.5 |
96 |
|
1.0 |
84 |
|
1.5 |
64 |
|
2.0 |
36 |
|
2.5 |
0 |
- Скільки часу знадобилося, щоб помідор впав на 100 футів?
- Як далеко впав помідор протягом першої секунди?
- Як далеко впав помідор протягом останньої секунди?
- Як далеко помідор впав між\(t =0.5\) і\(t = 1\)?
- Якою була середня швидкість помідор під час його падіння?
- Якою була середня швидкість між\( t=1\)\(t=2\) секундами?
- Як швидко помідор падав через 1 секунду після того, як його скинули?
Рішення
На деякі з цих питань досить легко відповісти, в той час як деякі більш складні.
- Зі столу знадобилося 2,5 секунди, щоб помідор впав на 100 футів
- Протягом першої секунди помідор впав на 100 - 84 = 16 футів
- Протягом останньої секунди помідор впав на 64 - 0 = 64 фути
- Між\(t =0.5\) і\(t = 1\) помідор впав 96 - 84 = 12 футів
- Швидкість схожа на швидкість, і є швидкістю зміни. Ми можемо обчислити середню швидкість так само, як ми робили середню швидкість зміни раніше.
\[\text{Average velocity}=\frac{\text{distance fallen}}{\text{total time}}=\frac{\Delta\text{position}}{\Delta\text{time}}=\frac{-100 \text{ ft}}{2.5 \text{ s}}=-40 \text{ ft/s}\nonumber \] - Між\( t=1\) і\(t=2\) секундами,\[\text{Average velocity}=\frac{\Delta\text{position}}{\Delta\text{time}}=\frac{36\text{ ft}- 84\text{ ft}}{2\text{ s} - 1\text{ s}}=\frac{-48 \text{ ft}}{1 \text{ s}}=-48 \text{ ft/s}\nonumber \]
- Це питання істотно відрізняється від двох попередніх питань про середню швидкість. Тут ми хочемо миттєву швидкість, швидкість в одну мить у часі. На жаль, помідор не оснащений спідометром, тому доведеться дати приблизну відповідь. Як і в нашому підході 1 в попередньому прикладі, ми оцінимо його за допомогою січних укосів.
Одне грубе наближення миттєвої швидкості через 1 секунду - це просто середня швидкість протягом усього падіння, -40 фут/с Але помідор повільно падав на початку і швидко ближче до кінця, тому оцінка «-40 ft/s» може бути або не може бути гарною відповіддю.
Ми можемо отримати кращу апроксимацію миттєвої швидкості\(t=1\) при розрахунку середніх швидкостей за короткий проміжок часу e поблизу\(t = 1\). Середня швидкість між\(t = 0.5\) і\(t = 1\) є\(\dfrac{-12\text{ feet}}{0.5\text{ s}} = -24\text{ ft/s}\), і середня швидкість між\(t = 1\) і\(t = 1.5\) є\(\dfrac{-20\text{ feet}}{0.5\text{ s}} = -40\text{ ft/s}\) таким чином, ми можемо бути розумно впевнені, що миттєва швидкість становить від -24 ft/s до -40 ft/s. середнє значення, —32 ft/s, було б хорошою оцінкою для r миттєва швидкість.
Загалом, чим коротше проміжок часу, за який ми обчислюємо середню швидкість, тим краще середня швидкість буде наближатися до миттєвої швидкості.
Середня швидкість за часовий інтервал дорівнює\( \dfrac{\Delta\text{position}}{\Delta\text{time}} \) нахилу січної лінії через дві точки на графіку висоти проти часу. Миттєва швидкість в певний час і висота - це нахил дотичної лінії до графіка в точці, заданій тим часом і висотою.
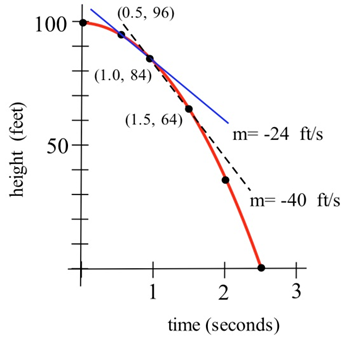
Середня швидкість =\( \dfrac{\Delta\text{position}}{\Delta\text{time}} \) = нахил січної лінії через 2 точки.
Миттєва швидкість = нахил прямої дотичної до графіка.
Припустимо, ми створили машину для підрахунку кількості бактерій, що ростуть на тарілці Петрі. Спочатку бактерій мало, тому популяція росте повільно. Тоді є більше бактерій, щоб розділити, щоб популяція росла швидше. Пізніше для зростаючої популяції стає більше бактерій і менше місця та поживних речовин, тому популяція знову зростає повільно. Нарешті, бактерії витратили більшу частину поживних речовин, і популяція зменшується, оскільки бактерії гинуть.
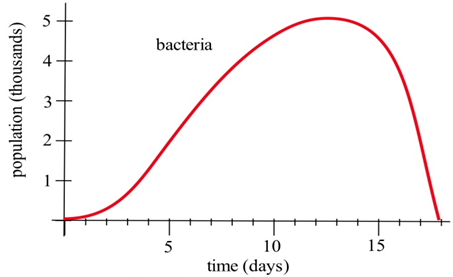
Використовуйте графік чисельності населення, щоб оцінити відповідь на наведені нижче запитання.
- Яка популяція бактерій в тимчасові\(t = 3\) дні?
- Що таке приріст населення від\(t = 3\) до\(t =10\) днів?
- Який темп приросту населення від 5\(t = 3\) до\(t = 10\) днів?
- Які темпи приросту населення на третій день, на\(t = 3\)?
Рішення
- З графіка, в\(t = 3\), популяція становить близько 0,5 тисячі, або 500 бактерій.
- При\(t = 10\), популяція становить близько 4,5 тисяч, тому приріст становить близько 4000 бактерій.
- Темпи зростання від\(t = 3\) до\(t = 10\) - це середні темпи зміни чисельності населення за цей час:\[ \begin{align*} \text{average change in population } & = \frac{\text{change in population}}{\text{change in time}}\\ & = \frac{\Delta\text{population}}{\Delta\text{time}} \\ & = \frac{4000\text{ bacteria}}{7\text{ days}} \\ & \approx 570\text{ bacteria/day}. \end{align*} \nonumber \]
Це нахил січної лінії через дві точки (3, 500) і (10, 4500).
- Це питання ставиться до миттєвої швидкості зміни населення, нахилу лінії, яка є дотичною до кривої населення при (3, 500). Якщо ми намалюємо лінію, приблизно дотичну до кривої в (3500) і виберемо дві точки біля кінців сегмента дотичної лінії, ми можемо оцінити, що миттєва швидкість приросту населення становить приблизно 320 бактерій на добу.
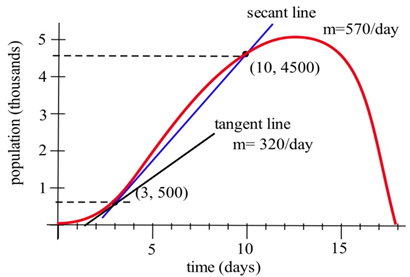
У попередніх прикладах ми помітили, що коли інтервал став меншим і меншим, січна лінія наближалася до дотичної лінії, а її нахил наближався до нахилу дотичної лінії. Це гарна новина — ми знаємо, як знайти нахил січної лінії.
Давайте вивчимо далі цю ідею знаходження дотичного нахилу на основі січного схилу.
Знайдіть нахил\(L\) прямої на графіку нижче, яка є\(f(x) = x^2\) дотичною до точки (2,4).
Ми могли б оцінити нахил\(L\) з графіка, але ми не будемо. Замість цього ми будемо використовувати ідею, що січні лінії через крихітні інтервали наближають дотичну лінію.
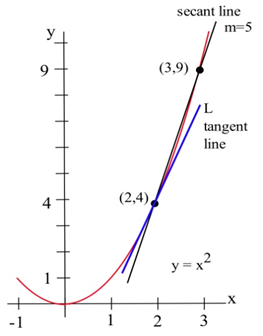
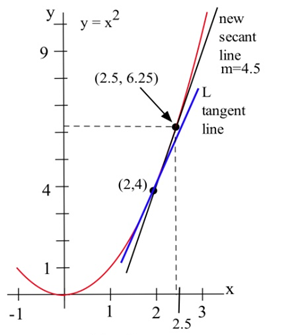
Ми бачимо, що лінія через (2,4) і (3,9) на графіку\(f\) є наближенням нахилу дотичної лінії, і ми можемо обчислити цей нахил точно:\(m = \frac{\Delta y}{\Delta x} = \frac{9-4}{3-2} = 5\). Але\(m = 5\) це лише оцінка нахилу дотичної лінії і не дуже хороша оцінка. Він занадто великий. Ми можемо отримати кращу оцінку, вибравши другу точку на графіку\(f\), яка ближче до (2,4). Точка (2,4) закріплена, і вона повинна бути однією з точок, які ми використовуємо.
З другого малюнка ми бачимо, що нахил прямої через точки (2,4) і (2,5,6,25) є кращим наближенням нахилу дотичної лінії в (2,4):\(m = \frac{\Delta y}{\Delta x} = \frac{6.25 - 4}{2.5 - 2} = \frac{2.25}{0.5} = 4.5 \), краща оцінка, але все ж наближення. Ми можемо продовжувати підбирати точки ближче і ближче до (2,4) на графіку\(f\), а потім обчислювати нахили ліній через кожну з цих точок і точку (2,4):
| \( x \) | \( y=x^2 \) | Ухил лінії наскрізь\( (x,y) \) і (2,4). |
| 1.5 | 2.25 | 3.5 |
| 1.9 | 3.61 | 3.9 |
| 1,99 | 3 9601 | 3.99 |
| \( x \) | \( y=x^2 \) | Ухил лінії наскрізь\( (x,y) \) і (2,4). |
| 3 | 9 | 5 |
| 2.5 | 6.25 | 4.5 |
| 2.01 | 4.0401 | 4.01 |
Єдине, що особливе в\(x\) —values ми вибрали, це те, що вони є числами, які близькі і дуже близькі до\(x = 2\). Хтось інший, можливо, вибрав інші значення поблизу для\(x\). Коли точки, які ми вибираємо, стають все ближче і ближче до точки (2,4) на графіку\( y = x^2\), нахили ліній через точки і (2,4) є кращими наближеннями нахилу дотичної лінії, і ці схили стають все ближче і ближче до 4.
Ми можемо обійти більшу частину обчислення, не вибираючи точки по черзі: давайте подивимося на загальну точку поблизу (2,4). Визначити\( x = 2 + h\) так\(h\) це приріст від 2 до\(x\). Якщо\(h\) невеликий, то\(x = 2 + h\) близький до 2 і точка\((2+h, f(2+h) ) = \left(2+h, (2+h)^2\right) \) близька до (2,4). Нахил\(m\) прямої через точки (2,4) і\(\left(2+h, (2+h)^2\right)\) являє собою хороше наближення нахилу дотичної лінії в точці (2,4):
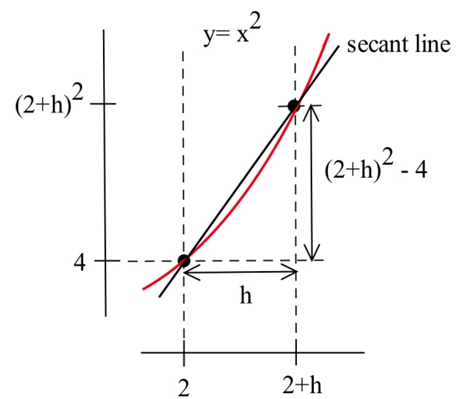
Ми можемо розрахувати січний ухил для будь-якого значення\(h\):
\[ m = \frac{\Delta y}{\Delta x} = \frac{(2+h)^2-4}{(2+h)-2} = \frac{\left(4+4h+h^2\right)-4}{h} = \frac{4h+h^2}{h} = \frac{h(4+h)}{h} = 4+h \nonumber\]
\( m = 4 + h \)Величина - нахил січної лінії через дві точки (2,4) і\(\left( 2+h, (2+h)^2 \right)\). Коли\(h\) стає все менше і менше, цей нахил наближається до нахилу дотичної лінії до графіка\(f\) at (2,4).
Більш формально ми могли б написати:\[\text{Slope of the tangent line} = \lim\limits_{h\to 0} \dfrac{\Delta y}{\Delta x} = \lim\limits_{h\to 0} (4+h). \nonumber \]
Ми можемо легко оцінити цю межу, використовуючи пряму підстановку, виявивши, що, коли інтервал\(h\) скорочується до 0, січний нахил наближається до дотичного нахилу, 4.
Скористайтеся аплетом нижче, щоб вивчити це. Ви можете перетягнути базову точку на графіку, щоб вивчити поведінку в різних місцях на графіку. Після встановлення базової точки використовуйте повзунок, щоб побачити, як січні лінії наближаються до дотичної лінії, коли\(h\) наближаються до нуля.
Знаходження дотичних нахилів і знаходження миттєвої швидкості зміни - одна і та ж проблема. У кожній задачі ми хотіли знати, як швидко щось змінюється в одну мить часу, і відповідь виявилося знаходженням нахилу дотичної лінії, яку ми наблизили з нахилом січної лінії. Ця ідея є ключем до визначення нахилу кривої.
Ми можемо розглядати похідну по-різному. Ось три з них:
- Похідна функції\(f\) в точці\((x, f(x))\) - це миттєва швидкість зміни.
- Похідна - це нахил дотичної прямої до графіка\(f\) в точці\((x, f(x))\).
- Похідна - це нахил кривої\(f(x)\) в точці\((x, f(x))\).
Функція називається диференційованою,\((x, f(x))\) якщо її похідна існує в\((x, f(x))\).
Позначення для похідної
Похідна по відношенню до\(x\) пишеться як\[f'(x)\nonumber \] (читати вголос як "\(f\)просте від\(x\) «), або\[y'\nonumber \] (читати вголос як «чому просте») або\[\frac{dy}{dx}\nonumber \] (читати вголос як «dee why dee ex»), або\(y = f(x)\)\[\frac{df}{dx}.\nonumber \]
Позначення, що нагадує дріб, називають позначенням Лейбніца. У ньому відображається не тільки назва функції (\(f\)або\(y\)), але і ім'я змінної (в даному випадку,\(x\)). Це виглядає як дріб, тому що похідна - це нахил. Насправді це просто\( \frac{\Delta y}{\Delta x} \) пишеться латинськими літерами замість грецьких букв.
Форми дієслова
Знаходимо похідну функції, або беремо похідну функції, або диференціюємо функцію.
Ми використовуємо адаптацію\( \frac{df}{dx} \) позначення, щоб означати «знайти похідну від\(f(x)\):»\[\frac{d}{dx}\left[f(x)\right]=\frac{df}{dx}.\nonumber \] [Книга використовує дужки замість дужок — обидві є прийнятними формами позначення.]
Формальне алгебраїчне визначення
\[f'(x)=\lim\limits_{h\to 0} \dfrac{f(x+h)-f(x)}{h}\nonumber \]
Практичне визначення
Похідна може бути апроксимована, дивлячись на середню швидкість зміни або нахил січної лінії, протягом дуже крихітного інтервалу. Чим менше інтервал, тим ближче це до істинної миттєвої швидкості зміни, нахилу дотичної лінії або нахилу кривої.
Забігаючи вперед
Незабаром у нас з'являться методи обчислення точних значень похідних з формул. Якщо функція дана вам у вигляді таблиці або графіка, вам все одно потрібно буде наблизити таким чином.
Це основа для решти цієї глави. Примітно, що така проста ідея (нахил дотичної лінії) і таке просте визначення (для похідної\( f'(x) \)) призведе до такої кількості важливих ідей і застосувань.
Знайти нахил дотичної лінії до\( f(x)=\frac{1}{x} \) at\(x = 3\).
Рішення
Нахил дотичної лінії - це величина похідної\(f'(3)\). \( f(3)=\frac{1}{3}\)і\( f(3+h)=\frac{1}{3+h} \), таким чином, використовуючи формальне граничне визначення похідної,\[ f'(3)=\lim\limits_{h\to 0}\frac{f(3+h)-f(3)}{h}=\lim\limits_{h\to 0}\frac{\frac{1}{3+h}-\frac{1}{3}}{h}. \nonumber \]
Ми можемо спростити, надавши дроби спільний знаменник:\[ \begin{align*} \lim\limits_{h\to 0}\frac{\frac{1}{3+h}-\frac{1}{3}}{h} & = \lim\limits_{h\to 0}\frac{\frac{1}{3+h}\cdot\frac{3}{3}-\frac{1}{3}\cdot\frac{3+h}{3+h}}{h} \\ & = \lim\limits_{h\to 0}\frac{\frac{3}{9+3h}-\frac{3+h}{9+3h}}{h} \\ & = \lim\limits_{h\to 0}\frac{\frac{3-(3+h)}{9+3h}}{h} \\ & = \lim\limits_{h\to 0}\frac{\frac{3-3-h}{9+3h}}{h} \\ & = \lim\limits_{h\to 0}\frac{\frac{-h}{9+3h}}{h} \\ & = \lim\limits_{h\to 0}\frac{-h}{9+3h}\cdot\frac{1}{h} \\ & = \lim\limits_{h\to 0}\frac{-1}{9+3h} \\ \end{align*} \] а оцінювати за допомогою прямої підстановки:\[\lim\limits_{h\to 0}\frac{-1}{9+3h}=\frac{-1}{9+3(0)}=-\frac{1}{9}.\nonumber \]
Таким чином, нахил дотичної лінії до\( f(x)=\frac{1}{x} \) at\(x = 3\) дорівнює\( -\frac{1}{9} \).
Похідна як функція
Тепер ми знаємо, як знайти (або принаймні приблизну) похідну функції для будь-якого\(x\) -значення; це означає, що ми можемо думати про похідну як функцію, теж. Входи однакові\(x\); вихід - це значення похідної при цьому\(x\) значенні.
Нижче наведено графік функції\( y=f(x) \). Ми можемо використовувати інформацію на графіку, щоб заповнити таблицю, що показує значення\( f'(x): \)
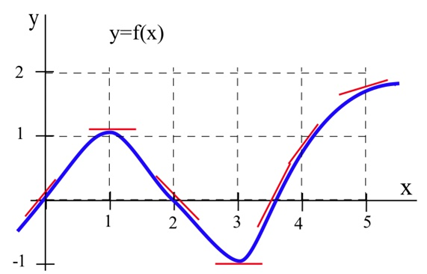
При різних значеннях\(x\), намалюйте найкращу здогадку на дотичній лінії і виміряйте її нахил. Можливо, вам доведеться розширити свої рядки, щоб ви могли прочитати деякі моменти. Загалом, ваша оцінка ухилу буде краще, якщо ви виберете точки, які легко читаються і віддалені один від одного. Ось оцінки для кількох значень\(x\) (частини використовуваних дотичних ліній наведені вище на графіку):
| \( x \) | \( y=f(x) \) | \( f'(x)= \)розрахунковий нахил дотичної лінії до кривої в точці\( (x,y) \). |
| 0 | 0 | 1 |
| 1 | 1 | 0 |
| 2 | 0 | -1 |
| 3 | -1 | 0 |
| 3.5 | 0 | 2 |
Ми можемо оцінити значення\(f'(x)\) при деяких нецілих значеннях\(x\), теж:\(f'(0.5) \approx 0.5\) і\(f'(1.3) \approx -0.3\).
Ми можемо навіть думати про цілі інтервали. Наприклад, якщо\(0 \lt x \lt 1\),\(f(x)\) то збільшується, всі схили позитивні,\(f'(x)\) а значить позитивні.
Значення\(f'(x)\) виразно залежать від значень\(x\), і\(f'(x)\) є функцією\(x\). Ми можемо використовувати результати в таблиці, щоб допомогти намалювати графік\(f'(x)\).
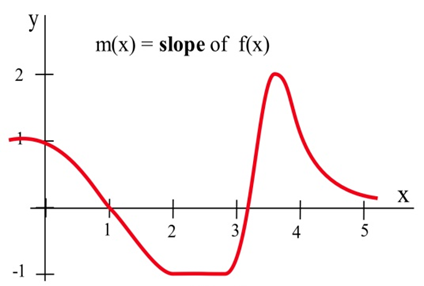
Щоб краще відчути це, вивчіть аплет нижче. Верхній графік - це графік вихідної функції\(g(x)\). Нижній графік показує нахили\(g(x)\), так і графік похідної,\(g'(x)\). Перетягніть точку а і зверніть увагу, як нахил дотичної лінії відповідає значенню похідної\(g'(x)\).
Показаний графік висоти\(h(t)\) ракети в часі\(t\).
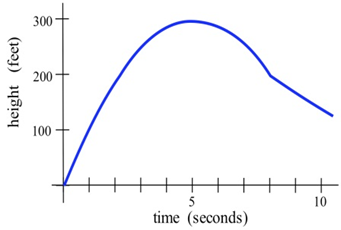
Намалюйте графік швидкості руху ракети в часі\(t\). (Швидкість є похідною від функції висоти, тому це нахил дотичної до графіка положення або висоти.)
Ми можемо оцінити нахил функції в декількох точках. На нижньому графіку нижче показана швидкість руху ракети. Це і є\(v(t) = h'(t)\).
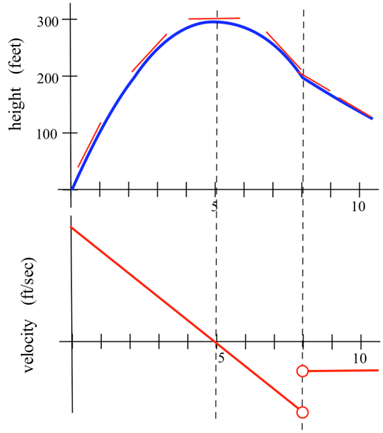
У деяких додатках нам потрібно знати, де графік функції\(f(x)\) має горизонтальні дотичні лінії (нахили = 0).
Нижче наведено графік\(y = g(x)\). При яких значеннях графа\(x\)\(g(x)\) має горизонтальні дотичні лінії?
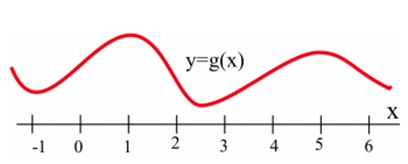
Дотичні лінії до графіка\(g(x)\) є горизонтальними (нахил = 0), коли\(x\approx -1, 1, 2.5, \text{ and } 5\).
Ми також можемо знайти похідні функції алгебраїчно з використанням обмежень.
Знайти\( \frac{d}{dx}\left( 2x^2-4x-1 \right) \).
Налаштування похідної з використанням ліміту,\[ f'(x)=\lim\limits_{h\to 0}\frac{f(x+h)-f(x)}{h}.\nonumber \]
Почнемо зі спрощення,\( f(x+h) \) розширивши:\[ \begin{align*} f(x+h) & = 2(x+h)^2-4(x+h)-1 \\ & = 2(x^2+2xh+h^2)-4(x+h)-1 \\ & = 2x^2+4xh+2h^2-4x-4h-1 \end{align*} \nonumber \]
Тепер знаходимо межу:\[ \begin{align*} f'(x) & = \lim\limits_{h\to 0}\frac{f(x+h)-f(x)}{h} \\ & = \lim\limits_{h\to 0} \frac{(2x^2+4xh+2h^2-4x-4h-1)-(2x^2-4x-1)}{h} \\ & = \lim\limits_{h\to 0} \frac{2x^2+4xh+2h^2-4x-4h-1-2x^2+4x+1}{h} \qquad \text{(Substitute in the formulas.)} \\ & = \lim\limits_{h\to 0} \frac{4xh+2h^2-4h}{h} \qquad \text{(Now simplify.)}\\ & = \lim\limits_{h\to 0} \frac{h(4x+2h-4)}{h} \qquad \text{(Factor out the \( h \), then cancel.)} \\ & = \lim\limits_{h\to 0} (4x+2h-4) \end{align*} \nonumber \] Ми можемо знайти межу цього виразу шляхом прямої підміни:\[ f'(x)=\lim\limits_{h\to 0} (4x+2h-4)=4x-4\nonumber \]
Зверніть увагу, що похідна залежить від\(x\), і що ця формула скаже нам нахил дотичної лінії до\(f\) будь-якого значення\(x\). Наприклад, якби ми хотіли знати дотичний нахил\(f\) at\(x = 3\), ми б просто оцінили:\( f'(3)=4(3)-4=8 \).
Формула для похідної функції дуже потужна, але, як бачите, обчислення похідної з використанням визначення межі дуже трудомісткий. У наступному розділі ми виділимо деякі закономірності, які дозволять нам почати будувати набір правил пошуку похідних без необхідності визначення межі.
Тлумачення похідної
Поки що ми підкреслювали похідну як нахил прямої дотичної до графіка. Ця інтерпретація дуже наочна та корисна при вивченні графіка функції, і ми будемо продовжувати її використовувати. Похідні, однак, використовуються в самих різних областях і додатках, і деякі з цих полів використовують інші інтерпретації. Нижче наведено кілька інтерпретацій похідної, які зазвичай використовуються.
Загальний
Швидкість зміни:\(f '(x)\) швидкість зміни функції на\(x\). Якщо одиниці для\(x\) - це роки, а одиниці для\(f(x)\) - це люди, то одиниці для\( \frac{df}{dx} \) є\(\frac{\text{people}}{\text{year}}\), швидкість зміни чисельності населення.
Графічний
Нахил:\(f '(x)\) нахил прямої дотичної до графіка\(f\) в точці\(( x, f(x) )\).
Фізичні
Швидкість: Якщо\(f(x)\) це положення об'єкта в часі\(x\), то\(f '(x)\) це швидкість об'єкта в той час\(x\). Якщо одиниці для\(x\) годин і\(f(x)\) відстань вимірюється в милі, то одиниці для\(\mathbf{f '}(x) = \frac{df}{dx}\) є\( \frac{\text{miles}}{\text{hour}} \), милі на годину, що є мірою швидкості.
Прискорення: Якщо\(f(x)\) швидкість об'єкта в часі\(x\), то\(f '(x)\) це прискорення об'єкта в часі\(x\). Якщо одиниці для\(x\) є годинами і\(f(x)\) має одиниці\( \frac{\text{miles}}{\text{hour}} \), то одиниці для прискорення\(\mathbf{f '(x)} = \frac{df}{dx}\) є\( \frac{\text{miles/hour}}{\text{hour}} =\frac{\text{miles}}{\text{hour}^2} \), милі на годину на годину.
Бізнес
Маржинальні витрати, граничний дохід та маржинальний прибуток: ми розглянемо ці терміни більш глибоко пізніше в розділі. В основному гранична вартість становить приблизно додаткові витрати на виготовлення ще одного об'єкта після того, як ми вже зробили\(x\) об'єкти. Якщо одиниці для\(x\) велосипедів, а одиниці для\(f(x)\) - долари, то одиниці для\(f '(x) = \frac{df}{dx}\) є\( \frac{\text{ dollars}}{\text{ bicycle}} \), вартість за велосипед.
У бізнес-контексті слово "граничний" зазвичай означає похідну або швидкість зміни деякої кількості.
Однією з сильних сторін обчислення є те, що він забезпечує єдність та економію ідей серед різноманітних застосувань. Словниковий запас і проблеми можуть бути різними, але ідеї і навіть позначення числення все одно корисні.
Припустимо, крива попиту на віджети була задана\( D(p)=\frac{1}{p} \), де\(D\) кількість віджетів, в тисячах, за ціною\(p\) доларів. Інтерпретувати\(D\) похідну від\(p = \) $3.
Зверніть увагу, що ми розраховували\( D'(3) \) раніше бути\( D'(3)=-\frac{1}{9}\approx -0.111 \).
Оскільки\(D\) має одиниці тисячі віджетів
, а одиниці для\(p\) - доларів ціни, одиниці для\(D'\) будуть\( \frac{\text{thousands of widgets}}{\text{dollar of price}} \). Іншими словами, це показує, як зміниться попит у міру зростання ціни.
Зокрема,\( D'(3)\approx -0.111 \) говорить нам, що коли ціна складе 3 долари, попит зменшиться приблизно на 0,111 тисяч предметів за кожен долар, який ціна зростає.
(Примітка. Знімки екрана в наступному відео взяті з попередньої версії книги, тому деякі номери розділів або заголовки можуть виглядати не однаково. Однак значна частина контенту однакова, а коментарі все ще застосовуються.)
