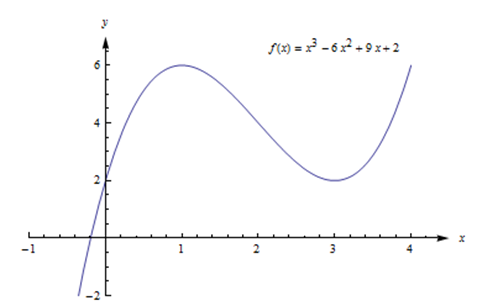
2.8: Оптимізація
- Page ID
- 60382
У теорії та додатках ми часто хочемо максимізувати або мінімізувати деяку кількість. Інженер може захотіти максимізувати швидкість нового комп'ютера або мінімізувати тепло, вироблене приладом. Виробник може захотіти максимізувати прибуток і частку ринку або мінімізувати відходи. Студент може захотіти максимізувати оцінку в обчисленні або мінімізувати години навчання, необхідні для отримання певної оцінки.
Без обчислення ми знаємо, як знайти оптимальні точки лише в декількох конкретних прикладах (наприклад, ми знаємо, як знайти вершину параболи). Але що робити, якщо нам потрібно оптимізувати незнайому функцію?
Найкращий спосіб, який ми маємо без числення, - це вивчити графік функції, можливо, використовуючи технологію. Але наш погляд залежить від обраного нами оглядового вікна - ми можемо пропустити щось важливе. Крім того, ми, мабуть, отримаємо лише наближення таким чином. (У деяких випадках це буде досить добре.)
Обчислення забезпечує способи різкого звуження кількості точок, які ми повинні вивчити, щоб знайти точні місця максимумів і мінімумів, в той же час гарантуючи, що ми не пропустили нічого важливого.
Локальні максими і мініми
Перш ніж ми вивчимо, як обчислення може допомогти нам знайти максимуми та мінімуми, нам потрібно визначити поняття, які ми будемо розробляти та використовувати.
\(f(x)\)має локальний максимум при\(x=a\) якщо\(f(a) \geq f(x)\) для всіх\(x\) поруч\(a\).
\(f(x)\)має локальний мінімум,\(x=a\) якщо\(f(a) \leq f(x)\) для всіх\(x\) поруч\(a\).
\(f(x)\)має локальну крайність при\(x=a\) якщо\(f(a)\) є локальним максимумом або мінімумом.
Множиною їх є максимуми і мінімуми. Ми часто просто говоримо «max» або «min»; це зберігає багато складів.
Деякі книги говорять «родич» замість «місцевий».
Процес знаходження максимумів або мінімумів називається оптимізацією.
Точка - це локальний max (або min), якщо він вище (нижче), ніж усі сусідні точки. Ці точки походять від форми графіка.
\(f(x)\)має глобальний максимум при\(x=a\) if\(f(a) \geq f(x)\) для всіх\(x\) у домені\(f(x)\).
\(f(x)\)має глобальний мінімум,\(x=a\) якщо\(f(a) \leq f(x)\) для всіх\(x\) у домені\(f(x)\).
\(f(x)\)має глобальну крайність,\(x=a\) якщо\(f(a)\) є глобальним максимумом або мінімумом.
Деякі книги говорять «абсолютний» замість «глобальний».
Точка є глобальним максимумом (або min), якщо вона вище (нижче), ніж кожна точка на графіку. Ці точки походять від форми графіка і вікна, через яке ми переглядаємо графік.
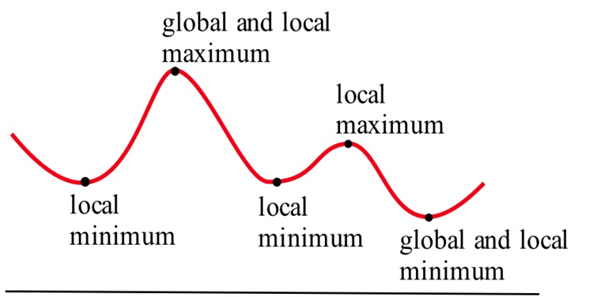
Позначені локальні та глобальні крайності функції на малюнку 1. Ви повинні помітити, що кожна глобальна крайність - це також локальна крайність, але є локальні крайнощі, які не є глобальними крайнощами.
Якщо\(h(x)\) висота землі над рівнем моря в місці розташування\(x\), то глобальним максимумом\(h\) є\(h\) (вершина гори. Еверест) = 29 028 футів. Місцевий максимум\(h\) для Сполучених Штатів є\(h\) (вершина гори. Мак-Кінлі) = 20 320 футів. Місцевий мінімум\(h\) для Сполучених Штатів становить\(h\) (Долина Смерті) = -282 футів.
У таблиці наведено щорічне обчислення зарахувань у великому університеті. Які роки мали локальні максимальні або мінімальні чисельні зарахування? Якими були глобальні максимальні та мінімальні зарахування в обчисленні?
| Рік | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 |
| Зарахування | 1257 | 1324 | 1378 | 1336 | 1389 | 1450 | 1523 | 1582 | 1567 | 1545 | 1571 |
Були місцеві максимуми в 2002 і 2007 роках; глобальний максимум становив 1582 студентів у 2007 році. Існували місцеві мінімуми у 2003 та 2009 роках; глобальний мінімум становив 1257 студентів у 2000 році. Ми вирішили не думати про 2000 як локальний мінімум або 2010 як локальний максимум; однак деякі книги будуть включати кінцеві точки. Нам дозволяється мати глобальний максимум або глобальний мінімум в кінцевій точці.
Знаходження максимумів та мінімумів функції
Як повинна виглядати дотична лінія при локальному max або min? Подивіться на ці два графіки ще раз — ви побачите, що у всіх крайніх точках дотична лінія горизонтальна (так\(f' = 0\)). На синьому графіку є один крок — дотична лінія вертикальна (так\(f'\) не визначена).
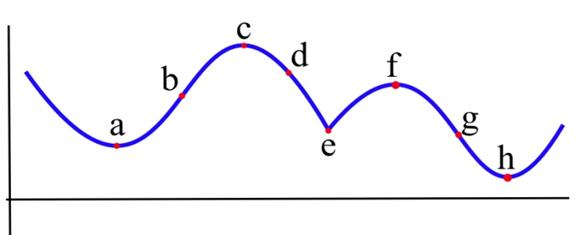
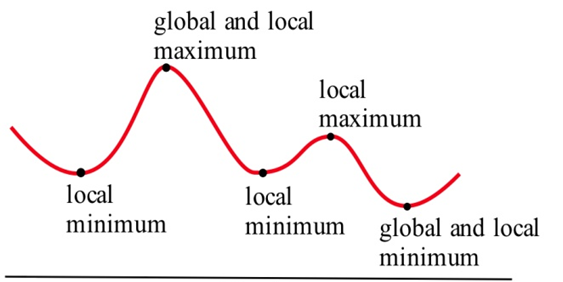
Це дає нам підказку, як знайти екстремальні значення.
Критичне число для функції\(f\) is a value \(x = a\) in the domain of \(f\) where either \(f'(a) = 0\) or \(f'(a)\) is undefined.
Критична точка для функції\(f\) is a point \((a, f(a))\) where a is a critical number of \(f\).
Локальний макс або хв\(f\) може відбуватися лише в критичній точці.
Знайдіть критичні точки\(f(x) = x^3 - 6x^2 + 9x + 2\).
Критичне число\(f\) може виникати тільки там, де\(f'(x) = 0\) або де\(f'\) не існує.
\[f '(x) = 3x^2 - 12x + 9 = 3(x^2 - 4x + 3) = 3(x - 1)(x - 3)\nonumber \]Так\(f'(x) = 0\) при\(x = 1\) і\(x = 3\) (і ніяких інших значень\( x \)). Немає місць, де\(f'\) не визначено.
Критичними числами є\(x = 1\) і\(x= 3\). Отже, критичними точками є (1, 6) і (3, 2).
Це єдино можливі місця розташування локальних крайнощів\(f\). Ми ще не обговорювали, як визначити, чи є будь-який з цих пунктів насправді локальною крайністю\(f\), або який він може бути. Але ми можемо бути впевнені, що жодна інша точка не є локальною крайністю.
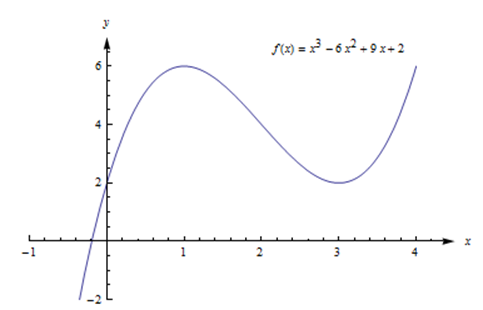
Графік\(f\) нижче показує, що\((1, f(1) ) = (1, 6)\) є локальним максимумом і\((3, f(3) ) = (3, 2)\) є локальним мінімумом. Ця функція не має глобального максимуму або мінімуму.
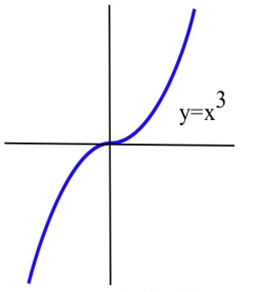
Знайти всі локальні крайнощі\(f(x) = x^3\).
\(f(x) = x^3\)диференційований для всіх\(x\), і\(f'(x) = 3x^2\). Єдине місце, де\(f'(x) = 0\) знаходиться\(x = 0\), тому єдиним кандидатом є критична точка (0,0).
Якщо\(x \gt 0\) тоді\(f(x) = x^3 \gt 0 = f(0)\), так не\(f(0)\) є локальним максимумом.
Аналогічно, якщо\(x \lt 0\) тоді\(f(x) = x^3 \lt 0 = f(0)\)\(f(0)\) так не локальний мінімум.
Критична точка (0,0) є єдиним кандидатом, щоб бути локальним екстремумом\(f\), і, виходячи з графіка, цей кандидат не виявився локальним екстремумом\(f\). Функція\(f(x) = x^3\) не має будь-яких локальних крайнощів.
Запам'ятайте цей приклад! Недостатньо знайти критичні точки — можна лише сказати, що у критичних точках\(f\) може бути локальна крайність.
Перший і другий похідні тести
Це критична точка Максимум або Мінімум (або Ні)?
Після того, як ми знайшли критичні точки\(f\), у нас все ще виникає проблема визначення, чи є ці точки максимумами, мінімумами чи ні.
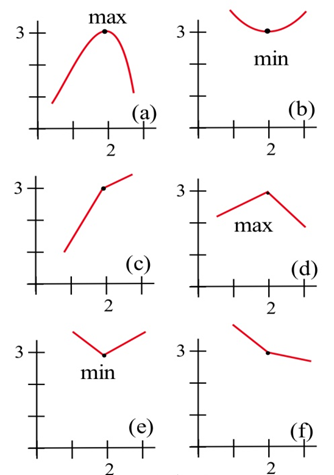
Всі графіки на малюнку нижче мають критичну точку в (2, 3). З графіків видно, що точка (2,3) є локальним максимумом в (а) і (d), (2,3) - локальний мінімум в (b) і (e), а (2,3) не є локальною крайністю в (c) і (f).
Критичні цифри дають лише можливі місця розташування крайнощів, а деякі критичні числа не є місцями крайнощів. Критичні цифри - це кандидати на місця розташування максимумів і мінімумів.
\(f'\)і екстремальні значення\(f\)
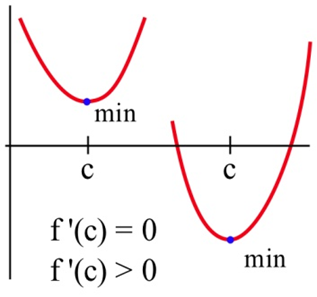
Тут показані чотири можливі форми графіків — на кожному графіку точка, позначена стрілкою, є критичною точкою, де\(f'(x) = 0\). Що відбувається з похідною поблизу критичної точки?

При локальному max, наприклад, на графіку зліва, функція збільшується зліва від локального max, потім зменшується праворуч. Похідна спочатку позитивна, потім негативна при локальному максі. При локальному min функція зменшується вліво і збільшується вправо, тому похідна спочатку негативна, потім позитивна. Коли локальної крайності немає, функція продовжує збільшуватися (або зменшуватися) прямо за критичною точкою - похідна не змінює знак.
Знайдіть критичні точки\(f\).
Для кожного\(c\) критичного числа огляньте знак зліва і праворуч від\(c\).\(f’\) Що відбувається зі знаком, коли ви рухаєтеся зліва направо?
- Якщо\(f'(x)\) змінюється від позитивного до негативного на\(x = c\), то\(f\) має локальний максимум при\((c, f(c))\).
- Якщо\(f'(x)\) змінюється від негативного до позитивного на\(x = c\), то\(f\) має локальний мінімум при\((c, f(c))\).
- Якщо\(f'(x)\) не змінює знак на\(x = c\), то не\((c, f(c))\) є ні локальним максимумом, ні локальним мінімумом.
Знайдіть критичні точки\(f(x) = x^3 - 6x^2 + 9x + 2\) і класифікуйте їх як локальні max, локальні min, або ні.
Ми вже знайшли критичні точки; вони є (1, 6) і (3, 2).
Тепер ми можемо використовувати перший похідний тест для класифікації кожного. Нагадаємо, що\(f'(x) = 3x^2 - 12x + 9 = 3(x^2 - 4x + 3) = 3(x - 1)(x - 3)\). З фактованою формою найпростіше працювати тут, тому давайте скористаємося цим.
На (1, 6) ми могли б вибрати число трохи менше 1, щоб підключити до формули для\(f'\) - можливо\(x = 0\), використовувати, або\(x = 0.9\). Тоді ми могли б розглянути його знак. Але ми не дбаємо про числове значення, все, що нас цікавить, - це його знак. І для цього нам не потрібно робити жодного підключення:
- Якщо\(x\) трохи менше 1, то\(x-1\) негативний, і\(x-3\) негативний. Так\(f' = 3(x - 1)(x - 3)\) буде pos (neg) (neg) = позитивний.
- Для\(x\) трохи більше 1, ми можемо оцінити\(f'\) число більше 1 (але менше 3, ми не хочемо пройти повз наступну критичну точку!) — можливо\(x = 2\). Або ми можемо зробити швидкий знак аргумент, як те, що ми зробили вище: для\(x\) трохи більше 1,\(f' = 3(x - 1)(x - 3)\) буде pos (pos) (neg) = негативний.
Так\(f'\) змінюється від позитивного до негативного, а це означає, що існує локальний макс при (1, 6).
Як інший підхід, ми могли б провести числову лінію і відзначити критичні числа:
Ми вже знаємо, що похідна дорівнює нулю або невизначена при критичних числах. На кожному проміжку між цими значеннями похідна буде залишатися одним і тим же знаком. Щоб визначити знак, ми могли б вибрати тестове значення в кожному інтервалі та оцінити похідну в цих точках (або використовувати підхід знаків, використаний вище).
При (3, 2)\(f'\) змінюється від негативного до позитивного, тому існує локальний min при (3, 2). Це підтверджує те, що ми бачили раніше на графіку.
\(f''\)і екстремальні значення\(f\)
Увігнутість функції також може допомогти нам визначити, чи є критична точка максимальною чи мінімальною чи ні. Наприклад, якщо точка знаходиться внизу увігнутої вгору функції, то точка мінімальна.
Знайти всі критичні точки\(f\). For those critical points where \(f'(c) = 0\), find \(f''(c)\).
- Якщо\(f''(c) \lt 0\) (негативний)\(f\) то увігнутий вниз і має локальний максимум при\(x = c\).
- Якщо\(f''(c) \gt 0\) (позитивний)\(f\) то увігнутий вгору і має локальний мінімум при\(x = c\).
- Якщо\(f''(c) = 0\) тоді\(f\) може бути локальний максимум, мінімум або ні на\(x = c\).
Мультфільм обличчя можуть допомогти вам згадати другий похідний тест.
\(f(x) = 2x^3 - 15x^2 + 24x - 7\)має критичні числа\(x =\) 1 і 4. Використовуйте другий тест похідних для екстремумів, щоб визначити, чи\(f(1)\)\(f(4)\) є максимумами чи мінімумами чи ні.
Нам потрібно знайти другу похідну:\[ \begin{align*} f(x) & = 2x^3 - 15x^2 + 24x - 7\\ f'(x) & = 6x^2 - 30x + 24\\ f''(x) & = 12x - 30 \end{align*} \nonumber \]
Тоді нам просто потрібно оцінити\(f''\) при кожному критичному числі:
\(x = 1\):\( f''(1)=12(1)-30 \lt 0 \), Таким чином, існує локальний максимум при\(x = 1\).
\(x = 4\):\( f''(4)=12(4)-30 \gt 0 \), Таким чином, існує локальний мінімум на\(x = 4\).
Багатьом студентам подобається другий похідний тест. Другий похідний тест часто простіший у використанні, ніж перший похідний тест. Вам потрібно знайти лише знак одного числа для кожного критичного числа, а не двох. І якщо ваша функція є поліном, його друга похідна, ймовірно, буде простіша функція, ніж похідна.
Однак, якщо вам потрібно було правило продукту, правило частки або правило ланцюга, щоб знайти першу похідну, пошук другої похідної може бути великою роботою. Крім того, навіть якщо друга похідна проста, другий похідний тест не завжди дає відповідь. Перший похідний тест завжди дасть вам відповідь.
Використовуйте будь-який тест, який ви хочете. Але пам'ятайте - ви повинні зробити певний тест, щоб переконатися, що ваша критична точка насправді є локальним макс або хв.
Глобальні максими та мінімуми
У додатках ми часто хочемо знайти глобальну крайність; знання того, що критична точка є локальною крайністю, недостатньо.
Наприклад, якщо ми хочемо отримати найбільший прибуток, ми хочемо отримати абсолютно найбільший прибуток з усіх. Як ми знаходимо глобальний макс і мін?
Є лише кілька додаткових речей, про які слід подумати.
Кінцеві крайності
Локальні крайності функції виникають у критичних точках - це точки функції, які ми можемо знайти, думаючи про форму (і використовуючи похідну, щоб допомогти нам). Але якщо ми дивимося на функцію на замкнутому інтервалі, кінцеві точки можуть бути крайності. Ці крайності кінцевих точок не пов'язані з формою функції; вони мають відношення до інтервалу, вікна, через яке ми переглядаємо функцію.
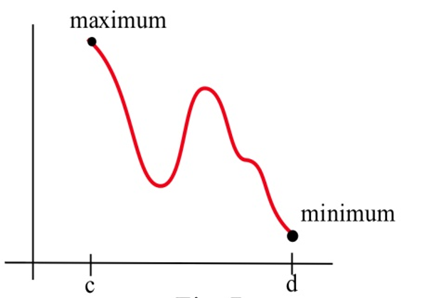
На графіку вище видно, що є три критичні точки - одна локальна хв, одна локальна макс, і одна, яка не є однією. Але глобальний максимум, найвища точка з усіх, знаходиться в лівій кінцевій точці. Глобальний хв, найнижча точка з усіх, знаходиться в правій кінцевій точці.
Як ми вирішуємо, чи кінцеві точки глобальні макс або хв? Це простіше, ніж ви очікували - просто підключіть кінцеві точки разом з усіма критичними числами та порівняйте\(y\) -значення.
Цю методику можна використовувати, коли ви намагаєтеся знайти глобальні екстремуми протягом обмеженого інтервалу.
Єдині місця, де функція може мати глобальну крайність на обмеженому інтервалі, знаходяться в критичних точках або кінцевих точках.
- Якщо функція має лише одну критичну точку, і це локальна крайність, то це також глобальна крайність.
- Якщо є кінцеві точки, знайдіть глобальні крайності, порівнявши\(y\) -значення у всіх критичних точках і в кінцевих точках.
- Якщо ви сумніваєтеся, графік функції, щоб бути впевненим. (Однак, якщо проблема явно не говорить вам про інше, недостатньо просто використовувати графік, щоб отримати відповідь.)
Знайти глобальні макс і хв\(f(x) = x^3 - 3x^2 - 9x + 5\) for\(-2 \leq x \leq 6\).
\(f'(x) = 3x^2 - 6x - 9 = 3(x + 1)(x - 3)\). Нам потрібно знайти критичні точки, і нам потрібно перевірити кінцеві точки.
\(f'(x) = 3(x + 1)(x - 3) = 0\)коли\(x = -1\) і\(x = 3\). Кінцевими точками інтервалу є\(x = -2\) і\(x = 6\).
Тепер ми просто порівняємо значення\(f\) при цих чотирьох значеннях\(x\):
| \( x \) | \( f(x) \) |
| -2 | 3 |
| -1 | 10 |
| 3 | -22 |
| 6 | 59 |
Глобальний мінімум\(f\) on\([ -2, 6]\) дорівнює -22, коли\(x = 3\), а глобальний максимум\(f\) on\([ -2, 6]\) дорівнює 59, коли\(x = 6\).
Будьте обережні! Ви можете використовувати цей метод (оцінюючи функцію в кінцевих точках і критичних значеннях) для визначення глобальних екстремумів протягом обмеженого інтервалу.
Якщо питання ставиться до локальної крайності, необхідно використовувати перший або другий похідний тест, описаний раніше в розділі.
Якщо є лише одна критична точка
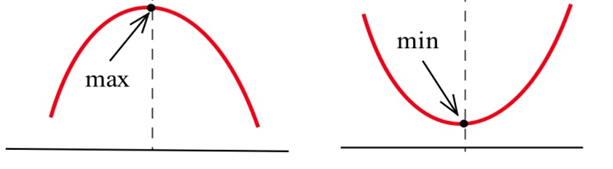
Якщо функція має тільки одну критичну точку і це локальний max (або min), то вона повинна бути глобальним max (або min). Щоб переконатися в цьому, подумайте про геометрію. Подивіться на графік зліва — є локальний макс, і графік опускається по обидві сторони від критичної точки. Припустимо, була якась інша точка, яка була вище — тоді графік повинен був би розвернутися. Але цей переломний момент виявився б ще одним критичним моментом. Якщо є лише одна критична точка, то графік ніколи не зможе повернутися назад.
Якщо ви сумніваєтеся, графікуйте його і подивіться.
Якщо ви намагаєтеся знайти глобальний max або min на відкритому інтервалі (або всю реальну лінію), а критичної точки більше однієї, то вам потрібно подивитися на графік, щоб вирішити, чи є глобальний max або min. Будьте впевнені, що всі ваші критичні точки відображаються на вашому графіку, і що ви графуєте за ними - це підкаже вам, що ви хочете знати.
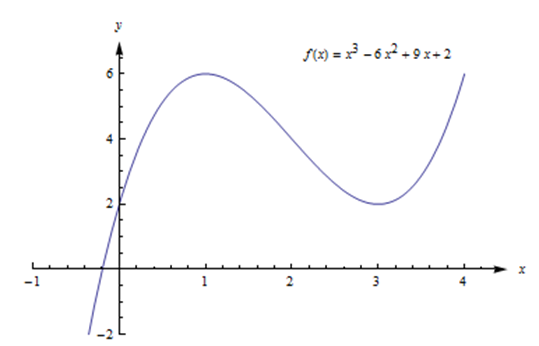
Знайти глобальні макс і хв\(f(x) = x^3 - 6x^2 + 9x + 2\).
Раніше ми виявили, що (1, 6) - це локальний макс, а (3, 2) - локальний хв. Це не замкнутий інтервал, і є дві критичні точки, тому ми повинні звернутися до графіка функції, щоб знайти глобальні max і min.
Графік\(f\) показує, що точки зліва від\(x = 4\) мають\(y\) -значення більше 6, тому (1, 6) не є глобальним максимумом. Так само, якщо\(x\)\(y\) негативний, менше 2, тому (3, 2) не є глобальним min. Кінцевих точок немає, тому ми вичерпали всі можливості. Ця функція не має глобального максимуму або мінімуму.