2.E: Похідна (вправи)
- Page ID
- 60347
2.1 Вправи
Використовуйте графік, щоб визначити наступні межі.
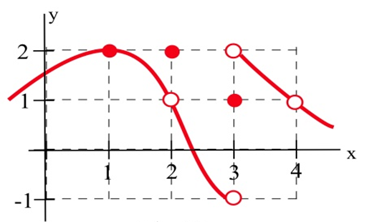
| а.\(\lim_{x \to 1} f(x)\) | б.\(\lim_{x \to 2} f(x)\) |
| c.\(\lim_{x \to 3} f(x)\) | д.\(\lim_{x \to 4} f(x)\) |
Використовуйте графік, щоб визначити наступні межі.
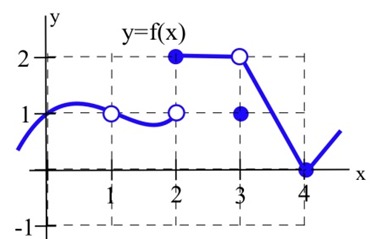
| а.\(\lim_{x \to 1} f(x)\) | б.\(\lim_{x \to 2} f(x)\) |
| c.\(\lim_{x \to 3} f(x)\) | д.\(\lim_{x \to 4} f(x)\) |
Оцінити
| а.\(\lim_{x \to 1} \frac{x^2+3x+3}{x-2}\) | б.\(\lim_{x \to 2} \frac{x^2+3x+3}{x-2}\) |
Оцінити
| а.\(\lim_{x \to 0} \frac{x+7}{x^2+9x+14}\) | б.\(\lim_{x \to 3} \frac{x+7}{x^2+9x+14}\) |
| c.\(\lim_{x \to 4} \frac{x+7}{x^2+9x+14}\) | д.\(\lim_{x \to 7} \frac{x+7}{x^2+9x+14}\) |
У яких точках функція показана переривчастою?
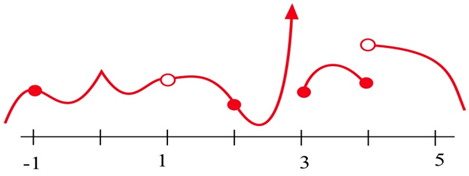
У яких точках функція показана переривчастою?
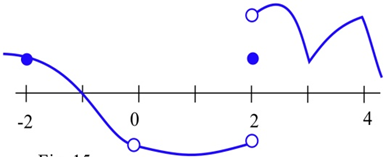
Знайдіть хоча б одну точку, в якій кожна функція не є безперервною, і станьте, яка з 3-х умов у визначенні неперервності порушена в цій точці.
| а.\(\frac{x+5}{x-3}\) | б.\(\frac{x^2+x-6}{x-2}\) | c.\(\frac{x}{x}\) |
| д.\(\frac{\pi}{x^2-6x+9}\) | е.\(\ln (x^2)\) |
2.2 Вправи
Що таке ухил лінії через (3,9) і\((x, y)\) для\(y = x^2\) і\(x = 2.97\)? \(x = 3.001\)? \(x = 3+h\)? Що відбувається з цим останнім нахилом, коли\(h\) дуже малий (близький до 0)? Намалюйте графік\(y = x^2\) для\(x\) близько 3.
Що таке ухил лінії через (—2,4) і\((x, y)\) для\(y = x^2\) і\(x = –1.98\)? \(x = –2.03\)? \(x = –2+h\)? Що відбувається з цим останнім нахилом, коли\(h \) дуже малий (близький до 0)? Намалюйте графік\(y = x^2\) для\(x\) ближнього —2.
Що таке ухил лінії через (2,4) і\((x, y)\) для\(y = x^2 + x – 2\) і\(x = 1.99\)?
\(x = 2.004\)? \(x = 2+h\)? Що відбувається з цим останнім ухилом, коли\(h\) він дуже малий? Намалюйте графік\(y = x^2 + x – 2\) для\(x\) поблизу 2.
Що таке нахил лінії через (—1, —2) і\((x, y)\) для\(y = x^2 +x – 2\) і\(x = –.98\)?
\(x = –1.03\)? \(x = –1+h\)? Що відбувається з цим останнім ухилом, коли\(h\) він дуже малий? Намалюйте графік\(y = x^2 + x – 2\) для\(x\) ближнього —1.
Графік праворуч показує температуру протягом доби в Еймсі.
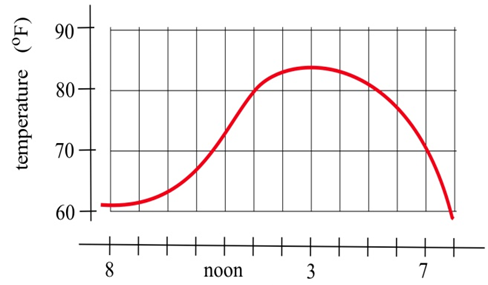
(а) Якою була середня зміна температури з 9 ранку до 1 вечора?
(б) Оцінити, наскільки швидко піднімалася температура в 10 ранку і о 7 вечора?
Графік показує відстань автомобіля від вимірювального положення, розташованого на краю прямої дороги.
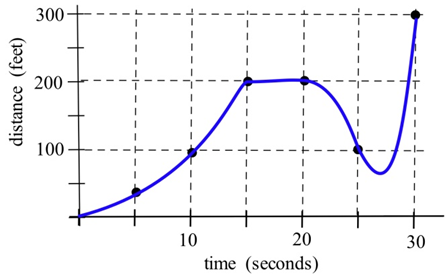
(а) Якою була середня швидкість руху автомобіля від\(t = 0\) до\(t = 30\) секунд?
(б) Якою була середня швидкість руху автомобіля від\(t = 10\) до\(t = 30\) секунд?
(c) Про те, наскільки швидко автомобіль подорожував за\(t = 10\) лічені секунди? в\(t = 20\) s? в\(t = 30\) s?
(d) Що означає горизонтальна частина графіка між секундами\(t = 15\) та\(t = 20\) секундами?
(e) Що\(t = 25\) являє собою негативна швидкість?
Графік показує відстань автомобіля від вимірювального положення, розташованого на краю прямої дороги.
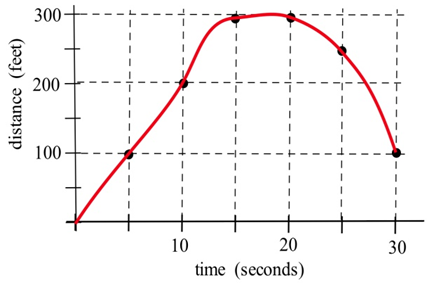
(а) Якою була середня швидкість руху автомобіля від\(t = 0\) до\(t = 20\) секунд?
(b) Якою була середня швидкість від\(t = 10\) до\(t = 30\) секунд?
(c) Про те, наскільки швидко автомобіль подорожував за\(t = 10\) лічені секунди? в\(t = 20\) s? в\(t = 30\) s?
На графіку показаний складний рівень розвитку майстерності шахістів у різному віці, що визначається їх виконанням проти інших шахістів. (З «Системи рейтингів людських здібностей», В.Х. Батчелдер та Р.С. Сімпсон, 1988. UMAP Модуль 698.)
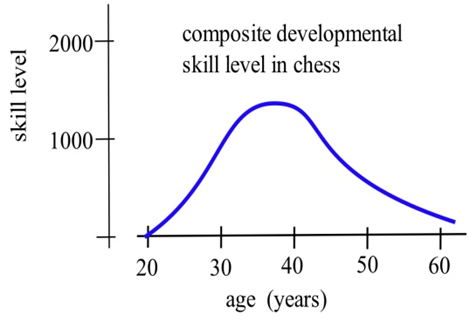
(а) В якому віці «типовий» шаховий майстер грає в найкращі шахи?
(б) Приблизно в якому віці рівень майстерності шахіста зростає найбільш швидко?
(c) Опишіть розвиток «типового» майстерності шахіста словами.
(d) Графіки ескізу, які, на вашу думку, розумно описують рівні продуктивності в порівнянні з віком для спортсмена, класичного піаніста, рок-співака, математика та професіонала у вашій основній галузі.
Використовуйте функцію на графіку, щоб заповнити таблицю, а потім графік\(m(x)\).
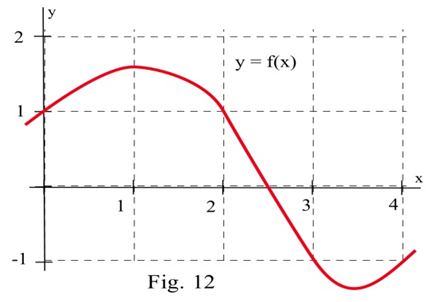
| \(x\) | \(y = f(x)\) | \(m(x) = \)розрахунковий нахил дотичної лінії до\(y=f(x)\) точки\((x,y)\) |
| 0 | ||
| 0.5 | ||
| 1.0 | ||
| 1.5 | ||
| 2.0 | ||
| 2.5 | ||
| 3.0 | ||
| 3.5 | ||
| 4.0 |
Використовуйте функцію на графіку, щоб заповнити таблицю, а потім графік\(m(x)\).
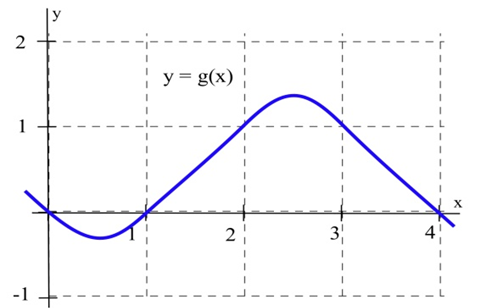
| \(x\) | \(y = g(x)\) | \(m(x) = \)розрахунковий нахил дотичної лінії до\(y=g(x)\) точки\((x,y)\) |
| 0 | ||
| 0.5 | ||
| 1.0 | ||
| 1.5 | ||
| 2.0 | ||
| 2.5 | ||
| 3.0 | ||
| 3.5 | ||
| 4.0 |
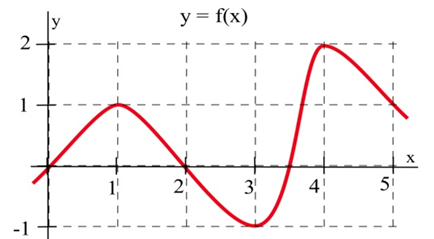
(а) При яких значеннях графіка\(x\)\(f\) на графіку має горизонтальну дотичну лінію?
(b) При якому значенні (-ах) значення\(f\) найбільшого?\(x\) найменший?
(c) Намалюйте графік\(m(x)\) = нахил прямої дотичної до графіка\(f\) в точці\((x,y)\)
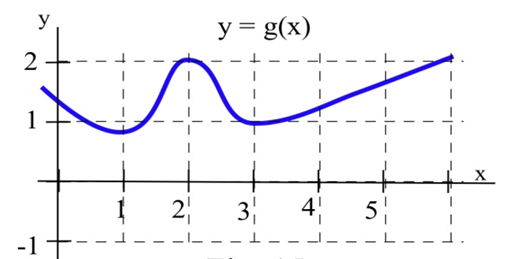
(а) При яких значеннях графа\(x\) має горизонтальну дотичну лінію?\(g\)
(b) При якому значенні (-ах) значення\(g\) найбільшого?\(x\) найменший?
(c) Намалюйте графік\(m(x) =\) нахилу прямої дотичної до графіка\(g\) в точці\((x,y)\).
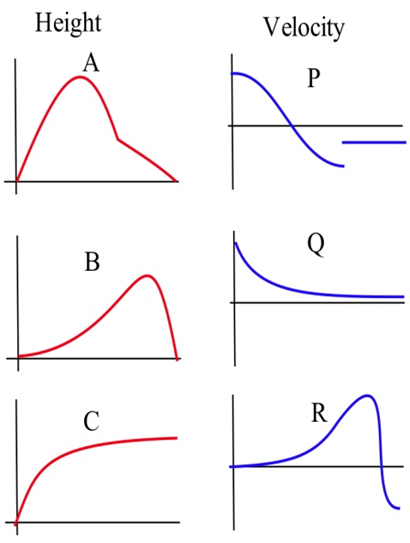
Зіставте описи ситуації з відповідним графіком часу та швидкості.
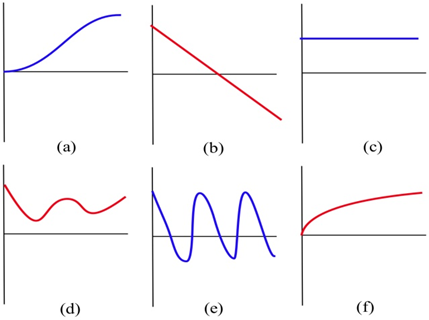
(а) Автомобіль швидко виїжджає зі знаку зупинки.
(б) Автомобіль седативно виїжджає від знака зупинки.
(c) Студент підстрибує на батуті.
(г) М'яч, кинутий прямо вгору.
(e) Студент впевнено крокує через кампус, щоб пройти тест на обчислення.
(f) Непідготовлений студент, що йде по кампусу, щоб пройти тест на обчислення.
Для кожної функції\(f(x)\) в задачах 14 — 19 виконайте кроки (а) — (d):
(а) обчислити\(m_{\sec} = \frac{f(x+h)-f(x)}{h}\) і спростити
(б) визначити\(m_{\tan} = \lim_{h \to 0} m_{\sec}\)
(c) оцінювати\(m_{\tan} \) при\(x = 2\),
(г) знайти рівняння прямої дотичної до графіка\(f\) at\((2, f(2) )\)
| 14. \(f(x) = 3x – 7\) | 15. \(f(x) = 2 – 7x\) | 16. \(f(x) = ax + b\)де\(a\) і\(b\) є константами |
| 17. \(f(x) = x^2 + 3x\) | 18. \(f(x) = 8 – 3x^2\) | 19. \(f(x) = ax^2 + bx + c\)де\(a\),\(b\) і\(c\) є константами |
Зіставте графіки трьох функцій нижче з графіками їх похідних.
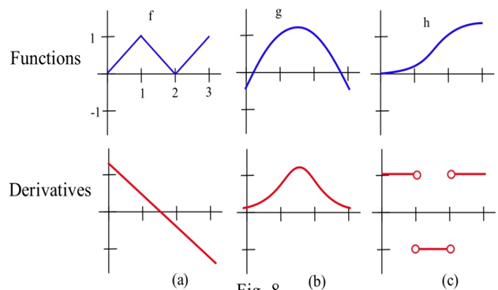
Нижче наведено шість графіків, три з яких є похідними від трьох інших. Зіставте функції з їх похідними.
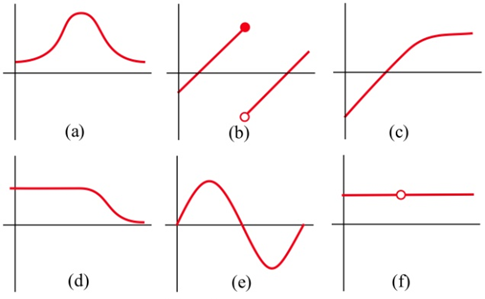
На графіку нижче показана температура протягом літнього дня в Чикаго. Намалюйте графік швидкості, з якою змінюється температура. (Це лише графік нахилів ліній, які є дотичними до температурного графіка.)
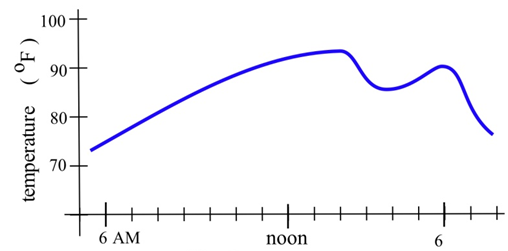
Заповніть таблицю відповідними одиницями для\(f '(x)\).
|
одиниць для\(x\) |
одиниць для\(f(x)\) |
одиниць для\(f '(x)\) |
|
годин |
миль |
|
|
людей |
автомобілі |
|
|
доларів |
млинці |
|
|
днів |
форель |
|
|
секунд |
миль в секунду |
|
|
секунд |
галони |
|
|
навчальні години |
контрольні точки |
\(C(x)\)Це загальна вартість, в мільйоні, виробництва\(x\) тисяч предметів, інтерпретувати\(C'(4) = 2\).
\(P(t)\)Припустимо, кількість особин, заражених хворобою через кілька\(t\) днів після його першого виявлення. Інтерпретувати\(P'(50) = -200\).
2.3 Вправи
Заповніть значення в таблиці для\(\frac{d}{dx} (3(f(x))\)\(\frac{d}{dx}(2f(x)+g(x))\), і\(\frac{d}{dx}(3(g(x)-f(x))\).
| \(x\) | \(f(x)\) | \(f'(x)\) | \(g(x)\) | \(g'(x)\) | \(\frac{d}{dx} (3(f(x))\) | \(\frac{d}{dx}(2f(x)+g(x))\) | \(\frac{d}{dx}(3(g(x)-f(x))\) |
| 0 | 3 | -2 | -4 | 3 | |||
| 1 | 2 | -1 | 1 | 0 | |||
| 2 | 4 | 2 | 3 | 1 |
Знайти
(а)\(D( x^{12} )\)
(б)\(\frac{d}{dx} (\sqrt[7]{x})\)
(c)\(D(\frac{1}{x^3})\)
(г)\(\frac{d x^e}{dx}\)
Знайти
(а)\(D( x^{9} )\)
(б)\(\frac{d x^{2/3}}{dx}\)
(c)\(D(\frac{1}{x^4})\)
(г)\(D(x^{\pi})\)
У задачах 4 — 8, (а) обчислити\(f '(1)\) і (б) визначити, коли\(f '(x) = 0\).
| 4. \(f(x) = x^2 – 5x + 13\) |
| 5. \(f(x) = 5x^2 – 40x + 73\) |
| 6. \(f(x) = x^3 + 9x^2 + 6\) |
| 7. \(f(x) = x^3 + 3x^2 + 3x – 1\) |
| 8. \(f(x) = x^3 + 2x^2 + 2x – 1\) |
Де роблять\(f(x) = x^2 – 10x + 3\) і\(g(x) = x^3 – 12x\) мають горизонтальні дотичні лінії?
Щоб сплести\(x\) невеликі килимки, потрібні\(T(x) = x^2\) години. Який граничний час виготовлення плести килимок? (Обов'язково включіть одиниці з вашою відповіддю.)
Це коштує\(C(x) = \sqrt{x}\) доларів, щоб виробляти х м'ячі для гольфу. Яка гранична вартість виробництва, щоб зробити м'яч для гольфу? Яка гранична собівартість виробництва, коли\(x = 25\)? коли\(x= 100\)? (Включити одиниці.)
Стрілка, знята прямо з рівня землі з початковою швидкістю 128 футів в секунду, буде на висоті\(h(x) = –16x^2 + 128x\) футів у\(x\) секундах.
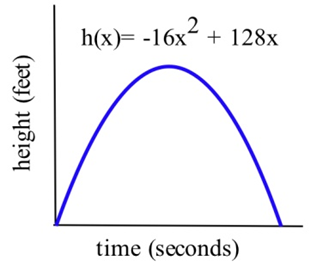
(а) Визначити швидкість стрілки, коли\(x =\) 0, 1 і 2 секунди.
(б) Яка швидкість стрілки\(v(x)\), в будь-який час\(x\)?
(c) В який час швидкість стрілки\(x\) буде дорівнює 0?
(d) Яку найбільшу висоту досягає стрілка?
(e) Як довго буде стрілка висотою?
(f) Використовуйте відповідь на швидкість у частині (b), щоб визначити прискорення\(a(x) = v '(x)\), у будь-який час\(x\).
Якщо стрілка вистрілюється прямо з рівня землі на Місяці з початковою швидкістю 128 футів в секунду, її висота становитиме\(h(x) = –2.65x^2 + 128x\) фути в\(x\) секундах. Виконайте частини (а) — (е) задачі 40, використовуючи це нове рівняння для\(h\).
\(f(x) = x^3 + A x^2 + B x + C\)з константами\(A\),\(B\) і\(C\). Чи можете ви знайти умови на константах\(A\),\(B\) і\(C\) які гарантують, що граф\(y = f(x)\) має дві різні «вершини»? (Тут «вершина» означає місце, де крива змінюється від збільшення до зменшення або від зменшення до збільшення.)
2.4 Вправи
Використовуйте значення в таблиці, щоб заповнити решту таблиці.
| \(x\) | \(f(x)\) | \(f'(x)\) | \(g(x)\) | \(g'(x)\) | \(\frac{d}{dx} (f(x) \cdot g(x))\) | \(\frac{d}{dx}\left(\frac{f(x)}{g(x)}\right)\) | \(\frac{d}{dx}\left(\frac{g(x)}{f(x)}\right)\) |
| 0 | 3 | -2 | -4 | 3 | |||
| 1 | 2 | -1 | 1 | 0 | |||
| 2 | 4 | 2 | 3 | 1 |
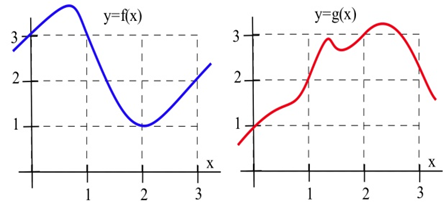
2. Використовуйте інформацію на графіку для побудови значень функцій\(f + g\)\(f \cdot g\)\(f/g\) та їх похідних у\(x =\) 1, 2 та 3.
3. Використовуйте інформацію на графіку для побудови значень функцій\(2f\)\(f – g\)\(g/f\) та їх похідних у\(x =\) 1, 2 та 3.
Обчисліть\(\frac{d}{dx} ((x-5)(3x+7))\) шляхом (а) за допомогою правила продукту і (б) розширення продукту, а потім диференціювання. Переконайтеся, що обидва методи дають однаковий результат.
Якщо твір\(f\) і\(g\) є постійним\(( f(x) \cdot g(x) = k\) для всіх\(x\)), то як\(\frac{\frac{d}{dx}(f(x))}{f(x)}\) і\(\frac{\frac{d}{dx}(g(x))}{g(x)}\) пов'язані?
Якщо частка\(f\) і\(g\) є постійною (\(\frac{f(x)}{g(x)} = k\)для всіх\(x\)), то як\(g \cdot f'\) і\(f \cdot g '\) пов'язані?
У задачах 7 — 8, (а) обчислити\(f '(1)\) і (б) визначити, коли\(f '(x) = 0\)
| 7. \(f(x) = \frac{7x}{x^2+4}\) | 8. \(f(x) = \frac{3x^2}{2x-3}\) |
Визначте\(\frac{d}{dx}(x^2 + 1)(7x - 3)\) і\(\frac{d}{dt}(\frac{3t-2}{5t+1})\).
Знайти (а)\(\frac{d}{dx}(x^3e^x)\) і (б)\(\frac{d}{dx}(e^x)^3\).
Знайти (а)\(\frac{d}{dt} (te^t)\), (б)\(d(e^x)^5\)
Виробник визначив, що працівник з d днів виробничого досвіду зможе виробляти приблизно одиниці\(P(d) = 3 + 15( 1 – e^{–0.2d} )\) продукції в день. Графік\(P(d)\).
(a) Приблизно скільки предметів може виробляти кожен день початківець працівник?
(b) Скільки предметів досвідчений працівник зможе виробляти щодня?
(c) Який граничний показник виробництва працівника з 5-денним стажем? (Які одиниці вашої відповіді, і що означає ця відповідь?
2.5 Вправи
Графік\(y = f(x)\) показаний.
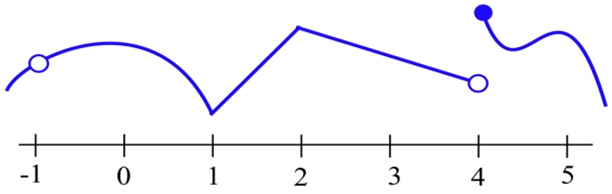
(a) У яких цілих чисел є\(f\) неперервними?
(b) У яких цілих чисел\(f\) диференційовні?
Графік\(y = g(x)\) показаний.
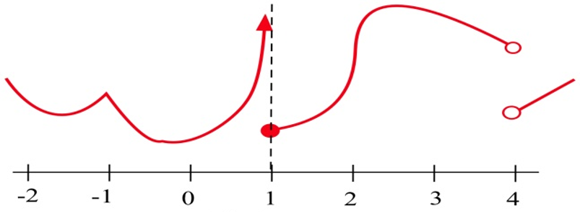
(a) У яких цілих чисел є\(g\) неперервними?
(b) У яких цілих чисел\(g\) диференційовні?
Проблеми 3 і 4 відносяться до значень, наведених в цій таблиці:
| \(x\) | \(f(x)\) | \(g(x)\) | \(f'(x)\) | \(g'(x)\) | \((f \circ g)(x)\) | \((f \circ g)' (x)\) |
| -2 | 2 | -1 | 1 | 1 | ||
| -1 | 1 | 2 | 0 | 2 | ||
| 0 | -2 | 1 | 2 | -1 | ||
| 1 | 0 | -2 | -1 | 2 | ||
| 2 | 1 | 0 | 1 | -1 |
3. Використовуйте таблицю значень для визначення\(( f \circ g )(x)\) і\(( f \circ g )' (x)\) в\(x =\) 1 і 2.
4. Використовуйте таблицю значень для визначення\(( f \circ g )(x)\) і\(( f \circ g )' (x)\) при\(x =\) —2, —1 і 0.
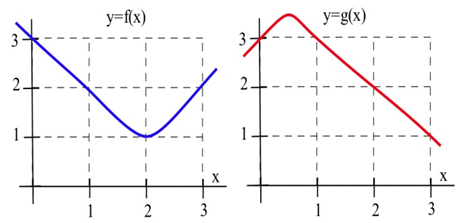
5. Використовуйте графіки для оцінки значень\(g(x)\),\(\bf g '(x)\),\((f \circ g)(x)\)\(\mathbf{f '(} g(x) \mathbf{)}\), і\(\mathbf{( f \circ g ) '(} x \mathbf{)}\) at\(x = 1\).
6. Використовуйте графіки для оцінки значень\(g(x)\),\(\bf g '(x)\),\((f \circ g)(x)\)\(\mathbf{f '(} g(x) \mathbf{)}\), і\(\mathbf{( f \circ g ) '(} x \mathbf{)}\) для\(x = 2\).
У задачах 7 — 12 знайти похідну від кожної функції.
| 7. \(f(x) = (2x – 8)^5\) | 8. \(f(x) = (6x – x^2)^{10}\) | 9. \(f(x) = x \cdot (3x + 7)^5\) |
| 10. \(f(x) = (2x + 3)^6 \cdot (x – 2)^4\) | 11. \(f(x) = \sqrt{x^2 + 6x - 1}\) | 12. \(f(x) = \frac{x-5}{(x+3)^4}\) |
Якщо\(f\) є диференційованою функцією,
(а) як складаються графіки\(y = f(x)\) та\(y = f(x) + k\) пов'язані?
(б) як похідні\(f(x)\) та\(f(x) + k\) пов'язані?
2.6 Вправи
У задачах 1 і 2 кожна цитата - це твердження про кількість чогось, що змінюється з плином часу. \(f(t)\)Дозволяти представляти кількість в той час\(t\). Для кожної цитати скажіть, що\(f\) являє собою і чи є перша та друга\(f\) похідні позитивними чи негативними.
1. (a) «Безробіття знову зросло, але темпи зростання менші, ніж минулого місяця».
(b) «Наш прибуток знову знизився, але повільнішими темпами, ніж минулого місяця».
(c) «Населення все ще зростає і швидшими темпами, ніж минулого року».
2. (а) «Температура у дитини все ще підвищується, але повільніше, ніж це було кілька годин тому».
(б) «Кількість китів зменшується, але повільнішими темпами, ніж минулого року».
(c) «Кількість людей з грипом зростає і швидше, ніж минулого місяця».
На яких інтервалах функція в графіку (а) увігнута вгору? (б) увігнуті вниз?
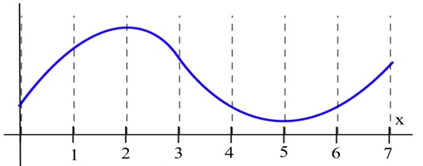
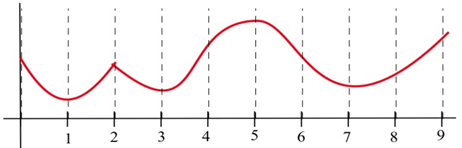
На яких інтервалах функція в графі (а) увігнута вгору? (б) увігнуті вниз?
Намалюйте графіки функцій, які визначені та увігнуті скрізь і які мають
(а) немає коренів.
(б) рівно 1 корінь.
(в) рівно 2 кореня.
(г) рівно 3 кореня.
У задачах 6 — 9 задано функцію та значення\(x\)\(f '(x) = 0\) so. Використовуйте другий тест похідних, щоб визначити, чи\((x, f(x))\) є кожна точка локальним максимумом, локальним мінімумом чи ні
| 6. \(f(x) = 2x^3 – 15x^2 + 6, x = 0, 5 \). |
| 7. \(g(x) = x^3 – 3x^2 – 9x + 7, x = –1, 3 \). |
| 8. \(h(x) = x^4 – 8x^2 – 2, x = –2, 0, 2 \). |
| 9. \(f(x) = x \cdot \ln(x), x = 1/e \). |
Які з позначених точок на графіку є точками перегину?
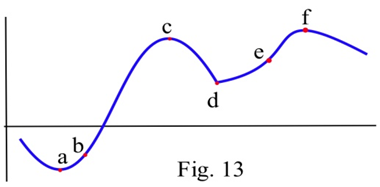
Які з позначених точок на графіку є точками перегину?
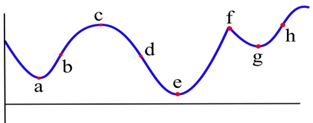
Скільки точок перегину може
(а) квадратичний многочлен мають?
(б) кубічний многочлен мають?
(c) поліном ступеня\(n\) мають?
Заповніть таблицю «+», «—» або «0" для показаної функції.
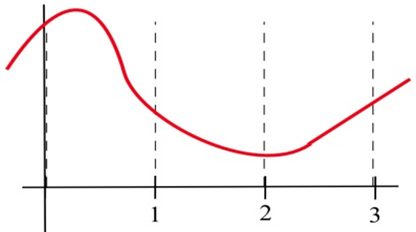
| \(x\) | \(f(x)\) | \(f'(x)\) | \(f''(x)\) |
| 0 | |||
| 1 | |||
| 2 | |||
| 3 |
Заповніть таблицю «+», «—» або «0" для показаної функції.
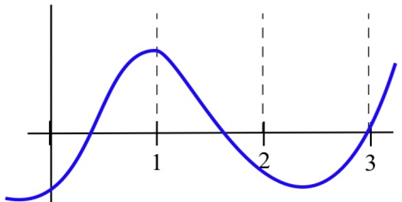
| \(x\) | \(g(x)\) | \(g'(x)\) | \(g''(x)\) |
| 0 | |||
| 1 | |||
| 2 | |||
| 3 |
У задачах 15 — 21 знайти похідну та другу похідну кожної функції.
| 15. \(f(x) = 7x^2 + 5x – 3\) |
| 16. \(f(x) = (2x – 8)^5\) |
| 17. \(f(x) = (6x – x^2)^{10}\) |
| 18. \(f(x) = x \cdot (3x + 7)^5 \) |
| 19. \(f(x) = (2x^3 + 3)^6\) |
| 20. \(f(x) = \sqrt{x^2 + 6x - 1}\) |
| 21. \(f(x) = \ln (x^2+4)\) |
2.7 Вправи
Знайдіть усі критичні точки показаної функції та ідентифікуйте їх як локальні max, локальні min або ні інші. Знайти глобальні max і min на інтервалі.
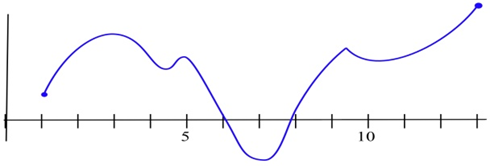
Знайдіть усі критичні точки показаної функції та ідентифікуйте їх як локальні max, локальні min або ні інші. Знайти глобальні max і min на інтервалі.
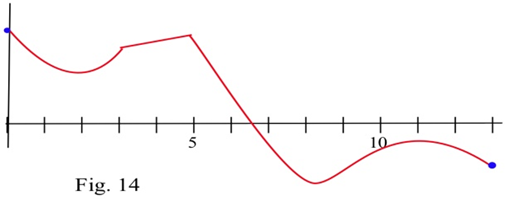
У задачах 3 — 8 знайти всі критичні точки та локальні максимуми та мінімуми кожної функції.
| 3. \(f(x) = x^2 + 8x + 7\) | 4. \(f(x) = 2x^2 – 12x + 7\) |
| 5. \(f(x) = x^3 – 6x^2 + 5\) | 6. \(f(x) = (x – 1)^2 (x – 3)\) |
| 7. \(f(x) = \ln ( x^2 – 6x + 11 )\) | 8. \(f(x) = 2x^3 – 96x + 42\) |
У задачах 9 — 16 знайти всі критичні точки та глобальні крайності кожної функції на заданих інтервалах.
| 9. \(f(x) = x^2 – 6x + 5\)на всій дійсному числовому рядку. |
| 10. \(f(x) = 2 – x^3\)на всій дійсному числовому рядку. |
| 11. \(f(x) = x^3 – 3x + 5\)на всій дійсному числовому рядку. |
| 12. \(f(x) = x - e^x\)на всій дійсному числовому рядку. |
| 13. \(f(x) = x^2 – 6x + 5\)на [—2, 5]. |
| 14. \(f(x) = 2 – x^3\)на [—2, 1]. |
| 15. \(f(x) = x^3 – 3x + 5\)на [—2, 1]. |
| 16. \(f(x) = x-e^x\)на [1, 2]. |
Припустимо\(f(1) = 5\), і\(f '(1) = 0\). Що можна зробити висновок про точку (1,5), якщо
(а)\(f '(x) < 0\) для\(x < 1\), і\(f '(x) > 0\) для\(x > 1\)?
(б)\(f '(x) < 0\) для\(x < 1\), а\(f '(x) < 0\) для\(x > 1\)?
(в)\(f '(x) > 0\) для\(x < 1\), і\(f '(x) < 0\) для\(x > 1\)?
(г)\(f '(x) > 0\) для\(x < 1\), і\(f '(x) > 0\) для\(x > 1\)?
\(A(x)\)Визначте область, обмежену між\(x\) віссю —, графіком\(f\) та вертикальною лінією\(x\).
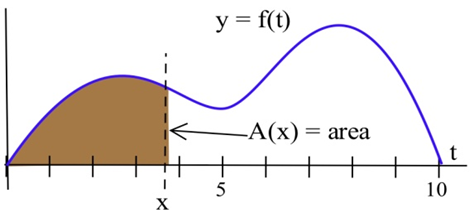
(а) При якому значенні\(x\) є\(A(x)\) мінімальним?
(б) При якому значенні\(x\) є\(A(x)\) максимальним?
\(S(x)\)Визначте нахил прямої через точки\((0,0)\) і на\(( x, f(x) )\) основі графіка\(f\) показаного.
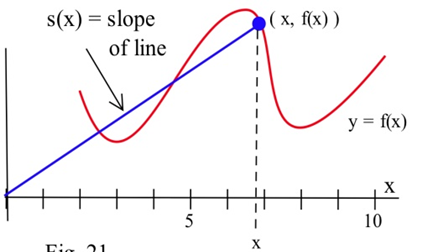
(а) При якому значенні\(x\) є\(S(x)\) мінімальним?
(б) При якому значенні\(x\) є\(S(x)\) максимальним?
Графік похідної неперервної функції\(f\).
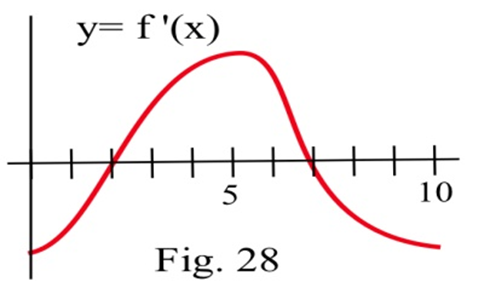
(a) Перерахуйте критичні числа\(f\).
(б) Для яких значень\(x\)\(f\) має локальний максимум?
(c) Для яких значень\(x\)\(f\) має локальний мінімум?
Графік похідної неперервної функції\(g\).
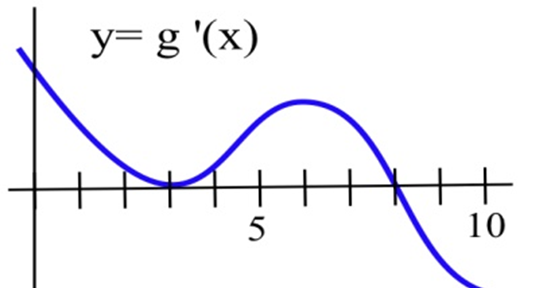
(a) Перерахуйте критичні числа\(g\).
(б) Для яких значень\(x\)\(g\) має локальний максимум?
(c) Для яких значень\(x\)\(g\) має локальний мінімум?
У задачах 22 — 24 задано функцію та значення\(x\)\(f '(x) = 0\) so. Використовуйте другий тест похідних, щоб визначити, чи\((x, f(x))\) є кожна точка локальним максимумом, локальним мінімумом чи ні
| 22. \(f(x) = 2x^3 – 15x^2 + 6, x = 0, 5 \). |
| 23. \(g(x) = x^3 – 3x^2 – 9x + 7, x = –1, 3\). |
| 24. \(h(x) = x^4 – 8x^2 – 2, x = –2, 0, 2 \). |
2.8 Вправи
Намалюйте графік безперервної функції\(f\) так, щоб
(a)\(f(1) = 3\)\(f '(1) = 0 \), і точка (1,3) є локальним максимумом\(f\).
(b)\(f(2) = 1\)\(f '(2) = 0 \), і точка (2,1) є локальним мінімумом\(f\).
(c)\(f(5) = 4\)\(f '(5) = 0\), і точка (5,4) не є локальним мінімумом або максимумом\(f\).
У задачах 2—4 намалюйте графік похідної кожної функції.
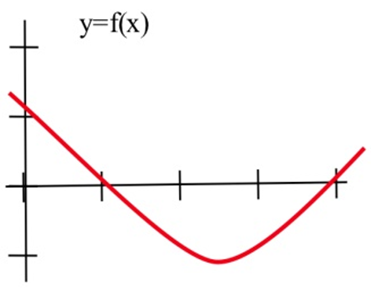
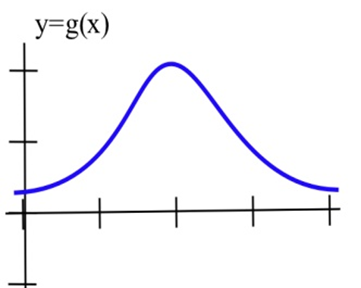
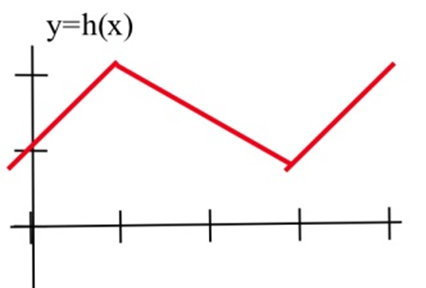
У задачах 5—7 показано графік висоти вертольота. Намалюйте графік висхідної швидкості вертольота.
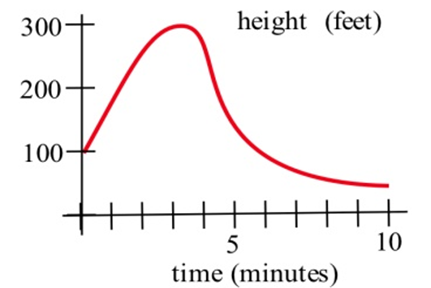
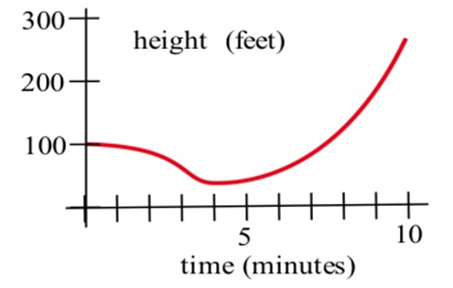
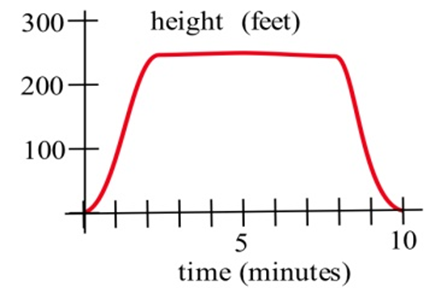
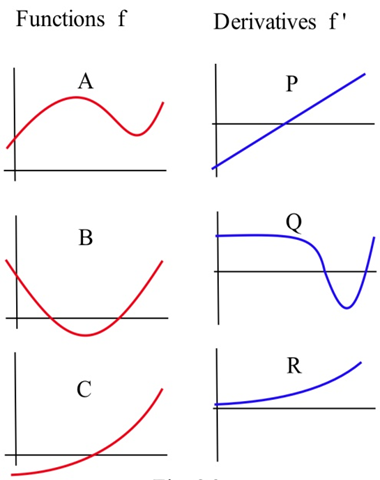
На графіках праворуч зіставте графіки функцій з графіками їх похідних
На графіках нижче зіставте графіки, що показують висоти ракет, з тими, що показують їх швидкості.
У задачах 10 — 14 використовуйте інформацію з похідних кожної функції, щоб допомогти вам скласти графік функції. Знайти всі локальні максимуми і мінімуми кожної функції.
| 10. \(f(x) = x^3 – 3x^2 – 9x – 5\) | 11. \(g(x) = 2x^3 – 15x^2 + 6\) | 12. \(h(x) = x^4 – 8x^2 + 3\) |
| 13. \(r(t) = \frac{2}{t^2+1}\) | 14. \(f(x) = \frac{x^2+3}{x}\) |
2.9 Вправи
(a) У вас є 200 футів огорожі доступні для побудови прямокутної ручки з парканом роздільник вниз по середині (див. Нижче). Які розміри пера укладають найбільшу загальну площу?
(б) Якщо вам потрібні 2 роздільники, які розміри пера охоплюють найбільшу площу?
(c) Які розміри в частинях (a) і (b), якщо один край пера межує з річкою і не вимагає жодних огорож?

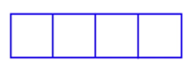
У вас є 120 футів огорожі, щоб побудувати ручку з 4 рівних розмірів кіосків. Якщо ручка прямокутна і має форму, подібну до наведеної нижче, які розміри пера найбільшої площі і що це за площа?
Припустимо, ви вирішили загородити прямокутний сад в кутку свого двору. Тоді дві сторони саду обмежені дворовим парканом, який вже є, тому вам потрібно використовувати лише 80 футів огорожі, щоб обкласти інші дві сторони. Які розміри нового саду найбільшої площі? Які розміри прямокутного саду найбільшої площі в кутку двору, якщо у вас є\(F\) ноги нового огорожі в наявності?
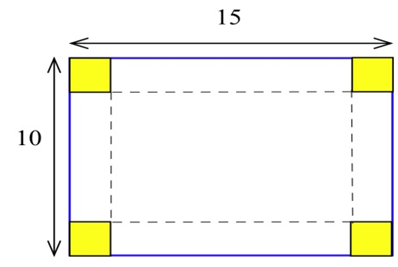
(а) У вас є шматок олова 10 дюймів на 15 дюймів, який ви плануєте сформувати в коробку (без верху), вирізавши квадрат з кожного кута і склавши з боків. Скільки потрібно відрізати від кожного кута, щоб вийшла коробка мала найбільший обсяг?
(b) Якщо шматок олова становить\(A\) дюйми на\(B\) дюйми, скільки ви повинні вирізати з кожного кута, щоб вийшла коробка мала найбільший обсяг?
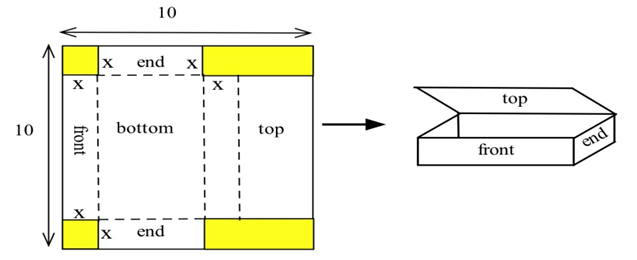
У вас є 10 дюймів на 10 дюймів шматок картону, який ви плануєте вирізати і скласти, як показано, щоб сформувати коробку з верхом. Знайдіть розміри коробки, яка має найбільший обсяг.
(а) Вас попросили зробити ставку на будівництво квадратного дна коробки без верхньої частини, яка буде містити 100 кубічних дюймів води. Якщо дно і бортики зроблені з одного матеріалу, які розміри короба, в якому використовується найменше матеріалу? (Припустимо, що жоден матеріал не витрачається даремно.)
(b) Припустимо, що коробка частково (а) використовує різні матеріали для дна та боків. Якщо нижній матеріал коштує 5 центів на квадратний дюйм, а бічний матеріал коштує 3¢ за квадратний дюйм, які розміри найменш дорогої коробки, яка вмістить 100 кубічних дюймів води?
(а) Визначте розміри найменш дорогої циліндричної банки, яка буде вміщати 100 кубічних дюймів, якщо матеріали коштують 2¢, 5¢ і 3¢ відповідно для верхньої, нижньої та бічних сторін.
(b) Як можуть змінитися розміри найменш дорогих, якщо нижній матеріал коштує більше 5 центів на квадратний дюйм?
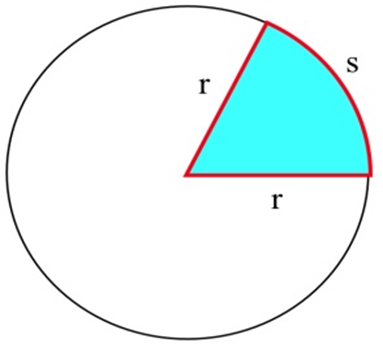
У вас є 100 футів огорожі, щоб побудувати перо у формі кругового сектора, показаний «шматочок пирога». Площа такого сектора є\((rs)/2\). Яке значення\(r\) максимізує закриту площу?
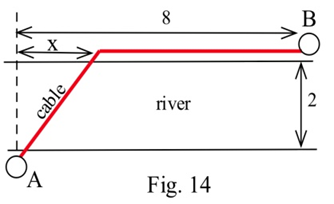
(a) Вас попросили визначити найменш дорогий маршрут для телефонного кабелю, який з'єднує Андерсонвілл з Beantown. Якщо це коштує 5000 доларів за милю, щоб прокласти кабель на суші та 8000 доларів за милю, щоб прокласти кабель через річку, а вартість кабелю незначна, знайдіть найменш дорогий маршрут.
(б) Який найменш дорогий маршрут, якщо кабель коштує 7000 доларів за милю плюс вартість його прокладки.
Вас попросили визначити, де водопровідні роботи повинні бути побудовані вздовж річки між Честервілл і Дентон, щоб мінімізувати загальну вартість труби до міст.
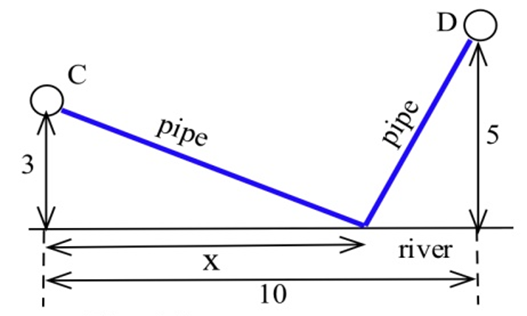
(а) Припустимо, що для кожного міста використовується однаковий розмір (і вартість) труби. (Цю частину можна зробити швидко, не використовуючи обчислення.)
(б) Припустимо, що труба до Честервілла коштує 3000 доларів за милю, а Дентон - 7000 доларів за милю.
Поштові правила США стверджують, що сума довжини та обхвату (відстані навколо) посилки повинна бути не більше 108 дюймів.
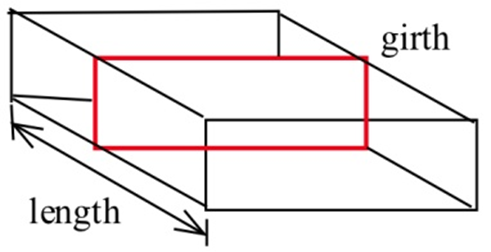
(а) Знайдіть розміри прийнятної коробки з квадратним кінцем, який має найбільший об'єм.
(b) Знайдіть розміри прийнятної коробки, яка має найбільший об'єм, якщо її кінець є прямокутником удвічі довшим за ширину.
(c) Знайдіть розміри прийнятної коробки з круглим кінцем, який має найбільший обсяг.
Сімонтон стверджує, що «рівні продуктивності» людей в різних сферах можна описати як функцію їх «кар'єрного віку»\(t\) тим,\(p(t) = e^{–at} – e^{ –bt}\) де\(a\) і\(b\) є константами, які залежать від сфери роботи, а кар'єрний вік приблизно на 20 менше фактичного віку індивідуальний.
(а) Виходячи з цієї моделі, в якому віці математики\((a=.03, b=.05)\), геологи\((a=.02, b=.04)\) та історики\((a=.02, b=.03)\) досягають максимальної продуктивності?
(б) Сімонтон каже: «За допомогою невеликого обчислення ми можемо показати, що крива\(( p(t) )\) максимізується»\(t = \frac{1}{b-a} \ln(\frac{b}{a})\). Використовуйте обчислення, щоб показати, що Сімонтон правильний.
Примітка: Моделі цього типу використовують для опису поведінки груп, але застосовувати описи груп або порівняння до осіб у групі небезпечно і зазвичай недійсним.
(Науковий геній, Дін Сімонтон, Кембриджська університетська преса, 1988, с. 69 — 73)
Ви володієте невеликим літаком, який вміщує максимум 20 пасажирів. Це коштує вам 100 доларів за рейс з Сент-Томаса до Сент-Круа за газ та заробітну плату плюс додаткові $6 на пасажира за додатковий газ, необхідний додатковою вагою. Плата за одного пасажира становить $30 кожен, якщо 10 чоловік чартер вашого літака (10 - це мінімальна кількість, яку ви будете літати), і цей збір зменшується на $1 за пасажира за кожного пасажира старше 10, який їде (тобто, якщо 11 їдуть, вони платять $29, якщо 12 їдуть вони кожен платить $28 і т.д.). Яка кількість пасажирів на рейсі дозволить максимізувати ваш прибуток?
При плануванні кав'ярні ми підраховуємо, що якщо є місця для розміщення від 40 до 80 осіб, щоденний прибуток становитиме 50 доларів за місце. Однак, якщо місткість місць перевищує 80 місць, щоденний прибуток на одне місце зменшиться на 1 долар за кожне додаткове місце понад 80. Якою має бути місткість сидіння, щоб максимізувати загальний прибуток кав'ярні?
При плануванні ресторану тако ми підрахували, що якщо є місця для розміщення від 10 до 40 осіб, щоденний прибуток становитиме 10 доларів за місце. Однак, якщо місткість місць більше 40 місць, щоденний прибуток на одне місце зменшиться на 0,20 долара за місце. Якою має бути місткість сидіння, щоб максимізувати загальний прибуток ресторану тако?
Загальна вартість в доларах для Алісії, щоб зробити\(q\) рукавиці для духовки, дається по\(C(q) = 64+1.5q+.01q^2\).
(а) Яка фіксована вартість?
(b) Знайдіть функцію, яка дає граничну вартість.
(c) Знайдіть функцію, яка дає середню вартість.
(d) Знайти кількість, яка мінімізує середню вартість.
(e) Підтвердьте, що середня вартість та гранична вартість дорівнюють вашій відповіді на частину (d).
Шакі робить і продає рюкзак бовтається. Загальна вартість в доларах для Шакі, щоб зробити\(q\) danglies дається\(C(q) = 75+2q+.015q^2\). Знайдіть кількість, яка мінімізує середню вартість Шакі на виготовлення зависання.
2.10 Вправи
Якщо\(g(20) = 35\) і\(g'(20)=-2\), оцініть вартість\(g(22)\).
Якщо\(g(1)=-17\) і\(g'(1)=5\), оцініть вартість\(g(1.2)\).
Використовуйте наближення дотичної лінії для оцінки кореня куба 9.
Використовуйте наближення дотичної лінії для оцінки п'ятого кореня з 30.
Прямокутник має одну сторону на\(x\) осі —, одну сторону на\(y\) осі —та кут на графіку\(y = x^2 + 1\).
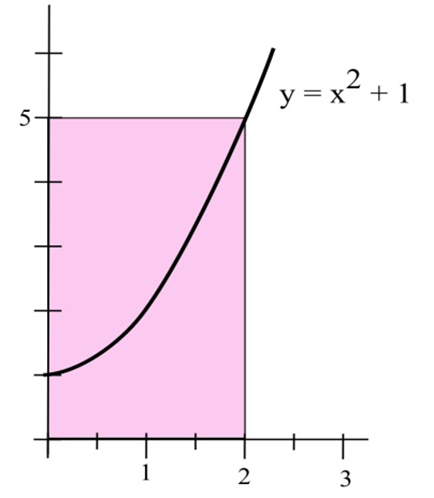
(a) Використовуйте лінійне наближення формули площі для оцінки збільшення площі прямокутника, якщо основа зростає від 2 до 2,3 дюймів.
(b) Обчисліть саме збільшення площі прямокутника, оскільки основа зростає від 2 до 2,3 дюйма.
Можна виміряти діаметр кола з точністю до 0,3 см.
(а) Наскільки велика «похибка» в розрахунковій площі кола з вимірюваним діаметром 7,4 см?
(б) Наскільки велика «похибка» в розрахунковій площі кола з вимірюваним діаметром 13,6 см?
(c) Наскільки велика процентна похибка в розрахунковій площі кола з вимірюваним діаметром\(d\)?
Функція попиту для духовки Алісії дається\(q=-8p+80\) (\(q\)це кількість рукавиць для духовки,\(p\) ціна в доларах). Знайти еластичність попиту, коли\(p =\) $7.50. Чи збільшиться дохід, якщо Алісія підніме ціну з $7,50?
Функція попиту для Shaki's danglies\(q\) задається\(q=-35p+205\) (це кількість зависань,\(p\) ціна в доларах за небезпеку). Знайти еластичність попиту, коли\(p =\) $5. Чи повинен Шакі підняти або знизити свою ціну, щоб збільшити дохід?
2.11 Вправи
У задачах 1 — 10 знаходять\(dy/dx\) шляхом диференціації неявно, потім знаходять значення\(dy/dx\) в заданій точці.
| 1. \(x^2 + y^2 = 100\), точка (6, 8) | 2. \(x^2 + 5y^2 = 45\), точка (5, 2) |
| 3. \(x^2 – 3xy + 7y = 5\), точка (2,1) | 4. \(\sqrt{x} + \sqrt{y} = 5\), точка (4,9) |
| 5. \(\frac{x^2}{9} + \frac{y^2}{16} = 1\), точка (0,4) | 6. \(\frac{x^2}{9} + \frac{y^2}{16} = 1\), точка (3,0) |
| 7. \(\ln(y) + 3x – 7 = 0\), точка (2,\(e\)) | 8. \(x^2 – y^2 = 16\), точка (5,3) |
| 9. \(x^2 – y^2 = 16\), точка (5, —3) | 10. \(y^2 + 7x^3 – 3x = 8\), точка (1,2) |
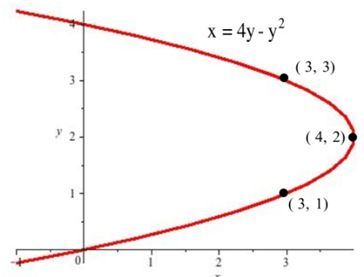
| 11. Знайдіть нахили ліній, дотичні до графіка, показаного в точках (3,1), (3,3) і (4,2). |
| 12. Знайдіть нахили ліній, дотичні до графіка на показаному місці, де графік перетинає\(y\) вісь —. |
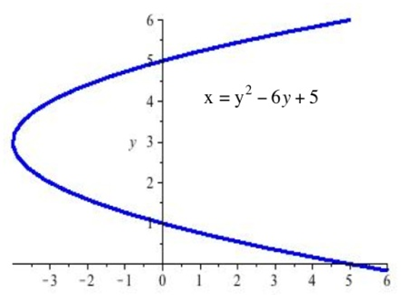
| 13. Знайдіть нахили ліній, дотичні до графіка на графіку, показаному в точках ((5,0), (5,6) і (—4,3). |
| 14. Знайдіть нахили ліній, дотичні до графіка на графіку, показаному там, де графік перетинає\(y\) вісь —. |
У задачах 15 — 16 знайти\(dy/dx\) за допомогою неявної диференціації, а потім знайти нахил прямої дотичної до графа рівняння в заданій точці.
| 15. \(y^3 – 5y = 5x^2 + 7\), точка (1,3) | 16. \(y^2 – 5xy + x^2 + 21 = 0\), точка (2,5) |
Розширюється сфера наповнюється рідиною з постійною швидкістю з крана (уявіть собі водяний балон, підключений до крана). Коли радіус сфери дорівнює 3 дюймам, радіус збільшується на 2 дюйми в хвилину. Як швидко рідина виходить з крана? \(( V = \frac{4}{3} \pi r^3 )\)
12-дюймова основа прямокутного трикутника зростає зі швидкістю 3 дюймів на годину, а висота 16 дюймів скорочується на 3 дюйми на годину.
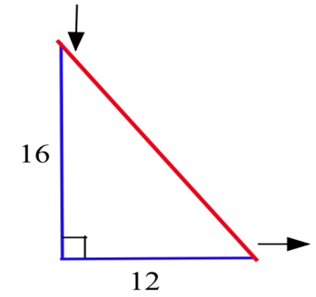
(а) Збільшується чи зменшується площа?
(b) Периметр збільшується або зменшується?
(c) Гіпотенуза збільшується або зменшується?
Через годину прямокутний трикутник у задачі 2 становить 15 дюймів у довжину і 13 дюймів у висоту, а основа та висота змінюються з тією ж швидкістю, що і в задачі 18.
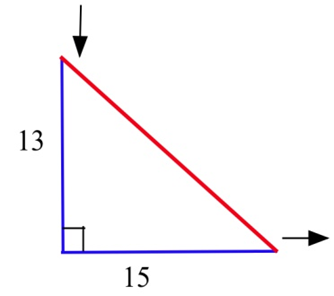
(а) Зараз площа збільшується чи зменшується?
(b) Гіпотенуза зростає або зменшується зараз?
(c) Чи збільшується чи зменшується периметр зараз?
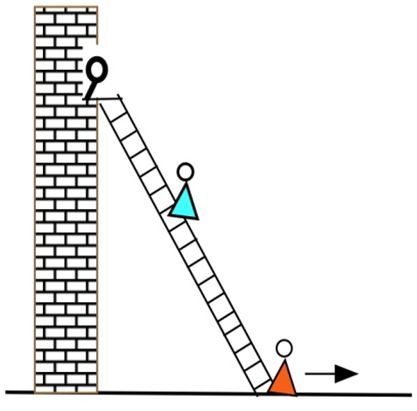
Молода жінка та її хлопець планують втекти, але вона повинна врятувати його від матері, яка замкнула його у своїй кімнаті. Молода жінка поставила драбину довжиною 20 футів проти свого будинку і стукає у його вікно, коли його мати починає відтягувати дно сходів від будинку зі швидкістю 3 фути в секунду. Як швидко падає верх сходів (і молода пара), коли внизу сходи
(а) 12 футів від нижньої частини стіни?
(б) 16 футів від нижньої частини стіни?
(c) 19 футів від нижньої частини стіни?
Довжина на 12 футів на 8 футів прямокутник збільшується зі швидкістю 3 футів в секунду, а ширина зменшується на 2 футів в секунду.
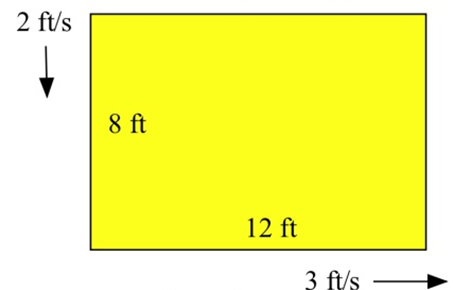
(a) Наскільки швидко змінюється периметр?
(б) Наскільки швидко змінюється площа?
Нафтовий танкер в Пьюджет Саунд виник витік, і утворюється кругова нафтова пляма. Масляна пляма має товщину 4 дюйми скрізь, становить 100 футів в діаметрі, а діаметр збільшується на 12 футів на годину. Ваше завдання, як командир берегової охорони або капітан танкера, полягає в тому, щоб визначити, наскільки швидко нафта витікає з танкера.
