2.7: Друга похідна і увігнутість
- Page ID
- 60373
Друга похідна і увігнутість
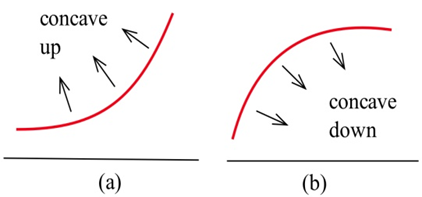
Графічно функція увігнута вгору, якщо її графік вигнутий з отвором вгору (рис.\(\PageIndex{1a}\)). Аналогічно функція увігнута вниз, якщо її графік відкривається вниз (рис.\(\PageIndex{1b}\)).
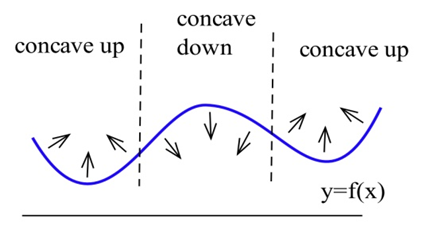
На цьому малюнку показана увігнутість функції в декількох точках. Зверніть увагу, що функція може бути увігнута вгору незалежно від того, збільшується вона або зменшується.
Наприклад, епідемія: Припустимо, почалася епідемія, і ви, як член конгресу, повинні вирішити, чи ефективні нинішні методи борються з поширенням хвороби чи потрібні більш рішучі заходи та більше грошей. На малюнку\(\PageIndex{2}\) нижче\(f(x)\) наведено кількість людей, які мають захворювання в той час\(x\), і показані дві різні ситуації. Як на малюнку\(\PageIndex{2b}\), так\(\PageIndex{2a}\) і на малюнку кількість людей з хворобою\(f(\text{now})\), і швидкість, з якою хворіють нові люди\(f'(\text{now})\), однакові. Різниця в двох ситуаціях полягає в увігнутості\(f\), і ця різниця в увігнутості може мати великий вплив на ваше рішення.
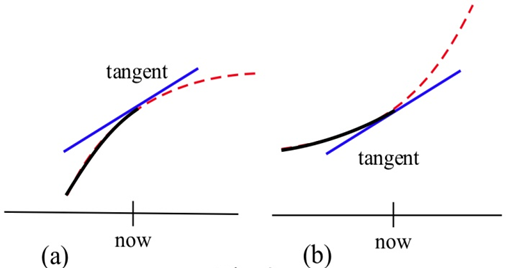
На малюнку\(\PageIndex{2a}\),\(f\) увігнута вниз на «зараз», схили зменшуються, і це виглядає так, ніби він хвостик. Можна сказати, що "\(f\)зростає зі зменшенням темпів». Схоже, що нинішні методи починають приводити епідемію під контроль.
На малюнку\(\PageIndex{2b}\),\(f\) увігнута вгору, нахили збільшуються, і це виглядає так, ніби він буде продовжувати збільшуватися все швидше і швидше. Схоже, епідемія все ще вийшла з-під контролю.
Відмінності між графіками походять від того, збільшується чи зменшується похідна.
Похідна функції\(f\) - це функція, яка дає інформацію про нахил\(f\). Похідна повідомляє нам, чи збільшується або зменшується вихідна функція.
Оскільки\(f'\) це функція, ми можемо взяти її похідну. Ця друга похідна також дає нам інформацію про нашу вихідну функцію\(f\). Друга похідна дає нам математичний спосіб визначити, як граф функції викривлений. Друга похідна повідомляє нам, чи є вихідна функція увігнутою вгору або вниз.
Нехай\( y=f(x) \). The друга похідна\(f\) - це похідна від\( y'=f'(x) \).
Використовуючи прості позначення, це\( f''(x) \) або\( y'' \). Ви можете прочитати це вголос як "\(f\)подвійне просте\(x\)» або «\(y\)подвійне просте».
За допомогою позначення Лейбніца записується друга похідна\( \frac{d^2y}{dx^2} \) або\( \frac{d^2f}{dx^2} \). Це читається вголос як «друга похідна\(y\) (або\(f\))».
Перша похідна повідомляє нам, чи збільшується чи зменшується функція
Якщо\( f'(x) \) позитивний на інтервалі, графік\( y=f(x) \) збільшується на цьому інтервалі.
Якщо\( f'(x) \) від'ємний на інтервалі, графік\( y=f(x) \) зменшується на цьому інтервалі.
Друга похідна говорить нам, якщо функція увігнута вгору або увігнута вниз.
Якщо\( f''(x) \) позитивний на інтервалі, графік\( y=f(x) \) увігнутий вгору на цьому інтервалі. Можна сказати, що\(f\) збільшується (або зменшується) зі зростаючою швидкістю.
Якщо\( f''(x) \) від'ємний на інтервалі, графік\( y=f(x) \) увігнутий вниз на цьому інтервалі. Можна сказати, що\(f\) відбувається збільшення (або зменшення) з убуваючою швидкістю.
Знайти\( f''(x) \) для\( f(x)=3x^7 \).
Для початку нам потрібно знайти першу похідну:\[f'(x)=21x^6.\nonumber \]
Тоді ми беремо похідну від цієї функції:\[f''(x)=\frac{d}{dx}\left( f'(x) \right)=\frac{d}{dx}\left( 21x^6 \right)=126x^5. \nonumber \]
Якщо\(f(x)\) представляє положення частинки в часі\(x\), то\(v(x) = f '(x)\) буде представляти швидкість (швидкість зміни положення) частинки і\(a(x) = v '(x) = f ''(x)\) представлятиме прискорення (швидкість зміни швидкості) частинки.
Ви напевно знайомі з прискоренням від водіння або їзди на автомобілі. Спідометр повідомляє вам вашу швидкість (швидкість). Коли ви йдете з зупинки і натискаєте на акселератор, ви прискорюєтеся - збільшуєте свою швидкість.
Висота (фути) частинки в\(t\) секундах часу дорівнює\(f(t) = t^3 – 4t^2 + 8t\). Знайти висоту, швидкість і прискорення частинки, коли\(t =\) 0, 1 і 2 секунди.
\(f(t) = t^3 – 4t^2 + 8t\)так\(f(0) = 0\) стопи,\(f(1) = 5\) стопи, і\(f(2) = 8\) стопи.
Швидкість\(v(t) = f '(t) = 3t^2 – 8t + 8\) така\( v(0) = 8\) ft/s,\(v(1) = 3\) ft/s і\(v(2) = 4\) ft/s. в кожен з цих часів швидкість позитивна, а частинка рухається вгору, збільшуючись у висоту.
Прискорення\(a(t) = f ''(t) = 6t – 8\) так\(a(0) = –8 \text{ ft/s\(^2\)}\),\(a(1) = –2 \text{ ft/s\(^2\)}\) і\(a(2) = 4 \text{ ft/s\(^2\)}\).
У момент 0 і 1 прискорення негативне, тому швидкість частинки зменшувалася б в цих точках - частка сповільнювалася. У момент 2 швидкість позитивна, тому частка збільшувалася в швидкості.
Точки перегину
Точка перегину - це точка на графіку функції, де змінюється увігнутість функції, від увігнутої вгору до вниз або від увігнутої вниз до верху.
Які з позначених точок на графіку нижче є точками перегину?
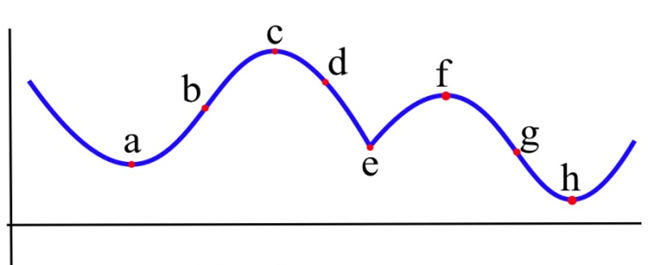
Увігнутість змінюється в точках b і g У точках a і h граф увігнутий вгору з обох сторін, тому увігнутість не змінюється. У точках c і f графік увігнутий вниз з обох сторін. У точці е, хоча графік виглядає дивно там, графік увігнутий вниз з обох сторін - увігнутість не змінюється.
Точки перегину трапляються при зміні увігнутості. Оскільки ми знаємо зв'язок між увігнутістю функції та знаком її другої похідної, ми можемо використовувати це, щоб знайти точки перегину.
Точка перегину - це точка на графіку, де друга похідна змінює знак.
Для того щоб друга похідна змінювала знаки, вона повинна бути або нульовою, або бути невизначеною. Таким чином, щоб знайти точки перегину функції нам потрібно тільки перевірити точки, де\(f ''(x)\) 0 або undefined.
Зауважте, що недостатньо, щоб друга похідна була нульовою або невизначеною. Нам ще потрібно перевірити, щоб знак\( f'' \) змін знаком. Функції в наступному прикладі ілюструють, що може статися.
Нехай\(f(x) = x^3\),\(g(x) = x^4\) і\(h(x) = x^{1/3}\). Для якої з цих функцій точка (0,0) точка перегину?
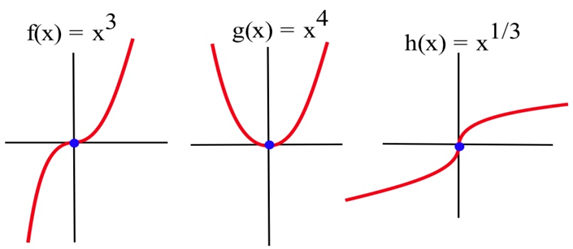
Графічно зрозуміло, що увігнутість\(f(x) = x^3\) і\(h(x) = x^{1/3}\) змінюється на (0,0), тому (0,0) є точкою перегину для\(f\) і\(h\). \(g(x) = x^4\)Функція увігнута всюди, тому (0,0) не є точкою перегину\(g\).
Ми також можемо обчислити другі похідні та перевірити зміну знака.
Якщо\(f(x) = x^3\), то\(f'(x) = 3x^2\) і\( f''(x) = 6x\). Єдина точка, в якій\(f''(x) = 0\) або є невизначеною (\(f'\)не диференційована) знаходиться в\(x = 0\). Якщо\( x \lt 0\), то\(f ''(x) \lt 0\)\(f\) так увігнута вниз. Якщо\(x \gt 0\), то\(f''(x) \gt 0\)\(f\) так увігнуто вгору. \(x = 0\)У увігнутості змінюється, тому точка\((0,f(0)) = (0,0)\) є точкою перегину\(f(x)=x^3\).
Якщо\(g(x) = x^4\), то\(g'(x) = 4x^3\) і\(g''(x) = 12x^2\). Єдина точка, в якій\(g''(x) = 0\) або не визначено, знаходиться в\(x = 0\). Якщо\(x \lt 0\), то\(g''(x) \gt 0\)\(g\) так увігнуто вгору. Якщо\(x \gt 0\), то\(g ''(x) \gt 0\) так\(g\) ще й увігнуті вгору. \(x = 0\)У увігнутості не змінюється, тому точка не\((0, g(0)) = (0,0)\) є точкою перегину\(g(x)=x^4\). Майте цей приклад на увазі!
Якщо\(h(x) = x^{1/3}\), то\(h'(x) = \frac{1}{3}x^{-2/3}\) і\(h''(x) = -\frac{2}{9}x^{-5/3}\). \(h''\)не визначено\(x = 0\), якщо, але\(h''(\text{negative number}) \gt 0\) і\(h''(\text{positive number}) \lt 0\) так\(h\) змінюється увігнутість при (0,0) і (0,0) є точкою перегину\(h\).
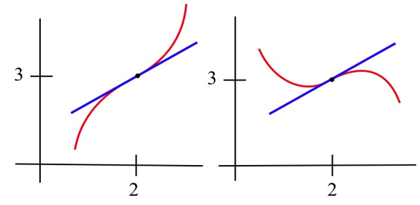
Намалюйте графік функції з\(f(2) = 3\) та точкою перегину в (2,3).\(f '(2) = 1\)
Тут показано два можливі рішення.