Skip to main content
LibreTexts - Ukrayinska

3.1: Визначення похідної

  1. Last updated
  2. Save as PDF
  • Page ID
    62275

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Цілі навчання
    • Розпізнайте значення дотичної до кривої в точці.
    • Обчисліть нахил дотичної лінії.
    • Визначте похідну як межу частки різниці.
    • Обчисліть похідну заданої функції в точці.
    • Опишіть швидкість як швидкість зміни.
    • Поясніть різницю між середньою швидкістю і миттєвою швидкістю.
    • Оцініть похідну з таблиці значень.

    Тепер, коли ми маємо як концептуальне розуміння межі, так і практичну здатність обчислювати межі, ми створили основу для нашого вивчення обчислення, галузі математики, в якій ми обчислюємо похідні та інтеграли. Більшість математиків і істориків сходяться на думці, що обчислення розроблялося самостійно англійцем Ісааком Ньютоном (1643—1727) і німецьким Готфрідом Лейбніцем (1646—1716), зображення якого фігурують на рисунку\(\PageIndex{1}\). Коли ми кредитуємо Ньютона і Лейбніца розвиваються числення, ми дійсно маємо на увазі той факт, що Ньютон і Лейбніц першими зрозуміли зв'язок між похідною і інтегралом. Обидва математики виграли від роботи попередників, таких як Барроу, Фермат і Кавальєрі. Початкові стосунки між двома математиками, схоже, були дружніми; однак у наступні роки спалахнула гірка суперечка щодо роботи яких мала пріоритет. Хоча здається ймовірним, що Ньютон дійсно прийшов до ідей, що стоять за обчисленням, ми зобов'язані Лейбніцу за позначення, які ми зазвичай використовуємо сьогодні.

    Фотографії Ньютона і Лейбніца.
    Малюнок\(\PageIndex{1}\): Ньютону і Лейбніцу приписують розвивається обчислення самостійно.

    дотичні лінії

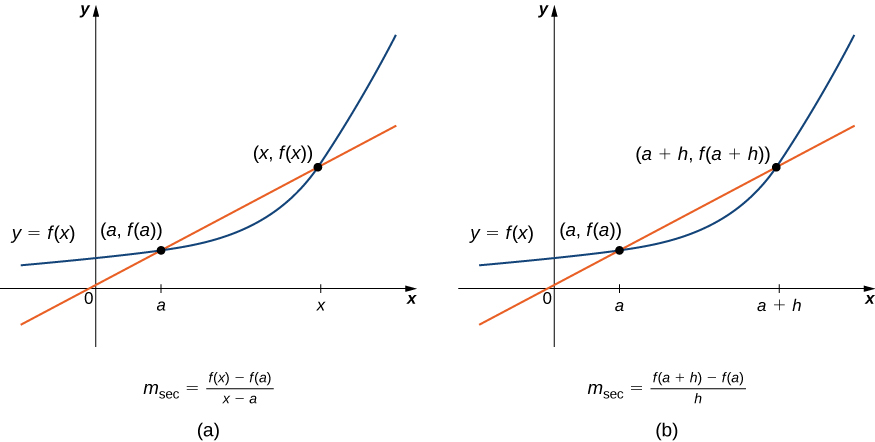
    Ми починаємо наше вивчення числення з перегляду поняття січних ліній і дотичних ліній. Нагадаємо, що ми використовували нахил січної лінії до функції в точці\((a,f(a))\) для оцінки швидкості зміни, або швидкості, з якою змінюється одна змінна по відношенню до іншої змінної. Ми можемо отримати нахил січної, вибравши значення x біля a і проведемо лінію через точки\((a,f(a))\) і\((x,f(x))\), як показано на малюнку\(\PageIndex{2}\). Нахил цієї лінії задається рівнянням у вигляді різницевого частки:

    \[m_{sec}=\frac{f(x)−f(a)}{x−a} \nonumber \]

    Ми також можемо обчислити нахил січної лінії до функції за значенням a, використовуючи це рівняння і замінивши\(x\) на\(a+h\), де\(h\) значення, близьке до a. Потім ми можемо обчислити нахил прямої через точки\((a,f(a))\) і\((a+h,f(a+h))\). У цьому випадку ми знаходимо, що січна лінія має нахил, заданий наступним різницевим часткою з приростом\(h\):

    \[m_{sec}=\frac{f(a+h)−f(a)}{a+h−a}=\frac{f(a+h)−f(a)}{h} \nonumber \]

    Визначення: Різниця коефіцієнта

    \(f\)Дозволяти функція, визначена на інтервалі,\(I\) що містить\(a\). Якщо\(x≠a\) є в\(I\), то

    \[Q=\frac{f(x)−f(a)}{x−a} \nonumber \]

    є часткою різниці.

    Крім того, якщо\(h≠0\) обраний так, що\(a+h\) є в\(I\), то

    \[Q=\frac{f(a+h)−f(a)}{h} \nonumber \]

    є різницевим коефіцієнтом з приростом\(h\).

    Ці два вирази для обчислення нахилу січної лінії проілюстровані на рисунку\(\PageIndex{2}\). Ми побачимо, що кожен з цих двох методів знаходження нахилу січної лінії має значення. Залежно від налаштування ми можемо вибрати те чи інше. Першочергове врахування в нашому виборі зазвичай залежить від простоти розрахунку.

    альт
    Малюнок\(\PageIndex{2}\): Ми можемо обчислити нахил січної лінії будь-яким з двох способів.

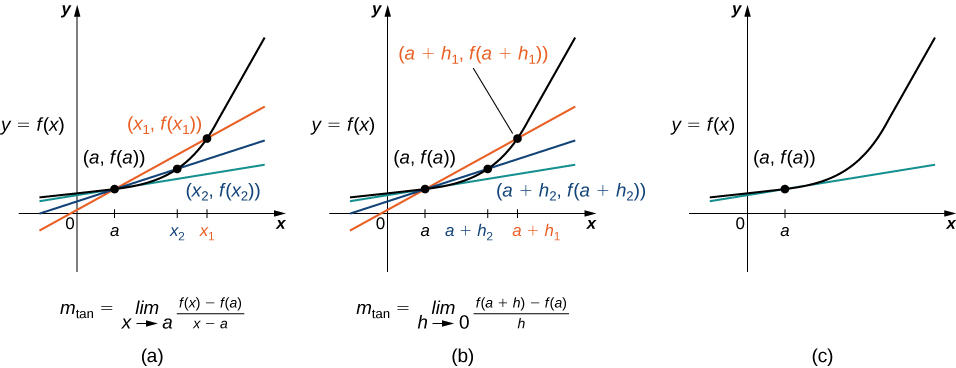
    На малюнку\(\PageIndex{3a}\) ми бачимо, що\(a\), як значення\(x\) наближення, нахили січних ліній забезпечують кращі оцінки швидкості зміни функції на\(a\). Крім того, січні лінії самі наближаються до дотичної лінії до функції at\(a\), яка представляє межу січних ліній. Аналогічно, Рисунок\(\PageIndex{3b}\) показує, що у міру\(h\) наближення\(0\) значень січні лінії також наближаються до дотичної лінії. Нахил дотичної лінії при\(a\) - це швидкість зміни функції на\(a\), як показано на малюнку\(\PageIndex{3c}\).

    Ця цифра складається з трьох графіків, позначених a, b і c. На малюнку a показана декартова координатна площина з 0, a, x2 та x1, позначені в порядку на осі x. Існує крива, позначена y = f (x) з позначеними точками (a, f (a)), (x2, f (x2)), і (x1, f (x1)). Є три прямі лінії: перші хрести (a, f (a)) і (x1, f (x1)); другі хрести (a, f (a)) і (x2, f (x2)); а третя стосується лише (a, f (a)), роблячи її дотичною. Внизу графіка задано рівняння mtan = limx → a (f (x) - f (a))/(x - a). На малюнку b показаний аналогічний графік, але цього разу a + h2 і a + h1 позначені на осі x замість x2 і x1. Отже, крива з міткою y = f (x) проходить через (a, f (a)), (a + h2, f (a + h2)), а (a + h1, f (a + h1)) і прямі аналогічно перетинають графік, як на малюнку а. внизу графіка рівняння mtan = limh → 0 (f (a + h) - f (a) /h дається. На малюнку c показана лише крива з міткою y = f (x) та її тангенс у точці (a, f (a)).
    Малюнок\(\PageIndex{3}\): Січні лінії наближаються до дотичної лінії (показано зеленим кольором), коли друга точка наближається до першої.

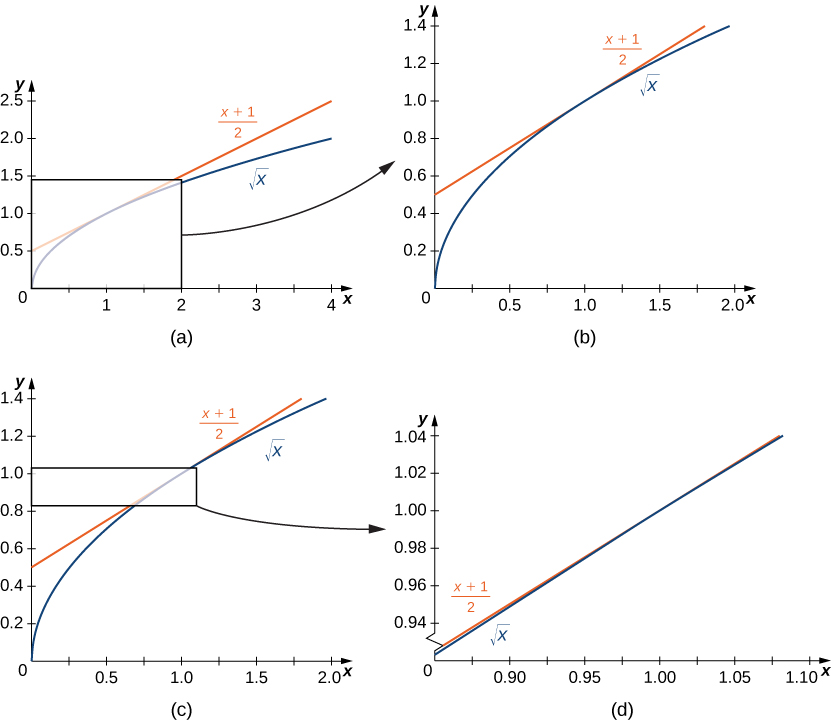
    На малюнку\(\PageIndex{4}\) ми показуємо графік\(f(x)=\sqrt{x}\) і його дотичну лінію\((1,1)\) в ряду більш жорстких інтервалів близько\(x=1\). У міру того, як інтервали стають більш вузькими, графік функції та її дотична лінія, здається, збігаються, що робить значення на дотичній лінії хорошим наближенням до значень функції для вибору\(x\) близького до\(1\). Фактично,\(f(x)\) сам графік, здається, локально лінійний в безпосередній близькості від\(x=1\).

    Ця цифра складається з чотирьох графіків, позначених a, b, c та d. на малюнку a показані графіки квадратного кореня x і рівняння y = (x + 1) /2 з віссю x, що йде від 0 до 4, а вісь y йде від 0 до 2,5. Графіки цих двох функцій виглядають дуже близько близько до 1; є поле навколо, де ці графіки виглядають близько. На малюнку b показано крупним планом цих самих двох функцій в області коробки з малюнка а, зокрема х, що йде від 0 до 2 і y, що йде від 0 до 1.4. Рисунок c - це той самий графік, що і на малюнку b, але цей має поле від 0 до 1.1 в координаті x та 0,8 та 1 на координаті y. Існує стрілка, яка вказує на те, що це підірвано на малюнку d Рисунок d показує дуже близьке зображення коробки з малюнка c, і дві функції, здається, торкаються майже по всій довжині графіка.
    Рисунок\(\PageIndex{4}\): Для значень\(x\) близьких до\(1\) графік\(f(x)=\sqrt{x}\) та його дотична лінія збігаються.

    Формально ми можемо визначити дотичну лінію до графіка функції наступним чином.

    Визначення: Дотична лінія

    \(f(x)\)Дозволяти функція, визначена у відкритому інтервалі, що містить\(a\). Дотична лінія до\(f(x)\) at\(a\) - це лінія, що проходить через точку,\((a,f(a))\) що має нахил.

    \[m_{tan}=\lim_{x→a}\frac{f(x)−f(a)}{x−a} \label{tanline1} \]

    за умови, що цей ліміт існує.

    Аналогічно, ми можемо визначити дотичну лінію до\(f(x)\) at,\(a\) щоб бути лінією, що проходить через точку,\((a,f(a))\) що має нахил

    \[m_{tan}=\lim_{h→0}\frac{f(a+h)−f(a)}{h} \label{tanline2} \]

    за умови, що цей ліміт існує.

    Так само, як ми використовували два різних вирази для визначення нахилу січної лінії, ми використовуємо дві різні форми для визначення нахилу дотичної лінії. У цьому тексті ми використовуємо обидві форми визначення. Як і раніше, вибір визначення буде залежати від настройки. Тепер, коли ми формально визначили дотичну лінію до функції в точці, ми можемо використовувати це визначення, щоб знайти рівняння дотичних ліній.

    Приклад\(\PageIndex{1}\): Finding a Tangent Line

    Знайти рівняння прямої дотичної до графіка\(f(x)=x^2\) at\(x=3.\)

    Рішення

    Спочатку знайдіть нахил дотичної лінії. У цьому прикладі використовуйте Equation\ ref {tanline1}.

    \ (\ displaystyle\ begin {align*} m_ {tan} &=\ lim_ {x→3}\ frac {f (x) −f (3)} {x−3} &\ text {Застосувати визначення.}\\ [4pt]
    &=\ lim_ {x→3}\ frac {x^2−9} {x−3} &\ text {Заміна} (x) =x^2\ текст {і} f (3) =9\\ [4pt]
    &=\ lim_ {x→3}\ розрив {(x−3) (x+3)} {x−3} =\ lim_ {x→3} (x+3) =6 & ; &\ text {Фактор чисельника для обчислення межі.} \ end {вирівнювати*}\)

    Далі знайдіть точку на дотичній лінії. Так як пряма дотична до графіка\(f(x)\) at\(x=3\), вона проходить через точку\((3,f(3))\). У нас є\(f(3)=9\), так дотична лінія проходить через точку\((3,9)\).

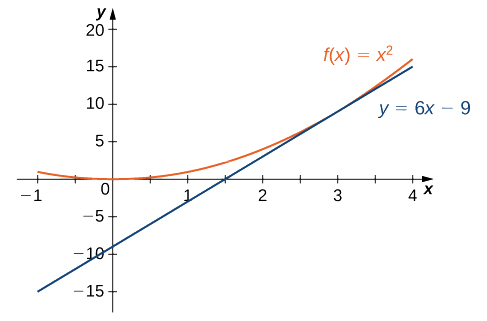
    Використовуючи точково-ухил рівняння лінії з нахилом\(m=6\) і точкою\((3,9)\), отримаємо пряму\(y−9=6(x−3)\). Спрощуючи, ми маємо\(y=6x−9\). Графік\(f(x)=x^2\) і його дотична лінія при\(3\) наведені на малюнку\(\PageIndex{5}\).

    Ця цифра складається з графіків f (x) = x в квадраті і y = 6х - 9. Графіки цих функцій, як видається, торкаються при x = 3.
    Малюнок\(\PageIndex{5}\): Дотична лінія до\(f(x)\) at\(x=3\).
    Приклад\(\PageIndex{2}\): The Slope of a Tangent Line Revisited

    Використовуйте Equation\ ref {tanline2}, щоб знайти нахил прямої дотичної до графа\(f(x)=x^2\) at\(x=3\).

    Рішення

    Кроки дуже схожі на приклад\(\PageIndex{1}\). Див. Рівняння\ ref {tanline2} для визначення.

    \ (\ begin {align*} m_ {tan} &=\ lim_ {h→0}\ frac {f (3+h) −f (3)} {h} &\ text {Застосувати визначення.}\\ [4pt]
    &=\ lim_ {h→0}\ frac {(3+h) ^2−9} {h} &\ text {Заміна} f (3+h) =( 3+год) ^2\ текст {і} f (3) =9\\ [4pt]
    &=\ lim_ {h → 0}\ frac {9+6h+h ^2−9} {h} &\ текст {Розгорнути і спростити оцінку межі.}\\ [4pt]
    &=\ lim_ {h→0}\ frac {h (6+h)} {h} =\ lim_ {h→0} (6+h) =6\ end {align*}\)

    Таке ж значення для нахилу дотичної лінії ми отримали за допомогою іншого визначення, демонструючи, що формули можна міняти місцями.

    Приклад\(\PageIndex{3}\): Finding the Equation of a Tangent Line

    Знайти рівняння прямої дотичної до графіка\(f(x)=1/x\) at\(x=2\).

    Рішення

    Ми можемо використовувати Equation\ ref {tanline1}, але, як ми бачили, результати однакові, якщо ми використовуємо Equation\ ref {tanline2}.

    \ (\ displaystyle\ begin {align*} m_ {tan} &=\ lim_ {x→2}\ frac {f (x) −f (2)} {x−2} &\ text {Застосувати визначення.}\\ [4pt]
    &=\ lim_ {x→2}\ гідророзриву {\ frac {1} {x}}} {x−2} &\ текст {Заміна} f (x) =\ frac {1} {x}\ текст {і} f (2) =\ frac {1} {2}\\ [4pt]
    &=\ lim_ {x→2}\ frac {\\ frac {1} {x} −\ frac {1} {2}} {x−2} ⋅\ frac {2x} {2x} &\ text {Помножте чисельник і знаменник на} 2x\ text {для спрощення дробів.}\\ [4pt]
    &=\ lim_ {x→2}\ frac {(2−x)} {x−2)} x)} &\ текст {Спрощення.}\\ [4pt]
    &=\ lim_ {x→2}\ frac {−1} {2x} &\ text {Спрощення використання}\ frac {2−x} {x−2} =−1,\ text {для} x2.\\ [4pt]
    &=−\ frac {1} {4} &\ text {Оцінити межу.} \ end {вирівнювати*}\)

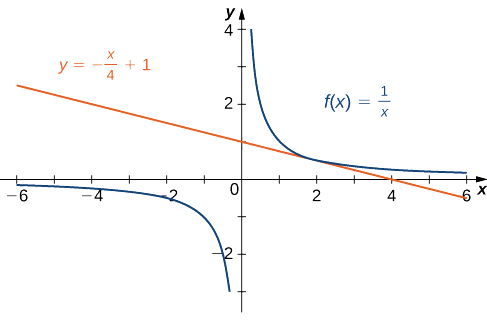
    Тепер ми знаємо, що нахил дотичної лінії є\(−\frac{1}{4}\). Щоб знайти рівняння дотичної прямої, нам також потрібна точка на прямій. Ми це знаємо\(f(2)=\frac{1}{2}\). Оскільки дотична лінія проходить через точку,\((2,\frac{1}{2})\) ми можемо використовувати рівняння точки-нахилу прямої, щоб знайти рівняння дотичної лінії. Таким чином, дотична лінія має рівняння\(y=−\frac{1}{4}x+1\). Графіки\(f(x)=\frac{1}{x}\) і\(y=−\frac{1}{4}x+1\) наведені на рис\(\PageIndex{6}\).

    Ця цифра складається з графіків f (x) = 1/x і y = -x/4 + 1. Здається, частина графіка f (x) = 1/x у першому квадранті торкається графіка іншої функції при x = 2.
    Малюнок:\(\PageIndex{6}\) Лінія дотична до at\(f(x)\).\(x=2\)
    Вправа\(\PageIndex{1}\)

    Знайти нахил прямої дотичної до графіка\(f(x)=\sqrt{x}\) at\(x=4\).

    Підказка

    Використовуйте або Рівняння\ ref {tanline1} або Рівняння\ ref {tanline2}. Помножте чисельник і знаменник на сполучений.

    Відповідь

    \(\frac{1}{4}\)

    Похідна функції в точці

    Тип межі, яку ми обчислюємо для того, щоб знайти нахил прямої дотичної до функції в точці, зустрічається у багатьох додатках у багатьох дисциплін. Ці програми включають швидкість та прискорення у фізиці, граничні функції прибутку в бізнесі та темпи зростання в біології. Ця межа зустрічається настільки часто, що ми даємо цьому значенню спеціальну назву: похідна. Процес знаходження похідної називається диференціацією.

    Визначення: Похідна

    \(f(x)\)Дозволяти функція, визначена у відкритому інтервалі, що містить\(a\). Похідна функції\(f(x)\) at\(a\), позначається\(f′(a)\), визначається

    \[f′(a)=\lim_{x→a}\frac{f(x)−f(a)}{x−a} \label{der1} \]

    за умови, що цей ліміт існує.

    Крім того, ми можемо також визначити похідну від\(f(x)\) at\(a\) як

    \[f′(a)=\lim_{h→0}\frac{f(a+h)−f(a)}{h}. \label{der2} \]

    Приклад\(\PageIndex{4}\): Estimating a Derivative

    Для\(f(x)=x^2\), скористайтеся таблицею для оцінки\(f′(3)\) за допомогою Equation\ ref {der1}.

    Рішення

    Створіть таблицю, використовуючи значення\(x\) трохи нижче\(3\) і трохи вище\(3\).

    \(x\) \(\dfrac{x^2−9}{x−3}\)
    \ (x\)» style="вирівнювання тексту: центр; "> 2.9 \ (\ dfrac {x^2−9} {x−3}\)» style="вирівнювання тексту: центр; ">5.9
    \ (x\)» style="вирівнювання тексту: центр; "> 2.99 \ (\ dfrac {x^2−9} {x−3}\)» style="вирівнювання тексту: центр; ">5.99
    \ (x\)» style="вирівнювання тексту: центр; "> 2.999 \ (\ dfrac {x^2−9} {x−3}\)» style="вирівнювання тексту: центр; ">5.999
    \ (x\)» style="вирівнювання тексту: центр; "> 3.001 \ (\ dfrac {x^2−9} {x−3}\)» style="вирівнювання тексту: центр; ">6.001
    \ (x\)» style="вирівнювання тексту: центр; "> 3.01 \ (\ dfrac {x^2−9} {x−3}\)» style="вирівнювання тексту: центр; ">6.01
    \ (x\)» style="вирівнювання тексту: центр; "> 3.1 \ (\ dfrac {x^2−9} {x−3}\)» style="вирівнювання тексту: центр; ">6.1

    Вивчивши таблицю, бачимо, що хороша оцінка є\(f′(3)=6\).

    Вправа\(\PageIndex{2}\)

    Для\(f(x)=x^2\), скористайтеся таблицею для оцінки\(f′(3)\) за допомогою Equation\ ref {der2}.

    Підказка

    Оцініть\(\dfrac{(x+h)^2−x^2}{h}\) на\(h=−0.1,\,−0.01,\,−0.001,\,0.001,\,0.01,\,0.1\)

    Відповідь

    6

    Приклад\(\PageIndex{6}\): Finding a Derivative

    Для\(f(x)=3x^2−4x+1\), знайдіть за\(f′(2)\) допомогою Рівняння\ ref {der1}.

    Рішення

    Підставляємо задану функцію і значення безпосередньо в рівняння.

    \ (\ стиль відображення\ почати {align*} f′ (x) &=\ lim_ {x→2}\ frac {f (x) −f (2)} {x−2} &\ text {Застосувати визначення.}\\ [4pt]
    &=\ lim_ {x→2}\ frac {(3x^2−4x+1) −5} {x−2} &\ текст {Заміна} f (x) =3x^2−4x+1\ текст {і} f (2) =5.\\ [4pt]
    &=\ lim_ {x→2}\ frac {(x−2) (3x+2)} {x−2} & & amp;\ text {Спрощення і множник чисельника.}\\ [4pt]
    &=\ lim_ {x→2} (3x+2) &\ text {Скасувати загальний коефіцієнт.}\\ [4pt]
    &=8 &\ text {Оцінити межу.} \ end {вирівнювати*}\)

    Приклад\(\PageIndex{7}\): Revisiting the Derivative

    Для\(f(x)=3x^2−4x+1\), знайдіть за\(f′(2)\) допомогою Рівняння\ ref {der2}.

    Рішення

    Використовуючи це рівняння, ми можемо підставити два значення функції в рівняння, і ми повинні отримати те саме значення, що і в прикладі\(\PageIndex{6}\).

    \ (\ стиль відображення\ почати {вирівнювати*} f′ (2) &=\ lim_ {h→0}\ frac {f (2+h) −f (2)} {h} &\ text {Застосувати визначення.}\\ [4pt]
    &=\ lim_ {h → 0}\ frac {(3 (2+h) ^2−4 (2+h) +1 5} {h} &\ текст {Заміна} f (2) =5\ текст {і} f (2+год) =3 (2+год) ^2−4 (2+год) +1.\\ [4pt]
    &=\ lim_ {h → 0}\ frac {3 (4+4h+h ^ 2) -8-4h+1-5} {h} &\ text {Розгорнути чисельник.}\\ [4pt]
    &=\ lim_ {h→0}\ frac {12+12h+3h^2-12-4h} {h} &\ text {Розподілити і почати спрощення чисельника.}\\ [4pt]
    &=\ lim_ {h → 0}\ frac {3pt h^2+8h} {h} &\ text {Завершити спрощення чисельника.}\\ [4pt]
    &=\ lim_ {h → 0}\ frac {h (3h+8)} {h} &\ text {Фактор чисельника.}\\ [4pt]
    &=\ lim_ {h→0} (3h+8) &\ text {Скасувати загальний фактор.}\\ [4pt] &=8 &\ text {Оцінити межу.}\\ [4pt] &=8 &\ text {Оцінити межу.}\\ [4pt]
    &=8 &\ text {Оцінити межу.} \ end {вирівнювати*}\)

    Результати однакові, чи ми використовуємо Equation\ ref {der1} або Equation\ ref {der2}.

    Вправа\(\PageIndex{4}\)

    Для\(f(x)=x^2+3x+2\), знайдіть\(f′(1)\).

    Підказка

    Використовуйте або Рівняння\ ref {der1}, Рівняння\ ref {der2}, або спробуйте обидва.

    Відповідь

    \(f′(1)=5\)

    Швидкість і швидкість зміни

    Тепер, коли ми можемо оцінити похідну, ми можемо використовувати її в додатках швидкості. Нагадаємо, що якщо\(s(t)\) це положення об'єкта, що рухається уздовж осі координат, то середня швидкість об'єкта за проміжок часу,\([a,t]\) якщо\(t>a\) або\([t,a]\) якщо\(t<a\) задана різницевим коефіцієнтом

    \[v_{ave}=\frac{s(t)−s(a)}{t−a}. \label{avgvel} \]

    Як значення\(t\) наближення\(a\), значення\(v_{ave}\) наближаються до значення, яке ми називаємо миттєвою швидкістю при\(a\). Тобто миттєва швидкість при\(a\), позначається\(v(a)\), задається

    \[v(a)=s′(a)=\lim_{t→a}\frac{s(t)−s(a)}{t−a}. \label{instvel} \]

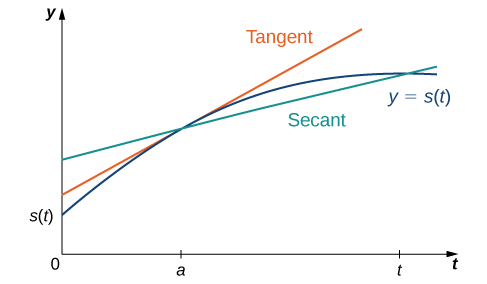
    Щоб краще зрозуміти взаємозв'язок між середньою швидкістю і миттєвою швидкістю, див\(\PageIndex{7}\). Рис. На цьому малюнку нахил дотичної лінії (показаний червоним кольором) - це миттєва швидкість об'єкта в момент, положення\(t=a\) якого в часі\(t\) задається функцією\(s(t)\). Нахил січної лінії (показаний зеленим кольором) - середня швидкість об'єкта за часовий проміжок\([a,t]\).

    Ця цифра складається з декартової координатної площини з позначками 0, a та t1 на осі t. Функція y = s (t) зображена в першому квадранті разом з двома лініями, позначеними дотичною та січною. Дотична лінія стосується y = s (t) лише в одній точці, (a, s (a)). Січна лінія стосується y = s (t) в двох точках: (a, s (a)) і (t1, s (t1)).
    Малюнок\(\PageIndex{7}\): Нахил січної лінії - середня швидкість за інтервал\([a,t]\). Нахил дотичної лінії - це миттєва швидкість.

    Ми можемо використовувати Equation\ ref {instvel} для обчислення миттєвої швидкості, або ми можемо оцінити швидкість рухомого об'єкта за допомогою таблиці значень. Потім ми можемо підтвердити оцінку за допомогою Equation\ ref {avgvel}.

    Приклад\(\PageIndex{8}\): Estimating Velocity

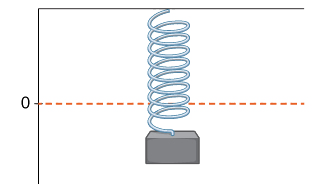
    Свинцева вага на пружині коливається вгору і вниз. Його положення в часі\(t\) по відношенню до нерухомої горизонтальної лінії задається\(s(t)=\sin t\) (рис.\(\PageIndex{8}\)). Використовуйте таблицю значень для оцінки\(v(0)\). Перевірте оцінку за допомогою Equation\ ref {instvel}.

    Зображення пружини, що звисає вниз з вагою в кінці. Існує горизонтальна пунктирна лінія, позначена 0 трохи вище ваги.
    Малюнок\(\PageIndex{8}\): Свинцева вага підвішена на пружині у вертикальному коливальному русі.

    Рішення

    Ми можемо оцінити миттєву швидкість при\(t=0\) обчисленні таблиці середніх швидкостей, використовуючи значення\(t\) наближення\(0\), як показано в табл\(\PageIndex{2}\).

    Таблиця\(\PageIndex{2}\): Середні швидкості з використанням значень\(t\) наближення 0
    \(t\) \(\frac{\sin t−\sin 0}{t−0}=\frac{\sin t}{t}\)
    \ (t\)» style="вирівнювання тексту: центр; ">−0.1 \ (\ frac {\ sin t−\ sin 0} {t−0} =\ frac {\ sin t} {t}\)» стиль ="вирівнювання тексту: центр; "> 0.998334166
    \ (t\)» style="вирівнювання тексту: центр; ">−0.01 \ (\ frac {\ sin t−\ sin 0} {t−0} =\ frac {\ sin t} {t}\)» стиль ="вирівнювання тексту: центр; "> 0.9999833333
    \ (t\)» style="вирівнювання тексту: центр; ">−0.001 \ (\ frac {\ sin t−\ sin 0} {t−0} =\ frac {\ sin t} {t}\)» стиль ="вирівнювання тексту: центр; ">0.999999833
    \ (t\)» style="вирівнювання тексту: центр; "> 0.001 \ (\ frac {\ sin t−\ sin 0} {t−0} =\ frac {\ sin t} {t}\)» стиль ="вирівнювання тексту: центр; ">0.999999833
    \ (t\)» style="вирівнювання тексту: центр; "> 0.01 \ (\ frac {\ sin t−\ sin 0} {t−0} =\ frac {\ sin t} {t}\)» стиль ="вирівнювання тексту: центр; "> 0.9999833333
    \ (t\)» style="вирівнювання тексту: центр; "> 0.1 \ (\ frac {\ sin t−\ sin 0} {t−0} =\ frac {\ sin t} {t}\)» стиль ="вирівнювання тексту: центр; "> 0.998334166

    З таблиці бачимо, що середня швидкість за часовий проміжок\([−0.1,0]\) дорівнює\(0.998334166\), середня швидкість за\([−0.01,0]\)\(0.9999833333\) часовий проміжок - і так далі. Використовуючи цю таблицю значень, виявляється, що хороша оцінка є\(v(0)=1\).

    Використовуючи рівняння\ ref {instvel}, ми бачимо, що

    \[v(0)=s′(0)=\lim_{t→0}\frac{\sin t−\sin 0}{t−0}=\lim_{t→0}\frac{\sin t}{t}=1. \nonumber \]

    Таким чином, власне,\(v(0)=1\).

    Вправа\(\PageIndex{5}\)

    Скеля скидається з висоти\(64\) ніг. Його висота над землею в часі\(t\) секунди пізніше задається\(s(t)=−16t^2+64,\;0≤t≤2\). Знайдіть його миттєву швидкість за\(1\) секунду після її скидання за допомогою Equation\ ref {instvel}.

    Підказка

    \(v(t)=s′(t)\). Дотримуйтесь попередніх прикладів похідної за допомогою Equation\ ref {instvel}.

    Відповідь

    −32 футів/с

    Як ми бачили в цьому розділі, нахил дотичної лінії до функції та миттєва швидкість є спорідненими поняттями. Кожен обчислюється шляхом обчислення похідної і кожен вимірює миттєву швидкість зміни функції, або швидкість зміни функції в будь-якій точці вздовж функції.

    Визначення: Миттєва швидкість зміни

    Миттєва швидкість зміни функції\(f(x)\) при значенні\(a\) є її похідною\(f′(a)\).

    Приклад\(\PageIndex{9}\): Chapter Opener: Estimating Rate of Change of Velocity

    Досягаючи максимальної швидкості\(270.49\) миль/год, Hennessey Venom GT є одним з найшвидших автомобілів у світі. У тестах він пішов від\(0\) до\(60\) миль/год за\(3.05\) лічені\(5.88\) секунди, від\(0\) до\(200\) миль/год за\(14.51\) секунди, від\(0\) до\(229.9\) миль/год за\(19.96\) секунди.\(0\)\(100\) Використовуйте ці дані, щоб зробити висновок про швидкість зміни швидкості (тобто її прискорення) при наближенні до\(229.9\) миль/год. Чи здається, що швидкість, з якою автомобіль розганяється, збільшується, зменшується або постійна?

    Той же спорткар, що розганяється по звивистій дорозі з початку глави.
    Малюнок\(\PageIndex{9}\): (Кредит: модифікація роботи по Codex41, Flickr)

    Рішення: Спочатку зауважте, що\(60\) mph =\(88\) ft/s,\(100\)\(200\) mph ≈\(146.67\)\(293.33\) ft/s, mph ≈\(337.19\) ft/s, і\(229.9\) mph ≈ ft/s Ми можемо узагальнити інформацію в таблиці.

    Таблиця\(\PageIndex{3}\): \(v(t)\) при різних значеннях\(t\)
    \(t\) \(v(t)\)
    \ (t\) ">0 \ (v (t)\) ">0
    \ (t\) ">3,05 \ (v (t)\) ">88
    \ (t\) ">5.88 \ (v (t)\) ">147.67
    \ (t\) ">14.51 \ (v (t)\) ">293.33
    \ (t\) ">19.96 \ (v (t)\) ">337.19

    Тепер обчислюємо середнє прискорення автомобіля в футах в секунду на інтервалах форми\([t,19.96]\) як\(t\) підходи\(19.96\), як показано в наступній таблиці.

    середнє прискорення
    \(t\) \(\dfrac{v(t)−v(19.96)}{t−19.96}=\dfrac{v(t)−337.19}{t−19.96}\)
    \ (t\) ">0.0 \ (\ dfrac {v (t) −v (19.96)} {t−19.96} =\ dfrac {v (t) −337.19} {t−19.96}\) ">16,89
    \ (t\) ">3,05 \ (\ dfrac {v (t) −v (19.96)} {t−19.96} =\ dfrac {v (t) −337.19} {t−19.96}\) ">14.74
    \ (t\) ">5.88 \ (\ dfrac {v (t) −v (19.96)} {t−19.96} =\ dfrac {v (t) −337.19} {t−19.96}\) ">13.46
    \ (t\) ">14.51 \ (\ dfrac {v (t) −v (19.96)} {t−19.96} =\ dfrac {v (t) −337.19} {t−19.96}\) ">8.05

    Швидкість, з якою автомобіль розганяється, зменшується, коли його швидкість наближається до\(229.9\) миль/год (\(337.19\)ft/s).

    Приклад\(\PageIndex{10}\): Rate of Change of Temperature

    Домовласник встановлює термостат так, що температура в будинку починає знижуватися з\(70°F\)\(9\) вечора, досягає мінімуму\(60°\) протягом ночі і піднімається назад до\(70°\) ранку наступного ранку.\(7\) Припустимо, що температура в будинку задана\(T(t)=0.4t^2−4t+70\) за\(0≤t≤10\), де\(t\) число годин минулих\(9\) п.м. знайти миттєву швидкість зміни температури опівночі.

    Рішення

    Оскільки опівночі - це\(3\) години минулої години\(9\) вечора, ми хочемо обчислити\(T′(3)\). Зверніться до Рівняння\ ref {der1}.

    \ (\ стиль відображення\ почати {вирівнювати*} T′ (3) &=\ lim_ {t→3}\ frac {T (t) −T (3)} {t−3} &\ text {Застосувати визначення.}\\ [4pt]
    &=\ lim_ {t→3}\ frac {0.4t^2−4t+70−61.6} {t−3} &\ текст {Заміна} T (t) =0.4t^2−4t+70\ текст {і} T (3) =61,6.\\ [4pt]
    &=\ lim_ {t→3}\ frac {0.4t^2−4t+8.4} {t− 3} &\ текст {Спрощення.}\\ [4pt]
    &=\ lim_ {t→3}\ frac {0.4 (t−3) (t−7)} {t−3}\\ [4pt]
    &=\ lim_ {t→3} 0,4 (t−7) &\ text {Скасувати.}\\ [4pt]
    &=−1.6 &\ text {Оцінити ліміт.} \ end {вирівнювати*}\)

    Миттєва швидкість зміни температури опівночі становить\(−1.6°F\) за годину.

    Приклад\(\PageIndex{11}\): Rate of Change of Profit

    Іграшкова компанія може продавати\(x\) електронні ігрові системи за ціною\(p=−0.01x+400\) доларів за ігрову систему. Вартість виготовлення\(x\) систем дається\(C(x)=100x+10,000\) доларами. Знайти швидкість зміни прибутку, коли виробляються\(10,000\) ігри. Чи повинна компанія іграшок збільшувати або зменшувати виробництво?

    Рішення

    Прибуток,\(P(x)\) отриманий при виробництві\(x\) ігрових систем\(R(x)−C(x)\),\(R(x)\) становить, де знаходиться дохід, отриманий від продажу\(x\) ігор. Оскільки компанія може продавати\(x\) ігри за\(p=−0.01x+400\) одну гру,

    \(R(x)=xp=x(−0.01x+400)=−0.01x^2+400x\).

    Отже,

    \(P(x)=−0.01x^2+300x−10,000\).

    Тому оцінка темпів зміни прибутку дає

    \ (\ стиль відображення\ почати {вирівнювати*} P′ (10000) &=\ lim_ {x → 10000}\ розрив {P (x) −P (10000)} {x−10000}\ [4pt]
    &=\ lim_ {x→10000}\ frac {−0.01x^2+300x−10000−1990000} {x−10000}\ [4pt]
    \ lim_ {x→10000}\ розрив {−0.01x^2+300x−2000000} {x−10000}\ [4pt]
    &=100\ кінець {вирівнювати*}\).

    Так як темпи зміни прибутку\(P′(10,000)>0\) і\(P(10,000)>0\), компанія повинна нарощувати виробництво.

    Вправа\(\PageIndex{6}\)

    Кав'ярня визначає, що щоденний прибуток від булочок, отриманий шляхом стягнення доларів за булочку, становить\(P(s)=−20s^2+150s−10\). Кав'ярня в даний час стягує плату\($3.25\) за сконе. Знайдіть\(P′(3.25)\), швидкість зміни прибутку, коли ціна є,\($3.25\) і вирішити, чи варто кав'ярні розглянути питання про підвищення або зниження цін на булочки.

    Підказка

    Використовуйте приклад\(\PageIndex{11}\) для керівництва.

    Відповідь

    \(P′(3.25)=20>0\); підвищувати ціни

    Ключові поняття

    • Нахил дотичної лінії до кривої вимірює миттєву швидкість зміни кривої. Ми можемо обчислити його, знайшовши межу коефіцієнта різниці або коефіцієнт різниці з приростом\(h\).
    • Похідна функції\(f(x)\) за\(a\) значенням знайдено за допомогою будь-якого з визначень нахилу дотичної прямої.
    • Швидкість - це швидкість зміни положення. Таким чином, швидкість\(v(t)\) в часі\(t\) є похідною від позиції\(s(t)\) в часі\(t\).
      Середня швидкість задається\[v_{ave}=\dfrac{s(t)−s(a)}{t−a}. \nonumber \] Миттєвою швидкістю задається\[\displaystyle v(a)=s′(a)=\lim_{t→a}\frac{s(t)−s(a)}{t−a}. \nonumber \]
    • Ми можемо оцінити похідну за допомогою таблиці значень.

    Ключові рівняння

    • Частота різниці

    \(Q=\dfrac{f(x)−f(a)}{x−a}\)

    • Частота різниці з приростом h

    \(Q=\dfrac{f(a+h)−f(a)}{a+h−a}=\dfrac{f(a+h)−f(a)}{h}\)

    • Нахил дотичної лінії

    \(\displaystyle m_{tan}=\lim_{x→a}\frac{f(x)−f(a)}{x−a}\)

    \(\displaystyle m_{tan}=\lim_{h→0}\frac{f(a+h)−f(a)}{h}\)

    • Похідна f (x) при a

    \(\displaystyle f′(a)=\lim_{x→a}\frac{f(x)−f(a)}{x−a}\)

    \(\displaystyle f′(a)=\lim_{h→0}\frac{f(a+h)−f(a)}{h}\)

    • Середня швидкість

    \(v_{ave}=\dfrac{s(t)−s(a)}{t−a}\)

    • Миттєва швидкість

    \(\displaystyle v(a)=s′(a)=\lim_{t→a}\frac{s(t)−s(a)}{t−a}\)

    Глосарій

    похідний
    нахил дотичної прямої до функції в точці, обчислюється шляхом взяття межі різницевого частки, є похідною
    коефіцієнт різниці

    функції\(f(x)\) at\(a\) задається

    \(\dfrac{f(a+h)−f(a)}{h}\)або\(\dfrac{f(x)−f(a)}{x−a}\)

    диференціація
    процес взяття похідної
    миттєва швидкість зміни
    швидкість зміни функції в будь-якій точці вздовж функції\(a\), яку також називають\(f′(a)\), або похідна функції при\(a\)