7.2: Абсолютна проти локальної екстреми
- Page ID
- 54329
Можливість ідентифікувати найменші та найбільші значення функції (екстреми), і де вони відбуваються в певному інтервалі в області або по всій області, корисно для побудови графіків рівняння функції, а також при вирішенні задач «оптимізації». Розташування цих крайнощів прив'язане до поведінки похідної. Ви дізналися в попередній роботі з квадратичними функціями (параболи,\( y=ax^2+bx+c \nonumber\)), що найменше або найбільше значення параболи можна знайти у вершині параболи (на осі симетрії\( x=− \frac{b}{2a} \nonumber\)). Як\( x=− \frac{b}{2a} \nonumber\) пов'язані похідні квадратичної функції і вершини?
Екстрема
Почнемо нашу дискусію з деяких формальних робочих визначень максимального та мінімального значень функції.
- Функція f має максимум у x = a, якщо\( f(a)≥f(x) \nonumber\) для всіх x у області f.
- Функція f має мінімум x = a, якщо\( f(a)≤f(x) \nonumber\) для всіх x у області f.
Значення функції для цих x-значень називаються екстремальними значеннями або екстремумами.
Ось приклад функції, яка має максимум у x = a і мінімум у x = d:
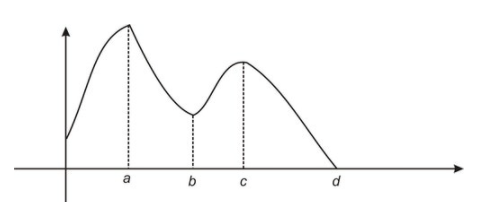
CC ЗА NC-SA
Спостерігайте за графом у x=b. Хоча у нас немає мінімуму x = b, ми зауважимо, що f (b) ≤f (x) для всіх x поблизу b. Ми говоримо, що функція має локальний мінімум у x=b.
Аналогічно, ми говоримо, що функція має локальний максимум при x = c, оскільки f (c) ≥f (x) для деяких х, що містяться у відкритих інтервалах c.
Не забудьте використовувати терміни максимум і мінімум (без включення терміна локальний) тільки тоді, коли ви говорите про абсолютні або глобальні екстремальні значення функції; локальні екстреми або відносні екстреми повинні називатися локальним максимумом або локальним мінімумом.
Чи всі функції мають максимум і мінімум? Так, всі безперервні функції роблять. Про це говорить теорема про екстремальні значення, яку ми обговорювали в концепції безперервності.
Теорема про екстремальні значення: Якщо функція f (x) є неперервною в замкнутому інтервалі I, то f (x) має як максимальне значення, так і мінімальне значення в I.
Це має сенс концептуально. Спробуйте намалювати функцію (на замкнутому інтервалі, включаючи кінцеві точки) так, щоб жодна точка не була в найвищій частині графіка. Незалежно від того, як намальована функція, буде принаймні одна точка, яка є найвищою.
Як екстремальні значення, максимуми і мінімуми, відносяться до похідних? Французький математик Ферма показує, як у теоремі Ферма: Якщо f (c) є екстремальним значенням f для деякого відкритого інтервалу, що містить c, то або f′ (c) =0, або f′ (c) не існує.
Ця залежність між розташуванням крайності і похідною в місці настільки важлива, що ми даємо розташуванню назву критичної точки.
Ми будемо називати x=c критичною точкою в замкнутому інтервалі [a, b], якщо f (c) існує, і або f′ (c) =0 або f′ (c) не існує.
Резюме поки що: Якщо функція є неперервною в замкнутому інтервалі, вона має як мінімум, так і максимум в деяких місцях, а похідна в цих місцях дорівнює або 0, або не існує. Локації називаються критичними точками.
На наведеній нижче схемі чітко визначено, як визначити критичні точки. Кінцеві точки замкнутого інтервалу включаються як критичні точки, якщо розглядати функцію, визначену тільки на замкнутому інтервалі, а не поза інтервалом. У цьому випадку похідна в кожній кінцевій точці не буде визначена.
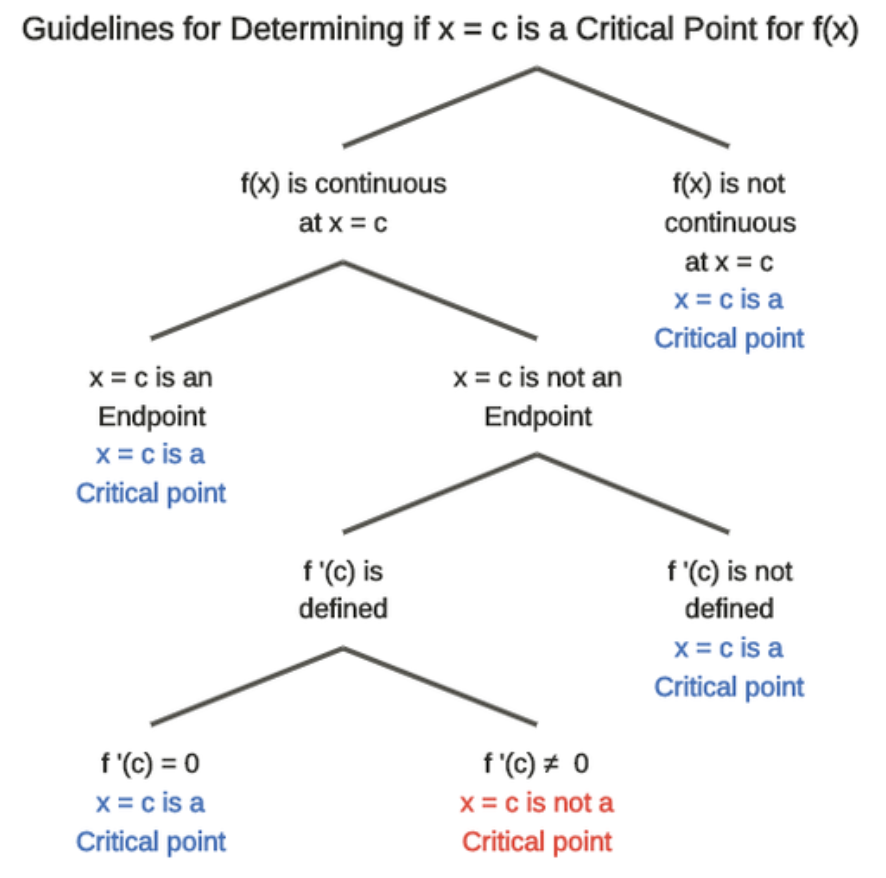
Деревоподібна діаграма, яка допоможе визначити критичні точки. Фонд СК-12
Розглянемо дві функції, показані нижче, і скажемо щось про них в замкнутому інтервалі [-2, 2]. Зверніть увагу, що g (x) (друга функція) має cusp при x = 0.
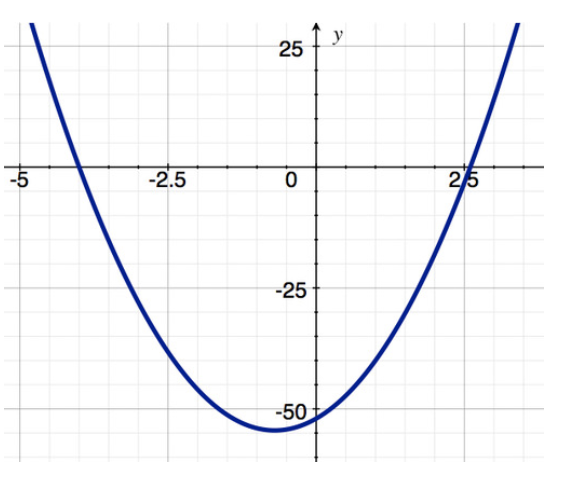
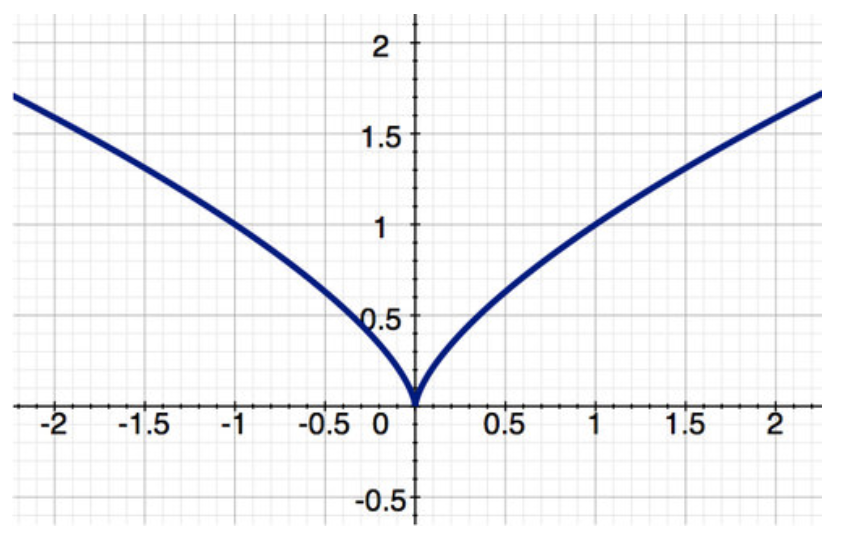
Дві функції
Обидві функції є неперервними в [-2, 2]. За теоремою крайніх значень вони обидва мають мінімум і максимум. Як видно з таблиці, f (x) має крайнє значення, де f′ (x) =0, а g (x) має крайнє значення, де g′ (x) не визначено. Це критичні моменти.
| Властивість функції | \( f(x)=5x^2+7x−52 \nonumber\) | \( g(x)=x^{\frac{2}{3}} \nonumber\) |
| Значення в кінцевій точці x = −2 | -46 | 1.59 |
| Значення в кінцевій точці x = 2 | -18 | 1.59 |
| Розташування та значення, де f′ (x) =0 | (-0.7, -54.45) | — |
| Місце, де f′ (x) не існує | Кінцеві точки | Кінцеві точки, x=0 |
| Критична точка (и) | x=−0.7 Кінцеві точки | x=0, Кінцеві точки |
| Мінімальне значення та місце (и) | (-0.7, -54.45) | (0, 0) |
| Розташування (и) максимального значення | (2, -18) | (-2, 1.59) (2, 1.59) |
Слід зазначити, що зворотне значення теореми екстремальних значень не обов'язково вірно, тобто тільки тому, що f′ (x) =0 в деякому місці x = a, значення функції f (a) не повинно бути локальним мінімумом або максимумом.
Розглянемо\( f(x)=x^3 \nonumber\) і її графік. Ми бачимо, що в той час як f′ (0) =0 при x = 0, x = 0 не є крайньою точкою функції.
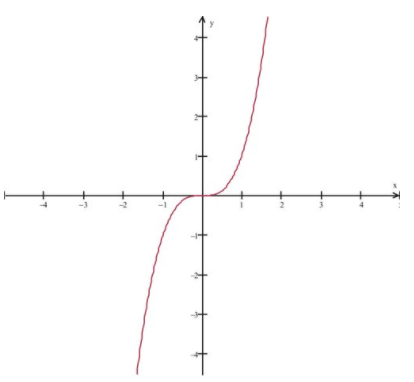
CC ЗА NC-SA
Приклади
Приклад 1
Раніше вас попросили визначити, як пов'язані похідна квадратичної функції\( (y=ax^2+bx+c) \nonumber\) і формула\( x=− \frac{b}{2a} \nonumber\) вершини.
Якщо ви зрозуміли, що вершина квадратичної функції - це також місце, де нахил дотичної лінії, а отже, похідної, дорівнює 0, ви зробили велике спостереження. \( \frac{dy}{dx}=2ax+b=0 \nonumber\)означає, що\( x=− \frac{b}{2a} \nonumber\). Це значення x вершини, і критичне значення або точка функції.
Приклад 2
Функція\( f(x)= \sqrt{25−x^2} \nonumber\) - це верхня частина кола з центром (0, 0) з радіусом 5. Знайдіть критичні точки функції, а також максимуми і мінімуми.
Обчислити похідну:\( f′(x) = \frac{1}{2 \sqrt{25−x^2}}(−2x) = − \frac{x}{ \sqrt{25−x^2}} \nonumber\)
f′ (x) =0 означає, що x = 0 є критичною точкою, а f (0) =5.
Зверніть увагу, що f′ (x) не визначено у двох місцях x = ± 5, що означає, що це критичні точки. Обидва значення пов'язані зі значеннями функції f (±5) =0.
Функція мінімуми знаходяться в (-5, 0) і (5, 0); максимальна функція дорівнює (0, 5).
Рецензія
Для #1 -3 визначити абсолютні і локальні мінімальні і максимальні значення функції (якщо вони існують); знайти крайність. (Одиниці на осях вказують1 одиницю).
- Безперервне ввімк [0, 9]
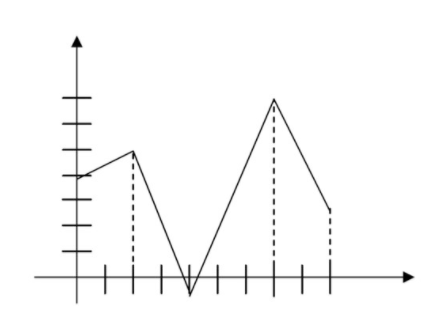
CC ЗА NC-SA
- Безперервне ввімк [0, 9]
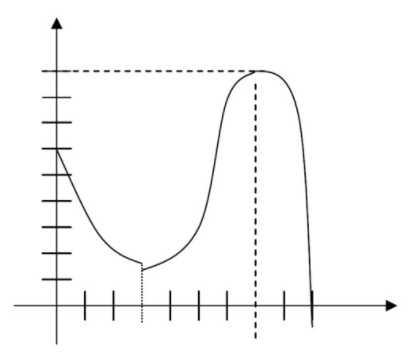
CC ЗА NC-SA
- Безперервний на [0,4] [4,9]
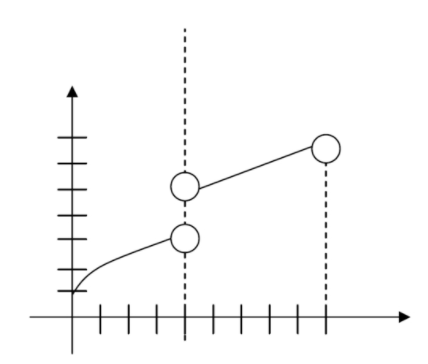
CC ЗА NC-SA
Для #4 —6 знайдіть крайність і намалюйте графік.
- \( f(x)=−x^2−6x+4, [-4, 1] \nonumber\)
- \( f(x)=x^3−x^4, [0, 2] \nonumber\)
- \( f(x)=−x^2+4x^2, [-2, 0] \nonumber\)
- Який абсолютний максимум синусоїдальної функції за інтервал\( [0,π] \nonumber\)?
- Які локальні мінімуми косинусної функції за інтервалом\( [0,2π] \nonumber\)?
- Що таке абсолютний максимум і абсолютний мінімум функції\( x^2 \nonumber\) за інтервал [6, 7]?
- У який момент функція\( f(x)=(x^2−7x−8)^4 \nonumber\) досягає свого абсолютного мінімуму за інтервал [5, 10]?
- Нехай [a, b] буде замкнутим, скінченним інтервалом, а f (x) - прямою лінією. Якщо f (x) досягає свого максимального значення над [a, b] в точках, відмінних від a та b, що повинно бути правдою щодо f (x)?
- Знайти всі критичні числа\( f(x)=3x^4− \frac{8}{3}x^3−6x^2+8x+1 \nonumber\).
- Знайти всі критичні числа\( f(x)=\frac{1}{2x^2−5x−3} \nonumber\).
- Знайти всі критичні числа\( f(x)=ln(x−4) \nonumber\).
- Знайти всі критичні числа\( f(x)=\sqrt{x} ×(1−x) \nonumber\).
- Знайти всі критичні числа\( f(x)= \frac{x^2+x+1}{x−2} \nonumber\).
- Чи досягає многочлен\( f(x)=x^6+x^4+x^2+1 \nonumber\) мінімального значення за інтервал\( [−π,π] \nonumber\)?
- Чи\( f(x)=7^{sin(x)} \nonumber\) досягає функція максимальне значення за інтервал\( (0,π) ] \nonumber\)?
- Чи\( f(x)= \frac{10}{x} \nonumber\) досягає функція максимальне значення за інтервал [-1, 1]?
- Чи\( f(x)=sin( \frac{x}{2}) \nonumber\) досягає функція мінімальне значення за інтервал\( (0,π) \nonumber\)?
- Нехай a і b будуть двома додатними числами, такими, що a<b. Чи функція f (x) = ln (x) досягає максимального значення за інтервал [a, b]?
Огляд (Відповіді)
Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 4.2.
Лексика
| Термін | Визначення |
|---|---|
| критична точка | Критичне значення (або точка) - це значення в замкнутому інтервалі області функції, де або похідна функції в точці дорівнює 0, або похідна не існує. |
| похідний | Похідна функції - нахил прямої дотичної до функції в заданій точці на графіку. Позначення для похідної включають f′ (x),\( \frac{dy}{dx} \nonumber\), y′\( \frac{df}{dx} \nonumber\) та\ frac {df (x)} {dx}. |
| Екстрема | Екстрема - це збірний термін, що охоплює як мінімальне, так і максимальне значення, що відноситься до «екстремальних» значень функції. |
| глобальна крайність | Глобальна крайність функції - це точки зі значеннями y, які є найвищими або найнижчими з усієї функції. |
| Глобальний максимум | Глобальний максимум функції є найбільшим значенням всієї функції. Символічно це найвища точка на всьому графіку. |
| Глобальний мінімум | Глобальний мінімум функції - це найменше значення всієї функції. Символічно це найнижча точка на всьому графіку. |
| локальні екстреми | Локальні екстремуми функції - це точки функції зі значеннями y, які є найвищими або найнижчими з локальної околиці функції. |
| Локальний максимум | Локальний максимум - це найвища точка щодо точок навколо нього. Функція може мати більше одного локального максимуму. |
| Локальний мінімум | Локальний мінімум - найнижча точка щодо точок навколо нього. Функція може мати більше одного локального мінімуму. |
| Максимум | Максимум - це найвища точка графіка. Максимум дасть найбільше значення діапазону. |
| Мінімум | Мінімум - найнижча точка графіка. Мінімум дасть найменшу величину діапазону. |
Додаткові ресурси
PLIX: Грайте, вчіться, взаємодійте, досліджуйте - абсолютна проти локальної екстреми
Відео: L локальний і абсолютний максимум і мінімум
Практика: Абсолютна проти локальної екстреми