2.4: Правила потужності та суми для похідних
- Page ID
- 60365
У наступних кількох розділах ми отримаємо похідні правила, які дозволять нам знайти формули для похідних, коли наша функція приходить до нас як формула. Це дуже алгебраїчний розділ, і ви повинні отримати багато практики. Коли ви говорите комусь, що вивчали обчислення, це той навик, який вони очікуватимуть від вас.
Будівельні блоки
Це найпростіші правила — правила для основних функцій. Ми не будемо доводити ці правила, ми просто скористаємося ними. Але спочатку давайте розглянемо кілька, щоб ми могли бачити, що вони мають сенс.
Знайдіть похідну від\( y=f(x)=mx+b \).
Рішення
Це лінійна функція, тому її графік є власною дотичною лінією! Нахил дотичної лінії, похідної, - це нахил лінії:\[f'(x)=m\nonumber \]
Похідною лінійної функції є її нахил.
Знайдіть похідну від\( f(x)=135 \).
Рішення
Подумайте про це графічно, теж. Графік\(f(x)\) являє собою горизонтальну лінію. Отже, його ухил дорівнює нулю:\[f'(x)=0\nonumber \]
Похідна константи дорівнює нулю.
Знайдіть похідну від\( f(x)=x^2 \).
Рішення
Нагадаємо формальне визначення похідної:\[f'(x)=\lim\limits_{h\to 0} \frac{f(x+h)-f(x)}{h}.\nonumber \]
Використовуючи нашу функцію\( f(x)=x^2 \),\( f(x+h)=(x+h)^2=x^2+2xh+h^2 \).
Тоді\[ \begin{align*} f'(x) & = \lim\limits_{h\to 0} \frac{f(x+h)-f(x)}{h}\\ & = \lim\limits_{h\to 0} \frac{x^2+2xh+h^2-x^2}{h}\\ & = \lim\limits_{h\to 0} \frac{2xh+h^2}{h}\\ & = \lim\limits_{h\to 0} \frac{h(2x+h)}{h}\\ & = \lim\limits_{h\to 0} (2x+h)\\ & = 2x \end{align*} \nonumber \]
З усього цього ми знаходимо це\( f'(x)=2x \).
На щастя, є зручне правило, яке ми використовуємо, щоб пропустити використання ліміту:
Похідна від\( f(x)=x^n \) is \[f'(x)=nx^{n-1}.\nonumber \]
Знайдіть похідну від\( g(x)=4x^3 \).
Рішення
Використовуючи правило харчування, ми знаємо, що якщо\( f(x)=x^3 \), то\( f'(x)=3x^2 \). Зверніть увагу,\(g\) що в 4 рази більше функції\(f\). Подумайте про те, що ця зміна означає для графіка\(g\) - тепер вона в 4 рази вище, ніж графік\(f\). Якщо ми знайдемо нахил січної лінії, це буде\( \frac{\Delta g}{\Delta x}= \frac{4\Delta f}{\Delta x} =4\frac{\Delta f}{\Delta x} \); кожен нахил буде в 4 рази більше нахилу січної лінії на\(f\) графіку. Ця властивість буде триматися і для нахилів дотичних ліній, теж:\[\frac{d}{dx}\left(4x^3\right)=4\frac{d}{dx}\left(x^3\right)=4\cdot 3x^2=12x^2.\nonumber \]
Константи приходять для їзди, т. Е.\( \frac{d}{dx}\left( kf\right)=kf'.\)
Ось всі основні правила в одному місці.
У чому випливає,\(f\) і\(g\) диференційовані функції\(x\).
Постійне множинне правило
\[ \frac{d}{dx}\left( kf\right)=kf'\nonumber \]
Правило суми та різниці
\[\frac{d}{dx}\left(f\pm g\right)=f' \pm g'\nonumber \]
Правило влади
\[\frac{d}{dx}\left(x^n\right)=nx^{n-1}\nonumber \]
Особливі випадки:\[\frac{d}{dx}\left(k\right)=0 \quad \text{(Because \( k=kx^0 \).)}\nonumber \]\[\frac{d}{dx}\left(x\right)=1 \quad \text{(Because \( x=x^1 \).)}\nonumber \]
Експоненціальні функції
\[\frac{d}{dx}\left(e^x\right)=e^x\nonumber \]\[\frac{d}{dx}\left(a^x\right)=\ln(a)\,a^x\nonumber \]
Натуральний логарифм
\[\frac{d}{dx}\left(\ln(x)\right)=\frac{1}{x}\nonumber \]
Сума, різниця та постійне кратне правило в поєднанні з правилом влади дозволяють легко знайти похідну будь-якого многочлена.
Знайдіть похідну від\( p(x)=17x^{10}+13x^8-1.8x+1003 \).
Рішення
\[ \begin{align*} \frac{d}{dx}\left( 17x^{10}+13x^8-1.8x+1003 \right) & = \frac{d}{dx}\left( 17x^{10} \right)+\frac{d}{dx}\left( 13x^8 \right)-\frac{d}{dx}\left( 1.8x \right)+\frac{d}{dx}\left( 1003 \right)\\ & = 17\frac{d}{dx}\left( x^{10} \right)+13\frac{d}{dx}\left( x^8 \right)-1.8\frac{d}{dx}\left( x \right)+\frac{d}{dx}\left( 1003 \right)\\ & = 17\left(10x^9\right)+13\left(8x^7\right)-1.8\left(1\right)+0\\ & = 170x^9+104x^7-1.8 \end{align*} \nonumber \]
Вам не потрібно показувати кожен крок. Будьте обережні, коли ви вперше працюєте з правилами, але досить скоро ви зможете просто записати похідну безпосередньо:
Знайти\(\frac{d}{dx}\left( 17x^2-33x+12 \right)\).
Рішення
Виписуючи правила, ми б написали\[\frac{d}{dx}\left( 17x^2-33x+12 \right)=17(2x)-33(1)+0=34x-33.\nonumber \]
Після того, як ви ознайомилися з правилами, ви можете, в голові, помножити 2 рази 17 і 33 на 1, і просто написати\[\frac{d}{dx}\left( 17x^2-33x+12 \right)=34x-33.\nonumber \]
Правило харчування працює навіть в тому випадку, якщо потужність негативна або дріб. Для того щоб його застосувати, спочатку перекладіть всі коріння і основні раціональні вирази в показники:
Знайдіть похідну від\( y=3\sqrt{t}-\frac{4}{t^4}+5e^t \).
Рішення
Першим кроком є переклад в експоненти:\[y=3\sqrt{t}-\frac{4}{t^4}+5e^t=3t^{1/2}-4t^{-4}+5e^t\nonumber \]
Тепер можна взяти похідну:\[ \begin{align*} \frac{d}{dt}\left( 3t^{1/2}-4t^{-4}+5e^t \right) & = 3\left(\frac{1}{2}t^{-1/2}\right)-4\left(-4t^{-5}\right)+5\left(e^t\right) \\ & = \frac{3}{2}t^{-1/2}+16t^{-5}+5e^t \end{align*} \nonumber \]
Якщо є причина, можна переписати відповідь з радикалами і позитивними показниками:\[y'= \frac{3}{2}t^{-1/2}+16t^{-5}+5e^t= \frac{3}{2\sqrt{t}}+\frac{16}{t^5}+5e^t\nonumber \]
Будьте обережні при знаходженні похідних з негативними показниками.
Ми можемо відразу застосувати ці правила для вирішення проблеми, з якої ми почали главу - знаходження дотичної лінії.
Знайти рівняння прямої дотичної до\( g(t)=10-t^2 \) коли\(t = 2\).
Рішення
Нахил дотичної лінії - це величина похідної. Ми можемо обчислити\( g'(t)=-2t \). Щоб знайти нахил дотичної лінії при\(t = 2\), оцініть похідну в цій точці. Ухил дотичної лінії дорівнює -4.
Щоб знайти рівняння дотичної прямої, нам також знадобиться точка на дотичній лінії. Оскільки дотична лінія стосується вихідної функції at\(t = 2\), ми можемо знайти точку, оцінивши вихідну функцію:\( g(2)=10-2^2=6 \). Дотична лінія повинна проходити через точку (2, 6).
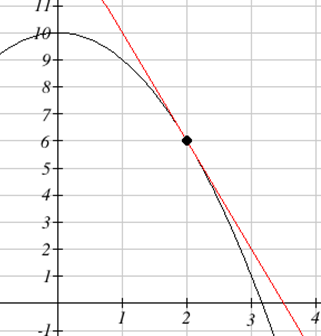
Використовуючи рівняння точки-нахилу прямої, дотична лінія матиме рівняння\( y-6=-4(t-2) \). Спрощуючи форму ухил-перехоплення, рівняння є\( y=-4t+14 \).
Графікуючи, ми можемо переконатися, що ця лінія дійсно дотична до кривої:
Ми також можемо використовувати ці правила, щоб допомогти нам знайти похідні, які нам потрібні для інтерпретації поведінки функції.
В експерименті з пам'яттю дослідник просить суб'єкта запам'ятати якомога більше слів зі списку за 10 секунд. Відкликання тестується, потім випробуваному дається ще 10 секунд на вивчення і так далі. Припустимо, кількість слів, що запам'ятовуються після\(t\) секунд вивчення, може бути змодельована\( W(t)=4t^{2/5} \). Знайти і інтерпретувати\( W'(20) \).
Рішення
\( W'(t)=4\cdot \frac{2}{5}t^{-3/5}=\frac{8}{5}t^{-3/5} \), Отже\( W'(20)=\frac{8}{5}(20)^{-3/5}\approx 0.2652 \).
Так як\(W\) вимірюється в словах, і\(t\) знаходиться в секундах,\(W'\) має одиниці слів в секунду. \( W'(20)\approx 0.2652 \)означає, що після 20 секунд навчання суб'єкт вивчає приблизно 0,27 більше слів за кожну додаткову секунду навчання.
Умови бізнесу та економіки
Далі ми більш глибоко заглибимося в деякі бізнес-додатки. Для цього нам спочатку потрібно переглянути деяку термінологію.
Припустимо, ви виробляєте і продаєте якийсь товар. Прибуток, який ви робите, це сума грошей, яку ви берете в мінус те, що ви повинні заплатити, щоб виробляти предмети. Обидві ці кількості залежать від того, скільки ви робите і продаєте. (Таким чином, у нас є функції тут.) Ось список визначень для деяких термінологій, разом з їх значенням в алгебраїчних термінологіях і в графічному плані.
Ваша вартість - це гроші, які ви повинні витратити, щоб виробляти ваші предмети.
Фіксована вартість (FC) - це сума грошей, яку ви повинні витратити незалежно від того, скільки предметів ви виробляєте. FC може включати такі речі, як оренда, витрати на придбання техніки та зарплати для офісного персоналу. Ви повинні платити постійні витрати, навіть якщо ви нічого не виробляєте.
Загальна змінна вартість (TVC) для\(q\) items is the amount of money you spend to actually produce them. TVC includes things like the materials you use, the electricity to run the machinery, gasoline for your delivery vans, maybe the wages of your production workers. These costs will vary according to how many items you produce.
Загальна вартість (TC, або іноді просто C) для\(q\) позицій - це загальна вартість їх виробництва. Це сума фіксованої вартості та загальної змінної вартості для виробництва\(q\) виробів.
Середня вартість (AC) для\(q\) позицій - це загальна вартість, поділена на\(q\), або
\[AC(q) = \frac{TC}{q}\nonumber \]
Також можна говорити про середню фіксовану вартість\(\frac{FC}{q}\), або середню змінну вартість,\(\frac{TVC}{q}\).
Маржинальна вартість (MC) на\(q\) позиціях - це вартість виробництва наступної позиції. Дійсно, це\[MC(q) = TC(q + 1) - TC(q).\nonumber \] У багатьох випадках, однак, простіше наблизити цю різницю за допомогою обчислення (див. Приклад 1 нижче). І деякі джерела визначають граничну вартість безпосередньо як похідну,\[MC(q) = TC'(q).\nonumber \] У цьому курсі ми будемо використовувати обидва ці визначення так, ніби вони були взаємозамінними.
Одиниці по граничній вартості - це вартість за одиницю товару.
Для цілей цього курсу, якщо питання запитує граничні витрати, дохід, прибуток тощо, обчислити його, якщо це можливо, використовуючи похідну, якщо це можливо, якщо спеціально не сказано інше.
Чому це нормально, що існує два визначення граничних витрат (і граничного доходу та маржинального прибутку)?
Ми використовували нахили січних ліній протягом крихітних інтервалів для наближення похідних. У цьому прикладі ми повернемо це навколо - ми будемо використовувати похідну для наближення нахилу січної лінії.
Зверніть увагу, що визначення «вартість наступного пункту» насправді є нахилом січної лінії, через інтервал 1 одиниці:\[MC(q) = C(q + 1) - 1 = \frac{C(q+1)-1}{1}.\nonumber \]
Отже, це приблизно те ж саме, що похідна від функції витрат на q:\[MC(q) = C'(q).\nonumber \]
На практиці ці два числа настільки близькі, що немає практичних підстав розрізняти. Для наших цілей гранична вартість є похідною - це вартість наступного пункту.
У таблиці вказана загальна вартість (ТК) вироблених\(q\) виробів.
| Предмети,\( q \) | ТК |
| 0 | $20,000 |
| 100 | $35,000 |
| 200 | 45 000 доларів |
| 300 | $53 000 |
- Що таке фіксована вартість?
- Коли виготовляється 200 найменувань, яка загальна змінна вартість? Середня змінна вартість?
- Коли виготовлено 200 найменувань, оцініть граничну вартість.
Рішення
- Фіксована вартість становить 20 000 доларів, вартість навіть тоді, коли елементи не зроблені.
- Коли виготовлено 200 предметів, загальна вартість становить 45 000 доларів. Віднімаючи фіксовану вартість, загальна змінна вартість становить $45 000 - $20 000 = $25 000.
Середня змінна вартість - це загальна змінна вартість, поділена на кількість елементів, тому ми розділимо загальну змінну вартість 25 000 доларів на 200 зроблених елементів. 25 000/200 = 125 доларів. В середньому кожен товар мав змінну вартість 125 доларів.
- Нам потрібно оцінити величину похідної, або нахил дотичної прямої в\(q = 200\). Знаходження січної лінії від\(q=100\) до\(q=200\) дає нахил\[ \frac{45,000-35,000}{200-100}=100.\nonumber \]
Знаходження січної лінії від\(q=200\) до\(q=300\) дає нахил\[\frac{53,000-45,000}{300-200}=80.\nonumber \]
Ми могли б оцінити дотичний нахил, усереднивши ці січні схили, даючи нам оцінку $90/елемент.
Це говорить нам про те, що після того, як буде виготовлено 200 предметів, це буде коштувати близько 90 доларів, щоб зробити ще один предмет.
Вартість виготовлення\(x\) виробів становить\(C(x) = \sqrt{x}\) сто доларів.
- Яка вартість виготовлення 100 найменувань? 101 пунктів? Яка вартість 101-го товару?
- Розрахувати\(C '(x)\) і оцінити\(C '\) на\(x = 100\). Як\(C '(100)\) порівнюється з останньою відповіддю в частині а?
Рішення
- \(C(100) =\)10 сотень доларів = 1000 доларів і\(C(101) =\) 10,0499 сотень доларів = $1004,99, тому це коштує $4.99 для цього 101-го елемента. Використовуючи це визначення, гранична вартість становить $4.99.
- \( C'(x)=\frac{1}{2}x^{-1/2} = \frac{1}{2\sqrt{x}}\), Таким чином,\( C'(100)=\frac{1}{2\sqrt{100}}=\frac{1}{20} \) сто доларів = $5.00.
Зверніть увагу, наскільки близькі ці відповіді! Це показує (знову), чому це нормально, що ми використовуємо обидва визначення граничної вартості.
Попит - це функціональна залежність між ціною\(p\) та кількістю\(q\), яку можна продати (тобто вимагати). Залежно від вашої ситуації, ви можете думати про\(q\) функцію або\(q\) як функцію\(p\)\(p\)
Ваш дохід - це сума грошей, яку ви фактично берете від продажу вашої продукції.
Загальний дохід (TR, або просто R) для\(q\) предметів - це загальна сума грошей, яку ви берете на продаж\(q\) товарів. Загальний дохід - це ціна, помножена на кількість,\[TR = p \cdot q.\nonumber \]
Середній дохід (AR) для\(q\) позицій - це загальний дохід, поділений на\(q\), або\[\frac{TR}{q}.\nonumber \]
Маржинальний дохід (MR) на\(q\) позиціях - це дохід від виробництва наступного товару,\[MR(q) = TR(q + 1) - TR(q).\nonumber \]
Так само, як і при граничній вартості, ми будемо використовувати як це визначення, так і похідне визначення:\[MR(q) = TR'(q).\nonumber \]
Ваш прибуток - це те, що залишилося від загального доходу після віднімання витрат.
Прибуток (P) для\(q\) статей - це різниця\[TR(q) - TC(q),\nonumber \] між загальною виручкою та загальними витратами.
Середній прибуток за\(q\) статтями становить\[\frac{P}{q}.\nonumber \]
Маржинальний прибуток за\(q\) статтями становить\[P(q + 1) – P(q),\nonumber \] або\[P'(q)\nonumber \]
Графічні інтерпретації основних термінів бізнес-математики
Ілюстрація
Ось графіки ТР і ТК для виробництва і продажу певного товару. Горизонтальна вісь - це кількість предметів, в тисячах. Вертикальна вісь - це кількість доларів, також у тисячах.
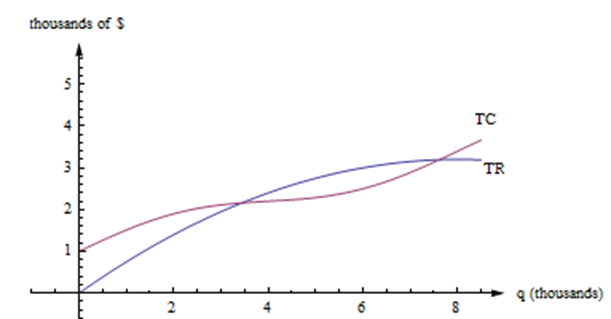
По-перше, зверніть увагу, як знайти фіксовану вартість і змінну вартість з графіка тут. ФК -\(y\) перехоплення графа ТК. (\(FC = TC(0)\).) Графік ТВК мав би таку ж форму, як і графік ТК, зміщений вниз. (\(TVC = TC - FC\).)
\(MC(q) = TC(q + 1) - TC(q)\), але це неможливо прочитати на цьому графіку. Як можна було відрізнити ТК (4022) і ТК (4023)? На цьому графіку цей інтервал занадто малий, щоб побачити, і наша найкраща здогадка на січній лінії насправді дотична лінія до кривої TC в цій точці. (Це причина, по якій ми хочемо мати похідне визначення під рукою.)
\(MC(q)\)- нахил дотичної лінії до кривої ТК в\( (q, TC(q))\).
\(MR(q)\)- нахил дотичної лінії до кривої ТР в\((q, TR(q))\).
Прибуток - це відстань між кривою ТР і ТС. Якщо ви поекспериментуєте з чіткою лінійкою, ви побачите, що найбільший прибуток відбувається саме тоді, коли дотичні лінії до кривих TR і TC паралельні. Це правило, прибуток максимізується\( MR = MC\), коли
ми розглянемо пізніше в розділі.
Попит\(D\), на товар за ціною\(p\) доларів, дається\( D(p)=200-0.2p^2 \). Знайдіть граничний дохід, коли ціна становить 10 доларів.
Рішення
Для початку нам потрібно сформувати рівняння доходу. Оскільки дохід = Ціна\( \times \) Кількість, а рівняння попиту показує кількість товару, який можна продати, ми маємо\[R(p)=D(p)\cdot p=\left(200-0.2p^2\right)p=200p-0.2p^3.\nonumber \]
Тепер ми можемо знайти граничний дохід, знайшовши похідну:\[R'(p)=200(1)-0.2(3p^2)=200-0.6p^2\nonumber \]
За ціною $10,\( R'(10)=200-0.6(10)^2=140 \).
Зверніть увагу на одиниці для\(R'\) є\(\frac{\text{dollars of Revenue}}{\text{dollar of price}}\), так це\( R'(10)=140 \) означає, що коли ціна становить $10, дохід буде збільшуватися на $140 за кожен долар, що ціна була збільшена.
