2.2: Межі та безперервність
- Page ID
- 60374
Обмеження
В останньому розділі ми побачили, що в міру того, як інтервал, за який ми розрахували, став менше, січні укоси наближалися до дотичному схилу. Межа дає нам кращу мову, з якою можна обговорювати ідею «підходів».
Межа функції описує поведінку функції, коли змінна знаходиться поруч, але не дорівнює вказаному числу (див. Малюнок нижче).
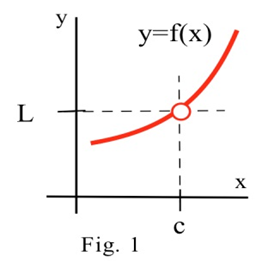
Якщо значення наближаються і\(f(x)\) ближче, як ми хочемо, до одного числа,\(L\) як ми приймаємо значення\(x\) дуже близьких до (але не рівних) числа\(c\), то ми говоримо "межа\(f(x)\) як\(x\) підходів\(c\) є\(L\)" і пишемо \[\lim\limits_{x\to c} f(x)=\mathbf{L}.\nonumber \]Символ "\( \to \)" означає «наближається» або, менш формально, «наближається до».
(Це визначення межі не викладено так формально, як могло б бути, але цього достатньо для наших цілей у цьому курсі.)
Примітка:
- \(\bf f(c)\)є єдиним числом, яке описує поведінку (значення)\(f(x)\) AT точки\(x = c\).
- \(\lim\limits_{x\to c} f(x)\)це єдине число, яке описує поведінку\(f(x)\) NEAR, АЛЕ НЕ AT, точка\(x = c\).
Якщо у нас є графік функції поруч\(x = c\), то його зазвичай легко визначити\( \lim\limits_{x\to c} f(x) \).
(Ось посилання на зображення, використані в наступному відео, а також в інших місцях цього розділу: Графіки для обмежень і Приклади безперервності.)
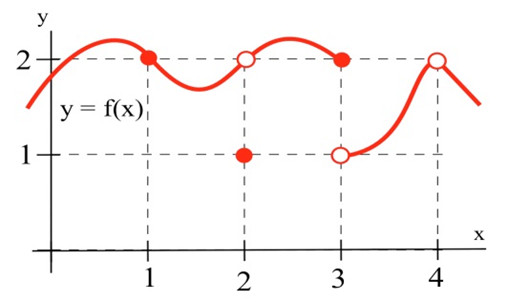
Використовуйте графік на\(y = f(x)\) малюнку нижче, щоб визначити наступні межі:
- \(\lim\limits_{x\to 1} f(x)\)
- \(\lim\limits_{x\to 2} f(x)\)
- \(\lim\limits_{x\to 3} f(x)\)
- \(\lim\limits_{x\to 4} f(x)\)
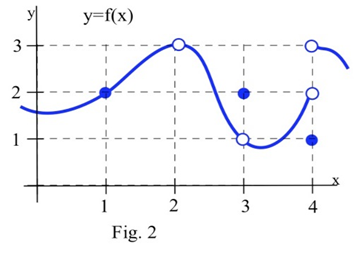
Рішення
- \[\lim_{x \to 1} f(x) = 2\nonumber\]Коли\(x\) дуже близький до 1, значення\(f(x)\) дуже близькі до\(y = 2\). У цьому прикладі трапляється так\(f(1) = 2\), але це не має значення для ліміту. Єдине, що важливо, це те, що відбувається для\(x\) близьких до 1 але\(x \neq 1\).
- \(f(2)\)не визначено, але ми дбаємо лише про поведінку\(f(x)\) для\(x\) близьких до 2, але не дорівнює 2. Коли\(x\) близький до 2, значення\(f(x)\) близькі до 3. Якщо ми\(x\) обмежимося досить близько до 2, значення\(y\) буде так близько до 3, як ми хочемо, так\( \lim\limits_{x\to 2} f(x) = 3 \).
- Коли\(x\) наближається до 3 (або «як\(x\) наближається до значення 3"), значення\(f(x)\) близькі до 1 (або «наближаються до значення 1»), так\( \lim\limits_{x\to 3} f(x) = 1 \). Для цієї межі абсолютно не має значення\(f(3) = 2\), що, Ми дбаємо лише про те, що відбувається\(f(x)\) для\(x\) близьких і не дорівнює 3.
- Це важче, і ми повинні бути обережними. Коли\(x\) близький до 4 і трохи менше 4 (\(x\)знаходиться зліва від 4 на\(x\) -осі), то значення\(f(x)\) близькі до 2. Але якщо\(x\) близький до 4 і трохи більше 4, то значення\(f(x)\) близькі до 3. Якщо ми знаємо лише, що\(x\) дуже близько до 4, то ми не можемо сказати, чи\(y = f(x)\) буде близько 2 або близько до 3 - це залежить від того, чи\(x\) знаходиться справа чи ліва сторона 4. У цій ситуації\(f(x)\) значення не близькі до одного числа, тому ми говоримо, що\(\lim\limits_{x\to 4} f(x)\) не існує. Це не має значення\(f(4) = 1\). Межа, як\(x\) наближається до 4, все одно буде невизначеною, якщо б\(f(4)\) було 3 або 2 або що-небудь ще.
Ми також можемо досліджувати обмеження за допомогою таблиць та алгебри.
Знайти\( \lim\limits_{x\to 1} \dfrac{2x^2-x-1}{x-1} \).
Рішення
Ви можете спробувати оцінити\(f(x) = \frac{2x^2-x-1}{x-1}\) на\(x = 1\), але\(f(x)\) не визначено в\(x = 1\). Спокусливо, але неправильно зробити висновок, що ця функція не має межі, як\(x\) наближається 1.
Використання таблиць: Спробувавши деякі «тестові» значення, для\(x\) яких наближаємося до 1 як зліва, так і справа, отримуємо
| \( x \) | \( f(x) \) |
|---|---|
| \ (x\) ">0.9 | \ (f (x)\) ">2.82 |
| \ (x\) ">0,9998 | \ (f (x)\) ">2,9996 |
| \ (х\) ">0,999994 | \ (ф (х)\) ">2,999988 |
| \ (х\) ">0,9999999 | \ (ф (х)\) ">2,9999998 |
| \ (x\) ">\( \to 1 \) | \ (f (x)\) ">\( \to 3 \) |
| \( x \) | \( f(x) \) |
|---|---|
| \ (x\) ">1.1 | \ (f (x)\) ">3.2 |
| \ (х\) ">1,003 | \ (ф (х)\) ">3,006 |
| \ (х\) ">1.0001 | \ (f (x)\) ">3.0002 |
| \ (х\) ">1.000007 | \ (ф (х)\) ">3.000014 |
| \ (x\) ">\( \to 1 \) | \ (f (x)\) ">\( \to 3 \) |
\(f\)Функція не визначена в\(x = 1\), але коли\(x\) близька до 1, значення\(f(x)\) наближаються до 3. Ми можемо\(f(x)\) наблизитися до 3, як ми хочемо, взявши\(x\) дуже близько до 1 так\[\lim\limits_{x\to 1} \dfrac{2x^2-x-1}{x-1}=3.\nonumber \]
Використання алгебри: Ми могли б знайти той самий результат, зазначивши, що до тих\[ f(x)= \dfrac{2x^2-x-1}{x-1} = \dfrac{(2x+1)(x-1)}{(x-1)} = 2x+1\nonumber \] пір, поки\(x \neq 1\). (Якщо\(x\neq 1\), то\(x–1 \neq 0\) так справедливо розділити чисельник і знаменник на множник\(x–1\).) "\(x\to 1\)" частина межі означає, що\(x\) близька до 1, але не дорівнює 1, тому наш крок поділу є дійсним\[ \lim\limits_{x\to 1}\dfrac{2x^2-x-1}{x-1} = \lim\limits_{x\to 1} 2x+1 = 3,\nonumber \], і це наша відповідь.
Використання графіка: Ми можемо графік\( y=f(x)= \dfrac{2x^2-x-1}{x-1} \) для\(x\) близьких до 1:
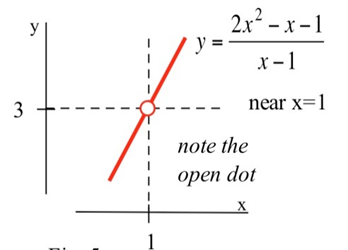
Зверніть увагу,\(x\) що кожного разу, коли близький до 1, значення\(y = f(x)\) близькі до 3. Оскільки\(f\) не визначено в\(x = 1\), графік має отвір вище\(x = 1\), але ми дбаємо лише про те, що\(f(x)\) робиться для\(x\) близького, але не дорівнює 1.
Знайти\(\lim \limits_{x\to 3} \dfrac{\frac{1}{x} -\frac{1}{3} }{x-3}\).
Рішення
Зверніть увагу, що ця функція не визначена на\(x = 3\). Ми можемо знайти межу за допомогою алгебри. Надавши два члени в чисельнику спільний знаменник, можна спростити:
\[ \frac{\frac{1}{x} -\frac{1}{3} }{x-3} = \frac{\frac{1}{x} \cdot \frac{3}{3} -\frac{1}{3} \cdot \frac{x}{x} }{x-3} = \frac{\frac{3}{3x} -\frac{x}{3x} }{x-3} =\frac{\frac{3-x}{3x} }{x-3} \nonumber \]
Пам'ятайте, що ділення дробу - це те саме, що множення на зворотну,
\[\frac{\frac{3-x}{3x} }{x-3} =\frac{\frac{3-x}{3x} }{\frac{x-3}{1} }\nonumber \] тому еквівалентно\[\frac{3-x}{3x} \cdot \frac{1}{x-3}\nonumber \]
Щоб спростити далі, нам потрібно перерахувати негативний 1 з чисельника. Тоді ми можемо скасувати термін до тих\(\left(x-3\right)\)
\(\dfrac{-1(x-3)}{3x} \cdot \dfrac{1}{x-3} =\dfrac{-1}{3x}\) пір, поки\(x \neq 3\)
Тепер ми можемо оцінити ліміт, використовуючи цю спрощену форму.
\[\lim\limits_{x\to 3} \frac{\frac{1}{x} -\frac{1}{3} }{x-3} = \lim\limits_{x\to 3} \frac{-1}{3x} = -\frac{1}{9} \nonumber \]
Односторонні межі
Іноді те, що відбувається з нами на місці, залежить від напрямку, який ми використовуємо для наближення до цього місця. Якщо ми наблизимось до Ніагарського водоспаду з боку вище за течією, то ми будемо на 182 фути вище і матимемо різні турботи, ніж якщо ми підходимо з нижньої сторони. Аналогічно, значення функції поблизу точки можуть залежати від напрямку, який ми використовуємо для наближення до цієї точки.
Ліва\(f(x)\) межа як\(x\)\(c\) підходи,\(L\) якщо значення\(f(x)\) отримати якомога ближче до того,\(L\) як ми хочемо, коли\(x\) дуже близько і зліва від\(c\) (тобто,\(x \lt \mathbf{c}\)). пишемо\[\lim\limits_{x\to c^-} f(x)=L.\nonumber \]
Права\(f(x)\) межа як\(x\) підходи\(c\), написані з\(\bf x \to c^+\), є\(L\) якщо значення\(f(x)\) отримати так близько до,\(L\) як ми хочемо, коли\(x\) дуже близько і праворуч від\(c\) (тобто,\(x \gt \mathbf{c}\)). пишемо\[\lim\limits_{x\to c^+} f(x)=L.\nonumber \]
Оцініть односторонні межі функції,\(f(x)\) наведеної нижче в\(x = 0\) і\(x = 1\).
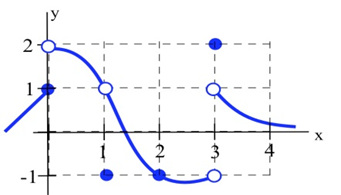
Рішення
У міру\(x\) наближення 0 зліва значення функції наближається до 1, тому\( \lim\limits_{x\to 0^-} f(x) = 1. \)
Коли справа\(x\) наближається до 0, значення функції наближається до 2, тому\( \lim\limits_{x\to 0^+} f(x) = 2. \)
Зверніть увагу, що так як ліміт зліва і ліміт справа різні, то загальний ліміт\( \lim\limits_{x\to 0} f(x) \), не виходить.
При\(x\) підходах 1 з будь-якого напрямку значення функції наближається до 1, тому\[\lim\limits_{x\to 1^-} f(x) = \lim\limits_{x\to 1^+} f(x) = \lim\limits_{x\to 1} f(x) = 1. \nonumber \]
Безперервність
Функція, яка є «дружньою» і не має ніяких перерв або стрибків, називається безперервною. Більш формально,
Функція\(\bf f\) є безперервною,\(\bf x = a \) якщо і тільки якщо\( \lim\limits_{x\to a} \mathbf{f(x)} = \mathbf{f(a)}\).
Графік нижче ілюструє деякі різні способи, якими функція може вести себе в точці та поблизу неї, а таблиця містить деяку числову інформацію про функцію та її поведінку.
| \( a \) | \( f(a) \) | \( \lim\limits_{x\to a} f(x) \) |
| 1 | 2 | 2 |
| 2 | 1 | 2 |
| 3 | 2 | Не існує (DNE) |
| 4 | Невизначений | 2 |
Виходячи з інформації в таблиці, можна зробити висновок, що\(f\) є безперервним при 1 з\( \lim\limits_{x\to 1} f(x) = 2 = f(1)\).
Ми також можемо зробити висновок з інформації в таблиці, яка не\(f\) є безперервною на 2 або 3 або 4, тому що\( \lim\limits_{x\to 2} f(x) \neq f(2) \),\( \lim\limits_{x\to 3} f(x) \neq f(3) \), і\( \lim\limits_{x\to 4} f(x) \neq f(4) \).
Поведінка на\(x = 2\) і\(x = 4\) демонструє дірку в графіку, іноді її називають знімним розривом, оскільки графік можна зробити безперервним, змінюючи значення однієї точки. Поведінка при\( x = 3 \) називається розривом стрибка, так як графік перескакує між двома значеннями.
Отже, які функції є безперервними? Виявляється, майже кожна функція, яку ви вивчали, є безперервною, де вона визначена: поліноміальні, радикальні, раціональні, експоненціальні та логарифмічні функції є безперервними, де вони визначені. Більш того, будь-яка комбінація безперервних функцій також є безперервною.
Це корисно, тому що визначення безперервності говорить про те, що для безперервної функції,\( \lim\limits_{x\to a} f(x) = f(a) \). Це означає, що для безперервної функції ми можемо знайти межу шляхом прямої підстановки (оцінки функції), якщо функція є безперервною в\(a\).
Оцініть, використовуючи безперервність, якщо це можливо:
- \( \lim\limits_{x\to 2} x^3-4x \)
- \( \lim\limits_{x\to 2} \dfrac{x-4}{x+3} \)
- \( \lim\limits_{x\to 2} \dfrac{x-4}{x-2} \)
Рішення
- Дана функція є поліноміальною і визначається для всіх значень\(x\), тому ми можемо знайти межу шляхом прямої підстановки:\[ \lim\limits_{x\to 2} x^3-4x = 2^3-4(2) = 0. \nonumber \]
- Дана функція є раціональною. Вона не визначена в\(x = -3\), але ми приймаємо межу як\(x\) наближається 2, і функція визначається в цьому місці, тому ми можемо використовувати пряму підстановку:\[ \lim\limits_{x\to 2} \dfrac{x-4}{x+3} = \dfrac{2-4}{2+3}= -\dfrac{2}{5}. \nonumber \]
- Ця функція не визначена в\(x = 2\), і тому не є безперервною при\(x = 2\). Ми не можемо використовувати пряму заміну.
