1.17: Кути

Вам знадобиться калькулятор в кінці цього модуля.

кутова шліфувальна машина

Вимірювання кута має важливе значення в будівництві, геодезії, фізичній терапії та багатьох інших сферах. Ми можемо візуалізувати кут як фігуру, утворену, коли два відрізки лінії мають спільну кінцеву точку. Ми також можемо думати про кут як міру обертання. Повне обертання або повне коло є$360^\circ$, тому половина обертання або розворот є$180^\circ$, а чверть обороту - це$90^\circ$.

Ми часто класифікуємо кути за їх розмірами.

• Гострий кут: між$0^\circ$ і$90^\circ$
• Прямий кут: точно$90^\circ$
• Тупий кут: між$90^\circ$ і$180^\circ$
• Прямий кут: точно$180^\circ$
• Рефлексивний кут: між$180^\circ$ і$360^\circ$

Лінії, що утворюють$90^\circ$ кут, називаються перпендикулярними. Як показано нижче, голка повинна бути перпендикулярна поверхні тіла для внутрішньом'язової ін'єкції.

Вправи$\PageIndex{1}$

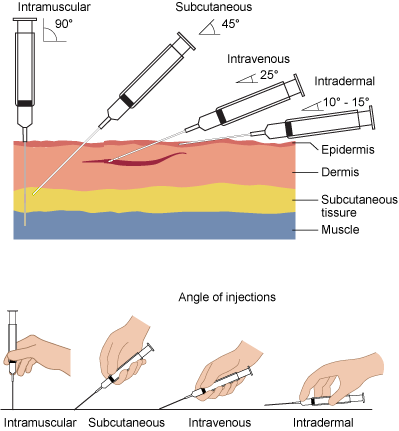
Визначте кожен кут, показаний нижче, як гострий, правий, тупий, прямий або рефлексивний.

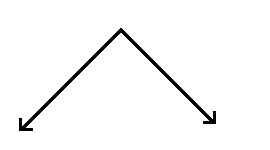
1.

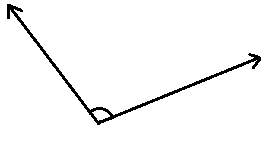
2.

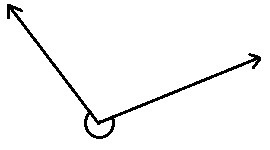
3.

4.

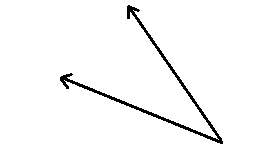
5.

Знайдіть міру кожного невідомого кута.

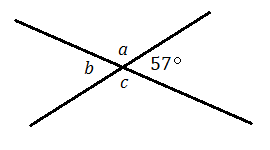
6.

Відповідь

1. прямий кут

2. тупий кут

3. рефлексивний кут

4. прямий кут

5. гострий кут

6. $a=123^\circ$$b=57^\circ$;$c=123^\circ$

Кути в трикутниках

Якщо потрібно знайти мірки кутів в трикутнику, є кілька правил, які можуть допомогти.

Сума кутів кожного трикутника дорівнює$180^\circ$.

Якщо будь-які сторони трикутника мають рівні довжини, то кути, протилежні цим сторонам, матимуть рівні міри.

Вправи$\PageIndex{1}$

Знайдіть міри невідомих кутів у кожному трикутнику.

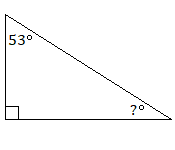
7.

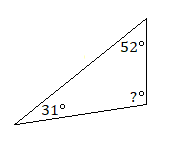
8.

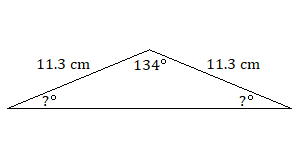
9.

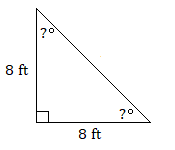
10.

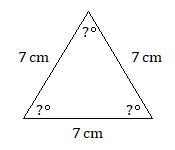
11.

Відповідь

7. $37^\circ$

8. $97^\circ$

9. $23^\circ$кожен

10. $45^\circ$кожен

11. $60^\circ$кожен

Кути і паралельні лінії

Дві лінії, які вказують в одному напрямку і ніколи не перетинаються, називаються паралельними лініями. Якщо дві паралельні лінії перетинаються третьою лінією, утворюються набори однакових за розміром кутів, як показано на наступній схемі. Всі чотири гострі кути будуть рівні за мірою, всі чотири тупих кута будуть рівні за мірою, а будь-який гострий кут і тупий кут матимуть комбіновану міру$180^\circ$.

Приклад$\PageIndex{1}$

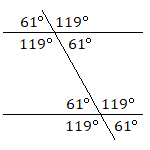
Знайдіть міри кутів$A$$B$, і$C$.

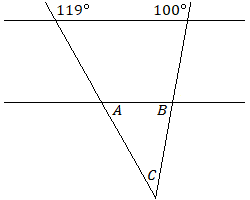
Рішення

А. 61°

Б. 80°

C. 39°

Градуси, Хвилини, Секунди

Можна мати кутові заходи, які не є цілим числом градусів. У цих ситуаціях прийнято використовувати десяткові знаки, але старий метод, який називається градуси-хвилини-секунди або системою DMS - ділить ступінь, використовуючи дроби з$60$: хвилина -$\dfrac{1}{60}$ градус, а секунда -$\dfrac{1}{60}$ хвилини, що означає, що секунда є$\dfrac{1}{3,600}$ ступеня. (На щастя, ці перетворення працюють точно так само, як час; думайте про$1$ ступінь як$1$ годину.) Наприклад,$2.5^\circ=2^\circ30'$.

Ми розглянемо процедуру перетворення між системами, але є онлайн-калькулятори, такі як той, який за адресою https://www.fcc.gov/media/radio/dms-decimal, який зробить перетворення за вас.

Якщо у вас є широта і довгота в DMS, як N$18^\circ54'40''$ W$155^\circ40'51''$, і вам потрібно перетворити його в десяткові градуси, процес досить простий за допомогою калькулятора.

Перетворення з DMS в десяткові градуси

Введіть$\text{degrees}+\text{minutes}\div60+\text{seconds} \div 3600$ у свій калькулятор. Округляйте результат до четвертого знака після коми, якщо це необхідно. ^[1]

Вправи$\PageIndex{1}$

Перетворіть кожне вимірювання кута з градусів-хвилин-секунд у десяткову форму. Округлити до найближчих десятитисячних, якщо це необхідно.

13. $67^\circ48'54''$

14. $19^\circ37'25''$

15. $34^\circ14'12''$

Відповідь

13. $67.815^\circ$

14. $19.6236^\circ$

15. $34.2367^\circ$

Перехід від десяткових градусів до DMS є більш складним процесом.

Перетворення з десяткових градусів в DMS

1. Вся числова частина вимірювання кута дає кількість градусів.
2. Помножте десяткову частину на$60$. Вся числова частина цього результату - це кількість хвилин.
3. Помножте десяткову частину хвилин на$60$. Це дає кількість секунд (включаючи будь-яку десяткову частину секунд).

Наприклад, давайте конвертуємо$15.374^\circ$.

1. Ступені частиною нашої відповіді будуть$15$.
2. Десяткова частина$60$ -$0.374\cdot60=22.44$ хвилини. Хвилинна частина нашої відповіді буде$22$.
3. Десяткова частина$60$ -$0.44\cdot60=26.4$ секунди. Секундна частина нашої відповіді буде$26.4$.

Отже$15.374^\circ=15^\circ22'26.4''$.

Вправи$\PageIndex{1}$

Перетворіть кожне вимірювання кута з десяткового в градуси-хвилин-секунди форми.

16. $26.785^\circ$

17. $58.216^\circ$

18. $41.13^\circ$

Відповідь

16. $26^\circ47'6''$

17. $58^\circ12'57.6''$

18. $41^\circ7'48''$

---

1. Ми округляємо до чотирьох знаків після коми, тому що$1$ другий кут дорівнює$\dfrac{1}{3,600}$ градусу. Це менша частка, ніж$\dfrac{1}{1,000}$ так наша точність трохи краще, ніж тисячне місце. ⦁