Skip to main content
LibreTexts - Ukrayinska

1.18: Трикутники

  1. Last updated
  2. Save as PDF
  • Page ID
    65829

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    За потреби ви можете використовувати калькулятор у цьому модулі.

    Класифікація трикутників

    Ми можемо класифікувати трикутники на три категорії на основі довжини їх сторін.

    • Рівносторонній трикутник: всі три сторони мають однакову довжину
    • Рівнобедрений трикутник: рівно дві сторони мають однакову довжину
    • Скальний трикутник: всі три сторони мають різну довжину

    Ми також можемо класифікувати трикутники на три категорії на основі мір їх кутів.

    • Тупий трикутник: один з кутів - тупий кут
    • Прямокутний трикутник: один з кутів - прямий кут
    • Гострий трикутник: всі три кути гострі
    Вправи\(\PageIndex{1}\)

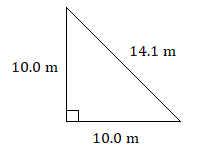
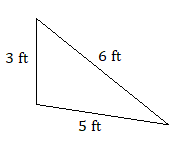
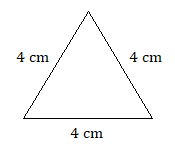
    Класифікуйте кожен трикутник за кутом і стороною. Наприклад, «гостра шкала».)

    1.

    2.

    3.

    Відповідь

    1. правий рівнобедрений трикутник

    2. тупий сходовий трикутник

    3. гострий рівносторонній трикутник (так, рівносторонній трикутник завжди буде гострим)

    Подібні трикутники

    На одній з діаграм попереднього модуля паралельні лінії включали два аналогічних трикутника, хоча їх може бути важко розгледіти.

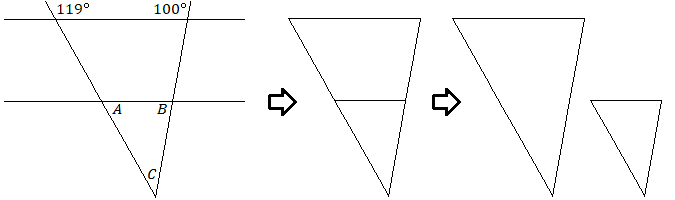
    Два трикутника схожі, якщо три кути одного трикутника мають таку ж міру, як і три кути другого трикутника. Довжини сторін аналогічних трикутників будуть в однаковій пропорції. Трикутники матимуть однакову форму, але довжини будуть масштабовані вгору або вниз.

    Вправи\(\PageIndex{1}\)

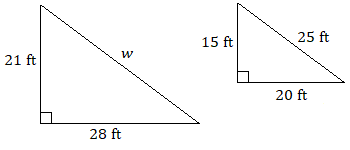
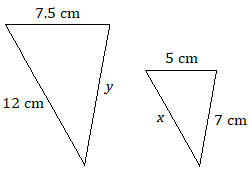
    Припустимо, що кожна пара трикутників схожа. Використовуйте пропорцію, щоб знайти кожну невідому довжину.

    4.

    5.

    Відповідь

    4. \(w=35\text{ ft}\)

    5. \(x=8\text{ cm}\);\(y=10.5\text{ cm}\)

    Розпізнати відповідні сторони може бути складніше, коли фігури орієнтовані по-різному.

    Вправи\(\PageIndex{1}\)

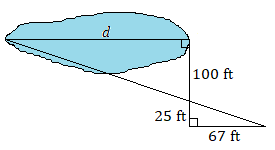
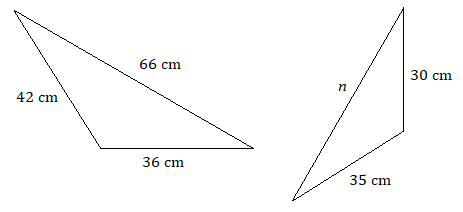
    Припустимо, що кожна пара трикутників схожа. Використовуйте пропорцію, щоб знайти кожну невідому довжину.

    6.

    7. аналогічні трикутники: один зі сторонами 42 см, 66 см, 36 см; інший зі сторонами n, 30 см, 35 см.

    Відповідь

    6. \(d=268\text{ ft}\)

    7. \(n=55\text{ cm}\)

    Прямі трикутники

    У прямокутному трикутнику дві сторони, що утворюють прямий кут, називаються ніжками. Сторона, протилежна прямому куту, яка завжди буде найдовшою стороною, називається гіпотенузою.

    Теорема Піфагора говорить, що сума квадратів довжин катетів дорівнює квадрату довжини гіпотенузи.

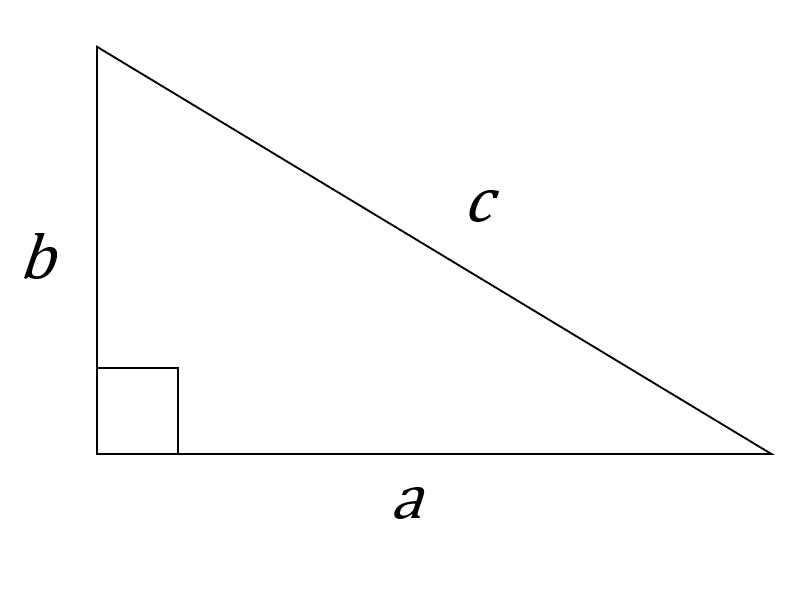
    Теорема\(\PageIndex{1}\): The Pythagorean Theorem

    У прямокутному трикутнику з\(a\) катетами\(b\) і і\(c\) гіпотенузою

    \[a^2+b^2=c^2 \nonumber \]

    Якщо ви знаєте довжини всіх трьох сторін трикутника, ви можете використовувати теорему Піфагора, щоб перевірити, чи є трикутник прямокутним трикутником чи ні. Стародавні єгиптяни використовували цей метод для геодезії, коли їм потрібно було перекреслити межі після щорічного затоплення Нілу змили їх попередню розмітку. [1]

    Вправи\(\PageIndex{1}\)

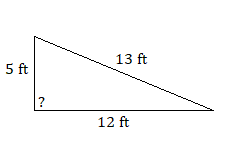
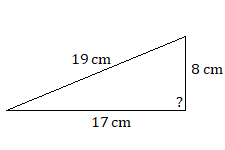
    Використовуйте теорему Піфагора, щоб визначити, чи є будь-який з наступних трикутників прямокутним трикутником.

    8.

    9.

    Відповідь

    8. прямокутний трикутник, тому що\(5^2+12^2=13^2\)

    9. не прямокутний трикутник, тому що\(8^2+17^2\neq19^2\)

    Перш ніж продовжити, потрібно коротко обговорити квадратні коріння. Обчислення квадратного кореня протилежне квадратичному числу. Наприклад,\(\sqrt{49}=7\) тому що\(7^2=49\). Якщо число під символом квадратного кореня не є ідеальним квадратом\(49\), як, то квадратний корінь буде ірраціональною десятковою комою, яку ми будемо округлити в міру необхідності.

    Вправи\(\PageIndex{1}\)

    Використовуйте калькулятор, щоб знайти значення кожного квадратного кореня. Округлити до сотих місць.

    10. \(\sqrt{50}\)

    11. \(\sqrt{296}\)

    12. \(\sqrt{943}\)

    Відповідь

    10. \(7.07\)

    11. \(17.20\)

    12. \(30.71\)

    Ми найчастіше використовуємо теорему Піфагора для обчислення довжини відсутньої сторони прямокутного трикутника. Ось три різні версії теореми Піфагора, організовані для пошуку відсутньої сторони, тому вам не доведеться використовувати алгебру з\(a^2+b^2=c^2\).

    Теорема Піфагора, три інші версії

    \(c=\sqrt{a^2+b^2}\)

    \(b=\sqrt{c^2-a^2}\)

    \(a=\sqrt{c^2-b^2}\)

    Вправи\(\PageIndex{1}\)

    Знайдіть довжину відсутньої сторони для кожного з цих правильних трикутників. Округлити до найближчої десятої, якщо це необхідно.

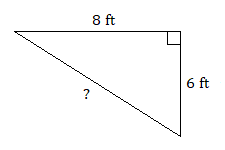
    13.

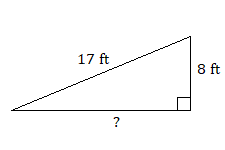
    14.

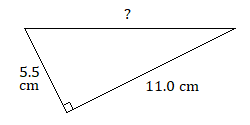
    15.

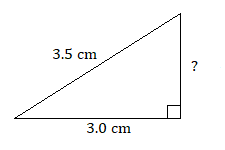
    16.

    Відповідь

    13. \(10\text{ ft}\)

    14. \(15\text{ ft}\)

    15. \(12.3\text{ cm}\)

    16. \(1.8\text{ cm}\)

    1. Геодезисти називали «мотузки-носилки», оскільки вони використовували петлю з\(12\) мотузкових одиниць довжиною з\(12\) рівнорозміщеними вузлами. Три мотузки-носилки кожен тримали вузол, утворюючи трикутник з відрізками\(3\)\(4\), і\(5\) одиницями. Коли мотузка була натягнута щільно, вони знали, що кут між сторонами\(3\) -одиниці та\(4\) -одиниці був прямим кутом, тому що\(3^2+4^2=5^2\). З відкриття геометрії: індуктивний підхід Майкла Серра, Клавіша Навчальна преса, 1997. ←