1.4: Паралельні лінії
- Page ID
- 58802
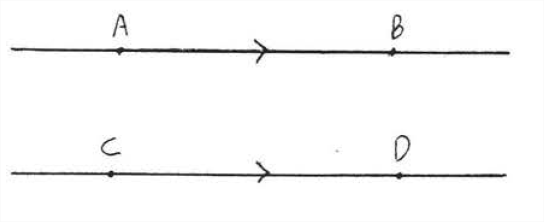
Дві лінії паралельні, якщо вони не зустрічаються, незалежно від того, наскільки вони протягнуті. Символ паралелі є\(||\). На малюнку\(\PageIndex{1}\),\(\stackrel{\leftrightarrow}{A B}\)\(||\)\(\stackrel{\leftrightarrow}{C D}\). Позначки стрілок використовуються для позначення паралельних ліній.
Робимо наступне припущення про паралельних лініях, званих паралельним постулатом.
Імовірності, присвоєні подіям функцією розподілу на вибірковому просторі, задаються
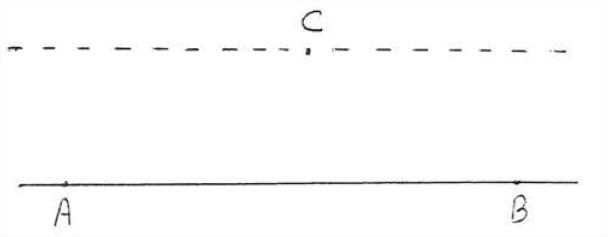
Через точку не на заданій прямій можна провести одну і тільки одну лінію паралельно заданій лінії. Таким чином\(\PageIndex{3}\), на малюнку, є точно одна лінія, яка може бути проведена через\(C\) що паралельно\(\overleftarrow{\mathrm{AB}}\).
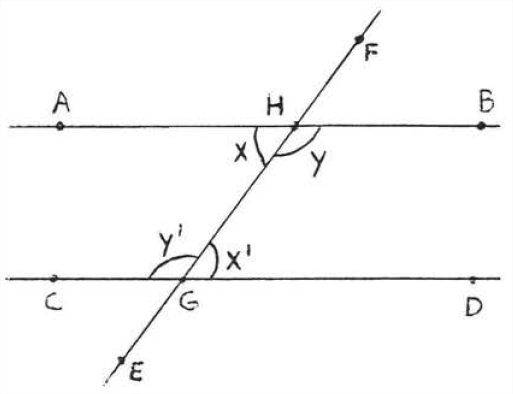
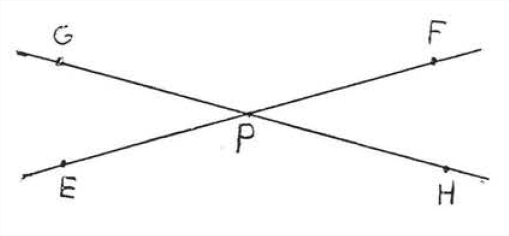
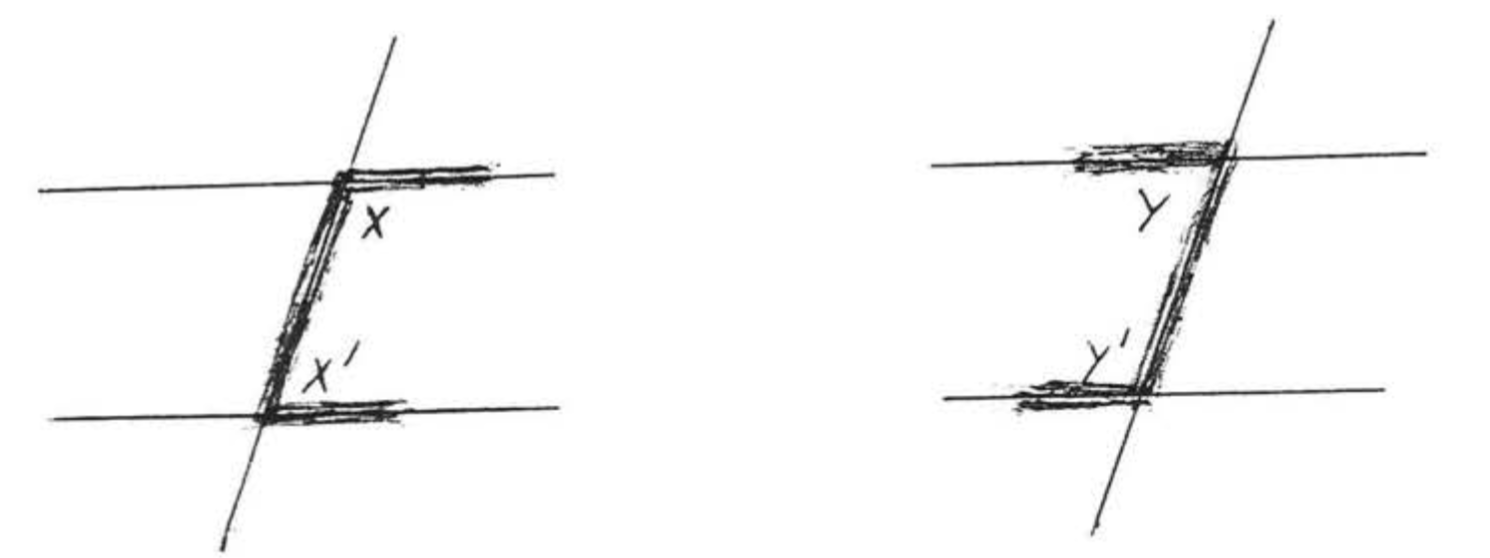
Поперечна - це лінія, яка перетинає дві інші лінії в двох різних точках. На малюнку\(\PageIndex{4}\),\(\overleftrightarrow{EF}\) є поперечним. \(\angle x\)і\(\angle x^{\prime}\) називаються чергуються внутрішні кути ліній\(\overleftrightarrow{AB}\) і\(\overleftrightarrow{CD}\). Слово «чергувати» тут означає, що кути знаходяться з різних сторін поперечного, один кут утворений з,\(\overleftrightarrow{AB}\) а інший утворений с\(\overleftrightarrow{CD}\). Слово «інтер'єр» означає, що вони знаходяться між двома рядками. Зверніть увагу, що вони утворюють букву "»\(Z\). (Малюнок\(\PageIndex{5}\)). \(\angle y\)а\(\angle y^{\prime}\) також чергуються внутрішні кути. Вони також утворюють\(Z\) "" хоча Він розтягується і назад. Якщо дивитися збоку, буква\(Z\) "" також може виглядати як «»\(N\).
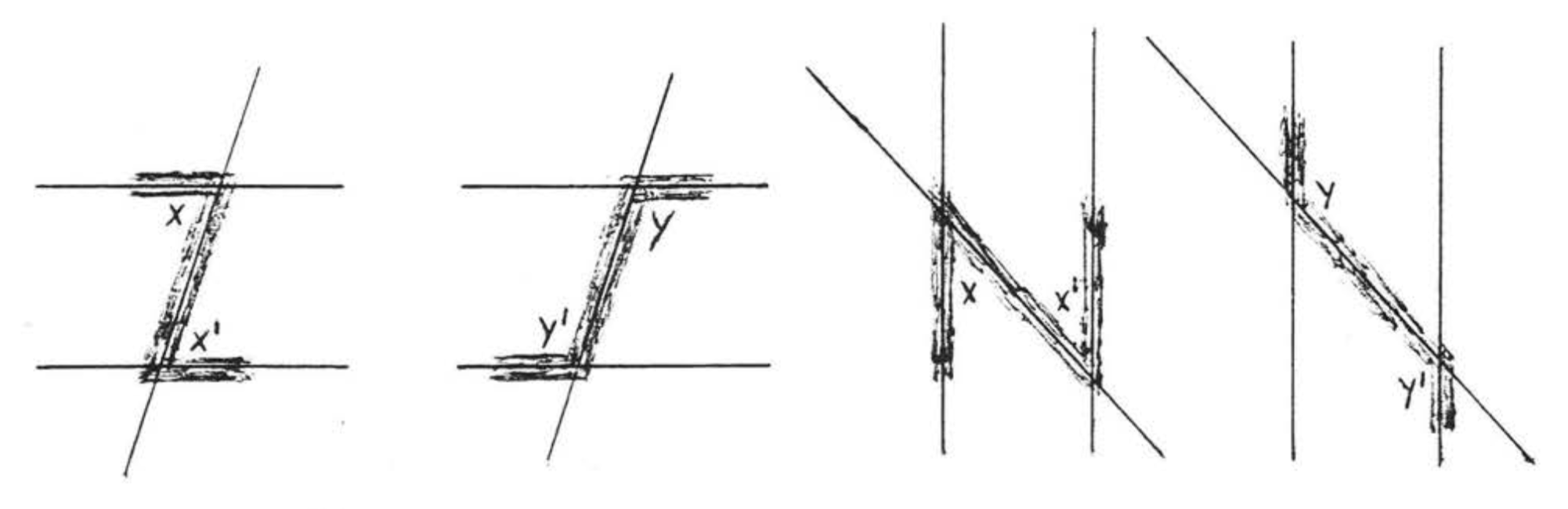
Альтернативні внутрішні кути важливі через наступну теорему:
Якщо дві лінії паралельні, то їх альтернативні внутрішні кути рівні, Якщо альтернативні внутрішні кути двох ліній рівні, то лінії повинні 'або паралельно,
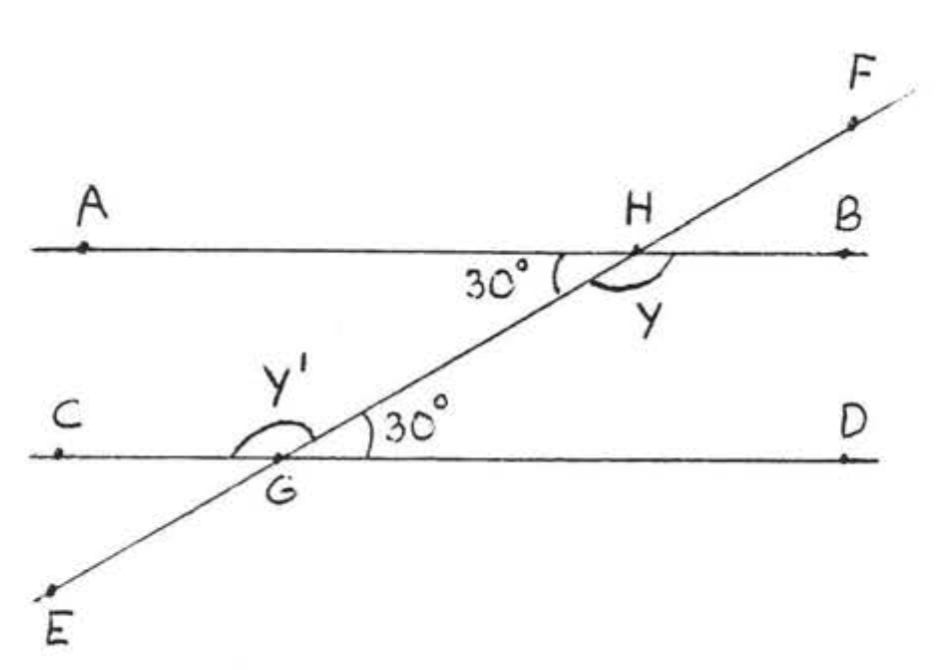
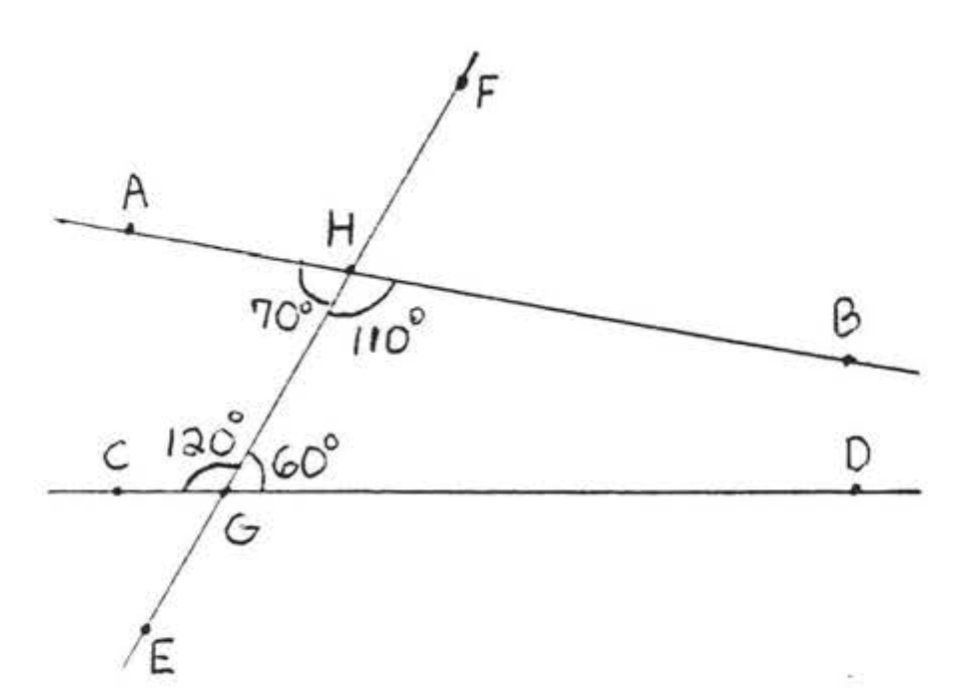
На малюнку\(\PageIndex{6}\),\(\overleftrightarrow{AB}\) повинні бути паралельні\(\overleftrightarrow{CD}\) тому, що чергуються внутрішні кути обидва\(30^{\circ}\). Зверніть увагу, що інші пари чергуються внутрішні кути\(\angle y'\),\(\angle y\) і, також рівні. Вони обидва\(150^{\circ}\). На\(\PageIndex{7}\) малюнку лінії не паралельні і жоден з альтернативних внутрішніх кутів не рівні.
Доказ теореми\(\PageIndex{1}\) є складним і буде перенесено на додаток.
Знайти\(x, y\) і\(z\):
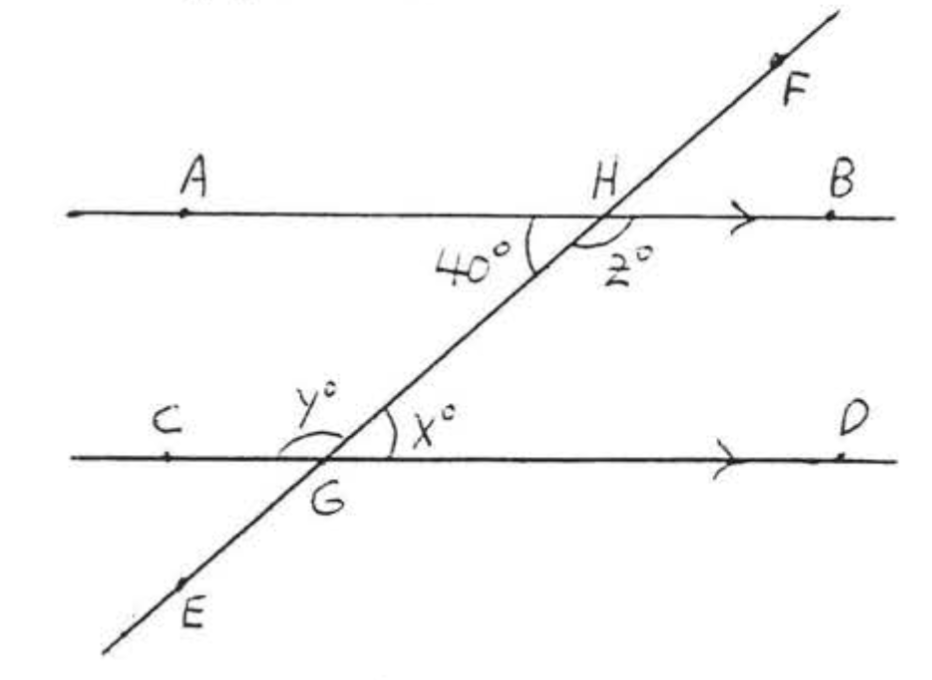
Рішення
\(\overleftrightarrow{AB} || \overleftrightarrow{CD}\)так як стрілки позначають паралельні лінії. \(x^{\circ} = 40^{\circ}\)тому що поперемінні внутрішні кути паралельних ліній рівні. \(y^{\circ} = z^{\circ} = 180^{\circ} - 40^{\circ} = 140^{\circ}\).
Відповідь:\(x = 40, y = 140, z = 140\).
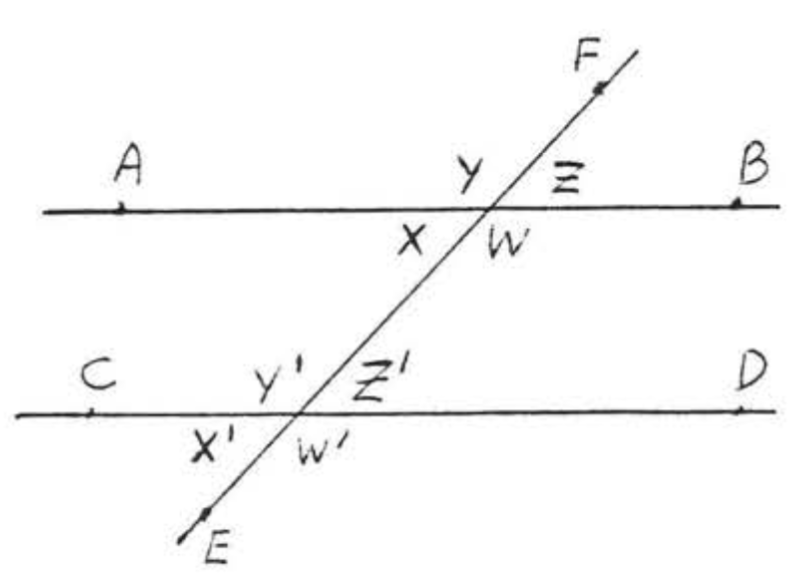
Відповідні кути двох ліній - це два кути, які знаходяться на одній стороні двох ліній і однаковій стороні поперечної, На малюнку\(\PageIndex{8}\),\(\angle w\) і\(\angle w'\) є відповідними кутами ліній\(\overleftrightarrow{AB}\) і\(\overleftrightarrow{CD}\). Вони утворюють букву «»\(F\). \(\angle x\)і\(\angle x'\),\(\angle y\) і\(\angle y'\),\(\angle z\) і\(\angle z'\) є іншими парами відповідних кутів\(\overleftrightarrow{AB}\) і\(\overleftrightarrow{CD}\). Всі вони утворюють букву "\(F\)«, хоча це може бути «назад або догори ногами\(F\)» (рис.\(\PageIndex{9}\)).
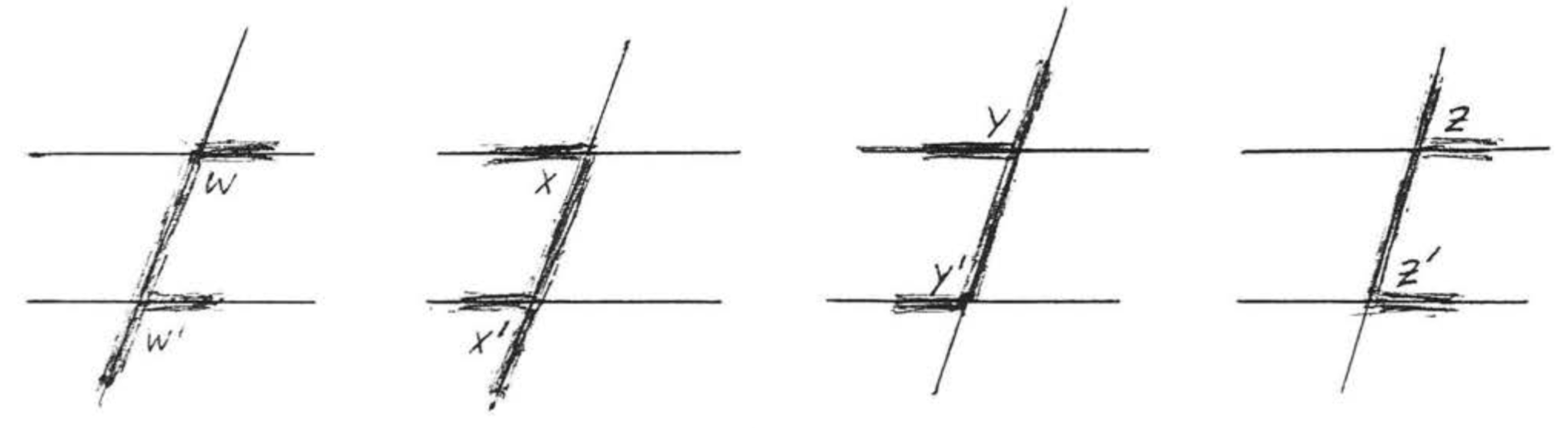
Відповідні кути важливі через наступну теорему:
Якщо дві лінії паралельні, то відповідні їм кути рівні. Якщо відповідні кути двох ліній рівні, то лінії повинні бути паралельними.
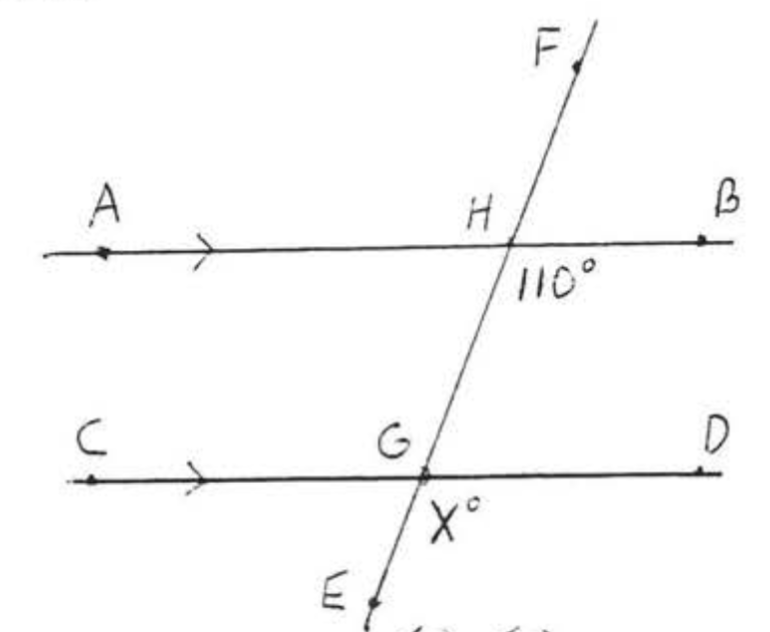
Знайти\(x\):
Рішення
Стрілкою вказується\(\overleftrightarrow{AB} || \overleftrightarrow{CD}\). Тому\(x^{\circ} = 110^{\circ}\) тому що\(x^{\circ}\) і\(110^{\circ}\) є мірами відповідних кутів паралельних ліній\(\overleftrightarrow{AB}\) і\(\overleftrightarrow{CD}\).
Відповідь:\(x = 110\).
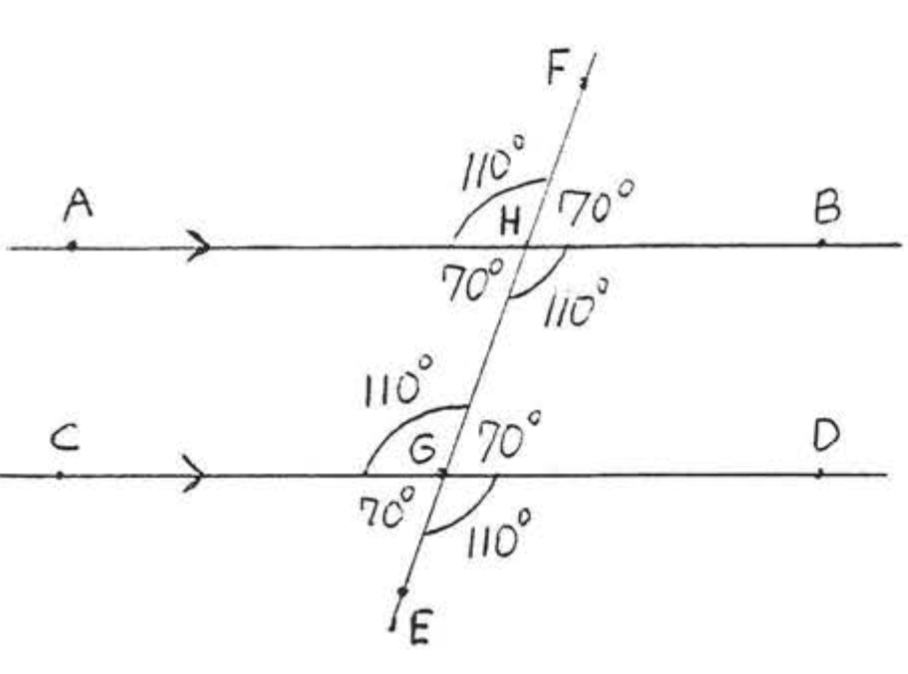
Зверніть увагу, що тепер ми можемо знайти всі інші кути в прикладі\(PageIndex{2}\). Кожен з них є або додатковим до одного з\(110^{\circ}\) кутів, або утворює рівні вертикальні кути з одним з них (рис.\(PageIndex{10}\)). Тому всі відповідні кути рівні, також кожна пара чергуються внутрішніх кутів дорівнює. Неважко помітити, що якщо тільки одна пара відповідних кутів або одна пара альтернативних внутрішніх кутів рівні, то так само і всі інші пари відповідних і альтернативних внутрішніх кутів.
Доказ теореми\(\PageIndex{2}\): Відповідні кути будуть рівними, якщо альтернативні внутрішні кути рівні і навпаки. Тому теорема\(\PageIndex{2}\) випливає безпосередньо з Теорема\(\PageIndex{1}\).
На\(\PageIndex{11}\) малюнку\(\angle x\) і\(\angle x'\) називаються внутрішні кути з тієї ж сторони поперечного. (У деяких підручниках внутрішні кути на одній стороні поперечного називають кутами співвісника.) \(\angle y\)а також внутрішні кути на тій же стороні поперечного, Зверніть увагу, що кожна пара кутів утворює букву "»\(C\).\(\angle y'\) Порівняйте рисунок\(\PageIndex{11}\) з малюнком 10, а також з прикладом\(\PageIndex{1}\), Потім очевидна наступна теорема:
Якщо дві лінії паралельні, то внутрішні кути на тій же стороні поперечного є додатковими (вони складають Up до\(180^{\circ}\)). Якщо внутрішні кути двох ліній на одній стороні поперечного є додатковими, то лінії повинні бути паралельними.
Знайдіть\(x\) і позначені кути:
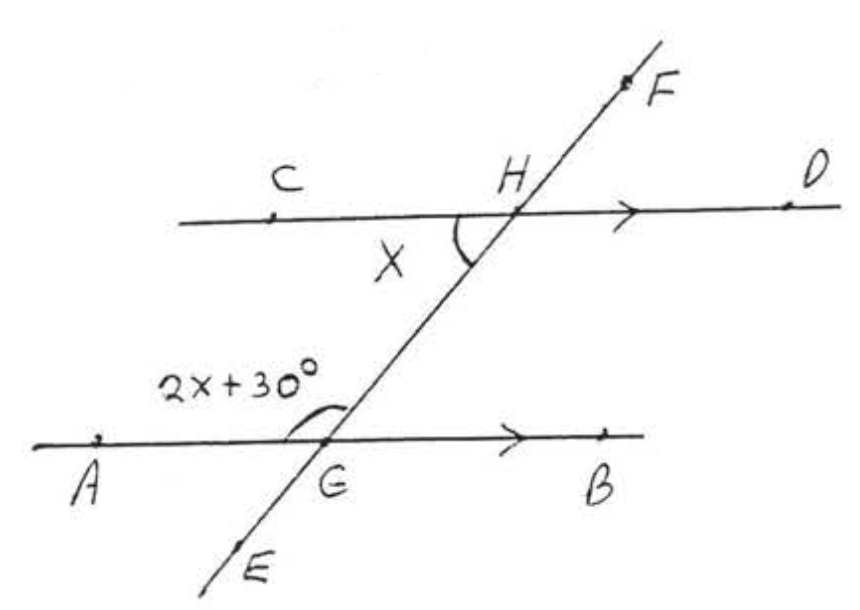
Рішення
Лінії паралельні, так по теоремі\(\PageIndex{3}\) the two labelled angles must be supplementary.
\[\begin{array} {rcl} {x + 2x + 30} & = & {180} \\ {3x + 30} & = & {180} \\ {3x} & = & {180 - 30} \\ {3x} & = & {150} \\ {x} & = & {50} \end{array}\]
\(\angle CHG = x = 50^{\circ}\)
\(\angle AGH = 2x + 30 = 2(50) + 30 = 100 + 30 = 130^{\circ}\).
Перевірка:
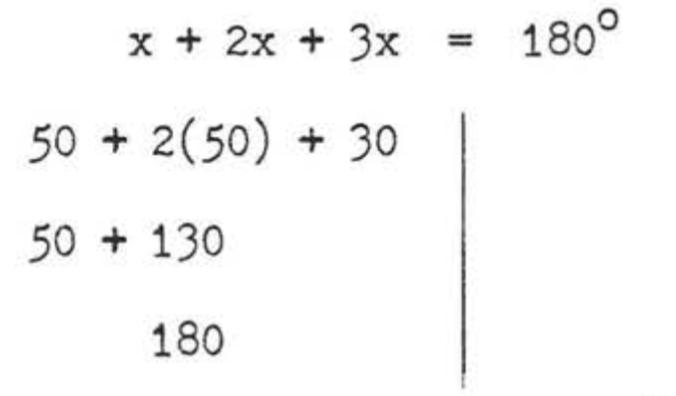
Відповідь:\(x = 50\),\(\angle CHG = 50^{\circ}\),\(\angle AGHa = 130^{\circ}\).
Знайдіть\(x\) і позначені кути:
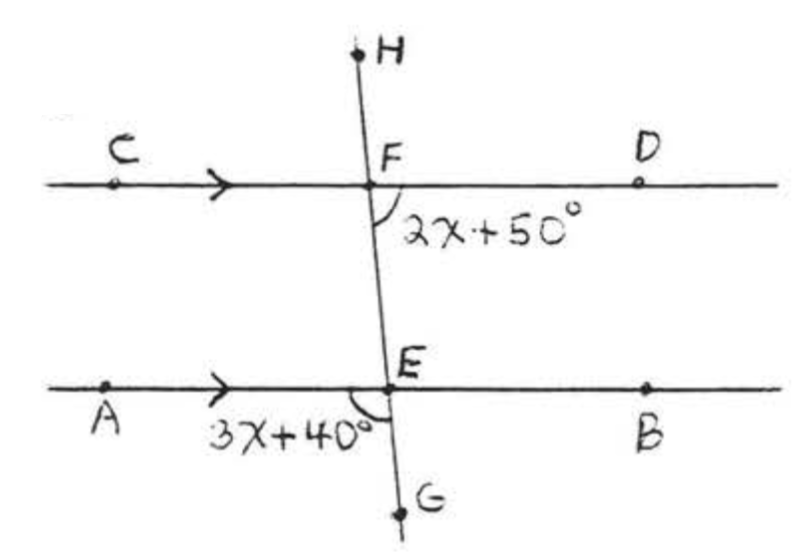
Рішення
\(\angle BEF = 3x + 40^{\circ}\)тому що вертикальні кути рівні. \(\angle BEF\)і\(\angle DFE\) є внутрішніми кутами на тій же стороні поперечного, і тому є додатковими, оскільки лінії паралельні.
\[\begin{array} {rcl} {3x + 40 + 2x + 50} & = & {180} \\ {5x + 90} & = & {180} \\ {5x} & = & {180 - 90} \\ {5x} & = & {90} \\ {x} & = & {18} \end{array}\]
\(\angle AEC = 3x + 40 = 3(18) + 40 = 54 + 40 = 94^{\circ}\)
\(\angle DFE = 2x + 50 = 2(18) + 50 = 36 + 50 = 86^{\circ}\)
Перевірка:
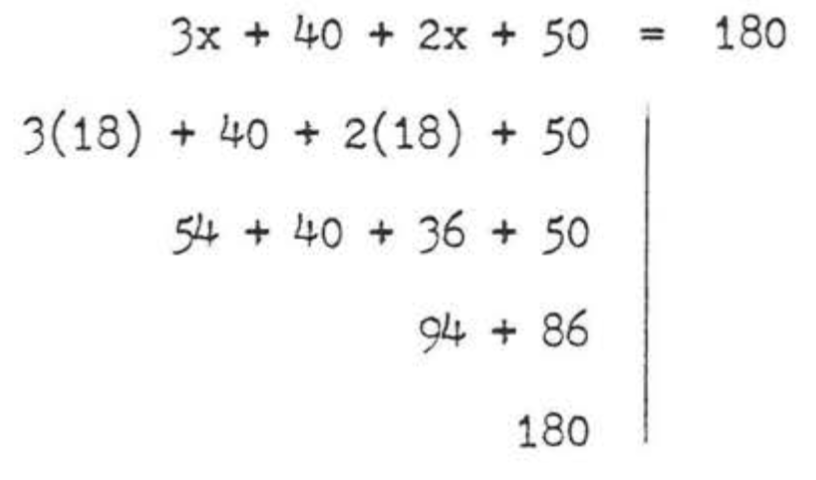
Відповідь:\(x = 18\),\(\angle AEG = 94^{\circ}\),\(\angle DFE = 86^{\circ}\).
Перерахуйте всі пари альтернативних внутрішніх кутів на діаграмі, (Одинарна стрілка вказує\(\overleftrightarrow{AB}\) паралельно,\(\overleftrightarrow{CD}\) а подвійна стрілка вказує\(\overleftrightarrow{AD}\) паралельно\(\overleftrightarrow{BC}\).

Рішення
Бачимо,\(Z\) чи\(N\) може бути утворена буква або за допомогою відрізків лінії на схемі (рис.\(\PageIndex{12}\)),
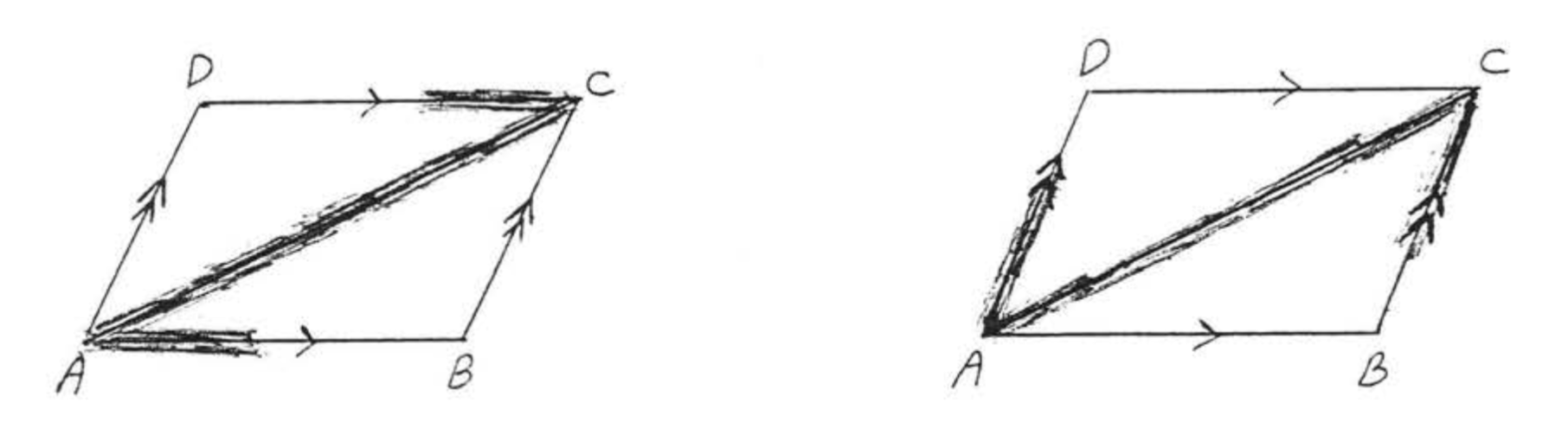
Відповідь:\(\angle DCA\) і\(\angle CAB\) чергуються внутрішні кути ліній\(\overleftrightarrow{AB}\) і\(\overleftrightarrow{CD}\). \(\angle DAC\)і\(\angle ACB\) чергуються внутрішні кути ліній\(\overleftrightarrow{AD}\) і\(\overleftrightarrow{BC}\)
Телескоп спрямований на зірку\(70^{\circ}\) над горизонтом, Який кут\(x^{\circ}\) має\(BD\) зробити дзеркало з горизонталлю, щоб зірку можна було побачити в окулярі\(E\)?
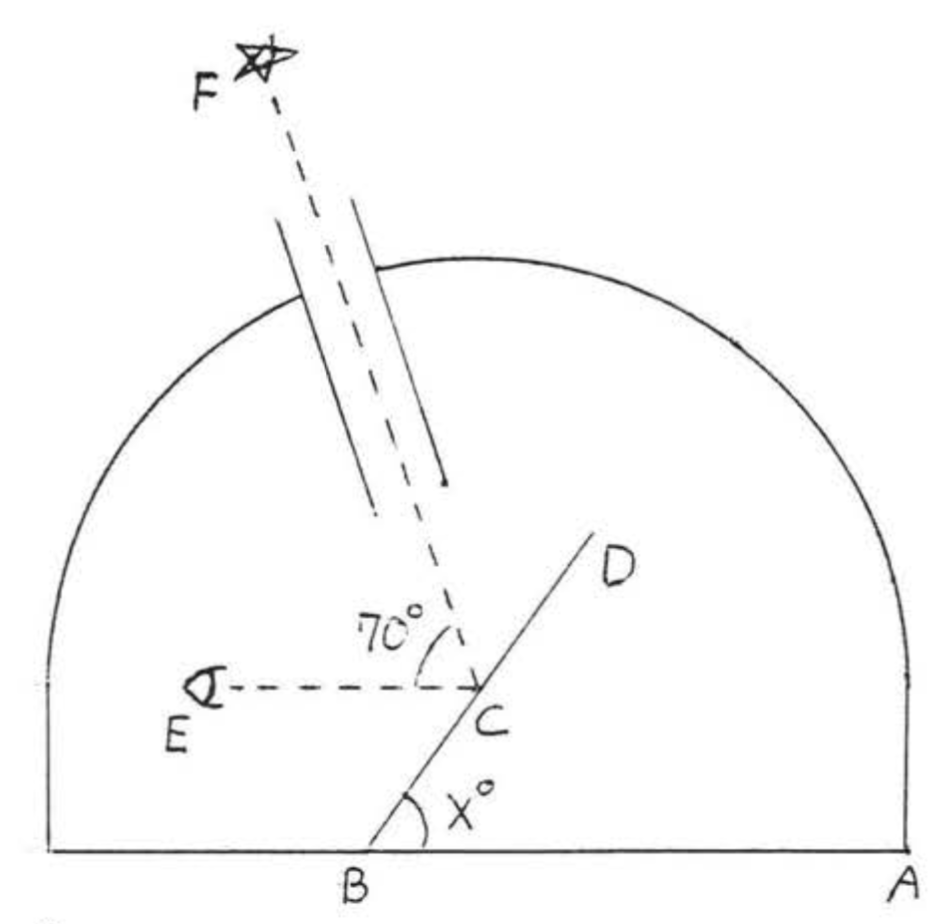
Рішення
\(x^{\circ} = \angle BCE\)тому що вони чергуються внутрішніми кутами паралельних ліній\(\overleftrightarrow{AB}\) і\(\overleftrightarrow{CE}\). \(\angle DCF = \angle BCE = x^{\circ}\)тому що кут падіння дорівнює куту відбиття. Тому
\[\begin{array} {rcl} {x + 70 + x} & = & {180} \\ {2x + 70} & = & {180} \\ {2x} & = & {110} \\ {x} & = & {55} \end{array}\]
Відповідь:\(55^{\circ}\)
РЕЗЮМЕ

Чергуються внутрішні кути паралельних ліній рівні. Вони утворюють букву «»\(Z\).
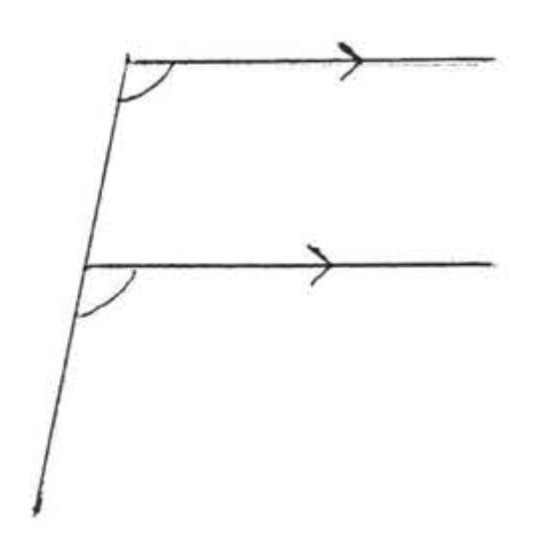
Відповідні кути паралельних ліній рівні. Вони утворюють букву «»\(F\).
Внутрішні кути з тих же сторін поперечних паралельних ліній є додатковими. Вони утворюють букву «»\(G\).
Паралельний постулат, наведений раніше в цьому розділі, є еквівалентом п'ятого постулату Стихій Евкліда. Евклід був правильний, припускаючи це як постулат, а не намагався довести це як теорему, Однак це не стало зрозуміло математичному світу до дев'ятнадцятого століття, 2200 років потому, У проміжний час, десятки видатних математиків безуспішно намагалися дати задовільний доказ паралельний постулат. Вони вважали, що це не так само собою зрозуміло, як повинен бути постулат, і що це вимагає певного формального обґрунтування,
У 1826 р Н, І, Лобачевський, російський математик, представив систему геометрії, засновану на припущенні, що через задану точку паралельно заданій лінії можна провести більше однієї прямої (рис.\(\PageIndex{13}\)). У 1854 році німецький математик Георг Бернхард Ріман проформував систему Geometrij, в якій паралельних ліній взагалі немає, А геометрія, в якій паралельний постулат був замінений якимось іншим постулатом, називається неевклідової геометрією. Існування цих геометрій показує, що паралельний постулат не обов'язково повинен бути істинним. Дійсно, Ейнштейн використовував геометрію Рімана як основу своєї теорії відносності.

Звичайно, наш оригінальний паралельний постулат має найбільш сенс для звичайних додатків, і ми використовуємо його протягом цієї книги, Однак, для додатків, де задіяні великі відстані, наприклад, в астрономії, цілком може бути, що неевклідова геометрія дає краще наближення фізичної реальності.
Проблеми
Для кожного з наступного вкажіть теорему (и), використану при отриманні вашої відповіді (наприклад, «альтернативні внутрішні кути паралельних ліній рівні»). Лінії, позначені тією ж стрілкою, приймаються паралельними,
1 - 2. Знайти\(x, y\), і\(z\):
1.  2.
2. 
3 - 4. Знайти\(t\),\(u\),\(v\),\(w\),\(x\),\(y\), і\(z\):
3.  4.
4. 
5 - 10. Знайти\(x\):
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 
11 - 18. Знайдіть\(x\) і позначені кути:
11.  12.
12. 
13.  14.
14. 
15.  16.
16. 
17.  18.
18. 
19 - 26. Для кожного з наступних перерахуйте всі пари чергуються внутрішніх кутів і відповідних кутів, Якщо таких немає, то перерахуйте всі пари внутрішніх кутів на тій же стороні поперечного. Вкажіть паралельні лінії, які утворюють кожну пару кутів.
19.  20.
20. 
21.  22.
22. 
23. 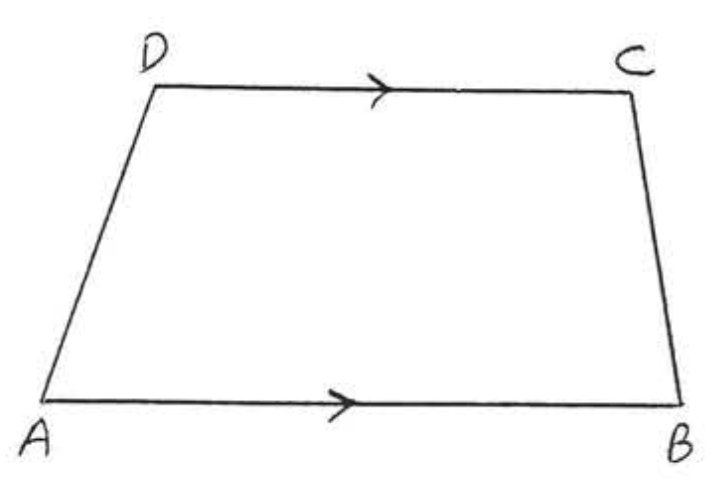 24.
24. 
25.  26.
26. 
27. Телескоп спрямований на зірку\(50^{\circ}\) над горизонтом. Який кут\(x^{\circ}\) має\(BD\) зробити дзеркало з горизонталлю, щоб зірку можна було побачити в окулярі\(E\)?

28. Перископ використовується моряками в підводному човні, щоб побачити предмети на поверхні води, Якщо\(\angle ECF = 90^{\circ}\), який кут\(x^{\circ}\)\(BD\) робить дзеркало з горизонтальним?

