7.5: Суми та відмінності раціональних функцій

У цьому розділі ми зосередимося на пошуку сум і відмінностей раціональних виразів. Однак, перш ніж ми почнемо, нам потрібно переглянути деякі фундаментальні ідеї та техніку.

В першу чергу це поняття кратне цілого числа. Найкраще це пояснити на простому прикладі. Кратні 8 - це множина цілих чисел$\{8 k : k \text { is an integer }\}$. Іншими словами, якщо ви помножите 8 на$0, \pm 1, \pm 2, \pm 3, \pm 4$ і т.д., ви виробляєте те, що відомо як кратні 8.

$$\text { Multiples of } 8 \text { are: } 0, \pm 8, \pm 16, \pm 24, \pm 32, \text { etc. }$$

Однак для наших цілей інтерес представляють тільки позитивні кратні. Отже, скажемо:

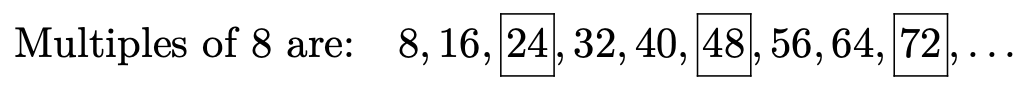
Аналогічно, ми можемо перерахувати позитивні кратні 6.

Ми обрамляли ті числа, які кратні як 8, так і 6. Вони називаються загальними кратними 8 і 6.

$$\text { Common multiples of } 8 \text { and } 6 \text { are: } 24,48,72, \ldots$$

Найменший з цього списку спільних кратних 8 і 6 називається найменш загальним кратним 8 і 6. Ми будемо використовувати наступні позначення, щоб представити найменш поширене кратне 8 і 6: LCM (8, 6).

Сподіваємось, тепер ви будете почувати себе комфортно з наступним визначенням.

Визначення: Найменш поширене кратне (LCM)

$b$Дозволяти$a$ і бути цілими числами. Найменше спільне кратне a і b, що позначається LCM (a, b), є найменшим додатним кратним, що a і b мають спільне.

Для більших чисел перерахування кратних, поки ви не знайдете один спільного, може бути непрактичним і трудомістким. Давайте знайдемо найменш поширене кратне 8 і 6 вдруге, тільки цього разу давайте використаємо іншу техніку.

Спочатку запишіть кожне число як добуток простих чисел в експоненціальній формі.

$$\begin{array}{l}{8=2^{3}} \\ {6=2 \cdot 3}\end{array}$$

Ось правило.

Процедура пошуку LCM

Щоб знайти НСК двох цілих чисел, дійте наступним чином.

1. Висловіть просту факторизацію кожного цілого числа в експоненціальному форматі.
2. Щоб знайти найменш поширене кратне, запишіть кожне просте число, яке з'являється, а потім прикріпіть найбільший показник цього простого, що з'являється.

У нашому прикладі прості числа, які зустрічаються, - це 2 і 3. Найвища потужність 2, що відбувається, є$2^{3}$. Найвища потужність 3, що відбувається, є$3^{1}$. Таким чином, НСМ (8, 6) - це

$$\operatorname{LCM}(8,6)=2^{3} \cdot 3^{1}=24$$

Зауважте, що цей результат ідентичний результату, знайденому вище, шляхом перерахування всіх загальних кратних і вибору найменшого.

Давайте спробуємо більш складний приклад.

Приклад$\PageIndex{1}$

Знайдіть найменш поширене кратне 24 і 36.

Рішення

Використовуючи перший прийом, перерахуємо кратні кожному числу, обрамляючи кратні спільними.

Спільними кратними є 72, 144 тощо, а найменш загальним кратним є LCM (24, 36) = 72.

Тепер давайте використаємо нашу другу техніку, щоб знайти найменш поширене кратне (LCM). По-перше, висловіть кожне число як добуток простих чисел в експоненціальному форматі.

$$\begin{array}{l}{24=2^{3} \cdot 3} \\ {36=2^{2} \cdot 3^{2}}\end{array}$$

Щоб знайти найменш загальне кратне, запишіть кожне просте, що відбувається, і прикріпіть найвищу силу того простого, що відбувається. Таким чином, найвища потужність 2, що виникає$2^{3}$, і найвища потужність 3, що відбувається, є$3^{2}$. Таким чином, найменш поширеною кратної є $$\operatorname{LCM}(24,36)=2^{3} \cdot 3^{2}=8 \cdot 9=72$$

Визначено додавання та віднімання

Уявіть собі піцу, яку розрізали на 12 рівних скибочок. Потім кожен шматочок піци представляє 1/12 всієї піци.

Якщо Джиммі з'їдає 3 скибочки, значить, він спожив 3/12 всієї піци. Якщо Маргарет з'їдає 2 скибочки, значить, вона спожила 2/12 всієї піци. Зрозуміло, що разом вони споживали $$\frac{3}{12}+\frac{2}{12}=\frac{5}{12}$$

піци. Здавалося б, додавання двох дробів із загальним знаменником так само просто, як з'їсти піцу! Сподіваємося, наступне визначення здасться розумним.

Визначення

Щоб скласти два дроби із загальним знаменником, наприклад a/c і b/c, додайте чисельники і розділіть на спільний знаменник. В символах,

$$\frac{a}{c}+\frac{b}{c}=\frac{a+b}{c}$$

Зверніть увагу, як це визначення точно узгоджується з нашим споживанням піци, розглянутим вище. Ось кілька прикладів додавання дробів, що мають спільні знаменники.

$$\begin{array}{llllll} {\frac{5}{21}+\frac{3}{21}} & {=} & {\frac{5+3}{21}} & {\frac{2}{x+2}+\frac{x-3}{x+2}} & {=} & {\frac{2+(x-3)}{x+2}} \\{}& {=}&{\frac{8}{21}} & {} & {=}&{\frac{2+x-3}{x+2}} \\ {} &&&{}& {=}&{\frac{x-1}{x+2}}\end{array}$$

Віднімання працює приблизно так само, як і додавання.

Визначення

Для віднімання двох дробів із загальним знаменником, наприклад a/c і b/c, відніміть чисельники і діліть на загальний знаменник. В символах,

$$\frac{a}{c}-\frac{b}{c}=\frac{a-b}{c}$$

Ось кілька прикладів віднімання дробів, які вже мають спільні знаменники.

$$\begin{array}{llllll} {\frac{5}{21}-\frac{3}{21}} & {=} & {\frac{5-3}{21}} & {\frac{2}{x+2}-\frac{x-3}{x+2}} & {=} & {\frac{2-(x-3)}{x+2}} \\{}& {=}&{\frac{2}{21}} & {} & {=}&{\frac{2-x+3}{x+2}} \\ {} &&&{}& {=}&{\frac{5-x}{x+2}}\end{array}$$

У прикладі праворуч зверніть увагу, що вкрай важливо використовувати угруповання символів при відніманні чисельників. Зверніть увагу, що знак мінус перед дужковим виразом змінює знак кожного члена всередині дужок.

Бувають випадки, коли зміна знака забезпечить спільний знаменник.

Приклад$\PageIndex{2}$

Спростити $$\frac{x}{x-3}-\frac{2}{3-x}$$ державу всі обмеження.

Рішення

На перший погляд здається, що спільного знаменника у нас немає. На другий погляд, якщо ми зробимо зміну знака на другому дробі, це може допомогти. Отже, на другому дробі зведемо нанівець знаменник і бар дробу для отримання $$\frac{x}{x-3}-\frac{2}{3-x}=\frac{x}{x-3}+\frac{2}{x-3}=\frac{x+2}{x-3}$$

Знаменники x−3 або 3−x дорівнюють нулю, якщо x = 3. Отже, 3 є обмеженим значенням. Для всіх інших значень x лівою стороною

$$\frac{x}{x-3}-\frac{2}{3-x}=\frac{x+2}{x-3}$$

ідентична правій стороні.

Це легко перевірити за допомогою утиліти таблиць на графічному калькуляторі, як показано на послідовності скріншотів на малюнку$\PageIndex{1}$. Спочатку завантажте ліву та праву частини рівняння (7) у Y1 та Y2 у меню Y= вашого графічного калькулятора, як показано на малюнку$\PageIndex{1}$ (a). Натисніть 2nd TBLSET і внесіть зміни, показані на малюнку$\PageIndex{1}$ (b). Натисніть 2nd TABLE, щоб створити таблицю, показану на малюнку$\PageIndex{1}$ (c). Зверніть увагу на повідомлення ERR (помилка) при обмеженні x = 3, але зверніть увагу також на згоду Y1 і Y2 для всіх інших значень x.

Малюнок$\PageIndex{1}$. Використання функції таблиці графічного калькулятора для перевірки результату в рівнянні (7).

Еквівалентні дроби

Якщо ви нарізаєте піцу на чотири рівні частини, а потім споживаєте два з чотирьох скибочок, ви спожили половину піци. Це мотивує тим, що $$\frac{1}{2}=\frac{2}{4}$$ . Дійсно, якщо ви нарізаєте піцу на шість рівних шматочків, то споживаєте три скибочки, ви спожили половину піци, так що справедливо сказати, що 3/6 = 1/2. Дійсно, всі наступні дроби еквівалентні:

$$\frac{1}{2}=\frac{2}{4}=\frac{3}{6}=\frac{4}{8}=\frac{5}{10}=\frac{6}{12}=\frac{7}{14}=\cdots$$

Більш формальний спосіб продемонструвати, що 1/2 і 7/14 рівні - почати з того, що 1/2 = 1/2 × 1, потім замінити 1 на 7/7 і помножити.

$$\frac{1}{2}=\frac{1}{2} \times \color{blue}{1}=\frac{1}{2} \times \color{blue}{\frac{7}{7}}=\frac{7}{14}$$
Ось ще один приклад цього принципу в дії, тільки цього разу ми замінюємо 1 на (x − 2)/(x − 2).

$$\frac{3}{x+2}=\frac{3}{x+2} \cdot \color{blue}{1}=\frac{3}{x+2} \cdot \color{blue}{\frac{x-2}{x-2}}=\frac{3(x-2)}{(x+2)(x-2)}$$
У наступному прикладі ми замінюємо 1 на (x (x − 3))/(x (x − 3)).

$$\frac{2}{x-4}=\frac{2}{x-4} \cdot \color{blue}{1}=\frac{2}{x-4} \cdot \color{blue}{\frac{x(x-3)}{x(x-3)}}=\frac{2 x(x-3)}{x(x-4)(x-3)}$$
Тепер застосуємо поняття еквівалентних дробів для додавання та віднімання дробів з різними знаменниками.

Додавання та віднімання дробів з різними знаменниками

У цьому розділі ми покажемо нашим читачам, як додавати та віднімати дроби, що мають різні знаменники. Наприклад, припустимо, що нас попросять додати наступні дроби.

$$\frac{5}{12}+\frac{5}{18}$$

По-перше, ми повинні знайти «спільний знаменник». На щастя, техніка для пошуку «спільного знаменника» вже є на місці. Виходить, що найменш спільний знаменник для 12 і 18 - найменш спільний кратний 12 і 18.

$$\begin{aligned} 18 &=2 \cdot 3^{2} \\ 12 &=2^{2} \cdot 3 \\ \operatorname{LCD}(12,18) &=2^{2} \cdot 3^{2}=36 \end{aligned}$$

Наступним кроком є створення еквівалентних дробів, використовуючи РК-дисплей як знаменник. Так, у випадку з 5/12,

$$\frac{5}{12}=\frac{5}{12} \cdot \color{blue}{1}=\frac{5}{12} \cdot \color{blue}{\frac{3}{3}}=\frac{15}{36}$$
У випадку з 5/18 $$\frac{5}{18}=\frac{5}{18} \cdot \color{blue}{1}=\frac{5}{18} \cdot \color{blue}{\frac{2}{2}}=\frac{10}{36}$$

Якщо замінити дроби в рівнянні (8) на їх еквівалентні дроби, то можна додати чисельники і розділити на загальний знаменник, як у

$$\frac{5}{12}+\frac{5}{18}=\frac{15}{36}+\frac{10}{36}=\frac{15+10}{36}=\frac{25}{36}$$

Розберемо метод організації роботи, який є більш компактним. Розглянемо наступне розташування, де ми використали колір, щоб виділити форму 1, необхідну для перетворення дробів на еквівалентні дроби із загальним знаменником 36.

$$\begin{aligned} \frac{5}{12}+\frac{5}{18} &=\frac{5}{12} \cdot \color{blue}{\frac{3}{3}}+\frac{5}{18} \cdot \color{blue}{\frac{2}{2}} \\ &=\frac{15}{36}+\frac{10}{36} \\ &=\frac{25}{36} \end{aligned}$$
Давайте розглянемо більш складний приклад.

Приклад$\PageIndex{3}$

Спростити вираз $$\frac{x+3}{x+2}-\frac{x+2}{x+3}$$ State всі обмеження.

Рішення

Знаменники вже враховані. Якщо взяти кожен фактор, який здається найвищою експоненціальною потужністю, що з'являється, наш найменш спільний знаменник - (x+2) (x+3). Наше перше завдання - зробити еквівалентні дроби, що мають цей спільний знаменник.

$$\begin{aligned} \frac{x+3}{x+2}-\frac{x+2}{x+3} &=\frac{x+3}{x+2} \cdot \color{blue}{\frac{x+3}{x+3}}-\frac{x+2}{x+3} \cdot \color{blue}{\frac{x+2}{x+2}} \\ &=\frac{x^{2}+6 x+9}{(x+2)(x+3)}-\frac{x^{2}+4 x+4}{(x+2)(x+3)} \end{aligned}$$
Тепер віднімаємо чисельники і ділимо на спільний знаменник.

$$\begin{aligned} \frac{x+3}{x+2}-\frac{x+2}{x+3} &=\frac{\left(x^{2}+6 x+9\right)-\left(x^{2}+4 x+4\right)}{(x+2)(x+3)} \\ &=\frac{x^{2}+6 x+9-x^{2}-4 x-4}{(x+2)(x+3)} \\ &=\frac{2 x+5}{(x+2)(x+3)} \end{aligned}$$

Зверніть увагу на використання дужок, коли ми віднімали чисельники. Зверніть увагу далі, як знак мінус заперечує кожен член у дужковому виразі, що слідує за знаком мінус.

Чайові

Завжди використовуйте символи групування при відніманні чисельників дробів.

У остаточній відповіді множники x + 2 та x + 3 у знаменнику дорівнюють нулю, коли x = −2 або x = −3. Це обмеження. Ніякі інші знаменники, в початковій задачі або в тілі нашої роботи, не передбачають додаткових обмежень.

Таким чином, для всіх значень x, окрім обмежених значень −2 та −3, ліворуч

$$\frac{x+3}{x+2}-\frac{x+2}{x+3}=\frac{2 x+5}{(x+2)(x+3)}$$

ідентична правій стороні. Це твердження легко перевіряється на графічному калькуляторі, про що свідчить послідовність знімків екрану на малюнку$\PageIndex{2}$. Зверніть увагу на повідомлення ERR (помилка) при кожному обмеженому значенні x на малюнку$\PageIndex{2}$ (c), але також зверніть увагу на згоду Y1 та Y2 для всіх інших значень x.

Малюнок$\PageIndex{2}$. Використання функції таблиці графічного калькулятора для перевірки результату в рівнянні (12).

Давайте розглянемо інший приклад.

Приклад$\PageIndex{4}$

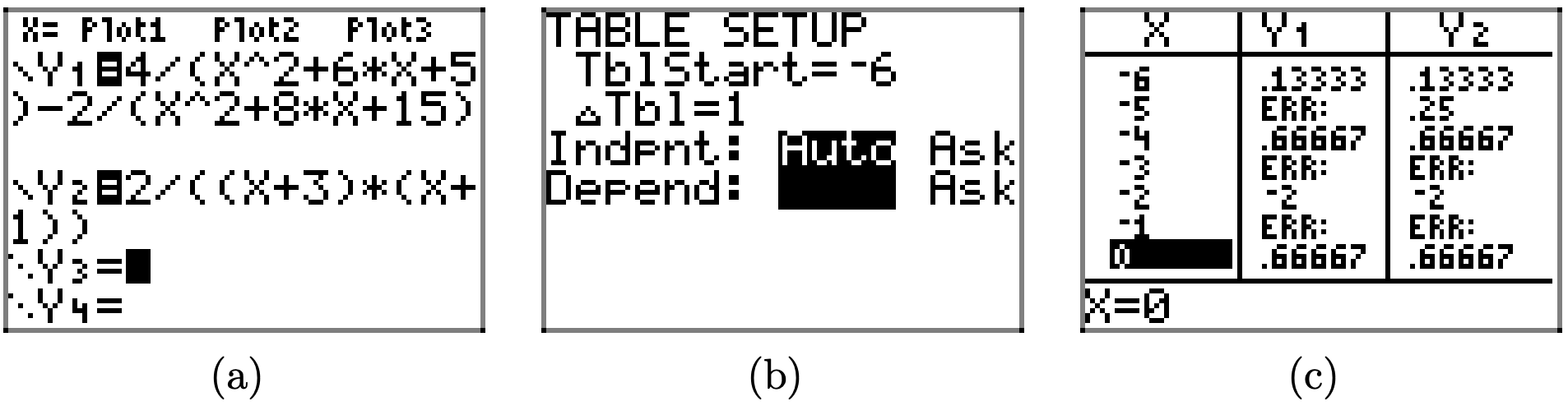
Спростити вираз $$\frac{4}{x^{2}+6 x+5}-\frac{2}{x^{2}+8 x+15}$$ . Вказати всі обмеження.

Рішення

По-перше, коефіцієнт кожного знаменника. $$\frac{4}{x^{2}+6 x+5}-\frac{2}{x^{2}+8 x+15}=\frac{4}{(x+1)(x+5)}-\frac{2}{(x+3)(x+5)}$$

Найменший спільний знаменник, або найменш спільний кратний (LCM), вимагає, щоб ми записували кожен фактор, який виникає, а потім закріплюємо найвищу потужність цього фактора, що виникає. Оскільки всі фактори в знаменниках піднімаються до зрозумілої потужності одного, РК-дисплей (найменш спільний знаменник) або LCM є (x + 1) (x + 5) (x + 3).

Далі робимо еквівалентні дроби, що мають цей спільний знаменник.

$$\begin{aligned} \frac{4}{x^{2}+6 x+5}-\frac{2}{x^{2}+8 x+15} &=\frac{4}{(x+1)(x+5)} \cdot \color{blue}{\frac{x+3}{x+3}}-\frac{2}{(x+3)(x+5)} \cdot \color{blue}{\frac{x+1}{x+1}} \\ &=\frac{4 x+12}{(x+3)(x+5)(x+1)}-\frac{2 x+2}{(x+3)(x+5)(x+1)} \end{aligned}$$
Віднімаємо чисельники і ділимо на спільний знаменник. Обов'язково використовуйте угруповання символів, особливо зі знаком мінус, який знаходиться в грі.

$$\begin{aligned} \frac{4}{x^{2}+6 x+5}-\frac{2}{x^{2}+8 x+15} &=\frac{(4 x+12)-(2 x+2)}{(x+3)(x+5)(x+1)} \\ &=\frac{4 x+12-2 x-2}{(x+3)(x+5)(x+1)} \\ &=\frac{2 x+10}{(x+3)(x+5)(x+1)} \end{aligned}$$

Нарешті, ми завжди повинні переконатися, що наша відповідь зводиться до найнижчих термінів. Маючи на увазі цю думку, ми враховуємо чисельник в надії, що ми зможемо отримати загальний коефіцієнт для скасування.

\[\begin{aligned} \frac{4}{x^{2}+6 x+5}-\frac{2}{x^{2}+8 x+15} &=\frac{2(x+5)}{(x+3)(x+5)(x+1)} \\ &=\frac{2(x+5)}{(x+3)(x+5)(x+1)} \\ &=\frac{2}{(x+3)(x+1)} \end{aligned}\]

Знаменники мають множники x+ 3, x+ 5 та x+ 1, тому обмеженнями є x = −3, x = −5 та x = −1 відповідно. Для всіх інших значень x лівою стороною

$$\frac{4}{x^{2}+6 x+5}-\frac{2}{x^{2}+8 x+15}=\frac{2}{(x+3)(x+1)}$$

ідентична його правій стороні. Знову ж таки, це легко перевіряється за допомогою функції таблиці графічного калькулятора, як показано на скріншотах на малюнку$\PageIndex{3}$. Знову ж таки, зверніть увагу на повідомлення ERR (помилки) при кожному обмеженому значенні x, але також зауважте, що Y1 і Y2 погоджуються для всіх інших значень x.

Малюнок$\PageIndex{3}$. Використання функції таблиці графічного калькулятора для перевірки результату в рівнянні (14).

Давайте розглянемо інший приклад.

Приклад$\PageIndex{5}$

Спростити вираз $$\frac{x-3}{x^{2}-1}+\frac{1}{x+1}-\frac{1}{1-x}$$ . Вказати всі обмеження.

Рішення

По-перше, розрахуйте всі знаменники.

$$\frac{x-3}{x^{2}-1}+\frac{1}{x+1}-\frac{1}{1-x}=\frac{x-3}{(x+1)(x-1)}+\frac{1}{x+1}-\frac{1}{1-x}$$

Якщо ми не будемо обережні, у нас може виникнути спокуса взяти по одному з факторів і використати (x+ 1) (x− 1) (1−x) як спільний знаменник. Однак давайте спочатку зробимо два заперечення останнього з трьох дробів праворуч, заперечуючи рядок дробу і знаменник, щоб отримати

$$\frac{x-3}{x^{2}-1}+\frac{1}{x+1}-\frac{1}{1-x}=\frac{x-3}{(x+1)(x-1)}+\frac{1}{x+1}+\frac{1}{x-1}$$

Тепер ми бачимо, що достатньо спільного знаменника (x + 1) (x − 1). Давайте зробимо еквівалентні дроби з цим спільним знаменником.

$$\begin{aligned} \frac{x-3}{x^{2}-1}+\frac{1}{x+1}-\frac{1}{1-x} &=\frac{x-3}{(x+1)(x-1)}+\frac{1}{x+1} \cdot \color{blue}{\frac{x-1}{x-1}}+\frac{1}{x-1} \cdot \color{blue}{\frac{x+1}{x+1}} \\ &=\frac{x-3}{(x+1)(x-1)}+\frac{x-1}{(x+1)(x-1)}+\frac{x+1}{(x+1)(x-1)} \end{aligned}$$
Складіть чисельники і діліть на спільний знаменник. Незважаючи на те, що угруповання символів не настільки критичні в цій проблемі (через знаки плюса), ми все одно вважаємо, що це хороша практика використовувати їх.

$$\begin{aligned} \frac{x-3}{x^{2}-1}+\frac{1}{x+1}-\frac{1}{1-x} &=\frac{(x-3)+(x-1)+(x+1)}{(x+1)(x-1)} \\ &=\frac{3 x-3}{(x+1)(x-1)} \end{aligned}$$

Нарешті, завжди переконайтеся, що ваша остаточна відповідь зводиться до найнижчих термінів. Маючи на увазі цю думку, ми враховуємо чисельник в надії, що ми зможемо отримати загальний коефіцієнт для скасування.

\[\begin{aligned} \frac{x-3}{x^{2}-1}+\frac{1}{x+1}-\frac{1}{1-x} &=\frac{3(x-1)}{(x+1)(x-1)} \\ &=\frac{3(x-1)}{(x+1)(x-1)} \\ &=\frac{3}{x+1} \end{aligned}\]

Коефіцієнти x + 1 та x − 1 у знаменнику створюють обмеження x = −1 та x = 1 відповідно. Однак для всіх інших значень x ліва сторона

$$\frac{x-3}{x^{2}-1}+\frac{1}{x+1}-\frac{1}{1-x}=\frac{3}{x+1}$$

ідентична правій стороні. Знову ж таки, це легко перевіряється на графічному калькуляторі, як показано в послідовності скріншотів на малюнку$\PageIndex{4}$.

Малюнок$\PageIndex{4}$. Використання функції таблиці графічного калькулятора для перевірки результату в рівнянні (16).

Знову ж таки, зверніть увагу на повідомлення ERR (помилки) при кожному обмеженні, але також зверніть увагу, що значення Y1 і Y2 узгоджуються для всіх інших значень x.

Давайте розглянемо приклад з використанням позначення функції.

Приклад$\PageIndex{6}$

Якщо функції f і g визначені правилами $$f(x)=\frac{x}{x+2} \quad \text { and } \quad g(x)=\frac{1}{x}$$ , спростити f (x) − g (x).

Рішення

По-перше, $$f(x)-g(x)=\frac{x}{x+2}-\frac{1}{x}$$

Зверніть увагу, як спокусливо було б скасувати. Однак скасування було б помилкою в цій ситуації, оскільки віднімання вимагає спільного знаменника.

$$\begin{aligned} f(x)-g(x) &=\frac{x}{x+2} \cdot \color{blue}{\frac{x}{x}}-\frac{1}{x} \cdot \color{blue}{\frac{x+2}{x+2}} \\ &=\frac{x^{2}}{x(x+2)}-\frac{x+2}{x(x+2)} \end{aligned}$$
Віднімаємо чисельники і ділимо на спільний знаменник. Для цього потрібно, щоб ми «розподілили» знак мінус.

$$\begin{aligned} f(x)-g(x) &=\frac{x^{2}-(x+2)}{x(x+2)} \\ &=\frac{x^{2}-x-2}{x(x+2)} \end{aligned}$$

Цей результат є дійсним для всіх значень x, окрім 0 та −2. Ми залишаємо це нашим читачам, щоб переконатися, що цей результат зведений до найнижчих термінів. Можливо, ви також захочете перевірити результат на калькуляторі.

Вправа

У вправах 1 - 16 додайте або відніміть раціональні вирази, як зазначено, і спростіть свою відповідь. Вказати всі обмеження.

Вправа$\PageIndex{1}$

$\frac{7x^2−49x}{x−6}+\frac{42}{x−6}$

Відповідь

7 (x−1), надано$x \ne 6$.

Вправа$\PageIndex{2}$

$\frac{2x^2−110}{x−7}−\frac{12}{7−x}$

Вправа$\PageIndex{3}$

$\frac{27x− 9x^2}{x+3}+\frac{162}{x+3}$

Відповідь

−9 (x−6), надано$x \ne −3$.

Вправа$\PageIndex{4}$

$\frac{2x^2−28}{x+2}−\frac{10x}{x+2}$

Вправа$\PageIndex{5}$

$\frac{4x^2−8}{x−4}+\frac{56}{4−x}$

Відповідь

4 (х+4), передбачено$x \ne 4$.

Вправа$\PageIndex{6}$

$\frac{4x^2}{x−2}−\frac{36x−56}{x−2}$

Вправа$\PageIndex{7}$

$\frac{9x^2}{x−1}+\frac{72x−63}{1−x}$

Відповідь

9 (x−7), надано$x \ne 1$.

Вправа$\PageIndex{8}$

$\frac{5x^2+30}{x−6}−\frac{35x}{x−6}$

Вправа$\PageIndex{9}$

$\frac{4x^2−60x}{x−7}+\frac{224}{x−7}$

Відповідь

4 (x−8), надано$x \ne 7$.

Вправа$\PageIndex{10}$

$\frac{3x^2}{x−7}−\frac{63−30x}{7−x}$

Вправа$\PageIndex{11}$

$\frac{3x^2}{x−2}−\frac{48−30x}{2−x}$

Відповідь

3 (x−8), надано$x \ne 2$.

Вправа$\PageIndex{12}$

$\frac{4x^2−164}{x−6}−\frac{20}{6−x}$

Вправа$\PageIndex{13}$

$\frac{9x^2}{x−2}−\frac{81x−126}{x−2}$

Відповідь

9 (x−7), надано$x \ne 2$.

Вправа$\PageIndex{14}$

$\frac{9x^2}{x−8}+\frac{144x−576}{8−x}$

Вправа$\PageIndex{15}$

$\frac{3x^2−12}{x−3}+\frac{15}{3−x}$

Відповідь

3 (х+3), передбачено$x \ne 3$.

Вправа$\PageIndex{16}$

$\frac{7x^2}{x−9}−\frac{112x−441}{x−9}$

У вправах 17 - 34 додайте або відніміть раціональні вирази, як зазначено, і спростіть свою відповідь. Вказати всі обмеження.

Вправа$\PageIndex{17}$

$\frac{3x}{x^2−6x+5}+\frac{15}{x^2−14x+45}$

Відповідь

За умови$x \ne 5, 1, 9$,

$\frac{3(x+1)}{(x−1)(x−9)}$

Вправа$\PageIndex{18}$

$\frac{7x}{x^2−4x}+\frac{28}{x^2−12x+32}$

Вправа$\PageIndex{19}$

$\frac{9x}{x^2+4x−12}−\frac{54}{x^2+20x+84}$

Відповідь

За умови$x \ne −6, 2, −14$,

$\frac{9(x+2)}{(x−2)(x+14)}$

Вправа$\PageIndex{20}$

$\frac{9x}{x^2−25}−\frac{45}{x^2+20x+75}$

Вправа$\PageIndex{21}$

$\frac{5x}{x^2−21x+98}−\frac{35}{7x−x^2}$

Відповідь

За умови$x \ne 7, 14, 0$,

$\frac{5(x+14)}{x(x−14)}$

Вправа$\PageIndex{22}$

$\frac{7x}{7x−x^2}+\frac{147}{x^2+7x−98}$

Вправа$\PageIndex{23}$

$\frac{−7x}{x^2−8x+15}−\frac{35}{x^2−12x+35}$

Відповідь

За умови$x \ne 5, 3, 7$,

$\frac{−7(x+3)}{(x−3)(x−7)}$

Вправа$\PageIndex{24}$

$\frac{−6x}{x^2+2x}+\frac{12}{x^2+6x+8}$

Вправа$\PageIndex{25}$

$\frac{−9x}{x^2−12x+32}−\frac{36}{x^2−4x}$

Відповідь

За умови$x \ne 4, 8, 0$,

$\frac{−9(x+8)}{x(x−8)}$

Вправа$\PageIndex{26}$

$\frac{5x}{x^2−12x+32}−\frac{20}{4x−x^2}$

Вправа$\PageIndex{27}$

$\frac{6x}{x^2−21x+98}−\frac{42}{7x−x^2}$

Відповідь

За умови$x \ne 7, 14, 0$,

$\frac{6(x+14)}{x(x−14)}$

Вправа$\PageIndex{28}$

$\frac{−2x}{x^2−3x−10}+\frac{4}{x^2+11x+18}$

Вправа$\PageIndex{29}$

$\frac{−9x}{x^2−6x+8}−\frac{18}{x^2−2x}$

Відповідь

За умови$x \ne 2,4,0$,

$\frac{−9(x+4)}{x(x−4)}$

Вправа$\PageIndex{30}$

$\frac{6x}{5x−x^2}+\frac{90}{x^2+5x−50}$

Вправа$\PageIndex{31}$

$\frac{8x}{5x−x^2}+\frac{120}{x^2+5x−50}$

Відповідь

За умови$x \ne 5, 0, −10$,

$\frac{−8}{x+10}$

Вправа$\PageIndex{32}$

$\frac{−5x}{x^2+5x}+\frac{25}{x^2+15x+50}$

Вправа$\PageIndex{33}$

$\frac{−5x}{x^2+x−30}+\frac{30}{x^2+23x+102}$

Відповідь

За умови$x \ne −6, 5, −17$,

$\frac{−5(x+5)}{(x−5)(x+17)}$

Вправа$\PageIndex{34}$

$\frac{9x}{x^2+12x+32}−\frac{36}{x^2+4x}$

Вправа$\PageIndex{35}$

Нехай

$f(x) = \frac{8x}{x^2+6x+8}$

і

$g(x) = \frac{16}{x^2+2x}$

Обчислити f (x) −g (x) і спростити відповідь.

Відповідь

За умови$x \ne −2, −4, 0$,

$\frac{8(x−4)}{x(x+4)}$

Вправа$\PageIndex{36}$

Нехай

$f(x) = \frac{−7x}{x^2+8x+12}$

і

$g(x) = \frac{42}{x^2+16x+60}$

Обчислити f (x) +g (x) і спростити відповідь.

Вправа$\PageIndex{37}$

Нехай

$f(x) = \frac{11x}{x^2+12x+32}$

і

$g(x) = \frac{44}{−4x−x^2}$

Обчислити f (x) +g (x) і спростити відповідь.

Відповідь

За умови$x \ne −4, −8, 0$,

$\frac{11(x−8)}{x(x+8)}$

Вправа$\PageIndex{38}$

Нехай

$f(x) = \frac{8x}{x^2−6x}$

і

$g(x) = \frac{48}{x^2−18x+72}$

Обчислити f (x) +g (x) і спростити відповідь.

Вправа$\PageIndex{39}$

Нехай

$f(x) = \frac{4x}{−x−x^2}$

і

$g(x) = \frac{4}{x^2+3x+2}$

Обчислити f (x) +g (x) і спростити відповідь.

Відповідь

За умови$x \ne −1, 0, −2$,

$\frac{−4}{x+2}$

Вправа$\PageIndex{40}$

Нехай

$f(x) = \frac{5x}{x^2−x−12}$

і

$g(x) = \frac{15}{x^2+13x+30}$

Обчислити f (x) −g (x) і спростити відповідь.