7.4: Продукти та коефіцієнти раціональних функцій

У цьому розділі ми розглядаємо продукти і частки раціональних виразів. Перш ніж ми почнемо, нам потрібно встановити деякі основні визначення та техніку. Почнемо з визначення добутку двох раціональних чисел.

Визначення

Нехай a/b і c/d будуть раціональними числами. Добуток цих раціональних чисел визначається

$$\frac{a}{b} \times \frac{c}{d}=\frac{a \times c}{b \times d}, \quad \text { or more compactly, } \quad \frac{a}{b} \cdot \frac{c}{d}=\frac{a c}{b d}$$

У визначенні просто зазначено, що слід помножити чисельники кожного раціонального числа, щоб отримати чисельник твору, а також множити знаменники кожного раціонального числа, щоб отримати знаменник твору. Наприклад,

$$\frac{2}{3} \cdot \frac{5}{7}=\frac{2 \cdot 5}{3 \cdot 7}=\frac{10}{21}$$

Звичайно, ви також повинні перевірити, щоб переконатися, що ваша остаточна відповідь зведена до найнижчих термінів.

Давайте розглянемо приклад.

Приклад$\PageIndex{1}$

Спрощення добутку раціональних чисел $$\frac{6}{231} \cdot \frac{35}{10}$$

Рішення

Спочатку помножте чисельники і знаменники разом наступним чином.

$$\frac{6}{231} \cdot \frac{35}{10}=\frac{6 \cdot 35}{231 \cdot 10}=\frac{210}{2310}$$

Однак відповідь не зводиться до найнижчих термінів. Ми можемо висловити чисельник як добуток простих чисел.

$$210=21 \cdot 10=3 \cdot 7 \cdot 2 \cdot 5=2 \cdot 3 \cdot 5 \cdot 7$$

Не обов'язково розставляти фактори по зростанню, але кожен шматочок допомагає. Знаменник також може бути виражений у вигляді добутку простих чисел.

$$2310=10 \cdot 231=2 \cdot 5 \cdot 7 \cdot 33=2 \cdot 3 \cdot 5 \cdot 7 \cdot 11$$

Тепер ми можемо скасувати загальні фактори.

$$\frac{210}{2310}=\frac{2 \cdot 3 \cdot 5 \cdot 7}{2 \cdot 3 \cdot 5 \cdot 7 \cdot 11}=\frac{\not{2} \cdot \not{3} \cdot \not{5} \cdot \not{7}}{\not{2} \cdot \not{8} \cdot \not{5} \cdot \not{7} \cdot 11}=\frac{1}{11}$$

Однак такий підхід не є найефективнішим способом діяти, оскільки множення чисельників і знаменників дозволяє вирости продукції до більших чисел, як у 210/2310. Тоді трохи складніше просте множник більших чисел.

Кращий підхід полягає в тому, щоб негайно перерахувати менші чисельники та знаменники наступним чином.

$$\frac{6}{231} \cdot \frac{35}{10}=\frac{2 \cdot 3}{3 \cdot 7 \cdot 11} \cdot \frac{5 \cdot 7}{2 \cdot 5}$$

Тепер ми могли б помножити чисельники та знаменники, а потім скасувати загальні множники, які однаково збігаються з останніми обчисленнями в рівнянні (5).

Однак ми також можемо використовувати наступне правило скасування.

Правило скасування

При роботі з добутком двох і більше раціональних виразів множьте всі чисельники і знаменники, після чого скасуйте. Правило скасування просте: скасуйте коефіцієнт «зверху» за ідентичний коефіцієнт «на дні». Якщо говорити більш технічно, скасуйте будь-який коефіцієнт в будь-якому чисельнику для ідентичного множника в будь-якому знаменнику.

Таким чином, ми можемо закінчити наші обчислення, скасувавши загальні фактори, скасувавши «щось зверху для чогось внизу».

$$\frac{6}{231} \cdot \frac{35}{10}=\frac{2 \cdot 3}{3 \cdot 7 \cdot 11} \cdot \frac{5 \cdot 7}{2 \cdot 5}=\frac{\not{2} \cdot \not{8}}{\not{3} \cdot \not{7} \cdot 11} \cdot \frac{\not{5} \cdot \not{7}}{\not{2} \cdot \not{5}}=\frac{1}{11}$$

Зверніть увагу, що ми скасували 2, 3, 5 та 7 «зверху» для 2, 3, 5 та 7 «внизу».

Таким чином, ми маємо два варіанти при множенні раціональних виразів:

• Множимо чисельники і знаменники, коефіцієнт, потім скасуємо.
• Коефіцієнти чисельників і знаменників, скасувати, потім множити чисельники і знаменники.

Саме останній підхід ми будемо використовувати в цьому розділі. Давайте розглянемо інший приклад.

Приклад$\PageIndex{2}$

Спростити вираз $$\frac{x^{2}-x-6}{x^{2}+2 x-15} \cdot \frac{x^{2}-x-30}{x^{2}-2 x-8}$$ державні обмеження.

Рішення

Використовуйте ac-тест для множення кожного чисельника та знаменника. Потім скасуйте, як показано на малюнку.

\[\begin{aligned} \frac{x^{2}-x-6}{x^{2}+2 x-15} \cdot \frac{x^{2}-x-30}{x^{2}-2 x-8} &=\frac{(x+2)(x-3)}{(x-3)(x+5)} \cdot \frac{(x+5)(x-6)}{(x+2)(x-4)} \\ &=\frac{(x+2)(x-3)}{(x-3)(x+5)} \cdot \frac{(x+5)(x-4)}{(x+2)(x-4)} \\ &=\frac{x-6}{x-4} \end{aligned}\]

Знаменник першого дробу має множники x − 3 та x + 5. Отже, x = 3 або x = −5 зробить цей знаменник нулем. Тому 3 і −5 є обмеженнями.

Знаменник другого дробу має множники x + 2 та x − 4. Отже, x = −2 або x = 4 зробить цей знаменник нулем.

Тому −2 і 4 є обмеженнями. Отже, для всіх значень x, окрім обмежень −5, −2, 3 та 4, ліворуч $$\frac{x^{2}-x-6}{x^{2}+2 x-15} \cdot \frac{x^{2}-x-30}{x^{2}-2 x-8}=\frac{x-6}{x-4}$$

ідентична його правій стороні.

Для перевірки результатів можна скористатися графічним калькулятором. По-перше, завантажте ліву та праву сторони рівняння (8) у калькулятор у Y1 та Y2 у меню Y= графічного калькулятора, як показано на малюнку$\PageIndex{1}$ (a). Натисніть 2-й TBLSET і встановіть TBLStart = −6 і$\Delta \mathrm{Tb} 1=1$, як показано на малюнку$\PageIndex{1}$ (b). Переконайтеся, що AUTO виділено та вибрано клавішею ENTER як для незалежних, так і залежних змінних. Натисніть 2nd TABLE, щоб створити табличне відображення на малюнку$\PageIndex{1}$ (c).

Малюнок$\PageIndex{1}$. Використання табличних функцій графічного калькулятора для перевірки результату в рівнянні (8).

Пам'ятайте, що ліва і права частини рівняння (8) завантажені в Y1 і Y2 відповідно.

• На малюнку$\PageIndex{1}$ (c) зверніть увагу на повідомлення ERR (помилка) при обмежених значеннях x = −5 та x = −2. Однак, крім цих двох обмежень, функції Y1 і Y2 узгоджуються з усіма іншими значеннями x на малюнку$\PageIndex{1}$ (c).
• Використовуйте стрілку вниз, щоб прокрутити таблицю вниз, щоб отримати табличні результати, показані на малюнку$\PageIndex{1}$ (d). Зверніть увагу на повідомлення ERR (помилка) при обмежених значеннях x = 3 і x = 4. Однак, крім цих двох обмежень, функції Y1 і Y2 узгоджуються з усіма іншими значеннями x на малюнку$\PageIndex{1}$ (d).
• Якщо ви прокручуєте таблицю вгору або вниз, ви виявите, що функції Y1 і Y2 узгоджуються з усіма значеннями x, відмінними від обмежених значень −5, −2, 3 і 4.

Давайте розглянемо інший приклад.

Приклад$\PageIndex{3}$

Спростити $$\frac{9-x^{2}}{x^{2}+3 x} \cdot \frac{6 x-2 x^{2}}{x^{2}-6 x+9}$$ державу будь-які обмеження.

Рішення

Перший чисельник може бути врахований за допомогою різниці двох квадратів візерунка.

$$9-x^{2}=(3+x)(3-x)$$

Другий знаменник є ідеальним квадратним тріноміалом і може бути врахований як квадрат двочлена.

$$x^{2}-6 x+9=(x-3)^{2}$$

Ви захочете видалити найбільший спільний множник з першого знаменника і другого чисельника.

$$x^{2}+3 x=x(x+3) \quad \text { and } \quad 6 x-2 x^{2}=2 x(3-x)$$

Таким чином, $$\frac{9-x^{2}}{x^{2}+3 x} \cdot \frac{6 x-2 x^{2}}{x^{2}-6 x+9} \cdot=\frac{(3+x)(3-x)}{x(x+3)} \cdot \frac{2 x(3-x)}{(x-3)^{2}}$$

Нам потрібно буде виконати зміну знака або два, щоб створити загальні фактори в чисельниках і знаменниках. Отже, як у першому, так і в другому чисельнику множник a −1 від множника 3 − x для отримання 3 − x = −1 (x − 3). Оскільки порядок факторів у добутку не має значення, ми проведемо −1 на передній план у кожному конкретному випадку.

$$\frac{9-x^{2}}{x^{2}+3 x} \cdot \frac{6 x-2 x^{2}}{x^{2}-6 x+9} \cdot=\frac{-(3+x)(x-3)}{x(x+3)} \cdot \frac{-2 x(x-3)}{(x-3)^{2}}$$

Тепер ми можемо скасувати загальні фактори.

\[\begin{aligned} \frac{9-x^{2}}{x^{2}+3 x} \cdot \frac{6 x-2 x^{2}}{x^{2}-6 x+9} &=\frac{-(3+x)(x-3)}{x(x+3)} \cdot \frac{-2 x(x-3)}{(x-3)^{2}} \\ &=\frac{-(3+x)(x-3)}{x(x+3)} \cdot \frac{-2 x(x-3)}{(x-3)^{2}} \\ &=2 \end{aligned}\]

Кілька речей, які слід помітити:

• Коефіцієнти 3+ x та x + 3 однакові, тому їх можна скасувати, один зверху для одного внизу.
• Два множники x − 3 вгорі скасовуються для (x − 3) 2 (що еквівалентно (x − 3) (x − 3)) внизу.
• Х зверху скасовує х внизу.
• Ми залишились з двома знаками мінуса (два −1) та 2. Таким чином, рішення є позитивним 2.

Нарешті, перший знаменник має множники x і x + 3, тому x = 0 і x = −3 є обмеженнями (вони роблять цей знаменник рівним нулю). Другий знаменник має два множники x − 3, тому x = 3 є додатковим обмеженням.

Отже, для всіх значень x, окрім обмежених значень −3, 0 та 3, ліворуч $$\frac{9-x^{2}}{x^{2}+3 x} \cdot \frac{6 x-2 x^{2}}{x^{2}-6 x+9}=2$$

ідентична правій стороні. Знову ж таки, це твердження легко перевіряється на графічному калькуляторі, про що свідчить послідовність знімків екрану на малюнку$\PageIndex{2}$.

Малюнок$\PageIndex{2}$. Використання табличних функцій графічного калькулятора для перевірки результату в рівнянні (11).

Альтернативний підхід до задачі в рівнянні (10) полягає у відзначенні різних порядків у чисельниках та знаменниках (спадної, висхідної степенях x) і передбачити необхідність зміни знака. Тобто, зробіть зміну знака, перш ніж ви фактор.

Наприклад, заперечувати (помножити на −1) як чисельник, так і дріб першого дробу, щоб отримати

$$\frac{9-x^{2}}{x^{2}+3 x}=-\frac{x^{2}-9}{x^{2}+3 x}$$

Згідно з нашим правилом зміни знака, заперечення будь-яких двох частин дробу залишає дріб без змін.

Якщо виконати подібну зміну знака на другому дробі (нульовий чисельник і дробний бар), то ми можемо множник і скасувати загальні множники.

\[\begin{aligned} \frac{9-x^{2}}{x^{2}+3 x} \cdot \frac{6 x-2 x^{2}}{x^{2}-6 x+9} &=-\frac{x^{2}-9}{x^{2}+3 x} \cdot-\frac{2 x^{2}-6 x}{x^{2}-6 x+9} \\ &=-\frac{(x+3)(x-3)}{x(x+3)} \cdot-\frac{2 x(x-3)^{2}}{(x-3)^{2}} \\ &=-\frac{(x+3)(x-3)}{x(x+3)} \cdot-\frac{2 x(x-3)}{(x-3)^{2}} \\ &=2 \end{aligned}\]

Розподіл раціональних виразів

Просте визначення змінить задачу, яка передбачає поділ двох раціональних виразів на одне, що передбачає множення двох раціональних виразів. Тоді нічого не залишається пояснювати, бо ми вже знаємо, як помножити два раціональних вирази.

Отже, давайте мотивуємо наше визначення поділу. Припустимо, ми задаємося питанням, скільки половинок в цілому? Відповідь проста, так як дві половинки складають ціле. Таким чином, коли ми ділимо 1 на 1/2, у нас повинно вийти 2. Є дві половинки в одному цілому.

Давайте трохи піднімемо ставки і запитаємо, скільки половинок в шести? Щоб зробити проблему більш точною, уявіть, що ви замовили 6 піц, і ви розрізали кожну навпіл. Скільки у вас половинок? Знову ж таки, це легко, коли ви думаєте про проблему таким чином, відповідь 12. Таким чином,

$$6 \div \frac{1}{2}$$

(скільки половинок в шести) ідентичний

$$6 \cdot 2$$

що, звичайно, дорівнює 12. Сподіваємось, завдяки цій вступній мотивації наступне визначення не здасться занадто дивним.

Визначення

Для виконання ділення $$\frac{a}{b} \div \frac{c}{d}$$ інвертуємо другий дріб і множимо, як в $$\frac{a}{b} \cdot \frac{d}{c}$$

Таким чином, якщо ми хочемо знати, скільки половинок в 12, ми міняємо поділ на множення («інвертувати і множити»).

$$12 \div \frac{1}{2}=12 \cdot 2=24$$

Це має сенс, так як є 24 «половинки» в 12. Давайте розглянемо більш складний приклад.

Приклад$\PageIndex{4}$

Спростити $$\frac{33}{15} \div \frac{14}{10}$$

Рішення

Інвертуємо другий дріб і множимо. Після цього все, що нам потрібно зробити, це факторні чисельники і знаменники, а потім скасувати загальні множники.

$$\frac{33}{15} \div \frac{14}{10}=\frac{33}{15} \cdot \frac{10}{14}=\frac{3 \cdot 11}{3 \cdot 5} \cdot \frac{2 \cdot 5}{2 \cdot 7}=\frac{\not{8} \cdot 11}{\not{3} \cdot \not{5}} \cdot \frac{\not{2} \cdot \not{5}}{\not{2} \cdot 7}=\frac{11}{7}$$

Цікавий спосіб перевірити цей результат на вашому калькуляторі показаний в послідовності екранів на малюнку$\PageIndex{3}$.

Малюнок$\PageIndex{3}$. За допомогою калькулятора перевіряємо ділення дробів.

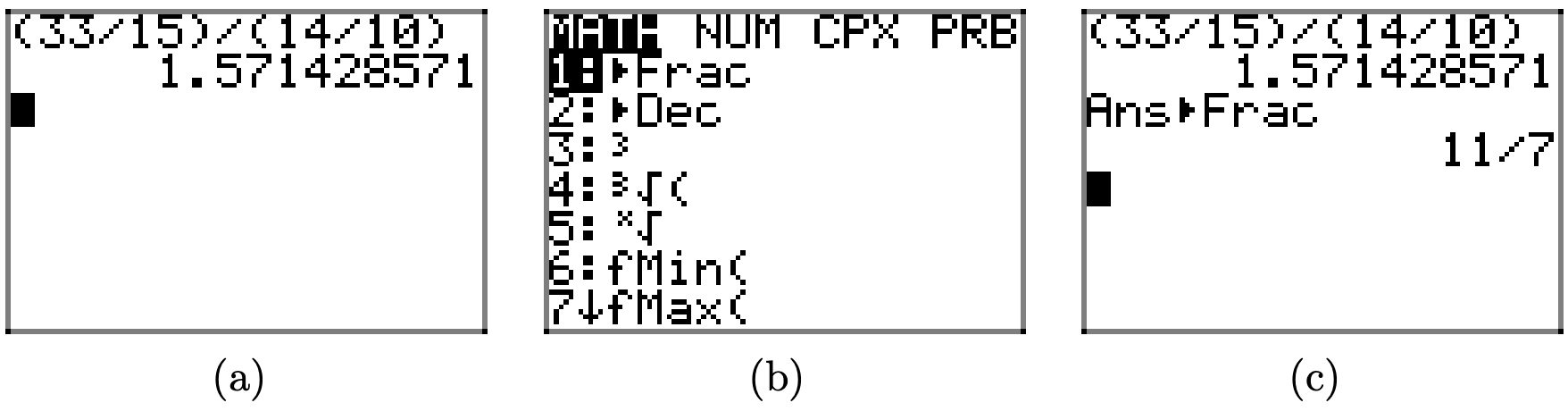
Після введення вихідної проблеми в калькулятор натисніть ENTER, потім натисніть кнопку MATH, потім виберіть 1: I Frac з меню і натисніть ENTER. Результат показаний на малюнку$\PageIndex{3}$ (в), який узгоджується з нашим розрахунком вище.

Давайте розглянемо інший приклад.

Приклад$\PageIndex{5}$

Спростити $$\frac{9+3 x-2 x^{2}}{x^{2}-16} \div \frac{4 x^{3}-9 x}{2 x^{2}+5 x-12}$$ державні обмеження.

Рішення

Зверніть увагу, що порядок першого чисельника відрізняється від інших чисельників і знаменників, тому ми «передбачаємо» необхідність зміни знака, заперечуючи чисельник і дріб першого дробу. Також інвертуємо другий дріб і міняємо ділення на множення («інвертувати і множити»).

$$-\frac{2 x^{2}-3 x-9}{x^{2}-16} \cdot \frac{2 x^{2}+5 x-12}{4 x^{3}-9 x}$$

Чисельник у першому дробі рівняння (17) є квадратичним триноміалом, з ac = (2) (−9) = −18. Пара цілих чисел 3 і −6 має добуток −18 і суму −3. Отже,

$$\begin{aligned} 2 x^{2}-3 x-9 &=2 x^{2}+3 x-6 x-9 \\ &=x(2 x+3)-3(2 x+3) \\ &=(x-3)(2 x+3) \end{aligned}$$

Знаменник першого дробу в рівнянні (17) легко множник за допомогою різниці двох квадратів шаблону.

$$x^{2}-16=(x+4)(x-4)$$

Чисельник другого дробу у рівнянні (17) є квадратичним триноміалом, з ac = (2) (−12) = −24. Пари цілих чисел −3 та 8 мають добуток −24 та суму 5. Отже,

$$\begin{aligned} 2 x^{2}+5 x-12 &=2 x^{2}-3 x+8 x-12 \\ &=x(2 x-3)+4(2 x-3) \\ &=(x+4)(2 x-3) \end{aligned}$$

Щоб множити знаменник останнього дробу в рівнянні (17), спочатку витягніть найбільший спільний коефіцієнт (в даному випадку x), потім завершіть факторизацію, використовуючи різницю двох квадратів шаблону.

$$4 x^{3}-9 x=x\left(4 x^{2}-9\right)=x(2 x+3)(2 x-3)$$

Тепер ми можемо замінити кожен чисельник і знаменник у рівнянні (17) на його факторизацію, а потім скасувати загальні множники.

\[\begin{aligned}-\frac{2 x^{2}-3 x-9}{x^{2}-16} \cdot \frac{2 x^{2}+5 x-12}{4 x^{3}-9 x} &=-\frac{(x-3)(2 x+3)}{(x+4)(x-4)} \cdot \frac{(x+4)(2 x-3)}{x(2 x+3)(2 x-3)} \\ &=-\frac{(x-3)(2 x+3)}{(x+4)(x-4)} \cdot \frac{(x+4)(2 x-3)}{x(2 x+3)(2 x-3)} \\ &=-\frac{x-3}{x(x-4)} \end{aligned}\]

Останній знаменник має множники x та x − 4, тому x = 0 та x = 4 є обмеженнями. У тілі нашої роботи знаменник першого дробу має множники x + 4 та x − 4. Ми вже бачили множник x − 4, тому лише коефіцієнт x + 4 додає нове обмеження, x = −4. Знову ж таки, у тілі нашої роботи знаменник другого дробу має множники x, 2x + 3 та 2x − 3, тому ми додали обмеження x = 0, x = −3/2 та x = 3/2.

Тут є одна хитрість, яку можна легко не помітити. У тілі нашої роботи чисельник другого дробу спочатку був знаменником, перш ніж ми перевернули дріб. Отже, ми повинні розглянути, що робить цей чисельник нульовим, а також. На щастя, множниками в цьому чисельнику є x + 4 та 2x − 3, і ми вже розглядали обмеження, що створюються цими факторами.

Отже, для всіх значень x, окрім обмежених значень −4, −3/2, 0, 3/2 та 4, ліворуч

$$\frac{9+3 x-2 x^{2}}{x^{2}-16} \div \frac{4 x^{3}-9 x}{2 x^{2}+5 x-12}=-\frac{x-3}{x(x-4)}$$

ідентична правій стороні.

Знову ж таки, це твердження легко перевіряється за допомогою графічного калькулятора, про що частково підтверджується (вам доведеться прокрутити вниз, щоб побачити останнє обмеження) у послідовності знімків екрана на малюнку$\PageIndex{4}$.

Малюнок$\PageIndex{4}$. Використовуючи табличну функцію калькулятора для перевірки результату в рівнянні (18).

Альтернативні позначення. Зверніть увагу, що дробовий вираз a/b означає «a ділиться на b», тому ми можемо використовувати це еквівалентне позначення для$a \div b$. Наприклад, вираз

$$\frac{9+3 x-2 x^{2}}{x^{2}-16} \div \frac{4 x^{3}-9 x}{2 x^{2}+5 x-12}$$

еквівалентний виразу

$$\frac{\frac{9+3 x-2 x^{2}}{x^{2}-16}}{\frac{4 x^{3}-9 x}{2 x^{2}+5 x-12}}$$

Давайте розглянемо приклад цього позначення у використанні.

Приклад$\PageIndex{6}$

Враховуючи це $$f(x)=\frac{x}{x+3} \quad \text { and } \quad g(x)=\frac{x^{2}}{x+3}$$ , спростити як f (x) g (x), так і f (x) /g (x).

Рішення

По-перше, множення. Можливої скасування немає, тому просто множимо чисельники і знаменники.

$$f(x) g(x)=\frac{x}{x+3} \cdot \frac{x^{2}}{x+3}=\frac{x^{3}}{(x+3)^{2}}$$

Цей результат є дійсним для всіх значень x, окрім −3.

З іншого боку, $$\frac{f(x)}{g(x)}=\frac{\frac{x}{x+3}}{\frac{x^{2}}{x+3}}=\frac{x}{x+3} \div \frac{x^{2}}{x+3}$$

Коли ми «інвертуємо і множимо», то скасовуємо, отримуємо $$\frac{f(x)}{g(x)}=\frac{x}{x+3} \cdot \frac{x+3}{x^{2}}=\frac{1}{x}$$ . Цей результат є дійсним для всіх значень x, окрім −3 та 0.

Вправа

У вправах 1 - 10 зменшуйте продукт до однієї фракції в найнижчих показниках.

Вправа$\PageIndex{1}$

$\frac{108}{14} \cdot \frac{6}{100}$

Відповідь

$\frac{81}{175}$

Вправа$\PageIndex{2}$

$\frac{75}{63} \cdot \frac{18}{45}$

Вправа$\PageIndex{3}$

$\frac{189}{56} \cdot \frac{12}{27}$

Відповідь

$\frac{3}{2}$

Вправа$\PageIndex{4}$

$\frac{45}{72} \cdot \frac{63}{64}$

Вправа$\PageIndex{5}$

$\frac{15}{36} \cdot \frac{28}{100}$

Відповідь

$\frac{7}{60}$

Вправа$\PageIndex{6}$

$\frac{189}{49} \cdot \frac{32}{25}$

ВПРАВА$\PageIndex{7}$

$\frac{21}{100} \cdot \frac{125}{16}$

Відповідь

$\frac{105}{64}$

Вправа$\PageIndex{8}$

$\frac{21}{35} \cdot \frac{49}{45}$

Вправа$\PageIndex{9}$

$\frac{56}{20} \cdot \frac{98}{32}$

Відповідь

$\frac{343}{40}$

Вправа$\PageIndex{10}$

$\frac{27}{125} \cdot \frac{4}{12}$

У вправах 11 - 34 множити і спростити. Вказати всі обмеження.

Вправа$\PageIndex{11}$

$\frac{x+6}{x^2+16x+63} \cdot \frac{x^2+7x}{x+4}$

Відповідь

За умови$x \ne −9, −7, −4$,

$\frac{x(x+6)}{(x+9)(x+4)}$

Вправа$\PageIndex{12}$

$\frac{x^2+9x}{x^2−25} \cdot \frac{x^2−x−20}{−18−11x−x^2}$

Вправа$\PageIndex{13}$

$\frac{x^2+7x+10}{x^2−1} \cdot \frac{−9+10x−x^2}{x^2+9x+20}$

Відповідь

За умови$x \ne 1, −1, −4, −5$,

$−\frac{(x+2)(x−9)}{(x+1)(x+4)}$

Вправа$\PageIndex{14}$

$\frac{x^2+5x}{x−4}\ cdot \frac{x−2}{x^2+6x+5}$

Вправа$\PageIndex{15}$

$\frac{x^2−5x}{x^2+2x−48} \cdot \frac{x^2+11x+24}{x^2−x}$

Відповідь

За умови$x \ne −8, 6, 1, 0$,

$\frac{(x−5)(x+3)}{(x−6)(x−1)}$

Вправа$\PageIndex{16}$

$\frac{x^2−6x−27}{x^2 +10x+24} \cdot \frac{x^2 +13x+42}{x^2−11x+18}$

Вправа$\PageIndex{17}$

$\frac{−x−x^2}{x^2−9x+8} \cdot \frac{x^2−4x+3}{x^2+4x+3}$

Відповідь

За умови$x \ne 1, 8, −3, −1$,

$−\frac{x(x−3)}{(x−8)(x+3)}$

Вправа$\PageIndex{18}$

$\frac{x^2−12x+35}{x^2+2x−15} \cdot \frac{45+4x−x^2}{x^2+x−30}$

Вправа$\PageIndex{19}$

$\frac{x+2}{7−x} \cdot \frac{x^2+x−56}{x^2+7x+6}$

Відповідь

За умови$x \ne 7, −1, −6$,

$−\frac{(x+2)(x+8)}{(x+1)(x+6)}$

Вправа$\PageIndex{20}$

$\frac{x^2−2x−15}{x^2 +x} \cdot \frac{x^2+7x}{x^2+12x+27}$

Вправа$\PageIndex{21}$

$\frac{x^2−9}{x^2−4x−45} \cdot \frac{x−6}{−3−x}$

Відповідь

За умови$x \ne −3, −5, 9$,

$−\frac{(x−3)(x−6)}{(x−5)(x−3)}$

Вправа$\PageIndex{22}$

$\frac{x^2−12x+27}{x−5} \cdot \frac{x−4}{x^2−18x+8}$

Вправа$\PageIndex{23}$

$\frac{x+5}{x^2−2x−24} \cdot \frac{x^2+12x+32}{x+7}$

Відповідь

За умови$x \ne −8, −4, −7$,

$\frac{(x+5)(x−6)}{(x+8)(x+7)}$

Вправа$\PageIndex{24}$

$\frac{x^2−36}{x^2+11x+24} \cdot \frac{−8−x}{x+4}$

Вправа$\PageIndex{25}$

$\frac{x−5}{x^2−8x+12} \cdot \frac{x^2−12x+36}{x−8}$

Відповідь

За умови$x \ne 2, 6, 8$,

$\frac{(x−5)(x−6)}{(x−2)(x−8)}$

Вправа$\PageIndex{26}$

$\frac{x^2−5x−36}{x−1} \cdot \frac{x−5}{x^2−81}$

Вправа$\PageIndex{27}$

$\frac{x^2 +2x−15}{x^2−10x+16} \cdot \frac{x^2−7x+10}{3x^2+13x−10}$

Відповідь

За умови$x \ne 2, 8, \frac{2}{3}, −5$,

$\frac{(x−3)(x−5)}{(3x−2)(x−8)}$

Вправа$\PageIndex{28}$

$\frac{5x^2+14x−3}{x+9} \cdot \frac{x−7}{x^2+10x+21}$

Вправа$\PageIndex{29}$

$\frac{x^2−4}{x^2+2x−63} \cdot \frac{x^2+6x−27}{x^2−6x−16}$

Відповідь

За умови$x \ne −9, 7, 8, −2$,

$\frac{(x−2)(x−3)}{(x−7)(x−8)}$

Вправа$\PageIndex{30}$

$\frac{x^2+5x+6}{x^2−3x} \cdot \frac{x^2−5x}{x^2+9x+18}$

Вправа$\PageIndex{31}$

$\frac{x−1}{x^2+2x−63} \cdot \frac{x^2−81}{x+4}$

Відповідь

За умови$x \ne 7, −9, −4$,

$\frac{(x−1)(x−9)}{(x−7)(x+4)}$

Вправа$\PageIndex{32}$

$\frac{x^2+9x}{x^2+7x+12} \cdot \frac{27+6x−x^2}{x^2−5x}$

Вправа$\PageIndex{33}$

$\frac{5−x}{x+3} \cdot \frac{x^2+3x−18}{2x^2−7x−15}$

Відповідь

Надано$x \ne −3, −\frac{3}{2}, 5$

$−\frac{(x+6)(x−3)}{(2x+3)(x+3)}$

Вправа$\PageIndex{34}$

$\frac{4x^2+21x+5}{18−7x−x^2} \cdot \frac{x^2+11x+18}{x^2−25}$

У вправах 35 - 58 розділіть і спрощуйте. Вказати всі обмеження.

Вправа$\PageIndex{35}$

$\frac{\frac{x^2−14x+48}{x^2+10x+16}}{\frac{−24+11x−x^2}{x^2−x−72}}$

Відповідь

За умови$x \ne −8, −2, 9, 3, 8$,

$−\frac{(x−6)(x−9)}{(x+2)(x−3)}$

Вправа$\PageIndex{36}$

$\frac{x−1}{x^2−14x+48​} \div \frac{x+5}{x^2−3x−18}$

Вправа$\PageIndex{37}$

$\frac{x^2−1}{x^2−7x+12​} \div \frac{x^2+6x+5}{−24+10x−x^2}$

Відповідь

За умови$x \ne 4, 3, 6, −5, −1$,

$−\frac{(x−1)(x−6)}{(x−3)(x+5)}$

Вправа$\PageIndex{38}$

$\frac{x^2−13x+42}{x^2−2x−63} \div \frac{x^2−x−42}{x^2+8x+7}$

Вправа$\PageIndex{39}$

$\frac{x^2−25}{x+1} \div \frac{5x^2+23x−10}{x−3}$

Відповідь

За умови$x \ne −1, \frac{2}{5}, −5, 3$,

$\frac{(x−5)(x−3)​​​​​​}{(5x−2)(x+1)}$

Вправа$\PageIndex{40}$

$\frac{\frac{x^2−3x}{x^2−7x+6}}{\frac{x^2−4x}{3x^2−11x−42}}$

Вправа$\PageIndex{41}$

$\frac{\frac{x^2+10x+21}{x−4}}{\frac{x^2+3x}{x+8}}$

Відповідь

За умови$x \ne 4, 0, −3, −8$,

$\frac{(x+7)(x+8)}{x(x−4)}$

Вправа$\PageIndex{42}$

$\frac{x^2+8x+15}{x^2−14x+45} \div \frac{x^2+11x+30}{−30+11x−x^2}$

Вправа$\PageIndex{43}$

$\frac{\frac{x^2−6x−16}{x^2+x−42}}{\frac{x^2−64}{x^2+12x+35}}$

Відповідь

За умови$x \ne −7, 6, −5, −8, 8$,

$\frac{(x+2)(x+5)}{(x−6)(x+8)}$

Вправа$\PageIndex{44}$

$\frac{\frac{x^2+3x+2}{x^2−9x+18}}{\frac{x^2+7x+6}{x^2−6x}}$

Вправа$\PageIndex{45}$

$\frac{\frac{x^2+12x+35}{x+4}}{\frac{x^2+10x+25}{x+9}}$

Відповідь

За умови$x \ne −4, −5, −9$,

$\frac{(x+7)(x+9)}{(x+4)(x+5)}$

Вправа$\PageIndex{46}$

$\frac{x^2−8x+7}{x^2+3x−18} \div \frac{x^2−7x}{x^2+6x−27}$

Вправа$\PageIndex{47}$

$\frac{x^2+x−30}{x^2+5x−36} \div \frac{−6−x}{x+8}$

Відповідь

За умови$x \ne 4, −9, −8, −6$,

$−\frac{(x−5)(x+8)}{(x−4)(x+9)}$

Вправа$\PageIndex{48}$

$\frac{\frac{2x−x^2}{x^2−15x+54}}{\frac{x^2+x}{x^2−11x+30}}$

Вправа$\PageIndex{49}$

$\frac{\frac{x^2−9x+8}{x^2−9}}{\frac{x^2−8x−15}{−8x−x^2}}$

Відповідь

За умови$x \ne −3, 3, −5, 0, 8$,

$−\frac{(x−1)(x+5)}{x(x−3)}$

Вправа$\PageIndex{50}$

$\frac{x+5}{x^2+2x+1} \div \frac{x−2}{x^2+10x+9}$

Вправа$\PageIndex{51}$

$\frac{\frac{x^2−4}{x+8}}{\frac{x^2−10x+16}{x+3}}$

Відповідь

За умови$x \ne −8, 8, 2, −3$,

$\frac{(x+2)(x+3)}{(x+8)(x−8)}$

Вправа$\PageIndex{52}$

$\frac{27−6x−x^2}{x^2+9x+20} \div \frac{x^2−12x+27}{x^2+5x}$

Вправа$\PageIndex{53}$

$\frac{\frac{x^2+5x+6}{x^2 − 36}}{\frac{x−7}{−6−x}}$

Відповідь

За умови$x \ne 6, −6, 7$,

$−\frac{(x+2)(x+3)}{(x−6)(x−7)}$

Вправа$\PageIndex{54}$

$\frac{2−x}{x−5} \div \frac{x^2+3x−10}{x^2−14x+48}$

Вправа$\PageIndex{55}$

$\frac{\frac{x+3}{x^2 +4x−12}}{\frac{x−4}{x^2−36}}$

Відповідь

За умови$x \ne 2, −6, 4, 6$,

$\frac{(x+3)(x−6)}{(x−2)(x−4)}$

Вправа$\PageIndex{56}$

$\frac{x+3}{x^2−x−2​​​​​​} \div \frac{x}{x^2−3x−4}$

Вправа$\PageIndex{57}$

$\frac{x^2−11x+28}{x^2+5x+6} \div \frac{7x^2−30x+8}{x^2−x−6}$

Відповідь

За умови$x \ne −2, −3, 3, \frac{2}{7}, 4$,

$\frac{(x−7)(x−3)}{(7x−2)(x+3)}$

Вправа$\PageIndex{58}$

$\frac{\frac{x−7}{3−x}}{\frac{2x^2+3x−5}{x^2−12x+27}}$

Вправа$\PageIndex{59}$

Нехай

$f(x) = \frac{x^2−7x+10}{x^2+4x−21}$

і

$g(x) = \frac{5x−x^2}{x^2+15x+56}$

Обчислити$\frac{f(x)}{g(x)}$ і спростити відповідь.

Відповідь

За умови$x \ne −7, 3, −8, 0, 5$,

$−\frac{(x−2)(x+8)}{x(x−3)}$

Вправа$\PageIndex{60}$

Нехай

$f(x) = \frac{x^2+15x+56}{x^2−x−20}$

і

$g(x) = \frac{−7−x}{x+1}$

Обчислити$\frac{f(x)}{g(x)}$ і спростити відповідь.

Вправа$\PageIndex{61}$

Нехай

$f(x) = \frac{x^2+12x+35}{x^2+4x−32}$

і

$g(x) = \frac{x^2−2x−35}{x^2+8x}$

Обчислити$\frac{f(x)}{g(x)}$ і спростити відповідь.

Відповідь

За умови$x \ne −8, 4, 0, 7, −5$,

$\frac{x(x+7)}{(x−4)(x−7)}$

Вправа$\PageIndex{62}$

Нехай

$f(x) = \frac{x^2+4x+3}{x−1}$

і

$g(x) = \frac{x^2−4x−21}{x+5}$

Обчислити$\frac{f(x)}{g(x)}$ і спростити відповідь.

Вправа$\PageIndex{63}$

Нехай

$f(x) = \frac{x^2+x−20}{x}$

і

$g(x) = \frac{x−1}{x^2−2x−35}$

Обчислити f (x) g (x) і спростити відповідь.

Відповідь

За умови$x \ne 0, 7, −5$,

$\frac{(x−4)(x−1)}{x(x−7)}$

Вправа$\PageIndex{64}$

Нехай

$f(x) = \frac{x^2+10x+24}{x^2−13x+42}$

і

$g(x) = \frac{x^2−6x−7}{x^2+8x+12}$

Обчислити f (x) g (x) і спростити відповідь.

Вправа$\PageIndex{65}$

Нехай
$f(x) = \frac{x+5}{−6−x}$

і

$g(x) = \frac{x^2+8x+12}{x^2−49}$

Обчислити f (x) g (x) і спростити відповідь.

Відповідь

За умови$x \ne −6, −7, 7$,

$−\frac{(x+5)(x+2)}{(x+7)(x−7)}$

Вправа$\PageIndex{66}$

Нехай

$f(x)= \frac{8−7x−x^2}{x^2−8x−9}$

і

$g(x) = \frac{x^2−6x−7}{x^2−6x+5}$

Обчислити f (x) g (x) і спростити відповідь.