4.5: Додавання та віднімання дробів

Last updated
Save as PDF

Page ID: 57367

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Пол і Тоні замовляють піцу, яка була розрізана на вісім рівних скибочок. Таким чином, кожен шматочок становить 1/8 всієї піци. Пол їсть дві скибочки (затінені світло-сірим кольором на малюнку$\PageIndex{1}$), або 2/8 всієї піци. Тоні з'їдає три скибочки (затінені світло-червоним кольором (або більш темним відтінком сірого в чорно-білому друку$\PageIndex{1}$) на малюнку), або 3/8 всієї піци.

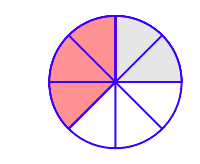
Знімок екрана 2019-08-30 о 4.09.40 PM.png — Малюнок$\PageIndex{1}$: Пол їсть два скибочки (2/8), а Тоні їсть три скибочки (3/8).

Повинно бути зрозуміло, що разом Пол і Тоні з'їдають п'ять скибочок, або 5/8 всієї піци. Це відображає той факт, що

\[ \frac{2}{8} + \frac{3}{8} = \frac{5}{8}.\nonumber \]

Це демонструє, як додати два дроби із загальним (однаковим) знаменником. Зберігайте спільний знаменник і додайте чисельники. Тобто,

\[ \begin{align*} \frac{2}{8} + \frac{3}{8} &= \frac{2 + 3}{8} ~ && \textcolor{red}{ \text{ Keep denominator; add numerators.}} \\ &= \frac{5}{8} ~ && \textcolor{red}{ \text{ Simplify numerator.}} \end{align*} \]

Додавання дробів із загальними знаменниками

Нехай a/c і b/c - два дроби із загальним (однаковим) знаменником. Їх сума визначається як

\[ \frac{a}{c} + \frac{b}{c} = \frac{a + b}{c}\nonumber \]

Тобто скласти два дроби, що мають спільні знаменники, зберегти загальний знаменник і скласти їх чисельники.

Аналогічне правило дотримується і для віднімання.

Віднімання дробів із загальними знаменниками

Нехай a/c і b/c - два дроби із загальним (однаковим) знаменником. Їх відмінність визначається як

\[ \frac{a}{c} - \frac{b}{c} = \frac{a-b}{c}.\nonumber \]

Тобто відняти два дроби, що мають спільні знаменники, зберегти загальний знаменник і відняти їх чисельники.

Приклад$\PageIndex{1}$

Знайти суму 4/9 і 3/9.

Рішення

Зберігайте спільний знаменник і додайте чисельники.

\[ \begin{aligned} \frac{4}{9} + \frac{3}{9} &= \frac{4+3}{9} ~ & \textcolor{red}{ \text{ Keep denominator; add numerators.}} \\ &= \frac{7}{9} ~ & \textcolor{red}{ \text{ Simplify numerator.}} \end{aligned}\nonumber \]

Вправа$\PageIndex{1}$

Додати:

\[ \frac{1}{8} + \frac{2}{8}\nonumber \]

Відповідь: 3/8

Приклад$\PageIndex{2}$

Відніміть 5/16 з 13/16.

Рішення

Зберігайте спільний знаменник і відніміть чисельники.

\[ \begin{aligned} \frac{13}{16} - \frac{5}{16} &= \frac{13-5}{16} ~ & \textcolor{red}{ \text{ Keep denominator; subtract numerators.}} \\ &=\frac{8}{16} ~ & \textcolor{red}{ \text{ Simplify numerator.}} \end{aligned}\nonumber \]

Звичайно, як ми дізналися в розділі 4.1, ми завжди повинні зводити остаточну відповідь до найнижчих показників. Один із способів досягти цього в цьому випадку - розділити чисельник і знаменник на 8, найбільший спільний дільник 8 і 16.

\[ \begin{aligned} = \frac{8 \div 8}{16 \div 8} ~ & \textcolor{red}{ \text{ Divide numerator and denominator by 8.}} \\ = \frac{1}{2} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]

Вправа$\PageIndex{2}$

Відніміть:

\[ \frac{11}{12} - \frac{7}{12}\nonumber \]

Відповідь: 1/3

Приклад$\PageIndex{3}$

Спростити:

\[ \frac{3}{x} - \left( - \frac{7}{x} \right) .\nonumber \]

Рішення

Обидва дроби мають спільний знаменник.

\[ \begin{aligned} \frac{3}{x} - \left( - \frac{7}{x} \right) &= \frac{3}{x} + \frac{7}{x} ~ & \textcolor{red}{ \text{ Add the opposite.}} \\ &= \frac{3+7}{x} ~ & \textcolor{red}{ \text{ Keep denominator, add numerators.}} \\ &= \frac{10}{x} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

Додавання дробів з різними знаменниками

Розглянемо суму

\[ \frac{4}{9} + \frac{1}{6}.\nonumber \]

Ми не можемо додати ці дроби, оскільки вони не мають спільного знаменника. Отже, що робити?

Цілі

Для того щоб скласти два дроби з різними знаменниками, нам потрібно:

Знайти спільний знаменник для заданих дробів.
Складіть дроби із загальним знаменником, які еквівалентні вихідним дроби.

Якщо ми виконаємо два пункти в «Цілі», ми зможемо знайти суму заданих дробів.

Отже, з чого почати? Нам потрібно знайти спільний знаменник, але не просто будь-який спільний знаменник. Погодьмося, що ми хочемо зберегти цифри якомога менше і знайти найменш спільний знаменник.

Визначення: Найменш спільний знаменник

Найменшим спільним знаменником (РК) для набору дробів є найменше число, що ділиться на кожен із знаменників заданих дробів.

Розглянемо ще раз суму, яку ми хочемо знайти:

\[ \frac{4}{9} + \frac{1}{6} .\nonumber \]

Знаменники - 9 і 6. Ми хочемо знайти найменш спільний знаменник, найменше число, яке ділиться як на 9, так і на 6. Ряд кандидатів спадає на думку: 36, 54 та 72 всі діляться на 9 і 6, щоб назвати декілька. Але найменше число, яке ділиться і на 9, і на 6, - це 18. Це найменш спільний знаменник для 9 і 6.

Тепер переходимо до другого пункту в «Голі». Нам потрібно зробити дроби, що мають 18 як знаменник, еквівалентні 4/9 і 1/6. У випадку з 4/9, якщо помножити і чисельник і знаменник на 2, то отримаємо

\[ \begin{aligned} \frac{4}{9} &= \frac{4 \cdot 2}{9 \cdot 2} ~ & \textcolor{red}{ \text{ Multiply numerator and denominator by 2.}} \\ &= \frac{8}{18}. ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]

У випадку 1/6, якщо помножити і чисельник і знаменник на 3, то отримаємо

\[ \begin{aligned} \frac{1}{6} &= \frac{1 \cdot 3}{6 \cdot 3} ~ & \textcolor{red}{ \text{ Multiply numerator and denominator by 3.}} \\ &= \frac{3}{18}. ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]

Як правило, ми організуємо нашу роботу наступним чином.

\[ \begin{aligned} \frac{4} + \frac{1}{6} &= \frac{4 \cdot \textcolor{red}{2}}{9 \cdot \textcolor{red}{2}} + \frac{1 \cdot \textcolor{red}{3}}{6 \cdot \textcolor{red}{3}} ~ & \textcolor{red}{ \text{ Equivalent fractions with LCD = 18.}} \\ &= \frac{8}{18} + \frac{3}{18} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \\ &= \frac{8+3}{18} ~ & \textcolor{red}{ \text{ Keep common denominator; add numerators.}} \\ &= \frac{11}{18} ~ & \textcolor{red}{ \text{ Simplify numerator.}} \end{aligned}\nonumber \]

Підіб'ємо підсумки процедури.

Додавання або віднімання дробів з різними знаменниками

Знайдіть РК-дисплей, найменше число ділиться на всі знаменники заданих дробів.
Створюйте дроби, використовуючи РК-дисплей як знаменник, еквівалентний вихідним дроби.
Додайте або відніміть отримані еквівалентні дроби. Спростити, в тому числі звести остаточну відповідь до найнижчих термінів.

Приклад$\PageIndex{4}$

Спростити:$ \displaystyle \frac{3}{5} - \frac{2}{3}$.

Рішення

Найменше число, ділене як на 5, так і на 3, дорівнює 15.

\[ \begin{aligned} \frac{3}{5} - \frac{2}{3} &= \frac{3 \cdot \textcolor{red}{3}}{5 \cdot \textcolor{red}{3}} - \frac{2 \cdot \textcolor{red}{5}}{3 \cdot \textcolor{red}{5}} ~ & \textcolor{red}{ \text{ Equivalent fractions with LCD = 15.}} \\ &= \frac{9}{15} - \frac{10}{15} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \\ &= \frac{9-10}{15} ~ & \textcolor{red}{ \text{ Keep LCD; subtract numerators.}} \\ &= \frac{-1}{15} ~ & \textcolor{red}{ \text{ Simplify numerator.}} \end{aligned}\nonumber \]

Хоча ця відповідь цілком прийнятна, негативний розділений на позитивний дає нам негативну відповідь, тому ми також могли б написати

\[ = - \frac{1}{15}.\nonumber \]

Вправа$\PageIndex{4}$

Відніміть:

\[ \frac{3}{4} - \frac{7}{5}\nonumber \]

Відповідь: -13/20

Приклад$\PageIndex{5}$

Спростити:$-\frac{1}{4} - \frac{5}{6}$.

Рішення

Найменше число, ділене як на 4, так і на 6, дорівнює 12.

\[ \begin{aligned} -\frac{1}{4} - \frac{5}{6} &= - \frac{1 \cdot \textcolor{red}{3}}{4 \cdot \textcolor{red}{3}} - \frac{5 \cdot \textcolor{red}{2}}{6 \cdot \textcolor{red}{2}} ~ & \textcolor{red}{ \text{ Equivalent fractions with LCD =12.}} \\ &= - \frac{3}{12} - \frac{10}{12} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \\ &= \frac{-3-10}{12} ~ & \textcolor{red}{ \text{ Keep LCD; subtract numerators.}} \\ &= \frac{-13}{12} ~ & \textcolor{red}{ \text{ Simplify numerator.}} \end{aligned}\nonumber \]

Вправа$\PageIndex{5}$

Відніміть:$-\frac{3}{8} - \frac{1}{12}$

Відповідь: -11/24

Приклад$\PageIndex{6}$

Спростити:$\frac{5}{x} + \frac{3}{4}$.

Рішення

Найменше число, що ділиться як на 4, так і на x, дорівнює 4x.

\[ \begin{aligned} \frac{5}{x} + \frac{3}{4} = \frac{5 \cdot \textcolor{red}{4}}{x \cdot \textcolor{red}{4}} + \frac{3 \cdot \textcolor{red}{x}}{4 \cdot \textcolor{red}{x}} ~ & \textcolor{red}{ \text{ Equivalent fractions with LCD = }4x.} \\ = = \frac{20}{4x} + \frac{3x}{4x} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \\ = \frac{20 + 3x}{4x} ~ & \textcolor{red}{ \text{ Keep LCD; add numerators.}} \end{aligned}\nonumber \]

Вправа$\PageIndex{6}$

Додати:

\[ \frac{5}{z} + \frac{2}{3}\nonumber \]

Відповідь: \[ \frac{15+2z}{3z}\nonumber \]

Приклад$\PageIndex{7}$

Спростити:$\frac{2}{3}- \frac{x}{5}$.

Рішення

Найменше число, ділене як на 3, так і на 5, дорівнює 15.

\[ \begin{aligned} \frac{2}{3} - \frac{x}{5} = \frac{2 \cdot \textcolor{red}{5}}{3 \cdot \textcolor{red}{5}} - \frac{x \cdot \textcolor{red}{3}}{5 \cdot \textcolor{red}{3}} ~ & \textcolor{red}{ \text{ Equivalent fractions with LCD = 15.}} \\ = \frac{10}{15} - \frac{3x}{15} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \\ = \frac{10 - 3x}{15} ~ & \textcolor{red}{ \text{ Keep LCD; subtract numerators.}} \end{aligned}\nonumber \]

Найменш поширене кратне

Спочатку визначаємо кратне числу.

Визначення: Кратні

Кратні числу d - це 1 d, 2 d, 3 d, 4 d і т.д. тобто кратні d - числа nd, де n - натуральне число.

Наприклад, кратні 8 - це 1 · 8, 2 · 8, 3 · 8, 4 · 8 і т.д., або еквівалентно 8, 16, 24, 32 і т.д.

Визначення: Найменш поширене кратне

Найменш поширеним кратним (НКМ) множини чисел є найменшим числом, кратним кожному числу заданої множини. Порядок знаходження НКМ наступний:

Перерахуйте всі кратні кожному числу в заданому наборі чисел.
Перерахуйте множники, які є спільними.
Виберіть найменший з кратних, які є спільними.

Приклад$\PageIndex{7}$

Знайдіть найменш поширене кратне (НКМ) 12 і 16.

Рішення

Перерахуйте кратні 12 і 16.

Кратні 12:12, 24, 36, 48, 60, 72, 84, 96,...

Кратні 16:16, 32, 48, 64, 80, 96, 112,...

Виберіть загальні кратні.

Загальні кратні: 48, 96,...

LCM є найменшим із загальних кратних.

СМ (12,16) = 48

Вправа$\PageIndex{7}$

Знайдіть найменш спільний знаменник 6 і 9.

Відповідь: 18

Важливе спостереження

Найменш спільний знаменник - найменш спільний кратний знаменникам.

Наприклад, припустимо, ваша проблема 5/12 + 5/16. РК-дисплей - це найменше число, що ділиться як на 12, так і на 16. Це число 48, що також є LCM 12 і 16. Тому процедура пошуку НКМ може бути використана і для пошуку РК-дисплея.

Найменш поширене множинне використання первинної факторизації

Ви також можете знайти LCM за допомогою простої факторизації.

LCM За основною факторизації

Щоб знайти НКМ за набором цифр, виконайте таку процедуру:

Запишіть просту факторизацію для кожного числа в компактному вигляді, використовуючи показники.
LCM знаходять, записуючи кожен фактор, який з'являється на кроці 1, до найвищої потужності цього фактора, який з'являється.

Приклад$\PageIndex{8}$

Використовуйте просте факторизацію, щоб знайти найменш спільний кратний знайти найменш спільний знаменник 18 і 24. (LCM) 12 і 16.

Рішення

Просте число 12 і 16.

\[ \begin{aligned} 12 = 2 \cdot 2 \cdot 3 \\ 16 = 2 \cdot 2 \cdot 2 \cdot 2 \end{aligned}\nonumber \]

Запишіть прості факторизації в компактній формі за допомогою експонентів.

\[ \begin{aligned} 12 = 2^2 \cdot 3^1 \\ 16 = 2^4 \end{aligned}\nonumber \]

Щоб знайти LCM, запишіть кожен фактор, який виявляється найвищою силою цього фактора, який з'являється. Фактори, які з'являються, - 2 і 3. Найвища потужність 2, яка з'являється, - 2 ⁴. Найвища потужність 3, яка з'являється, - 3 ¹.

\[ \begin{aligned} \text{LCM} = 2^4 \cdot 3^1 ~ & \textcolor{red}{ \text{ Keep highest power of each factor.}} \end{aligned}\nonumber \]

Тепер ми розгортаємо цей останній вираз, щоб отримати наш LCM.

\[ \begin{aligned} = 16 \cdot 3 ~ & \textcolor{red}{ \text{ Expand: } 2^4 = 16 \text{ and } 3^1 = 3.} \\ = 48. ~ & \textcolor{red}{ \text{ Multiply.}} \end{aligned}\nonumber \]

Зауважте, що ця відповідь ідентична LCM, знайденому в прикладі 8, який був знайдений шляхом перерахування кратних і вибору найменшого кратного спільного.

Вправа$\PageIndex{8}$

Використовуйте просту факторизацію, щоб знайти найменш спільний знаменник 18 і 24.

Відповідь: 72

Приклад$\PageIndex{10}$

Спростити:$\frac{5}{28} + \frac{11}{42}$.

Рішення

Простий множник знаменники в компактній формі з використанням експонент.

28 = 2 · 2 · ⁷⁼² · 7

42 = 2 · 3 · 7=2 ¹ · 3 ¹ · 7 ¹

Щоб знайти РК-дисплей, запишіть кожен фактор, який виявляється найвищою потужністю цього фактора, який з'являється. Факторами, які з'являються, є 2, 3 та 7. Найвища потужність 2, яка з'являється, - 2 ². Найвища потужність 3, яка з'являється, - 3 ¹. Найвища потужність 7, яка з'являється, - 7 ¹.

\[ \begin{aligned} \text{LCM} = 2^2 \cdot 3^1 \cdot 7^1 ~ & \textcolor{red}{ \text{ Keep highest power of each factor.}} \\ = 4 \cdot 3 \cdot 7 ~ & \textcolor{red}{ \text{ Expand: } 2^2 = 4, ~ 3^1 = 3, ~ 7^1 = 7.} \\ = 84 ~ & \textcolor{red}{ \text{ Multiply.}} \end{aligned}\nonumber \]

Створіть еквівалентні дроби з новим РК-дисплеєм, а потім додайте.

\[ \begin{aligned} \frac{5}{28} + \frac{11}{42} = \frac{5 \cdot \textcolor{red}{3}}{28 \cdot \textcolor{red}{3}} + \frac{11 \cdot \textcolor{red}{2}}{42 \cdot \textcolor{red}{2}} ~ & \textcolor{red}{ \text{ Equivalent fractions with LCD = 84.}} \\ = \frac{15}{84} + \frac{22}{84} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \\ = \frac{37}{84} ~ & \textcolor{red}{ \text{ Keep LCD; add numerators.}} \end{aligned}\nonumber \]

Вправа$\PageIndex{10}$

Спростити:$ \frac{5}{24} + \frac{5}{36}$

Відповідь: 25/72

Приклад$\PageIndex{11}$

Спростити:$- \frac{11}{24} - \frac{1}{18}$.

Рішення

Простий множник знаменники в компактній формі з використанням експонент.

24 = 2 · 2 · 2 · 3=2 ³ · 3 ¹

18 = 2 · 3 · 3=2 ¹ · 3 ²

Щоб знайти РК-дисплей, запишіть кожен фактор, який виявляється найвищою потужністю цього фактора, який з'являється. Фактори, які з'являються, - 2 і 3. Найвища потужність 2, яка з'являється, - 2 ³. Найвища потужність 3, яка з'являється, - 3 ².

\[ \begin{aligned} \text{LCM} = 2^3 \cdot 3^2 ~ & \textcolor{red}{ \text{ Keep highest power of each factor.}} \\ = 8 \cdot 9 ~ & \textcolor{red}{ \text{ Expand: } 2^3 = 8 \text{ and } 3^2 = 9.} \\ = 72. ~ & \textcolor{red}{ \text{ Multiply.}} \end{aligned}\nonumber \]

Створіть еквівалентні дроби за допомогою нового РК-дисплея, а потім відніміть.

\[ \begin{aligned} - \frac{11}{24} - \frac{1}{18} = - \frac{11 \cdot \textcolor{red}{3}}{24 \cdot \textcolor{red}{3}} - \frac{1 \cdot \textcolor{red}{4}}{18 \cdot \textcolor{red}{4}} ~ & \textcolor{red}{ \text{ Equivalent fractions with LCD = 72.}} \\ = - \frac{33}{72} - \frac{4}{72} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \\ = \frac{-33-4}{72} ~ & \textcolor{red}{ \text{ Keep LCD; subtract numerators.}} \\ = \frac{-37}{72} ~ & \textcolor{red}{ \text{ Simplify numerator.}} \end{aligned}\nonumber \]

Звичайно, негативний розділений на позитивний дає негативну відповідь, тому ми також можемо написати свою відповідь у формі

\[ - \frac{11}{24} - \frac{1}{18} = - \frac{37}{72}.\nonumber \]

Вправа$\PageIndex{11}$

Спростити:$ - \frac{5}{24} - \frac{11}{36}$

Відповідь: −37/72

Порівняння дробів

Найпростіший спосіб порівняння дробів - створення еквівалентних дробів.

Приклад$\PageIndex{12}$

Впорядкуйте дроби −1/2 та −4/5 на числовому рядку, а потім порівняйте їх за допомогою відповідного символу нерівності.

Рішення

Найменш спільний знаменник для 2 і 5 - це число 10. Спочатку зробіть еквівалентні дроби з РК-дисплеєм, рівним 10.

\[ \begin{array}{c} - \frac{1}{2} = - \frac{1 \cdot \textcolor{red}{5}}{2 \cdot \textcolor{red}{5}} = - \frac{5}{10} \\ - \frac{4}{5} = - \frac{4 \cdot \textcolor{red}{2}}{5 \cdot \textcolor{red}{2}} = - \frac{8}{10} \end{array}\nonumber \]

Для побудови десятих розділіть інтервал між −1 та 0 на десять рівних кроків.

$Знімок екрана 2019-08-30 о 9.06.17 PM.png$

Оскільки −4/5 лежить ліворуч від −1/2, ми маємо, що −4/5 менше −1/2, тому ми пишемо

\[ - \frac{4}{5} < - \frac{1}{2}.\nonumber \]

Вправа$\PageIndex{12}$

Порівняйте −3/8 і −1/2.

Відповідь: \[ - \frac{1}{2} < - \frac{3}{8}\nonumber \]

Вправи

У Вправи 1-10 перерахуйте кратні заданих чисел, а потім перерахуйте загальні кратні. Виберіть LCM зі списку загальних кратних.

1. 9 і 15

2. 15 і 20

3. 20 і 8

4. 15 і 6

5. 16 і 20

6. 6 і 10

7. 20 і 12

8. 12 і 8

9. 10 і 6

10. 10 і 12

У вправах 11-20 для заданих чисел обчислити НКМ за допомогою простої факторизації.

11. 54 і 12

12. 108 і 24

13. 18 і 24

14. 36 і 54

15. 72 і 108

16. 108 і 72

17. 36 і 24

18. 18 і 12

19. 12 і 18

20. 12 і 54

У Вправи 21-32 додайте або відніміть дроби, як зазначено, і спростіть свій результат.

21. $\frac{7}{12} − \frac{1}{12}$

22. $\frac{3}{7} − \frac{5}{7}$

23. $\frac{1}{9} + \frac{1}{9}$

24. $\frac{1}{7} + \frac{3}{7}$

25. $\frac{1}{5} − \frac{4}{5}$

26. $\frac{3}{5} − \frac{2}{5}$

27. $\frac{3}{7} − \frac{4}{7}$

28. $\frac{6}{7} − \frac{2}{7}$

29. $\frac{4}{11} + \frac{9}{11}$

30. $\frac{10}{11} + \frac{4}{11}$

31. $\frac{3}{11} + \frac{4}{11}$

32. $\frac{3}{7} + \frac{2}{7}$

У Вправи 33-56 додайте або відніміть дроби, як зазначено, і спростіть свій результат.

33. $\frac{1}{6} − \frac{1}{8}$

34. $\frac{7}{9} − \frac{2}{3}$

35. $\frac{1}{5} + \frac{2}{3}$

36. $\frac{7}{9} + \frac{2}{3}$

37. $\frac{2}{3} + \frac{5}{8}$

38. $\frac{3}{7} + \frac{5}{9}$

39. $\frac{4}{7} − \frac{5}{9}$

40. $\frac{3}{5} − \frac{7}{8}$

41. $\frac{2}{3} − \frac{3}{8}$

42. $\frac{2}{5} − \frac{1}{8$

43. $\frac{6}{7} − \frac{1}{6}$

44. $\frac{1}{2} − \frac{1}{4}$

45. $\frac{1}{6} + \frac{2}{3}$

46. $\frac{4}{9} + \frac{7}{8}$

47. $\frac{7}{9} + \frac{1}{8}$

48. $\frac{1}{6} + \frac{1}{7}$

49. $\frac{1}{3} + \frac{1}{7}$

50. $\frac{5}{6} + \frac{1}{4}$

51. $\frac{1}{2} − \frac{2}{7}$

52. $\frac{1}{3} − \frac{1}{8}$

53. $\frac{5}{6} − \frac{4}{5}$

54. $\frac{1}{2} − \frac{1}{9}$

55. $\frac{1}{3} + \frac{1}{8}$

56. $\frac{1}{6} + \frac{7}{9}$

У вправах 57-68 додайте або відніміть дроби, як зазначено, спочатку використовуючи просте факторизацію, щоб знайти найменш спільний знаменник.

57. $\frac{7}{36} + \frac{11}{54}$

58. $\frac{7}{54} + \frac{7}{24}$

59. $\frac{7}{18} − \frac{5}{12}$

60. $\frac{5}{54} − \frac{7}{12}$

61. $\frac{7}{36} + \frac{7}{54}$

62. $\frac{5}{72} + \frac{5}{108}$

63. $\frac{7}{24} − \frac{5}{36}$

64. $\frac{11}{54} + \frac{7}{72}$

65. $\frac{11}{12} + \frac{5}{18}$

66. $\frac{11}{24} + \frac{11}{108}$

67. $\frac{11}{54} − \frac{5}{24}$

68. $\frac{7}{54} − \frac{5}{24}$

У Вправи 69-80 додайте або відніміть дроби, як зазначено, і спростіть свій результат.

69. $\frac{−3}{7} + \left( \frac{−3}{7} \right)$

70. $\frac{−5}{9} + \left( \frac{−1}{9} \right)$

71. $\frac{7}{9} − \left( \frac{−1}{9} \right) $

72. $\frac{8}{9} − \left( \frac{−4}{9} \right)$

73. $\frac{7}{9} + \left( \frac{−2}{9} \right)$

74. $ \frac{2}{3} + \left( \frac{−1}{3} \right)$

75. $\frac{−3}{5} − \frac{4}{5}$

76. $\frac{−7}{9} − \frac{1}{9}$

77. $\frac{−7}{8} + \frac{1}{8}$

78. $\frac{−2}{3} + \(\frac{1}{3}$

79. $\frac{−1}{3} − \left( \frac{−2}{3} \right)$

80. $\frac{−7}{8} − \left( \frac{−5}{8} \right)$

У Вправи 81-104 додайте або відніміть дроби, як зазначено, і спростіть свій результат.

81. $\frac{−2}{7}$+\ гідророзриву {4} {5}\)

82. $\frac{−1}{4} + \frac{2}{7}$

83. $\frac{−1}{4} − \left( \frac{−4}{9} \right)$

84. $\frac{−3}{4} −left( \frac{−1}{8} \right)$

85. $\frac{−2}{7} + \frac{3}{4}$

86. $\frac{−1}{3} + \frac{5}{8}$

87. $\frac{−4}{9} − \frac{1}{3}$

88. $\frac{−5}{6} − \frac{1}{3}$

89. $\frac{−5}{7} − \left( \frac{−1}{5} \right)$

90. $\frac{−6}{7} − \left( \frac{−1}{8} \right)$

91. $\frac{1}{9} + \left( \frac{−1}{3} \right)$

92. $\frac{1}{8} + \left( \frac{−1}{2} \right)$

93. $\frac{2}{3} + \left( \frac{−1}{9} \right)$

94. $\frac{3}{4} + \left( \frac{−2}{3} \right)$

95. $\frac{−1}{2} + \left( \frac{−6}{7} \right)$

96. $\frac{−4}{5} + \left( \frac{−1}{2} \right)$

97. $\frac{−1}{2} + \left( \frac{−3}{4} \right)$

98. $\frac{−3}{5} + \left( \frac{−1}{2} \right)$

99. $\frac{−1}{4} − \frac{1}{2}$

100. $\frac{−8}{9} − \frac{2}{3}$

101. $\frac{5}{8} − \left( \frac{−3}{4} \right)$

102. $\frac{3}{4} − \left( \frac{−3}{8} \right)$

103. $\frac{1}{8} − \left( \frac{−1}{3} \right)$

104. $\frac{1}{2} − \left( \frac{−4}{9} \right)$

У вправах 105-120 складіть або відніміть дроби, як зазначено, і напишіть свою відповідь найнижчими термінами.

105. $\frac{1}{2} + \frac{3q}{5}$

106. $\frac{4}{7} − \frac{b}{3}$

107. $\frac{4}{9} − \frac{3a}{4}$

108. $\frac{4}{9} − \frac{b}{2}$

109. $\frac{2}{s} + \frac{1}{3}$

110. $\frac{2}{s} + \frac{3}{7}$

111. $\frac{1}{3} − \frac{7}{b}$

112. $\frac{1}{2} − \frac{9}{s}$

113. $\frac{4b}{7} + \frac{2}{3}$

114. $\frac{2a}{5} + \frac{5}{8}$

115. $\frac{2}{3} − \frac{9}{t}$

116. $\frac{4}{7} − \frac{1}{y}$

117. $\frac{9}{s} + \frac{7}{8}$

118. $\frac{6}{t} − \frac{1}{9}$

119. $\frac{7b}{8} − \frac{5}{9}$

120. $\frac{3p}{4} − \frac{1}{8}$

У вправах 121-132 визначте, яке з двох заданих тверджень вірно.

121. $\frac{−2}{3} < \frac{−8}{7}$або$\frac{− 2}{3} > \frac{−8}{7}$

122. $\frac{−1}{7} < \frac{−8}{9}$або$\frac{− 1}{7} > \frac{−8}{9}$

123. $\frac{6}{7} < \frac{7}{3}$або$\frac{6}{7} > \frac{7}{3}$

124. $\frac{1}{2} < \frac{2}{7}$або$\frac{1}{2} > \frac{2}{7}$

125. $\frac{−9}{4} < \frac{−2}{3}$або\ frac {− 9} {4} >\ гідророзриву {−2} {3}\)

126. $\frac{−3}{7} < \frac{−9}{2}$або$\frac{− 3}{7} > \frac{−9}{2}$

127. $\frac{5}{7} < \frac{5}{9}$або\ гідророзриву {5} {7} >\ гідророзриву {5} {9}\)

128. $\frac{1}{2} < \frac{1}{3}$або$\frac{1}{2} > \frac{1}{3}$

129. $\frac{−7}{2} < \frac{−1}{5}$або$\frac{− 7}{2} > \frac{−1}{5}$

130. $\frac{−3}{4} < \frac{−5}{9}$або$\frac{− 3}{4} > \frac{−5}{9}$

131. $\frac{5}{9} < \frac{6}{5}$або$\frac{5}{9} > \frac{6}{5}$

132. $\frac{3}{2} < \frac{7}{9}$або$\frac{3}{2} > \frac{7}{9}$

Відповіді

1. 45

3. 40

5. 80

7. 60

9. 30

11. 108

13. 72

15. 216

17. 72

19. 36

21. $\frac{1}{2}$

23. $\frac{2}{9}$

25. $\frac{−3}{5}$

27. $\frac{−1}{7}$

29. $\frac{13}{11}$

31. $\frac{7}{11}$

33. $\frac{1}{24}$

35. $\frac{13}{15}$

37. $\frac{31}{24}$

39. $\frac{1}{63}$

41. $\frac{7}{24}$

43. $\frac{29}{42}$

45. $\frac{5}{6}$

47. $\frac{65}{72}$

49. $\frac{10}{21}$

51. $\frac{3}{14}$

53. $\frac{1}{30}$

55. $\frac{11}{24}$

57. $\frac{43}{108}$

59. $\frac{−1}{36}$

61. $\frac{35}{108}$

63. $\frac{11}{72}$

65. $\frac{43}{36}$

67. $\frac{−1}{216}$

69. $\frac{−6}{7}$

71. $\frac{8}{9}$

73. $\frac{5}{9}$

75. $\frac{− 7}{5}$

77. $\frac{− 3}{4}$

79. $\frac{1}{3}$

81. $\frac{18}{35}$

83. $\frac{7}{36}$

85. $\frac{13}{28}$

87. $\frac{− 7}{9}$

89. $\frac{−18}{35}$

91. $\frac{− 2}{9}$

93. $\frac{5}{9}$

95. $\frac{−19}{14}$

97. $\frac{− 5}{4}$

99. $\frac{− 3}{4}$

101. $\frac{11}{8}$

103. $\frac{11}{24}$

105. $\frac{5+6 q}{10}$

107. $\frac{16 − 27 a}{36}$

109. $\frac{6 + s}{3 s}$

111. $\frac{b − 21}{3b}$

113. $\frac{12 b + 14}{21}$

115. $\frac{2 t − 27}{3t}$

117. $\frac{72 + 7 s}{8 s}$

119. $\frac{63 b − 40}{72}$

121. $\frac{− 2}{3} > \(\frac{− 8}{7}$

123. $\frac{6}{7} < \frac{7}{3}$

125. $\frac{− 9}{4} < \frac{− 2}{3}$

127. $\frac{5}{7} > \frac{5}{9}$

129. $\frac{− 7}{2 } < \frac{− 1}{5}$

131. $\frac{5}{9} < \frac{6}{5}$