1.2: Операції з дійсними числами

Last updated
Save as PDF

Page ID: 58261

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Перегляньте властивості дійсних чисел.
Спростіть вирази, що включають угруповання символів та експонентів.
Спростіть, використовуючи правильний порядок операцій.

Робота з дійсними числами

У цьому розділі ми продовжуємо розглядати властивості дійсних чисел і їх операції. Результат додавання дійсних чисел називається сумою ⁵³, а результат віднімання називається різницею ⁵⁴. Задані будь-які дійсні числа a, b і c, ми маємо такі властивості додавання:

Таблиця$\PageIndex{1}$
Властивість адитивної ідентичності: ⁵⁵	а+0=0+а=а
Адитивна зворотна властивість: ⁵⁶	a+ (−a) = (−a) +a=0
Асоціативна власність: ⁵⁷	(а+б) +с = а+ (б+с)
Комутаційна власність: ⁵⁸	а+б = б+а

Важливо відзначити, що додавання є комутативним, а віднімання - ні. Іншими словами, порядок, в якому ми додаємо, не має значення і дасть той же результат. Однак це не стосується віднімання.

$5+10=10+5$$5−10≠10−5$

$15=15$$−5≠5$

Ми використовуємо ці властивості, поряд з подвійно-негативною властивістю для дійсних чисел, для виконання більш задіяних послідовних операцій. Щоб спростити речі, складіть загальне правило спочатку замінити всі послідовні операції або додаванням або відніманням, а потім виконувати кожну операцію по порядку зліва направо.

Приклад$\PageIndex{1}$:

Спростити:$−10−(−10)+(−5)$.

Рішення

Замініть послідовні операції, а потім виконайте їх зліва направо.

$−10−(−10)+(−5)=−10+10−5$$\color{Cerulean}{Replace −(−) with addition (+)}$.

$\color{Cerulean}{Replace +(−) with subtraction (-).}$

$=0−5$

$=−5$

Відповідь

$−5$

Додавання або віднімання дробів вимагає спільного знаменника ⁵⁹. Припустимо, що спільний знаменник c є ненульовим цілим числом, і ми маємо

$\frac{a}{c}+\frac{b}{c}=\frac{a+b}{c}$і$\frac{a}{c}−\frac{b}{c}=\frac{a−b}{c}$

Приклад$\PageIndex{2}$:

Спростити:$\frac{2}{9}−\frac{1}{15}+\frac{8}{45}$.

Рішення

Спочатку визначте найменш загальне кратне (НКМ)$9, 15, and 45$. Найменш поширеним кратним всіх знаменників називається найменш спільний знаменник ⁶⁰ (РК). Почнемо з перерахування кратних кожному заданому знаменнику:

$\{9,18,27,36,45,54,63,72,81,90,\dots\}$$\color{Cerulean}{Multiples of 9}$

$\{15,30,45,60,75,90,\dots\}$$\color{Cerulean}{Multiples of 15}$

$\{45,90,135\dots\}$$\color{Cerulean}{Multiples of \: 45}$

Тут ми бачимо, що LCM$(9, 15, 45) = 45$. Помножте чисельник і знаменник кожного дробу на значення, які отримують еквівалентні дроби з визначеним спільним знаменником.

$\frac{2}{9}−\frac{1}{15}+\frac{8}{45}=\frac{2}{9}⋅\color{Cerulean}{\frac{5}{5}}$$−\frac{1}{15}⋅\color{Cerulean}{\frac{3}{3}}$$+\frac{8}{45}$

$=\frac{10}{45}−\frac{3}{45}+\frac{8}{45}$

Після того, як у нас є еквівалентні дроби, із загальним знаменником, ми можемо виконувати операції над чисельниками та записати результат над спільним знаменником.

$=\frac{10−3+8}{45}$

$=\frac{15}{45}$

А потім зменшити, якщо потрібно,

$=\frac{15\color{Cerulean}{÷15}}{45\color{Cerulean}{÷15}}$

$=\frac{1}{3}$

Відповідь

$\frac{1}{3}$

Пошук LCM за допомогою списків кратних, як описано в попередньому прикладі, часто буває дуже громіздким. Наприклад, спробуйте скласти список кратних для$12$ і$81$. Ми можемо впорядкувати процес знаходження НКМ, використовуючи прості множники.

$12=2^{2}⋅3$

$81=3^{4}$

Найменш поширеним кратним є добуток кожного простого коефіцієнта, піднятого до найвищої потужності. У цьому випадку

$LCM(12,81)=2^{2}⋅3^{4}=324$

Часто ми виявимо необхідність перекладу англійських речень, що передбачають додавання і віднімання до математичних тверджень. Нижче наведено кілька поширених перекладів.

$n+2 \color{Cerulean}{The\: sum\: of\: a\: number\: and\: 2.}$

$2−n \color{Cerulean}{The\: difference\: of\: 2\: and\: a\: number.}$

$n−2 \color{Cerulean}{Here\: 2\: is\: subtracted\: from\: a\: number.}$

Приклад$\PageIndex{3}$:

Що$8$ віднімається з суми$3$ і$\frac{1}{2}$?

Рішення

Ми знаємо, що віднімання не є комутаційним; тому ми повинні подбати про віднімання в правильному порядку. Спочатку додайте,$3$$\frac{1}{2}$ а потім відніміть$8$ наступним чином:

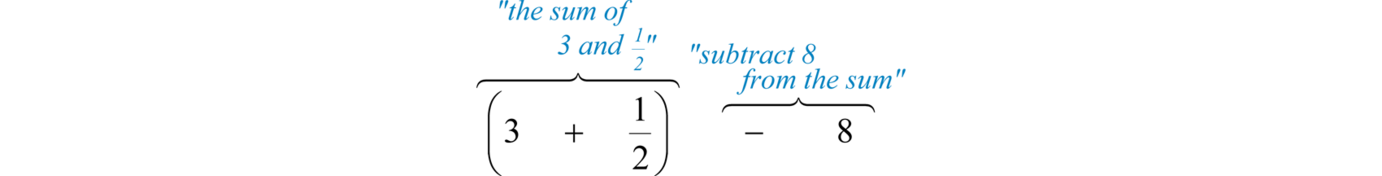
Виконайте зазначені операції.

$(3+\frac{1}{2})−8=(\frac{3}{1}⋅\color{Cerulean}{\frac{2}{2}}$$+\frac{1}{2})−8$

$=(\frac{6+1}{2})−8$

$=\frac{7}{2}−\frac{8}{1}⋅\color{Cerulean}{\frac{2}{2}}$

$=\frac{7−16}{2}$

$=−\frac{9}{2}$

Відповідь

$−\frac{9}{2}$

Результат множення дійсних чисел називається добутком ⁶¹ і результат ділення називається часткою ⁶². З огляду на будь-які дійсні числа a, b і c, ми маємо такі властивості множення:

Таблиця$\PageIndex{2}$
Нерухомість нульового фактора: ⁶³	а⋅0=0⋅а=0
Мультиплікативна ідентичність властивість: ⁶⁴	а⋅1=1⋅а=а
Асоціативна власність: ⁶⁵	(a⋅б) ⋅c = a⋅ (b⋅c)
Комутаційна власність: ⁶⁶	а⋅б=б⋅а

Важливо відзначити, що множення є комутативним, а ділення - ні. Іншими словами, порядок, в якому ми множимо, не має значення і дасть той же результат. Однак це не стосується поділу.

$5⋅10=10⋅5$$5÷10≠10÷5$

$50=50$$0.5≠2$

Ці властивості ми будемо використовувати для виконання послідовних операцій, пов'язаних з множенням і діленням. Нагадаємо, що добуток позитивного числа і негативного числа є негативним. Також добуток двох від'ємних чисел є додатним.

Приклад$\PageIndex{4}$:

Множення: 5 (−3) (−2) (−4).

Рішення

Помножте два числа одночасно наступним чином:

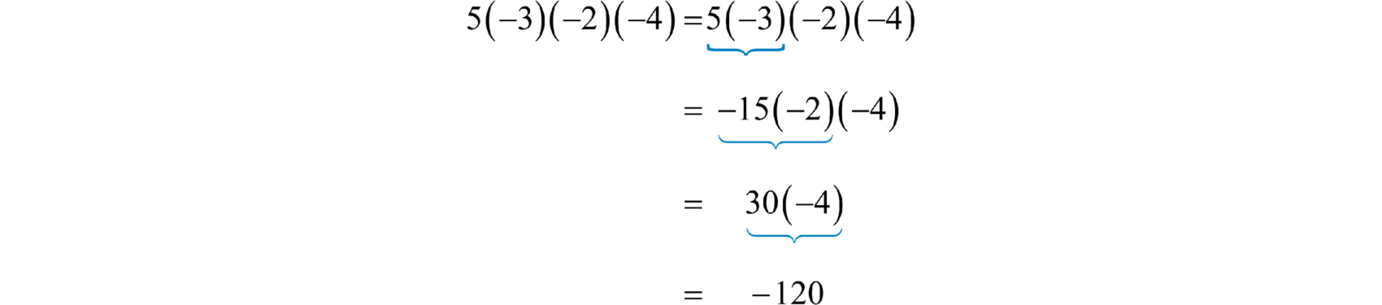
Відповідь

$−120$

Оскільки множення є комутативним, порядок, в якому ми множимо, не впливає на остаточну відповідь. Однак, коли послідовні операції передбачають множення та ділення, порядок має значення; отже, ми повинні працювати з операціями зліва направо, щоб отримати правильний результат.

Приклад$\PageIndex{5}$:

Спрощення: 10÷ (−2) (−5).

Рішення

Спочатку виконайте поділ, інакше результат буде невірним.

Зверніть увагу, що порядок, в якому ми множимо і ділимо, впливає на результат. Тому важливо виконувати операції множення і ділення в міру їх появи зліва направо.

Відповідь

$25$

Твір двох дробів - це дріб, утворений добутком чисельників і добутком знаменників. Іншими словами, для множення дробів множимо чисельники і множимо знаменники:

$\frac{a}{b}⋅\frac{c}{d}=\frac{ac}{bd}$

Приклад$\PageIndex{6}$:

Помножити$−\frac{4}{5}⋅\frac{25}{12}$.

Рішення

Множимо чисельники і множимо знаменники. Зменшити шляхом поділу будь-яких загальних факторів.

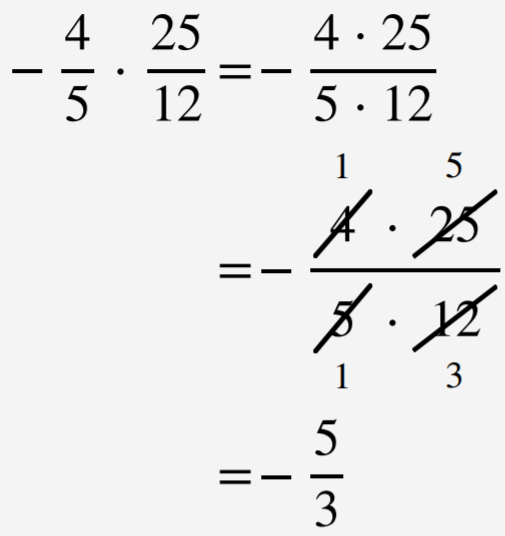Скріншот (133) .png — Малюнок$\PageIndex{4}$

Відповідь:

$−\frac{5}{3}$

Два дійсних числа, твір$1$ яких називається зворотними ⁶⁷. Тому$\frac{a}{b}$ і$\frac{b}{a}$ є взаємними тому що$\frac{a}{b}⋅\frac{b}{a}=\frac{ab}{ab}=1$. Наприклад,

$\frac{2}{3}⋅\frac{3}{2}=\frac{6}{6}=1$

Тому що їх продукт є$1, \frac{2}{3}$ і$\frac{3}{2}$ є взаємним. Деякі інші взаємні перелічені нижче:

$\frac{5}{8}$і$\frac{8}{5}$$7$ і$\frac{1}{7}$$−\frac{4}{5}$ і$−\frac{5}{4}$

Це визначення важливо, оскільки ділення дробів вимагає, щоб ви помножили дивіденд на зворотний дільник.

$\frac{a}{b}÷\color{Cerulean}{\frac{c}{d}}$$=\frac { \frac { a } { b } } { \frac { c } { d } } \cdot \color{OliveGreen}{\frac { \frac { d } { c } } { \frac { d } { c } }}$$=\frac { \frac { a } { b } \cdot \frac { d } { c } } { 1 } = \frac { a } { b } \cdot \color{Cerulean}{\frac { d } { c }}$

Загалом,

$\frac { a } { b } \div \color{Cerulean}{\frac { c } { d }}$$= \frac { a } { b } \cdot \color{Cerulean}{\frac { d } { c }}$$= \frac { a d } { b c }$

Приклад$\PageIndex{7}$:

Спростити:$\frac{5}{4}÷\frac{3}{5}⋅\frac{1}{2}$.

Рішення

Виконайте множення і ділення зліва направо.

$\frac{5}{4}÷\color{Cerulean}{\frac{3}{5}}$$⋅\frac{1}{2}=\frac{5}{4}⋅\color{Cerulean}{\frac{5}{3}}$$⋅\frac{1}{2}$

$=\frac{5⋅5⋅1}{4⋅3⋅2}$

$=\frac{25}{24}$

В алгебрі часто краще працювати з неправильними дробами. У цьому випадку залишаємо відповідь, виражену як неправильний дріб.

Відповідь

$\frac{25}{24}$

Вправа$\PageIndex{1}$

Спростити:$\frac{1}{2}⋅\frac{3}{4}÷\frac{1}{8}$.

Відповідь: $3$www.youtube.com/В/4ЗВ-ФЄПЗКК

Угруповання символів та експонентів

У обчисленні, де задіяно більше однієї операції, символи групування допомагають повідомити нам, які операції виконати в першу чергу. Символи групування ⁶⁸, які зазвичай використовуються в алгебрі, є:

$( )$$\color{Cerulean}{Parentheses}$

$[ ]$$\color{Cerulean}{Brackets}$

$\{ \}$$\color{Cerulean}{Braces}$

$-$$\color{Cerulean}{Fraction\: bar}$

Всі перераховані вище символи групування, а також абсолютне значення мають однаковий порядок пріоритету. Спочатку виконуйте операції всередині самого внутрішнього символу групування або абсолютного значення.

Приклад$\PageIndex{8}$:

Спростити:$2−(\frac{4}{5}−\frac{2}{15})$.

Рішення

Спочатку виконайте операції в дужках.

$2−(\frac{4}{5}−\frac{2}{15})= 2−(\frac{4}{5}⋅\color{Cerulean}{\frac{3}{3}}$$−\frac{2}{15})$

$=2−(\frac{12}{15}−\frac{2}{15})$

$=2−(\frac{10}{15})$

$=\frac{2}{1}⋅\color{Cerulean}{\frac{3}{3}}$$−\frac{2}{3}$

$=\frac{6-2}{3}$

$=\frac{4}{3}$

Відповідь:

$\frac{4}{3}$

Приклад$\PageIndex{9}$:

Спростити:$\frac { 5 - | 4 - ( - 3 ) | } { | - 3 | - ( 5 - 7 ) }$.

Рішення

Рядок дробу групує чисельник і знаменник. Значить, їх слід спростити окремо.

$\frac { 5 - | 4 - ( - 3 ) | } { | - 3 | - ( 5 - 7 ) } = \frac { 5 - | 4 + 3 | } { | - 3 | - ( - 2 ) }$

$= \frac { 5 - | 7 | } { | - 3 | + 2 }$

$= \frac { 5 - 7 } { 3 + 2 }$

$= \frac { - 2 } { 5 }$

$= - \frac { 2 } { 5 }$

Відповідь:

$−\frac{2}{5}$

Якщо число повторюється як множник багато разів, то можна записати твір в більш компактному вигляді, використовуючи експоненціальне позначення ⁶⁹. Наприклад,

$5⋅5⋅5⋅5=54$

База ⁷⁰ є множником, а додатне ціле значення експоненти ⁷¹ вказує кількість разів, коли база повторюється як множник. У наведеному вище$5$ прикладі база є, а показник -$4$. Експоненти іноді позначаються символом каретки (^), знайденим на клавіатурі,$5^4 = 5*5*5*5$. Загалом, якщо a - основа, яка повторюється як множник n разів, то

Коли експонента є,$2$ ми називаємо результат квадратом ⁷², а коли показник є,$3$ ми називаємо результат кубом ⁷³. Наприклад,

$5^{2}=5⋅5=25$$\color{Cerulean}{"5\: squared”}$

$5^{3}=5⋅5⋅5=125$$\color{Cerulean}{“5\: cubed”}$

Якщо показник більше ніж$3$, то читається позначення$a^{n}$ «а підвищений до n-й степені». Базою може бути будь-яке дійсне число,

$(2.5)^{2}=(2.5)(2.5)=6.25$

$(−\frac{2}{3})^{3}=(−\frac{2}{3})(−\frac{2}{3})(−\frac{2}{3})=−\frac{8}{27}$

$(−2)^4=(−2)(−2)(−2)(−2)=16$

$−2^{4}=−1⋅2⋅2⋅2⋅2=−16$

Зверніть увагу, що результат негативної бази з рівним показником позитивний. Результат негативної бази з непарним показником негативний. Ці факти часто плутають, коли беруть участь негативні числа. Уважно вивчіть наступні чотири приклади:

Таблиця$\PageIndex{3}$
*Підстава є$(−3)$.*	*Підстава є$3$.*
\ ((−3)\).» клас = "lt-математика-6227"> $(−3)^{4}=(−3)(−3)(−3)(−3)=+81$ $(−3)^{3}=(−3)(−3)(−3)=−27$	\ (3\).» клас = "lt-математика-6227"> $−3^{4}=−1⋅3⋅3⋅3⋅3=−81$ $−3^{3}=−1⋅3⋅3⋅3=−27$

У дужках вказується, що в якості основи слід використовувати від'ємне число.

Приклад$\PageIndex{10}$:

Розрахувати:

$(−\frac{1}{3})^{3}$
$(−\frac{1}{3})^{4}$

Рішення

$−\frac{1}{3}$Ось основа для обох проблем.

1. Використовуйте базу як фактор три рази.

$(−\frac{1}{3})^{3}=(−\frac{1}{3})(−\frac{1}{3})(−\frac{1}{3})$

$=−\frac{1}{27}$

2. Використовуйте базу як фактор чотири рази.

\ (−\ гідророзриву {1} {3}) ^ {4} = (−\ гідророзриву {1} {3}) (−\ гідророзриву {1} {3}) (−\ frac {1} {3}) (−\ frac {1} {3})

$=+\frac{1}{81}$

Відповіді:

−$\frac{12}{7}$
$\frac{1}{81}$

Вправа$\PageIndex{2}$

Спростити:

$−2^{4}$
$(−2)^{4}$

Відповідь

1. −16

2. 16

www.youtube.com/В/О3х52ПСРЖТГ

Порядок операцій

Коли в рамках розрахунку потрібно застосувати кілька операцій, ми повинні дотримуватися певного порядку, щоб забезпечити єдиний правильний результат.

Спочатку виконайте всі обчислення в найглибших дужках або символі групування.
Оцініть всі показники.
Застосовуємо множення і ділення зліва направо.
Виконайте всі операції додавання та віднімання останніми зліва направо.

Зверніть увагу, що множення і ділення повинні працювати зліва направо. Через це часто розумно виконувати ділення перед множенням.

Приклад$\PageIndex{11}$:

Спростити:$5^{3} − 24 ÷ 6 ⋅ \frac{1}{2} + 2.$

Рішення

Спочатку оцініть,$5^{3}$ а потім виконайте множення та ділення, коли вони з'являються зліва направо.

\ почати {вирівняні} 5 ^ {3} - 24\ div 6\ cdot\ frac {1} {2} + 2 & = 5 ^ {3} - 24\ div 6\ cdot\ frac {1} {2} {2} + 2\\\ & = 125 - 24\ div 6\ cdot\ frac {1} {2} + 2\\ & = 125 - 4\ cdot\ frac {1} {2} + 2\\ & = 125 - 2 + 2\\ & = 123 + 2\\ & = 125\ кінець {вирівняний}

Перше множення призвело б до неправильного результату.

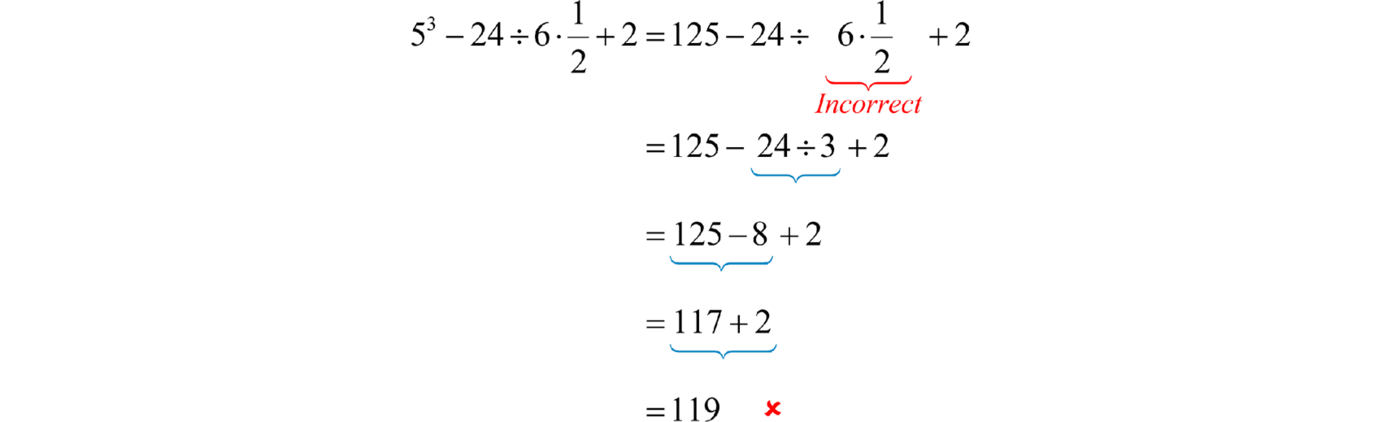
Відповідь:

$125$

Приклад$\PageIndex{12}$:

Спростити:$- 10 - 5 ^ { 2 } + ( - 3 ) ^ { 4 }$.

Рішення

Подбайте про те, щоб правильно визначити підставу при квадратурах.

$\begin{aligned} - 10 - 5 ^ { 2 } + ( - 3 ) ^ { 4 } & = - 10 - 25 + 81 \\ & = - 35 + 81 \\ & = 46 \end{aligned}$

Відповідь:

$46$

Ми рідше помилимося, якщо працюємо по одній операції за раз. Деякі проблеми можуть включати абсолютне значення, і в цьому випадку ми призначаємо йому той самий порядок пріоритету, що і дужки.

Приклад$\PageIndex{13}$:

Спростити:$7 - 5 \left| - 2 ^ { 2 } + ( - 3 ) ^ { 2 }\right.$.

Рішення

Почніть з виконання операцій в межах абсолютного значення спочатку.

$\begin{aligned} 7 - 5 \left| - 2 ^ { 2 } + ( - 3 ) ^ { 2 } \right| & = 7 - 5 | - 4 + 9 | \\ & = 7 - 5 | 5 | \\ & = 7 - 5 \cdot 5 \\ & = 7 - 25 \\ & = - 18 \end{aligned}$

Віднімання$7−5$ першого призведе до неправильних результатів.

Відповідь:

$−18$

Вправа$\PageIndex{3}$

Спростити:$- 6 ^ { 2 } - \left[ - 15 - ( - 2 ) ^ { 3 } \right] - ( - 2 ) ^ { 4 }$.

Відповідь

$-45$

www.youtube.com/В/ДНАВІКЗЛПА0

Ключові виноси

Додавання є комутативним, а віднімання - ні. Крім того, множення є комутативним, а ділення - ні.
Додавання або віднімання дробів вимагає спільного знаменника; множення або ділення дробів - ні.
Символи групування вказують, які операції потрібно виконати першими. Зазвичай ми групуємо математичні операції з дужками, дужками, дужками та рядком дробу. Ми також групуємо операції в межах абсолютних значень. Всі групи мають однаковий порядок пріоритету: операції всередині самого внутрішнього групування виконуються першими.
При використанні експоненціальних позначень$a^{n}$ база a використовується як множник n разів. Дужки вказують на те, що в якості основи слід використовувати від'ємне число. Наприклад,$(−5)^{2}$ є позитивним і$−5^{2}$ негативним.
Щоб забезпечити єдиний правильний результат при застосуванні операцій в рамках розрахунку, дотримуйтесь порядку операцій. Спочатку виконуйте операції в самих внутрішніх дужках або групуваннях. Далі спростіть всі експоненти. Виконуйте операції множення і ділення зліва направо. Нарешті, виконайте операції додавання і віднімання зліва направо.

Вправа$\PageIndex{4}$

Виконайте операції. Зменшіть всі дроби до найнижчих.

$33−(−15)+(−8)$
$−10−9+(−6)$
$−23+(−7)−(−10)$
$−1−(−1)−1$
$\frac{1}{2}+\frac{1}{3}−\frac{1}{6}$
$−\frac{1}{5}+\frac{1}{2}−\frac{1}{10}$
$\frac{2}{3}−(−\frac{1}{4})−\frac{1}{6}$
$−\frac{3}{2}−(−\frac{2}{9})−\frac{5}{6}$
$\frac{3}{4}−(−\frac{1}{2})−\frac{5}{8}$
$−\frac{1}{5}−\frac{3}{2}−(−\frac{7}{10})$
Відняти$3$ від$10$.
Відняти$−2$ від$16$.
Відняти$−\frac{5}{6}$ від$4$.
Відняти$−\frac{1}{2}$ від$\frac{3}{2}$.
Обчисліть суму$−10$ і$25$.
Обчисліть суму$−30$ і$−20$.
Знайдіть різницю$10$ і$5$.
Знайдіть різницю$−17$ і$−3$.

Відповідь

1. $40$

3. $−20$

5. $\frac{2}{3}$

7. $\frac{3}{4}$

9. $\frac{5}{8}$

11. $7$

13. $\frac{29}{6}$

15. $15$

17. $5$

Вправа$\PageIndex{5}$

Формула$d = | b − a |$ дає відстань між будь-якими двома точками на числовій лінії. Визначте відстань між заданими числами на числовому рядку.

$10$і$15$
$6$і$22$
$0$і$12$
$−8$і$0$
$−5$і$−25$
$−12$і$−3$

Відповідь

1. 5 одиниць

3. 12 одиниць

5. 20 одиниць

Вправа$\PageIndex{6}$

Визначте зворотне наступне.

$\frac{1}{3}$
$\frac{2}{5}$
$−\frac{3}{4}$
$−12$
$a$де$a ≠ 0$
$\frac{1}{a}$
$\frac{a}{b}$де$a ≠ 0$
$\frac{1}{ab}$

Відповідь

1. $3$

3. $−\frac{4}{3}$

5. $\frac{1}{a}$

7. $\frac{b}{a}$

Вправа$\PageIndex{7}$

Виконайте операції.

$−4 (−5) ÷ 2$
$(−15) (−3) ÷ (−9)$
$−22 ÷ (−11) (−2)$
$50 ÷ (−25) (−4)$
$\frac{2}{3} (−\frac{9}{10})$
$−\frac{5}{8} (−\frac{16}{25})$
$\frac{7}{6} (−\frac{6}{7})$
$−\frac{15}{9} (\frac{9}{5})$
$\frac{4}{5} (−\frac{2}{5}) ÷ \frac{16}{25}$
$(−\frac{9}{2}) (−\frac{3}{2}) ÷ \frac{27}{16}$
$\frac{8}{5} ÷ \frac{5}{2} ⋅ \frac{15}{40}$
$\frac{3}{16} ÷ \frac{5}{8} ⋅ \frac{1}{2}$
Знайдіть продукт$12$ і$7$.
Знайдіть продукт$−\frac{2}{3}$ і$12$.
Знайдіть частку$−36$ і$12$.
Знайдіть частку$−\frac{3}{4}$ і$9$.
Відняти$10$ від суми$8$ і$−5$.
Відняти$−2$ від суми$−5$ і$−3$.
Джо заробляє$$18.00$ на годину і «півтора часу» за кожну годину, яку він працює протягом декількох$40$ годин. Яка його оплата за$45$ години роботи на цьому тижні?
Біллі придбав$12$ пляшки води$$0.75$ за пляшку,$5$ фунти асорті цукерок$$4.50$ за фунт, і$15$ пакети мікрохвильового попкорну вартістю$$0.50$ кожного для своєї партії. Яким був його загальний рахунок?
Джеймс і Мері їздили додому з коледжу на свято Подяки. Вони розділили водіння, але Мері проїхала вдвічі далі, ніж Джеймс. Якщо Мері проїхала$210$ милі, то скільки миль пройшла вся поїздка?
$6 \frac{3}{4}$Дошку для ніг потрібно розрізати на$3$ шматочки однакової довжини. Якою буде довжина кожного шматка?
Студентка заробила$72, 78, 84,$ і$90$ бали на своїх перших чотирьох іспитах з алгебри. Яким був її середній бал тесту? (Нагадаємо, що середнє обчислюється шляхом додавання всіх значень у множині та ділення цього результату на кількість елементів у множині.)
Найхолодніша температура на Землі,$−129$° F, була зафіксована$1983$ на станції Восток, Антарктида. Найгарячіша температура на Землі,$136$° F, була зафіксована$1922$ в Аль-Азізії, Лівія. Обчисліть діапазон температур на Землі.

Відповідь

1. $10$

3. $−4$

5. $−\frac{3}{5}$

7. $−1$

9. $−\frac{1}{2}$

11. $\frac{6}{25}$

13. $84$

15. $−3$

17. $−7$

19. $$855$

21. $315$миль

23. $81$балів

Вправа$\PageIndex{8}$

Виконайте операції.

$7 − \{3 − [−6 − (10)]\}$
$− (9 − 12) − [6 − (−8 − 3)]$
$\frac{1}{2} \{5 − (10 − 3)\}$
$\frac{2}{3} \{−6 + (6 − 9)\}$
$5 \{2 [3 (4 − \frac{3}{2} )]\}$
$\frac{1}{2} \{−6 [− (\frac{1}{2} − \frac{5}{3})]\}$
$\frac { 5 - | 5 - ( - 6 ) | } { | - 5 | - | - 3 | }$
$\frac { | 9 - 12 | - ( - 3 ) } { | - 16 | - 3 ( 4 ) }$
$\frac { - | - 5 - ( - 7 ) | - ( - 2 ) } { | - 2 | + | - 3 | }$
$\frac { 1 - | 9 - ( 3 - 4 ) | } { - | - 2 | + ( - 8 - ( - 10 ) ) }$

Відповідь

1. $−1$2

3. $−1$

5. $75$

7. $−3$

9. $0$

Вправа$\PageIndex{9}$

Виконайте операції.

$12^{2}$
$(−12)^{2}$
$−12^{2}$
$−(−12)^{2}$
$−5^{4}$
$(−5)^{4}$
$(−\frac{1}{2})^{3}$
$−(−\frac{1}{2})^{3}$
$−(−\frac{3}{4})^{2}$
$−(−\frac{5}{2})^{3}$
$(−1)^{22}$
$(−1)^{13}$
$−(−1)^{12}$
$−(−1)^{5}$
$−10^{2}$
$−10^{4}$

Відповідь

1. $144$

3. $−144$

5. $−625$

7. $−\frac{1}{8}$

9. $−\frac{9}{16}$

11. $1$

13. $−1$

15. $−100$

Вправа$\PageIndex{10}$

Спростити.

$5 − 3 (4 − 3^{2})$
$8 − 5 (3 − 3^{2})$
$(−5)^{2} + 3 (2 − 4^{2})$
$6 − 2 (−5^{2} + 4 ⋅ 7)$
$5 − 3 [3 (2 − 3^{2}) + (−3)^{2}]$
$10 − 5 [(2 − 5)^{2} − 3]$
$[5^{2} − 3^{2} ] − [2 − (5 + (−4)^{2} )]$
$−7^{2} − [ (2 − 7)^{2} − (−8)^{2} ]$
$\frac{3}{16} ÷ (\frac{5}{12} −\frac{1}{2} +\frac{2}{3}) ⋅ 4$
$6 \cdot \left[ \left( \frac { 2 } { 3 } \right) ^ { 2 } - \left( \frac { 1 } { 2 } \right) ^ { 2 } \right] \div ( - 2 ) ^ { 2 }$
$\frac { 3 - 2 \cdot 5 + 4 } { 2 ^ { 2 } - 3 ^ { 2 } }$
$\frac { \left( 3 + ( - 2 ) ^ { 2 } \right) \cdot 4 - 3 } { - 4 ^ { 2 } + 1 }$
$\frac { - 5 ^ { 2 } + ( - 3 ) ^ { 2 } \cdot 2 - 3 } { 8 ^ { 2 } + 6 ( - 10 ) }$
$\frac { ( - 4 ) ^ { 2 } + ( - 3 ) ^ { 3 } } { - 9 ^ { 2 } - \left( - 12 + 2 ^ { 2 } \right) * 10 }$
$−5^{2} − 2 |−5| $
$−2^{4} + 6 | 2^{4} − 5^{2} |$
$− (4− | 7^{2} − 8^{2} |)$
$−3 (5 − 2 |−6|)$
$(−3)^{2}− | −2 + (−3)^{3} | − 4^{2}$
$−5^{2} − 2 | 3^{3} − 2^{4} | − (−2)^{5}$
$5 ⋅ |−5| − (2 − |−7|)^{3}$
$10^{2} + 2 ( |−5|^{3} − 6^{3})$
$\frac{2}{3} − | \frac{1}{2} − (−\frac{4}{3})^{2} |$
$−24 | \frac{10}{3} − \frac{1}{2} ÷ \frac{1}{5} |$
Обчислити суму квадратів перших трьох послідовних натуральних непарних чисел.
Обчисліть суму квадратів перших трьох послідовних натуральних чисел.
Що$6$ віднімається з суми квадратів$5$ і$8$?
Що$5$ віднімається з суми кубів$2$ і$3$?

Відповідь

1. $20$

3. $−17$

5. $41$

7. $35$

9. $\frac{9}{7}$

11. $\frac{3}{5}$

13. $−\frac{5}{2}$

15. $−35$

17. $11$

19. $−36$

21. $150$

23. $−\frac{11}{18}$

25. $35$

27. $83$

Вправа$\PageIndex{11}$

Що таке PEMDAS і чого його не вистачає?
Чи$0$ є у відповідь? Поясніть.
Поясніть, навіщо нам потрібен спільний знаменник для того, щоб додавати або віднімати дроби.
Поясніть$(−10)^{4}$, чому позитивний і$−10^{4}$ негативний.

Відповідь

1. Відповідь може відрізнятися

3. Відповідь може відрізнятися

Виноски

⁵³ Результат додавання.

⁵⁴ Результат віднімання.

^{55 Задано} будь-яке дійсне число$a, a + 0 = 0 + a = a$.

^{56 Задано} будь-яке дійсне число$a, a + (−a) = (−a) + a = 0$.

⁵⁷ Дано дійсні числа$a, b$ і$c, (a + b) + c = a + (b + c)$.

⁵⁸ Дано дійсні числа$a$ і$b$,$a + b = b + a$.

⁵⁹ Знаменник, який ділиться більш ніж одним дробом.

⁶⁰ Найменш поширений кратний набору знаменників.

⁶¹ Результат множення.

⁶² Результат ділення.

^{63 Задано} будь-яке дійсне число$a, a ⋅ 0 = 0 ⋅ a = 0 .$

^{64 Задано} будь-яке дійсне число$a, a ⋅ 1 = 1 ⋅ a = a .$

⁶⁵ Задано будь-які дійсні числа$a, b$ і$c, (a ⋅ b) ⋅ c = a ⋅ (b ⋅ c) . $

⁶⁶ Задано будь-які дійсні числа$a$ і$b, a ⋅ b = b ⋅ a.$

⁶⁷ Два дійсних числа, добуток яких є$1$.

⁶⁸ Дужки, дужки, фігурні дужки та рядок дробу є загальними символами, які використовуються для групування виразів та математичних операцій в рамках обчислення.

⁶⁹ Компактні позначення,$a^{n}$ що використовуються, коли коефіцієнт$a$ повторюється$n$ раз.

⁷⁰ Коефіцієнт$a$ в експоненціальному позначенні$a^{n}$.

⁷¹ натуральне число$n$ в експоненціальному позначенні$a^{n}$, яке вказує на кількість разів, коли база використовується як множник.

⁷² Результат, коли показник будь-якого дійсного числа дорівнює$2$.

⁷³ Результат, коли показник будь-якого дійсного числа дорівнює$3$.