7.6: Складні фракції

У цьому розділі ми дізнаємося, як спростити те, що називаються складними дробами, приклад яких слід.

\[\dfrac{\dfrac{1}{2}+\dfrac{1}{3}}{\dfrac{1}{4}+\dfrac{2}{3}}\]

Зауважимо, що і чисельник, і знаменник є проблемами дробів самі по собі, надаючи довіру тому, чому ми називаємо таку структуру як «складний дріб».

Є дві дуже різні методи, які ми можемо використовувати для спрощення складного дробу (1). Перша методика - це «природний» вибір.

Спрощення складних дробів — перша методика

Щоб спростити складний дріб, дійте наступним чином:

1. Спростити чисельник.
2. Спростити знаменник.
3. Спростити проблему поділу, яка залишається.

Давайте дотримуємося цього плану, щоб спростити складний дріб (1). Спочатку складіть дроби в чисельнику наступним чином.

\[\dfrac{1}{2}+\dfrac{1}{3}=\dfrac{3}{6}+\dfrac{2}{6}=\dfrac{5}{6}\]

По-друге, додайте дроби в знаменнику наступним чином.

\[\dfrac{1}{4}+\dfrac{2}{3}=\dfrac{3}{12}+\dfrac{8}{12}=\dfrac{11}{12}\]

Підставити результати з (2) і (3) на чисельник і знаменник (1) відповідно.

\[\dfrac{\dfrac{1}{2}+\dfrac{1}{3}}{\dfrac{1}{4}+\dfrac{2}{3}}=\dfrac{\dfrac{5}{6}}{\dfrac{11}{12}}\]

Права сторона (4) еквівалентна

\[\dfrac{5}{6} \div \dfrac{11}{12}\]

Це проблема поділу, тому інвертувати і помножити, коефіцієнт, потім скасувати загальні фактори.

\[\begin{aligned} \dfrac{\dfrac{1}{2}+\dfrac{1}{3}}{\dfrac{1}{4}+\dfrac{2}{3}} &=\dfrac{5}{6} \cdot \dfrac{12}{11} \\ &=\dfrac{5}{2 \cdot 3} \cdot \dfrac{2 \cdot 2 \cdot 3}{11} \\ &=\dfrac{5}{\not{2} \cdot \not{3}} \cdot \dfrac{\not{2} \cdot 2 \cdot \not{3}}{11} \\ &=\dfrac{10}{11} \end{aligned}\]

Ось схема роботи, від початку до кінця, представлена без коментарів. Це хороший шаблон для наслідування, виконуючи домашнє завдання.

\[\begin{aligned} \dfrac{\dfrac{1}{2}+\dfrac{1}{3}}{\dfrac{1}{4}+\dfrac{2}{3}} &=\dfrac{\dfrac{3}{6}+\dfrac{2}{6}}{\dfrac{3}{12}+\dfrac{8}{12}} \\ &=\dfrac{\dfrac{5}{6}}{\dfrac{11}{12}} \\ &=\dfrac{5}{6} \cdot \dfrac{12}{11} \\ &=\dfrac{5}{2 \cdot 3} \cdot \dfrac{2 \cdot 2 \cdot 3}{11}\\ &=\dfrac{5}{\not{2} \cdot \not{3}} \cdot \dfrac{\not{2} \cdot 2 \cdot \not{3}}{11} \\ &=\dfrac{10}{11} \end{aligned}\]

Тепер давайте розглянемо другий підхід до проблеми. Ми побачили, що спрощення чисельника в (2) вимагає спільного знаменника 6. Спрощення знаменника в (3) вимагало спільного знаменника 12. Отже, виберемо ще один спільний знаменник, цей спільний знаменник як для чисельника, так і для знаменника, а саме 12. Тепер помножте верх і низ (чисельник і знаменник) складного дробу (1) на 12 наступним чином.

\[\dfrac{\dfrac{1}{2}+\dfrac{1}{3}}{\dfrac{1}{4}+\dfrac{2}{3}}=\dfrac{\left(\dfrac{1}{2}+\dfrac{1}{3}\right) \color{blue}{12}}{\left(\dfrac{1}{4}+\dfrac{2}{3}\right) \color{blue}{12}}\]

Розподіліть 12 як в чисельнику, так і знаменнику і спростіть.

\[\dfrac{\left(\dfrac{1}{2}+\dfrac{1}{3}\right) \color{blue}{12}}{\left(\dfrac{1}{4}+\dfrac{2}{3}\right) \color{blue}{12}}=\dfrac{\left(\dfrac{1}{2}\right) \color{blue}{12}+\left(\dfrac{1}{3}\right) \color{blue}{12}}{\left(\dfrac{1}{4}\right) \color{blue}{12}+\left(\dfrac{2}{3}\right) \color{blue}{12}}=\dfrac{6+4}{3+8}=\dfrac{10}{11}\]

Давайте підсумуємо цю другу техніку.

Спрощення складних дробів — друга методика

Щоб спростити складний дріб, дійте наступним чином:

1. Знайдіть спільний знаменник як для чисельника, так і для знаменника.
2. Очистіть дроби з чисельника та знаменника, множивши кожен на загальний знаменник, знайдений на першому кроці.

Відзначимо, що для цієї конкретної проблеми другий спосіб набагато ефективніше. Це економить як простір, так і час і є більш естетичним. Це техніка, яку ми будемо надавати перевагу в решті цього розділу.

Давайте розглянемо інший приклад.

Приклад\(\PageIndex{1}\)

Використовуйте як Перший, так і Другий методи, щоб спростити вираз\[\dfrac{\dfrac{1}{x}-1}{1-\dfrac{1}{x^{2}}}\] State всі обмеження.

Рішення

Скористаємося першим прийомом, спрощуючи чисельник і знаменник окремо перед діленням. Спочатку зробіть еквівалентні дроби із загальним знаменником для задачі віднімання в чисельнику (7) та спростіть. Те ж саме виконайте для знаменника.

\[\dfrac{\dfrac{1}{x}-1}{1-\dfrac{1}{x^{2}}}=\dfrac{\dfrac{1}{x}-\dfrac{x}{x}}{\dfrac{x^{2}}{x^{2}}-\dfrac{1}{x^{2}}}=\dfrac{\dfrac{1-x}{x}}{\dfrac{x^{2}-1}{x^{2}}}\]

Далі інвертуйте і множте, потім коефіцієнт.

\[\dfrac{\dfrac{1}{x}-1}{1-\dfrac{1}{x^{2}}}=\dfrac{1-x}{x} \cdot \dfrac{x^{2}}{x^{2}-1}=\dfrac{1-x}{x} \cdot \dfrac{x^{2}}{(x+1)(x-1)}\]

Давайте викликаємо правило зміни знаків і заперечуємо дві частини дробу (1 − x) /x, чисельника та рядка дробу, а потім скасуємо загальні множники.

\[\dfrac{\dfrac{1}{x}-1}{1-\dfrac{1}{x^{2}}}=-\dfrac{x-1}{x} \cdot \dfrac{x^{2}}{(x+1)(x-1)}=-\dfrac{x-1}{\not{x}} \cdot \dfrac{x \not{x}}{(x+1)(x-1)}\]

Отже,

\[\dfrac{\dfrac{1}{x}-1}{1-\dfrac{1}{x^{2}}}=-\dfrac{x}{x+1}\]

Тепер спробуємо задачу вдруге, помноживши чисельник і знаменник на,\(x^2\) щоб очистити дроби як з чисельника, так і від знаменника.

\[\dfrac{\dfrac{1}{x}-1}{1-\dfrac{1}{x^{2}}}=\dfrac{\left(\dfrac{1}{x}-1\right) \color{blue}{x^{2}}}{\left(1-\dfrac{1}{x^{2}}\right)\color{blue}{x^{2}}}=\dfrac{\left(\dfrac{1}{x}\right) \color{blue}{x^{2}}-(1) \color{blue}{x^{2}}}{(1) \color{blue}{x^{2}}-\left(\dfrac{1}{x^{2}}\right) \color{blue}{x^{2}}}=\dfrac{x-x^{2}}{x^{2}-1}\]

Порядок чисельника останнього дробу вказує на те, що зміна знака була б корисною. Звести нанівець чисельник і дріб бар, множник, потім скасувати загальні множники.

\[\dfrac{\dfrac{1}{x}-1}{1-\dfrac{1}{x^{2}}}=-\dfrac{x^{2}-x}{x^{2}-1}=-\dfrac{x(x-1)}{(x+1)(x-1)}=-\dfrac{x(x-1)}{(x+1)(x-1)}=-\dfrac{x}{x+1}\]

Це точно така ж відповідь, що зустрічається з першою методикою. Щоб перерахувати обмеження, ми повинні переконатися, що ніякі значення х не роблять жодного знаменника рівним нулю, на початку завдання, в тілі нашої роботи або в остаточній відповіді.

У вихідній задачі, якщо x = 0, то обидва 1/x і\(1/x^{2}\) не визначені, тому x = 0 є обмеженням. У тілі нашої роботи множники x + 1 та x − 1, знайдені в різних знаменниках, складають x = −1 та x = 1 обмеження. Ніякі інші знаменники не постачають обмежень, які ще не були перераховані. Отже, для всіх x, відмінних від −1, 0 та 1, ліворуч

\[\dfrac{\dfrac{1}{x}-1}{1-\dfrac{1}{x^{2}}}=-\dfrac{x}{x+1}\]

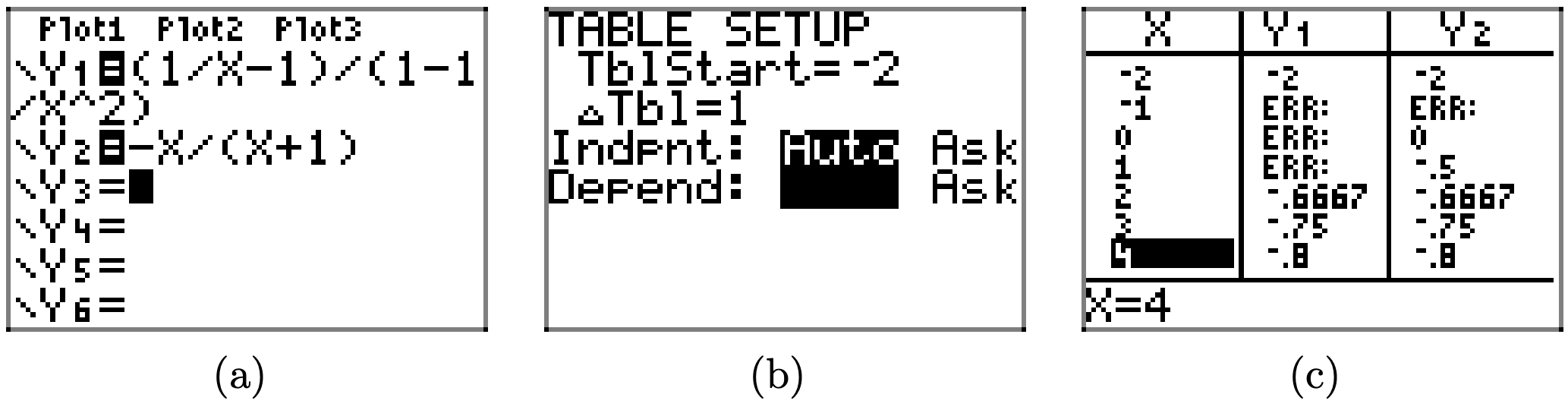
ідентична правій стороні. Знову ж таки, таблична утиліта калькулятора надає достатньо доказів цього факту на скріншотах, показаних на малюнку\(\PageIndex{1}\).

Зверніть увагу на повідомлення ERR (помилки) на кожному з обмежених значень x, але також зверніть увагу на ідеальну згоду Y1 і Y2 при всіх інших значеннях x.

Давайте розглянемо інший приклад, важливий приклад, який передбачає позначення функцій.

Малюнок\(\PageIndex{1}\). Використання функції таблиці графічного калькулятора для перевірки ідентичності в (8).

Приклад\(\PageIndex{2}\)

З огляду на це\[f(x)=\dfrac{1}{x}\], спростити вираз\[\dfrac{f(x)-f(2)}{x-2}\]. Перерахуйте всі обмеження.

Рішення

Пам'ятайте, f (2) означає підставити 2 на х, тому що f (x) = 1/x, ми знаємо, що f (2) = 1/2, тому

\[\dfrac{f(x)-f(2)}{x-2}=\dfrac{\dfrac{1}{x}-\dfrac{1}{2}}{x-2}\]

Щоб очистити дроби з чисельника, ми використаємо спільний знаменник 2x. У знаменнику немає дробів, які потребують очищення, тому загальний знаменник для чисельника і знаменника - 2х. Помножте чисельник і знаменник на 2x.

\[\dfrac{f(x)-f(2)}{x-2}=\dfrac{\left(\dfrac{1}{x}-\dfrac{1}{2}\right) \color{blue}{2x}}{(x-2) \color{blue}{2x}}=\dfrac{\left(\dfrac{1}{x}\right) \color{blue}{2x}-\left(\dfrac{1}{2}\right) \color{blue}{2x}}{(x-2) \color{blue}{2x}}=\dfrac{2-x}{2 x(x-2)}\]

Зведіть нанівець чисельник і дріб, а потім скасуйте загальні множники.

\[\dfrac{f(x)-f(2)}{x-2}=-\dfrac{x-2}{2 x(x-2)}=-\dfrac{x-2}{2 x(x-2)}=-\dfrac{1}{2 x}\]

У початковій задачі ми маємо знаменник x − 2, тому x = 2 є обмеженням. Якщо в тілі нашої роботи є дріб 1/x, який не визначено при x = 0, тому x = 0 також є обмеженням. Інші знаменники не передбачають інших обмежень. Отже, для всіх значень x, крім 0 і 2, ліва сторона

\[\dfrac{f(x)-f(2)}{x-2}=-\dfrac{1}{2 x}\]

ідентична правій стороні.

Давайте розглянемо інший приклад, що включає позначення функцій.

Приклад\(\PageIndex{3}\)

Дано\[f(x)=\dfrac{1}{x^{2}}\], спростити вираз\[\dfrac{f(x+h)-f(x)}{h}\] Перелічити всі обмеження.

Рішення

Функція позначення f (x + h) просить нас замінити кожен екземпляр x у формулі 1\(/ x^{2}\) на x + h\(f(x+h)=1 /(x+h)^{2}\).

Ось ще один спосіб подумати про цю підміну. Припустимо, що ми видаляємо х з

\[f(x)=\dfrac{1}{x^{2}}\]

щоб він читав

\[f( \space)=\dfrac{1}{( \space)^{2}}\]

Тепер, якщо ви хочете обчислити f (2), просто вставте 2 в порожню область між дужками. У нашому випадку ми хочемо обчислити f (x + h), тому ми вставляємо x + h у порожній простір між дужками в (12), щоб отримати

\[f(x+h)=\dfrac{1}{(x+h)^{2}}\]

Маючи на увазі ці попередні зауваження, повернемося до проблеми. Спочатку інтерпретуємо позначення функції як в наших попередніх зауваженнях і пишемо

\[\dfrac{f(x+h)-f(x)}{h}=\dfrac{\\(\begin{aligned} \dfrac{f(x+h)-f(x)}{h} &=\dfrac{x^{2}-\left(x^{2}+2 x h+h^{2}\right)}{h x^{2}(x+h)^{2}} \\ &=\dfrac{x^{2}-x^{2}-2 x h-h^{2}}{h x^{2}(x+h)^{2}} \\ &=\dfrac{-2 x h-h^{2}}{h x^{2}(x+h)^{2}} \end{aligned}\)frac{1}{(x+h)^{2}}-\dfrac{1}{x^{2}}}{h}\]

Загальний знаменник для чисельника знаходять шляхом перерахування кожного фактора до найвищої потужності, що він зустрічається. Значить, загальним знаменником є\(x^{2}(x+h)^{2}\). Знаменник не має дробів, що підлягають очищенню, тому досить помножити і чисельник, і знаменник на\(x^{2}(x+h)^{2}\).

\[\begin{aligned} \dfrac{f(x+h)-f(x)}{h} &=\dfrac{\left(\dfrac{1}{(x+h)^{2}}-\dfrac{1}{x^{2}}\right) \color{blue}{x^{2}(x+h)^{2}}}{h \color{blue}{x^{2}(x+h)^{2}}} \\ &=\dfrac{\left(\dfrac{1}{(x+h)^{2}}\right) \color{blue}{x^{2}(x+h)^{2}}-\left(\dfrac{1}{x^{2}}\right) \color{blue}{x^{2}(x+h)^{2}}}{h \color{blue}{x^{2}(x+h)^{2}}} \\ &=\dfrac{x^{2}-(x+h)^{2}}{h x^{2}(x+h)^{2}} \end{aligned}\]

Тепер ми розширимо чисельник. Не забудьте використовувати дужки і розподілити цей знак мінус.

\[\begin{aligned} \dfrac{f(x+h)-f(x)}{h} &=\dfrac{x^{2}-\left(x^{2}+2 x h+h^{2}\right)}{h x^{2}(x+h)^{2}} \\ &=\dfrac{x^{2}-x^{2}-2 x h-h^{2}}{h x^{2}(x+h)^{2}} \\ &=\dfrac{-2 x h-h^{2}}{h x^{2}(x+h)^{2}} \end{aligned}\]

Нарешті, множник a −h з чисельника в надії знайти загальний коефіцієнт для скасування.

\[\begin{aligned} \dfrac{f(x+h)-f(x)}{h} &=\dfrac{-h(2 x+h)}{h x^{2}(x+h)^{2}} \\ &=\dfrac{-\not{h}(2 x+h)}{\not{h} x^{2}(x+h)^{2}} \\ &=\dfrac{-(2 x+h)}{x^{2}(x+h)^{2}} \end{aligned}\]

Ми повинні зараз обговорити обмеження. У вихідному питанні (11) h в знаменнику не повинен дорівнювати нулю. Значить, h = 0 є обмеженням. У остаточному спрощеному вигляді коефіцієнт\(x^{2}\) в знаменнику не визначено, якщо х = 0. Отже, x = 0 є обмеженням. Нарешті, коефіцієнт\((x+h)^{2}\) у кінцевому знаменнику не визначено, якщо x+h = 0, тому x = −h є обмеженням. Решта знаменники не передбачають ніяких додаткових обмежень. Отже, передбачено\(h \neq 0, x \neq 0,\) і\(x \neq-h\), для всіх інших комбінацій x і h, ліва сторона

\[\dfrac{f(x+h)-f(x)}{h}=\dfrac{-(2 x+h)}{x^{2}(x+h)^{2}}\]

ідентична правій стороні.

Давайте розглянемо один остаточний приклад з використанням позначення функції.

Приклад\(\PageIndex{4}\)

Якщо\[f(x)=\dfrac{x}{x+1}\] спростити f (f (x)).

Рішення

Спочатку оцінюємо f в x, потім оцінюємо f в результаті першого обчислення. Таким чином, ми спочатку працюємо внутрішню функцію, щоб отримати

\[f(f(x))=f\left(\dfrac{x}{x+1}\right)\]

Позначення f (x/ (x + 1)) просить нас замінити кожне входження x у формулі x/ (x + 1) виразом x/ (x + 1). Заплутаний? Ось простий спосіб придумати цю заміну. Припустимо, що ми видаляємо х з

\[f(x)=\dfrac{x}{x+1}\]

замінюючи кожне входження x порожніми дужками, що призведе до створення шаблону

\[f(\space )=\dfrac{( \space)}{( \space)+1}\]

Тепер, якщо його попросять обчислити f (3), просто вставте 3 в порожні області між дужками. У цьому випадку ми хочемо обчислити f (x/ (x+ 1)), тому ми вставляємо x/ (x+ 1) в порожній простір між кожним набором дужок в (15), щоб отримати

\[f\left(\dfrac{x}{x+1}\right)=\dfrac{\dfrac{x}{x+1}}{\dfrac{x}{x+1}+1}\]

У нас тепер складний дріб. Загальним знаменником як для верхньої, так і для нижньої частини цього складного дробу є x + 1. Таким чином, множимо і чисельник, і знаменник нашого складного дробу на х + 1 і використовуємо розподільну властивість наступним чином.

\[\dfrac{\dfrac{x}{x+1}}{\dfrac{x}{x+1}+1}=\dfrac{\left(\dfrac{x}{x+1}\right)\color{blue}{(x+1)}}{\left(\dfrac{x}{x+1}+1\right)\color{blue}{(x+1)}}=\dfrac{\left(\dfrac{x}{x+1}\right)\color{blue}{(x+1)}}{\left(\dfrac{x}{x+1}\right)\color{blue}{(x+1)}+(1)\color{blue}{(x+1)}}\]

Скасувати і спростити.

\[\dfrac{\left(\dfrac{x}{x+1}\right)\color{blue}{(x+1)}}{\left(\dfrac{x}{x+1}\right)\color{blue}{(x+1)}+(1)\color{blue}{(x+1)}}=\dfrac{x}{x+(x+1)}=\dfrac{x}{2 x+1}\]

У кінцевому знаменнику значення x = −1/2 робить знаменник 2x + 1 рівним нулю. Отже, x = −1/2 є обмеженням. У тілі нашої роботи кілька дробів мають знаменники x + 1 і тому не визначені при x = −1. Таким чином, x = −1 є обмеженням. Ніякі інші знаменники не додають додаткових обмежень.

Отже, для всіх значень x, окрім x = −1/2 та x = −1, ліва сторона

\[f(f(x))=\dfrac{x}{2 x+1}\]

ідентична правій стороні.

Вправа

У вправах 1 - 6 оцініть функцію при заданому раціональному числі. Потім використовуйте перший або другий прийом для спрощення складних дробів, пояснених в оповіданні, щоб спростити вашу відповідь.

Вправа\(\PageIndex{1}\)

Враховується

\(f(x) = \frac{x+1}{2−x}\),

оцінювати і спрощувати\(f(\frac{1}{2})\).

Відповідь

1

Вправа\(\PageIndex{2}\)

Враховується

\(f(x) = \frac{2−x}{x+5}\),

оцінювати і спрощувати\(f(\frac{3}{2})\).

Вправа\(\PageIndex{3}\)

Враховується

\(f(x) = \frac{2x+3}{4−x}\),

оцінювати і спрощувати\(f(\frac{1}{3})\).

Відповідь

1

Вправа\(\PageIndex{4}\)

Враховується

\(f(x) = \frac{3−2x}{x+5}\)

оцінити і спростити\(f(\frac{2}{5})\)

Вправа\(\PageIndex{5}\)

Враховується

\(f(x) = \frac{5−2x}{x+4}\),

оцінювати і спрощувати\(f(\frac{3}{5})\).

Відповідь

\(\frac{19}{23}\)

Вправа\(\PageIndex{6}\)

Враховується

\(f(x) = \frac{2x−9}{11−x}\),

оцінювати і спрощувати\(f(\frac{4}{3})\).

У вправах 7 - 46 спростити дане складне раціональне вираження. Держави все є обмеженнями.

Вправа\(\PageIndex{7}\)

\(\frac{5+\frac{6}{x}}{\frac{25}{x}−\frac{36}{x^3}}\)

Відповідь

За умови\(x \ne 0, −\frac{6}{5}, or \frac{6}{5}\),

\(\frac{x^2}{5x−6}\).

Вправа\(\PageIndex{8}\)

\(\frac{7+\frac{9}{x}}{\frac{49}{x}−\frac{81}{x^3}}\)

Вправа\(\PageIndex{9}\)

\(\frac{\frac{7}{x−2}−\frac{5}{x−7}}{\frac{8}{x−7}+\frac{3}{x+8}}\)

Відповідь

За умови\(x \ne 2, 7, −8, or −\frac{43}{11}\),

\(\frac{(2x−39)(x+8)}{(11x+43)(x−2)}\)

Вправа\(\PageIndex{10}\)

\(\frac{\frac{9}{x+4}−\frac{7}{x−9}}{\frac{9}{x−9}+\frac{5}{x−4}}\)

Вправа\(\PageIndex{11}\)

\(\frac{3+\frac{7}{x}}{\frac{9}{x^2}−\frac{49}{x^4}}\)

Відповідь

За умови\(x \ne 0, −\frac{7}{3}, or \frac{7}{3}\),

\(\frac{x^3}{3x−7}\).

Вправа\(\PageIndex{12}\)

\(\frac{2−\frac{5}{x}}{\frac{4}{x^2}−\frac{25}{x^4}}\)

Вправа\(\PageIndex{13}\)

\(\frac{\frac{9}{x+4}+\frac{7}{x+9}}{\frac{9}{x+9}+\frac{2}{x−8}}\)

Відповідь

За умови\(x \ne −4, −9, 8, or \frac{54}{11}\),

\(\frac{(16x+109)(x−8)}{(11x−54)(x+4)}\)

Вправа\(\PageIndex{14}\)

\(\frac{\frac{4}{x−6}+\frac{9}{x−9}}{\frac{9}{x−6}+\frac{8}{x−9}}\)

Вправа\(\PageIndex{15}\)

\(\frac{\frac{5}{x−7}−\frac{4}{x−4}}{\frac{10}{x−4}−\frac{5}{x+2}}\)

Відповідь

За умови\(x \ne 7, 4, −2, or −8\),

\(\frac{x+2}{5(x−7)}\)

Вправа\(\PageIndex{16}\)

\(\frac{\frac{3}{x+6}+\frac{7}{x+9}}{\frac{9}{x+6}−\frac{4}{x+9}}\)

Вправа\(\PageIndex{17}\)

\(\frac{\frac{6}{x−3}+\frac{5}{x−8}}{\frac{9}{x−3}+\frac{7}{x−8}}\)

Відповідь

Надано\(x \ne 3, 8, or \frac{93}{16}\)

\(\frac{11x−63}{16x−93}\)

Вправа\(\PageIndex{18}\)

\(\frac{\frac{7}{x−7}−\frac{4}{x−2}}{\frac{7}{x−7}−\frac{6}{x−2}}\)

Вправа\(\PageIndex{19}\)

\(\frac{\frac{4}{x−2}+\frac{7}{x−7}}{\frac{5}{x−2}+\frac{2}{x−6}}\)

Відповідь

За умови\(x \ne 2, 7, or \frac{39}{7}\),

\(\frac{11x−42}{7x−39}\)

Вправа\(\PageIndex{20}\)

\(\frac{\frac{9}{x+2}−\frac{7}{x+5}}{\frac{4}{x+2}+\frac{3}{x+5}}\)

Вправа\(\PageIndex{21}\)

\(\frac{5+\frac{4}{x}}{\frac{25}{x}−\frac{16}{x^3}}\)

Відповідь

За умови\(x \ne 0, −\frac{4}{5}, or \frac{4}{5}\),

\(\frac{x^2}{5x−4}\).

Вправа\(\PageIndex{22}\)

\(\frac{\frac{6}{x+5}+\frac{5}{x+4}}{\frac{8}{x+5}−\frac{3}{x+4}}\)

Вправа\(\PageIndex{23}\)

\(\frac{\frac{9}{x−5}+\frac{8}{x+4}}{\frac{5}{x−5}−\frac{4}{x+4}}\)

Відповідь

За умови\(x \ne 5, −4, or −40\),

\(\frac{17x−4}{x+40}\).

Вправа\(\PageIndex{24}\)

\(\frac{\frac{4}{x−6}+\frac{4}{x−9}}{\frac{6}{x−6}+\frac{6}{x−9}}\)

Вправа\(\PageIndex{25}\)

\(\frac{\frac{6}{x+8}+\frac{5}{x−2}}{\frac{5}{x−2}−\frac{2}{x+2}}\)

Відповідь

За умови\(x \ne −8, 2, −2, or −\frac{14}{3}\),

\(\frac{(11x+28)(x+2)}{(3x+14)(x+8)}\).

Вправа\(\PageIndex{26}\)

\(\frac{\frac{7}{x+9}+\frac{9}{x−2}}{\frac{4}{x−2}+\frac{7}{x+1}}\)

Вправа\(\PageIndex{27}\)

\(\frac{\frac{7}{x+7}−\frac{5}{x+4}}{\frac{8}{x+7}−\frac{3}{x+4}}\)

Відповідь

За умови\(x \ne −7, −4, or −\frac{11}{5}\),

\(\frac{2x−7}{5x+11}\).

Вправа\(\PageIndex{28}\)

\(\frac{25−\frac{16}{x^2}}{5+\frac{4}{x}}\)

Вправа\(\PageIndex{29}\)

\(\frac{\frac{64}{x}−\frac{25}{x^3}}{8−\frac{5}{x}}\)

Відповідь

За умови\(x \ne 0 or \frac{5}{8}\),

\(\frac{8x+5}{x^2}\).

Вправа\(\PageIndex{30}\)

\(\frac{\frac{4}{x+2}+\frac{5}{x−6}}{\frac{7}{x−6}−\frac{5}{x+7}}\)

Вправа\(\PageIndex{31}\)

\(\frac{\frac{2}{x−6}−\frac{4}{x+9}}{\frac{3}{x−6​​​​​​​}−\frac{6}{x+9}}\)

Відповідь

За умови\(x \ne 6, −9, or 21\),

\(\frac{2}{3}\).

Вправа\(\PageIndex{32}\)

\(\frac{\frac{3}{x+6​​​​​​​}−\frac{4}{x+4}}{\frac{6}{x+6}−\frac{8}{x+4}}\)

Вправа\(\PageIndex{33}\)

\(\frac{\frac{9}{x^2}−\frac{64}{x^4}}{3−\frac{8}{x}}\)

Відповідь

За умови\(x \ne 0 or \frac{8}{3}\),

\(\frac{3x+8}{x^3}\).

Вправа\(\PageIndex{34}\)

\(\frac{\frac{9}{x^2}−\frac{25}{x^4}}{3−\frac{5}{x}}\)

Вправа\(\PageIndex{35}\)

\(\frac{\frac{4}{x−4​​​​​​​}−\frac{8}{x−7}}{\frac{4}{x−7}+\frac{2}{x+2}}\)

Відповідь

За умови\(x \ne 4, 7, −2, or 1\),

\(\frac{−2(x+2)}{3(x−4)}\).

Вправа\(\PageIndex{36}\)

\(\frac{2−\frac{7}{x}}{4−\frac{49}{x^2}}\)

Вправа\(\PageIndex{37}\)

\(\frac{\frac{3}{x^2+8x−9}+\frac{3}{x^2−81}}{\frac{9}{x^2−81}+\frac{9}{x^2−8x−9}}\)

Відповідь

За умови\(x \ne 1, −9, 9, −1, −5\),

\(\frac{(x−5)(x+1)}{3(x+5)(x−1)}\)

Вправа\(\PageIndex{38}\)

\(\frac{\frac{7}{x^2−5x−14}+\frac{2}{x^2−7x−18}}{\frac{5}{x^2−7x−18}+\frac{8}{x^2−6x−27}}\)

Вправа\(\PageIndex{39}\)

\(\frac{\frac{2}{x^2+8x+7}+\frac{5}{x^2+13x+42}}{\frac{7}{x^2+13x+42}+\frac{6}{x^2+3x−18}}\)

Відповідь

За умови\(x \ne −1, −7, −6, 3, −\frac{21}{13}\),

\(\frac{(7x+17)(x−3)}{(13x+21)(x+1)}\)

Вправа\(\PageIndex{40}\)

\(\frac{\frac{3}{x^2+5x−14}+\frac{3}{x^2−7x−98}}{\frac{3}{x^2−7x−98}+\frac{3}{x^2−15x+14}}\)

Вправа\(\PageIndex{41}\)

\(\frac{\frac{6}{x^2+11x+24}−\frac{6}{x^2+13+40}}{\frac{9}{x^2+13x+40}−{\frac{9}{x^2−3x−40}}\)

Відповідь

За умови\(x \ne −3, −8, −5, 8\),

\(\frac{−1(x−8)}{12(x+3)}\)

Вправа\(\PageIndex{42}\)

\(\frac{\frac{7}{x^2+19x+90}+\frac{7}{x^2+19x+90}}{\frac{9}{x^2+19x+90}+\frac{9}{x^2+7x−18}}\)

Вправа\(\PageIndex{43}\)

\(\frac{\frac{7}{x^2−6x+5}+\frac{7}{x^2+2x−35}}{\frac{8}{x^2+2x−35}+\frac{8}{x^2+8x+7}}\)

Відповідь

За умови\(x \ne 1, 5, −7, −1, 2\),

\(\frac{7(x+3)(x+1)}{8(x−2)(x−1)}\)

Вправа\(\PageIndex{44}\)

\(\frac{\frac{2}{x^2−4x−12​​​​​​​}−\frac{2}{x^2−x−30}}{\frac{2}{x^2−x−30}−\frac{2}{x^2−4x−45}}\)

Вправа\(\PageIndex{45}\)

\(\frac{\frac{4}{x^2 +6x−7​​​​​​​}−\frac{4}{x^2+2x−3}}{\frac{4}{x^2+2x−3}​−\frac{4}{x^2+5x+6}}\)

Відповідь

За умови\(x \ne −7, 1, −3, −2\),

\(\frac{−4(x+2)}{3(x+7)}\)

Вправа\(\PageIndex{46}\)

\(\frac{\frac{9}{x^2+3x−4}+\frac{8}{x^2−7x+6}}{\frac{4}{x^2−7x+6}+\frac{9}{x^2−10x+24}}\)

Вправа\(\PageIndex{47}\)

Враховуючи\(f(x) = \frac{2}{x}\), спростити

\(\frac{f(x)−f(3)}{x−3}\).

Вказати всі обмеження.

Відповідь

За умови\(x \ne 0, 3\),

\(\frac{−2}{3x}\)

Вправа\(\PageIndex{48}\)

Враховуючи\(f(x) = \frac{5}{x}\), спростити

\(\frac{f(x)−f(2)}{x−2}\).

Вказати всі обмеження.

Вправа\(\PageIndex{49}\)

Враховуючи\(f(x) = \frac{3}{x^2}\), спростити

\(\frac{f(x)−f(1)}{x−1}\).

Вказати всі обмеження.

Відповідь

За умови\(x \ne 0, 1\),

\(−\frac{3(x+1)}{x^2}\)

Вправа\(\PageIndex{50}\)

Враховуючи\(f(x) = \frac{5}{x^2}\), спростити

\(\frac{f(x)−f(2)}{x−2}\).

Вказати всі обмеження.

Вправа\(\PageIndex{51}\)

Враховуючи\(f(x) = \frac{7}{x}\), спростити

\(\frac{f(x+h)−f(x)}{h}\).

Вказати всі обмеження.

Відповідь

За умови\(x \ne 0, −h\), і\(h \ne 0\),

\(−\frac{7}{h(x+h)}\)

Вправа\(\PageIndex{52}\)

Враховуючи\(f(x) = \frac{4}{x}\), спростити

\(\frac{f(x+h)−f(x)}{h}\).

Вказати всі обмеження.

Вправа\(\PageIndex{53}\)

Враховується

\(f(x) = \frac{x+1}{3−x}\),

знайти і спростити\(f(\frac{1}{x})\). Вказати всі обмеження.

Відповідь

За умови\(x \ne 0, \frac{1}{3}\),

\(\frac{x+1}{3x−1}\)

Вправа\(\PageIndex{54}\)

Враховується

\(f(x) = \frac{2−x}{3x+4}\)

знайти і спростити\(f(\frac{2}{x})\). Вказати всі обмеження.

Вправа\(\PageIndex{55}\)

Враховується

\(f(x) = \frac{x+1}{2−5x}\),

знайти і спростити\(f(\frac{5}{x})\). Вказати всі обмеження.

Відповідь

За умови\(x \ne 0, \frac{25}{2}\),

\(\frac{x+5}{2x−25}\)

Вправа\(\PageIndex{56}\)

Враховується

\(f(x) = \frac{2x−3}{4+x}\),

знайти і спростити\(f(\frac{1}{x})\). Вказати всі обмеження.

Вправа\(\PageIndex{57}\)

Враховується

\(f(x) = \frac{x}{x+2}\),

знайти і спростити f (f (x)). Вказати всі обмеження.

Відповідь

За умови\(x \ne −2, −\frac{4}{3}\),

\(\frac{x}{3x+4}\)

Вправа\(\PageIndex{58}\)

Враховується

\(f(x) = \frac{2x}{x+5}\)

знайти і спростити f (f (x)). Вказати всі обмеження.

​​​​​​​