7.3: Графічні раціональні функції

Last updated
Save as PDF

Page ID: 58109

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Ми бачили, що знаменник раціональної функції ніколи не допускається рівним нулю; ділення на нуль не визначено. Так, при раціональних функціях існують особливі значення незалежної змінної, які мають особливе значення. Тепер не дивно, що поблизу значень, які роблять знаменник нулем, раціональні функції проявляють особливу поведінку, але тут ми також побачимо, що значення, які роблять нульовий чисельник, іноді створюють додаткову особливу поведінку в раціональних функціях.

Ми починаємо нашу дискусію з зосередження уваги на області раціональної функції.

Домен раціональної функції

При представленні з раціональною функцією форми

\[f(x)=\frac{a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n}}{b_{0}+b_{1} x+b_{2} x^{2}+\cdots+b_{m} x^{m}}\]

перше, що ми повинні зробити, це визначити домен. Рівнозначно, ми повинні визначити обмеження, значення незалежної змінної (зазвичай x), яких немає в домені. Щоб полегшити пошук обмежень, слід зарахувати знаменник раціональної функції (не завадить перерахувати чисельник і в цей час, як ми скоро побачимо). Після того, як домен встановлений і обмеження визначені, ось відповідні факти.

Поведінка раціональної функції при її обмеженнях

Раціональна функція може демонструвати лише одну з двох моделей поведінки при обмеженні (значення незалежної змінної, яка не знаходиться в області раціональної функції).

Графік раціональної функції матиме вертикальну асимптоту при обмеженому значенні.
Графік покаже «дірку» за обмеженим значенням.

У наступних двох прикладах ми розглянемо кожен із цих способів поведінки. У цьому першому прикладі ми бачимо обмеження, яке призводить до вертикальної асимптоти.

Приклад$\PageIndex{1}$

Намалюйте графік\[f(x)=\frac{1}{x+2}\]

Рішення

Насамперед необхідно визначити домен. Зауважте, що x = −2 робить знаменник f (x) = 1/ (x + 2) рівним нулю. Ділення на нуль не визначено. Отже, x = −2 не знаходиться в області f; тобто x = −2 є обмеженням. Рівнозначно, домен f є$\{x : x \neq-2\}$.

Тепер, коли ми визначили обмеження, ми можемо використовувати теорію розділу 7.1, щоб зрушити графік y = 1/x дві одиниці вліво, щоб створити графік$f(x) = 1/(x + 2)$, як показано на малюнку$\PageIndex{1}$.

Малюнок$\PageIndex{1}$. Функція f (x) = 1/ (x + 2) має обмеження при x = −2. Графік f має вертикальну асимптоту з рівнянням x = −2.

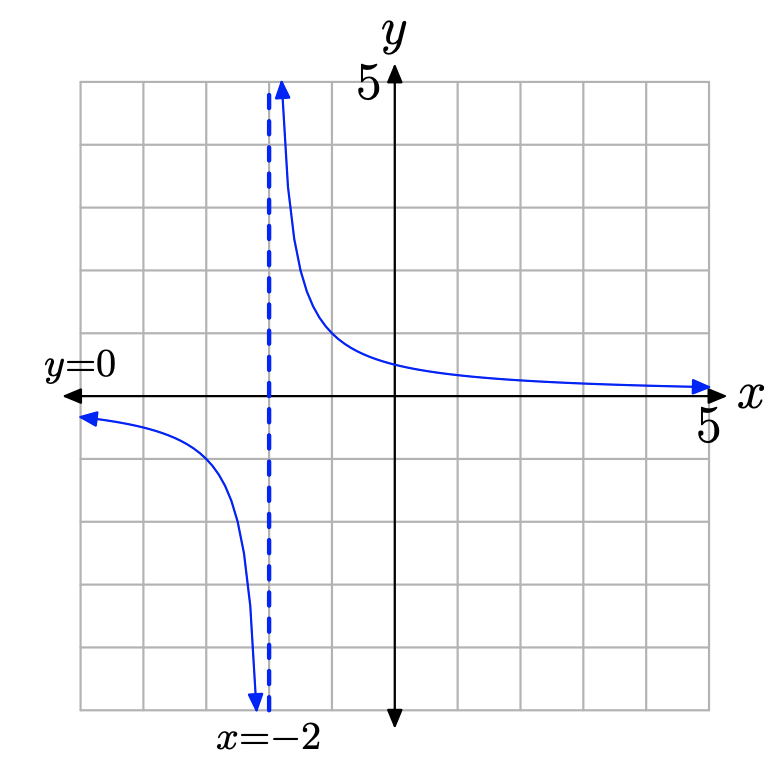
Функція f (x) = 1/ (x + 2) має обмеження при x = −2, а графік f демонструє вертикальну асимптоту, що має рівняння x = −2.

Важливо зазначити, що хоча обмежене значення x = −2 робить знаменник f (x) = 1/ (x + 2) рівним нулю, воно не робить чисельник рівним нулю. Скоро ми будемо більше сказати про це спостереження.

Давайте розглянемо приклад раціональної функції, яка демонструє «дірку» при одному з обмежених її значень.

Приклад$\PageIndex{2}$

Намалюйте графік\[f(x)=\frac{x-2}{x^{2}-4}\]

Рішення

Виділимо перший крок.

Факторні чисельники і знаменники

При роботі з раціональними функціями перше, що завжди слід зробити, це множник як чисельник, так і знаменник раціональної функції.

Дотримуючись цієї поради, ми враховуємо як чисельник, так і знаменник$f(x) = (x − 2)/(x^2 − 4)$.

\[f(x)=\frac{x-2}{(x-2)(x+2)}\]

Обмеження легше помітити, коли знаменник раціональної функції знаходиться в факторованій формі. Зрозуміло, що x = −2 і x = 2 зробить знаменник f (x) = (x−2)/(((x−2) (x+ 2)) рівним нулю. Отже, x = −2 і x = 2 є обмеженнями раціональної функції f.

Тепер, коли встановлені обмеження раціональної функції f, переходимо до другого кроку.

Знизити до найнижчих термінів

Після того, як ви встановите обмеження раціональної функції, друге, що вам слід зробити, це зменшити раціональну функцію до найнижчих показників.

Дотримуючись цієї поради, скасовуємо загальні чинники і зменшуємо раціональну функцію f (x) = (x − 2)/((x − 2) (x + 2)) до найнижчих, отримуючи нову функцію,

\[g(x)=\frac{1}{x+2}\]

Функції f (x) = (x − 2)/((x − 2) (x + 2)) та g (x) = 1/ (x + 2) не є однаковими функціями. Вони мають різні домени. Домен f є$D_{f}=\{x : x \neq-2,2\}$, але домен g є$D_{g}=\{x : x \neq-2\}$. Отже, єдина різниця між двома функціями виникає при x = 2. Число 2 знаходиться в домені g, але не в домені f.

Ми знаємо, як виглядає графік функції g (x) = 1/ (x + 2). Ми намалювали цей графік у$\PageIndex{1}$ прикладі і зображуємо його заново на малюнку$\PageIndex{2}$.

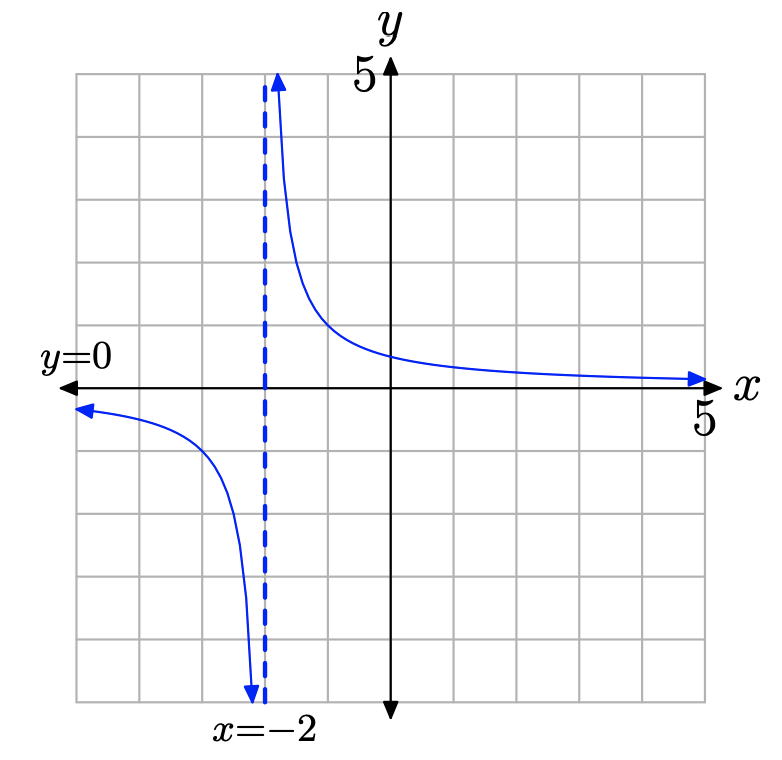
Знімок екрана 2019-07-12 в 4.53.48 PM.png — Малюнок$\PageIndex{2}$. Графік g (x) = 1/ (x + 2) демонструє вертикальну асимптоту при її обмеженні x = −2.

Складність, з якою ми зараз стикаємося, полягає в тому, що нас попросили намалювати графік f, а не графік g Однак ми знаємо, що функції f і g узгоджуються у всіх значеннях x, крім x = 2. Якщо видалити це значення з графа g, то у нас буде графік f.

Отже, який момент слід прибрати з графіка g? Ми повинні видалити точку, яка має значення x, рівне 2. Тому оцінюємо функцію g (x) = 1/ (x + 2) при x = 2 і знаходимо\[g(2)=\frac{1}{2+2}=\frac{1}{4}\]

Оскільки g (2) = 1/4, знімаємо точку (2, 1/4) з графіка g для отримання графіка f. результат показаний на рис$\PageIndex{3}$.

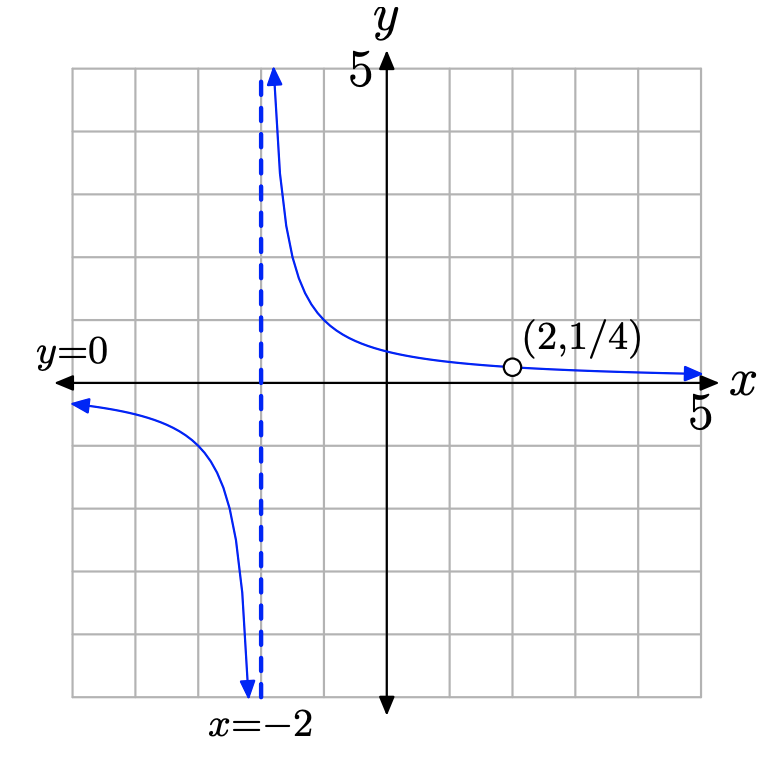
Знімок екрана 2019-07-12 в 4.55,14 PM.png — Малюнок$\PageIndex{3}$. Графік f (x) = (x − 2)/((x − 2) (x + 2)) демонструє вертикальну асимптоту при її обмеженні x = −2 та дірку при другому обмеженні x = 2.

Ми робимо паузу, щоб зробити важливе спостереження. У$\PageIndex{2}$ прикладі ми почали з функції

\[f(x)=\frac{x-2}{(x-2)(x+2)}\]

який мав обмеження на x = 2 та x = −2. Після зменшення функція

\[g(x)=\frac{1}{x+2}\]

більше не мав обмеження при х = 2. Функція g мала єдине обмеження при x = −2. Результатом, як видно на малюнку$\PageIndex{3}$, стала вертикальна асимптота при залишковому обмеженні та діра на обмеженні, яка «пішла» через скасування. Це призводить нас до наступної процедури.

Асимптота або Отвір?

Щоб визначити, чи має графік раціональної функції вертикальну асимптоту або дірку при обмеженні, діряють наступним чином:

Коефіцієнтний чисельник та знаменник початкової раціональної функції f Визначити обмеження f.
Звести раціональну функцію до найнижчих членів, назвавши нову функцію g Визначити обмеження функції g.
Ті обмеження f, які залишаються обмеженнями функції g, введуть вертикальні асимптоти в граф f.
Ті обмеження f, які більше не є обмеженнями функції g, введуть «дірки» в граф f Для визначення координат отворів підставляють кожне обмеження f, що не є обмеженням g, у функцію g для визначення y-значення дірки.

Тепер звернемо увагу на нулі раціональної функції.

Нулі раціональної функції

Ми бачили, що поділ на нуль не визначено. Тобто, якщо у нас дріб N/D, то D (знаменник) не повинен дорівнювати нулю. Таким чином, 5/0, −15/0 і 0/0 не визначені. З іншого боку, в дробі N/D, якщо N = 0 а$D \neq 0$, то дріб дорівнює нулю. Наприклад, 0/5, 0/ (−15) і 0$/ \pi$ дорівнюють нулю.

Тому при роботі з довільною раціональною функцією, такою як

\[f(x)=\frac{a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n}}{b_{0}+b_{1} x+b_{2} x^{2}+\cdots+b_{m} x^{m}}\]

будь-яке значення x, яке зробить чисельник нулем без одночасного внесення знаменника рівним нулю, буде нулем раціональної функції f.

Це обговорення призводить до наступної процедури ідентифікації нулів раціональної функції.

Пошук нулів раціональних функцій

Щоб визначити нулі раціональної функції, дійте наступним чином.

Коефіцієнт як чисельника, так і знаменника раціональної функції f.
Визначити обмеження раціональної функції f.
Визначте значення незалежної змінної (зазвичай x), які роблять чисельник рівним нулю.
Нулями раціональної функції f будуть ті значення x, які роблять чисельник нулем, але не є обмеженнями раціональної функції f.

Давайте розглянемо приклад.

Приклад$\PageIndex{3}$

Знайти нулі раціональної функції, визначеної\[f(x)=\frac{x^{2}+3 x+2}{x^{2}-2 x-3}\]

Рішення

Коефіцієнтний чисельник і знаменник раціональної функції f.

\[f(x)=\frac{(x+1)(x+2)}{(x+1)(x-3)}\]

Значення x = −1 і x = 3 роблять знаменник рівним нулю і є обмеженнями.

Далі зауважте, що x = −1 і x = −2 роблять чисельник рівним нулю. Однак x = −1 також є обмеженням раціональної функції f, тому вона не буде нулем f, з іншого боку, значення x = −2 не є обмеженням і буде нулем f.

Хоча ми правильно визначили нулі f, це повчально перевірити значення х, які роблять чисельник f дорівнює нулю. Якщо ми підставимо x = −1 у вихідну функцію, визначену рівнянням (6), ми виявимо, що

\[f(-1)=\frac{(-1)^{2}+3(-1)+2}{(-1)^{2}-2(-1)-3}=\frac{0}{0}\]

не визначено. Отже, x = −1 не є нулем раціональної функції f. Складність у цьому випадку полягає в тому, що x = −1 також робить знаменник рівним нулю.

З іншого боку, коли ми підставляємо x = −2 у функцію, визначену рівнянням (6),

\[f(-2)=\frac{(-2)^{2}+3(-2)+2}{(-2)^{2}-2(-2)-3}=\frac{0}{5}=0\]

У цьому випадку x = −2 робить чисельник рівним нулю, не роблячи знаменник рівним нулю. Отже, x = −2 є нулем раціональної функції f.

Важливо відзначити, що ви повинні працювати з початковою раціональною функцією, а не її зменшеною формою, при визначенні нулів раціональної функції.

Приклад$\PageIndex{4}$

Визначте нулі раціональної функції\[f(x)=\frac{x^{2}-6 x+9}{x^{2}-9}\]

Рішення

Фактор як чисельник, так і знаменник. \[f(x)=\frac{(x-3)^{2}}{(x+3)(x-3)}\]

Зауважте, що x = −3 і x = 3 є обмеженнями. Далі єдине значення х, яке зробить чисельник рівним нулю - х = 3. Однак це теж обмеження. Значить, функція f не має нулів.

Справа тут полягає в тому, що станеться, якщо ви працюєте зі зменшеною формою раціональної функції при спробі знайти її нулі. Скасування подібних факторів призводить до нової функції,

\[g(x)=\frac{x-3}{x+3}\]

Зауважте, що g має лише одне обмеження, x = −3. Далі х = 3 робить чисельник g рівним нулю і не є обмеженням. Значить, x = 3 - це нуль функції g, але він не є нулем функції f.

Цей приклад демонструє, що ми повинні ідентифікувати нулі раціональної функції, перш ніж скасувати загальні фактори.

Креслення графіка раціональної функції

У цьому розділі ми будемо використовувати нулі та асимптоти раціональної функції, щоб допомогти намалювати графік раціональної функції. Ми також досліджуємо кінцеву поведінку раціональних функцій. Почнемо з прикладу.

Приклад$\PageIndex{5}$

Намалюйте графік раціональної функції\[f(x)=\frac{x+2}{x-3}\]

Рішення

По-перше, зверніть увагу, що і чисельник, і знаменник вже враховані. Функція має одне обмеження, x = 3. Далі зауважте, що x = −2 робить чисельник рівняння (9) нулем і не є обмеженням. Отже, x = −2 є нулем функції. Нагадаємо, що функція дорівнює нулю, де її графік перетинає горизонтальну вісь. Отже, графік f перетинає вісь x в (−2, 0), як показано на малюнку$\PageIndex{4}$.

Зауважте, що раціональна функція (9) вже зведена до найнижчих. Отже, обмеження при x = 3 розмістить вертикальну асимптоту при x = 3, що також показано на малюнку$\PageIndex{4}$.

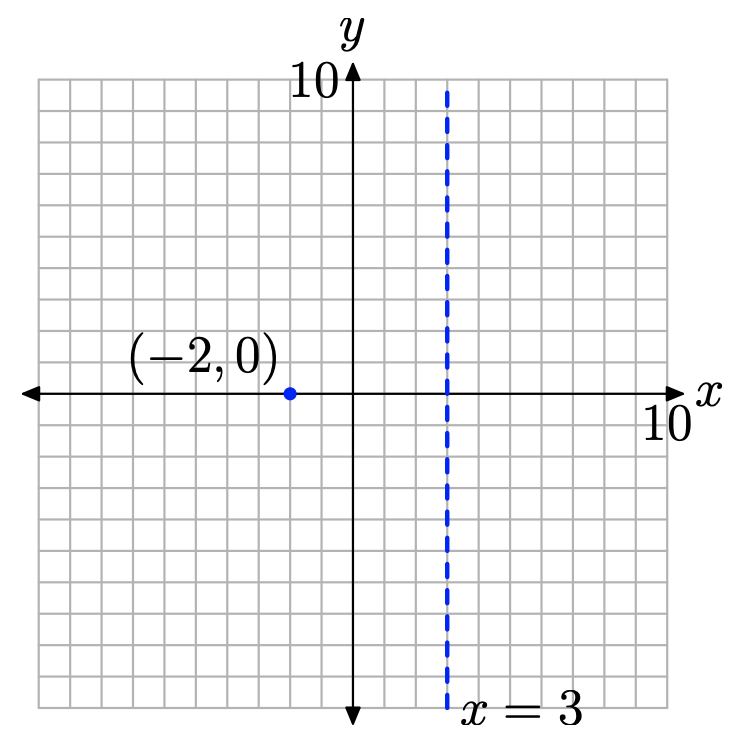
Знімок екрана 2019-07-12 в 6.15.35 PM.png — Малюнок$\PageIndex{4}$. Побудувати і позначити X-перехоплення і вертикальну асимптоту.

На даний момент ми знаємо дві речі:

Графік перетинає вісь x за адресою (−2, 0).
На кожній стороні вертикальної асимптоти при x = 3 може статися одна з двох речей. Або графік підніметься до позитивної нескінченності, або графік впаде до негативної нескінченності.

Щоб виявити поведінку біля вертикальної асимптоти, давайте побудуємо одну точку на кожній стороні вертикальної асимптоти, як показано на малюнку$\PageIndex{5}$.

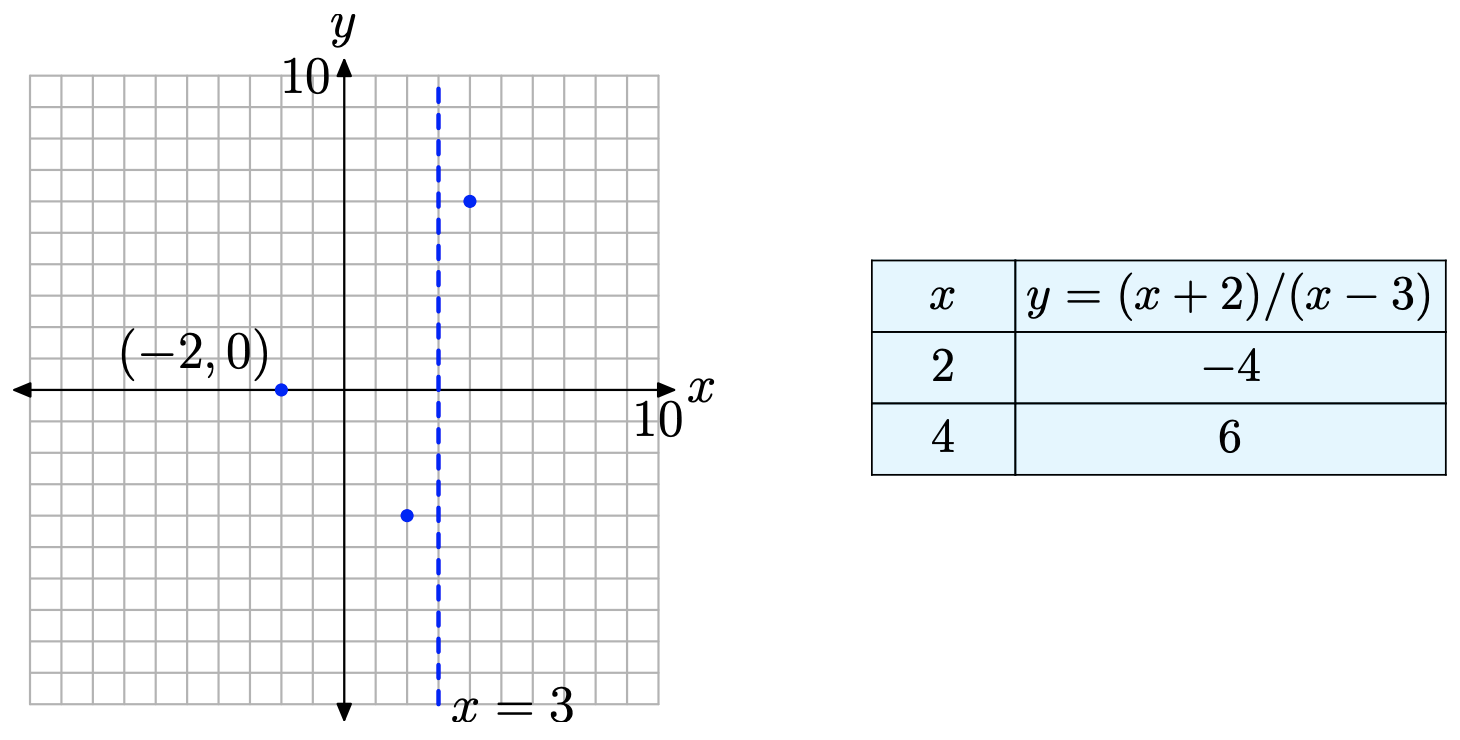
Знімок екрана 2019-07-12 в 6.17.45 PM.png — Малюнок$\PageIndex{5}$. Додаткові точки допомагають визначити поведінку поблизу вертикальної асимптоти.

Розглянемо праву сторону вертикальної асимптоти і нанесену точку (4, 6), через яку повинен пройти наш графік. Коли графік наближається до вертикальної асимптоти при x = 3, може статися лише одна з двох речей. Або графік піднімається до позитивної нескінченності, або графік падає до негативної нескінченності. Однак для того, щоб останнє сталося, графік повинен спочатку пройти через точку (4, 6), потім перетнути вісь x між x = 3 і x = 4 на її спуску до мінус нескінченності. Але ми вже знаємо, що єдиний x-перехоплення знаходиться в точці (2, 0), тому цього не може статися. Значить, праворуч графік повинен пройти через точку (4, 6), потім піднятися до позитивної нескінченності, як показано на малюнку$\PageIndex{6}$.

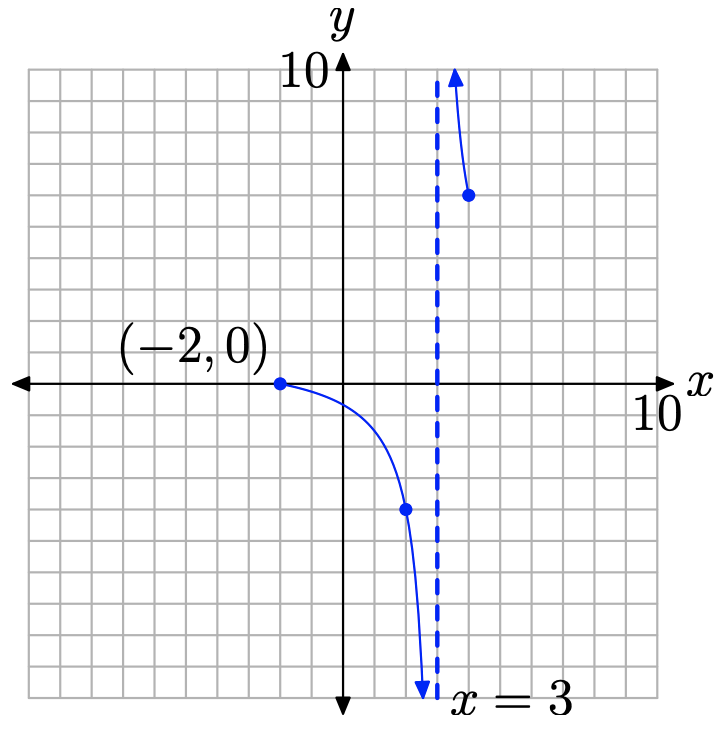
Знімок екрана 2019-07-12 в 6.19.13 PM.png — Малюнок$\PageIndex{6}$. Поведінка біля вертикальної асимптоти.

Аналогічний аргумент тримається зліва від вертикальної асимптоти при x = 3. Графік не може пройти через точку (2, −4) і підніматися до позитивної нескінченності, коли він наближається до вертикальної асимптоти, оскільки для цього потрібно, щоб він перетинав вісь x між x = 2 та x = 3. Однак для цієї мети в цьому регіоні немає перехоплення x-перехоплення. Отже, ліворуч графік повинен пройти через точку (2, −4) і впасти до негативної нескінченності, коли він наближається до вертикальної асимптоти при x = 3. Така поведінка показано на рис$\PageIndex{6}$.

Нарешті, як щодо кінцевої поведінки раціональної функції? Що відбувається з графіком раціональної функції, коли x збільшується без обмежень? Що відбувається, коли x зменшується без прив'язки? Одним з простих способів відповісти на ці питання є використання таблиці для дослідження поведінки чисельно. Графічний калькулятор полегшує це завдання.

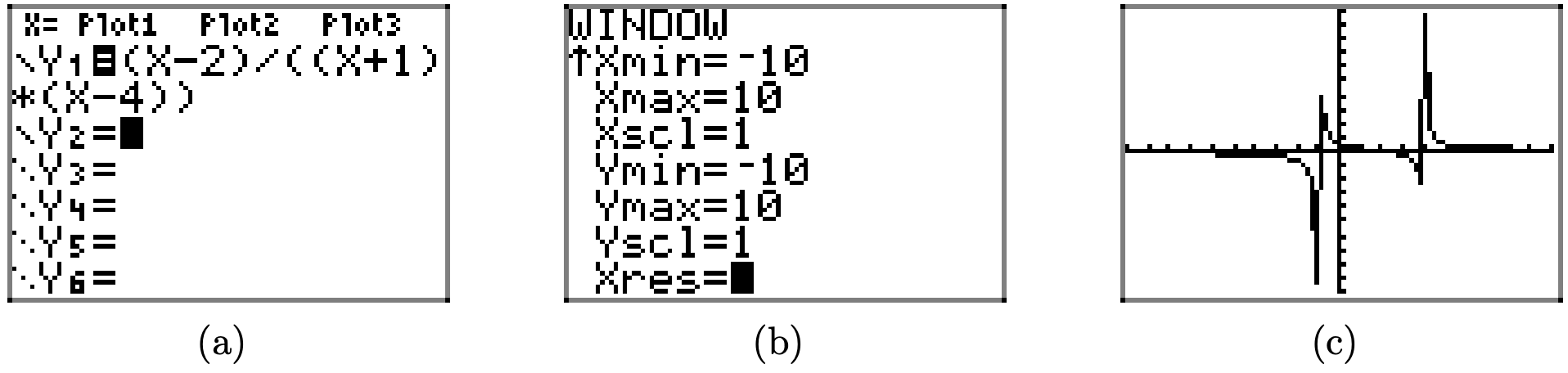
Спочатку введіть функцію, як показано на малюнку$\PageIndex{7}$ (a), потім натисніть 2nd TBLSET, щоб відкрити вікно, показане на малюнку$\PageIndex{7}$ (b). Для того, що ми збираємося зробити, всі налаштування в цьому вікні не мають значення, збережіть один. Переконайтеся, що ви використовуєте клавіші зі стрілками, щоб виділити ASK для змінної Indpnt (незалежна) і натисніть клавішу ENTER, щоб вибрати цей параметр. Нарешті, виберіть 2-у ТАБЛИЦЮ, а потім введіть значення x 10, 100, 1000 та 10000, натискаючи ENTER після кожного з них.

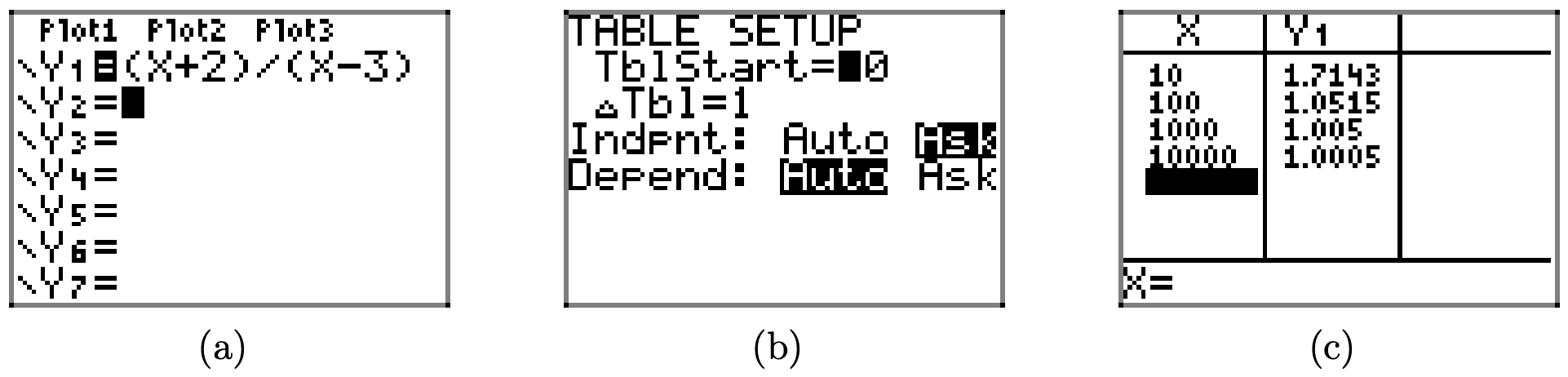
Знімок екрана 2019-07-12 в 6.20.52 PM.png — Малюнок$\PageIndex{7}$. Використання функції таблиці графічного калькулятора для дослідження кінцевої поведінки, коли x наближається до позитивної нескінченності.

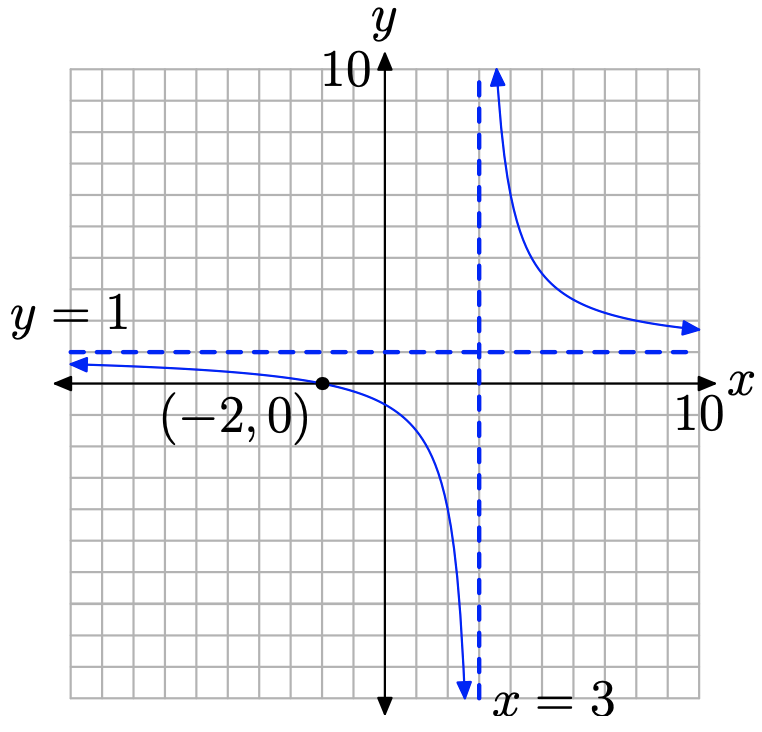
Зверніть увагу на отримані значення y у другому стовпці таблиці (стовпець Y1) на малюнку$\PageIndex{7}$ (c). Оскільки x збільшується без обмежень, значення y більші за 1, але, здається, наближаються до числа 1. Тому, коли наш графік рухається в крайнє право, він повинен наблизитися до горизонтальної асимптоти при y = 1, як показано на малюнку$\PageIndex{9}$.

Подібне зусилля прогнозує кінцеву поведінку, оскільки x зменшується без обмежень, як показано на послідовності зображень на малюнку$\PageIndex{8}$. Оскільки x зменшується без обмежень, значення y менше 1, але знову наближаються до числа 1, як показано на малюнку$\PageIndex{8}$ (c).

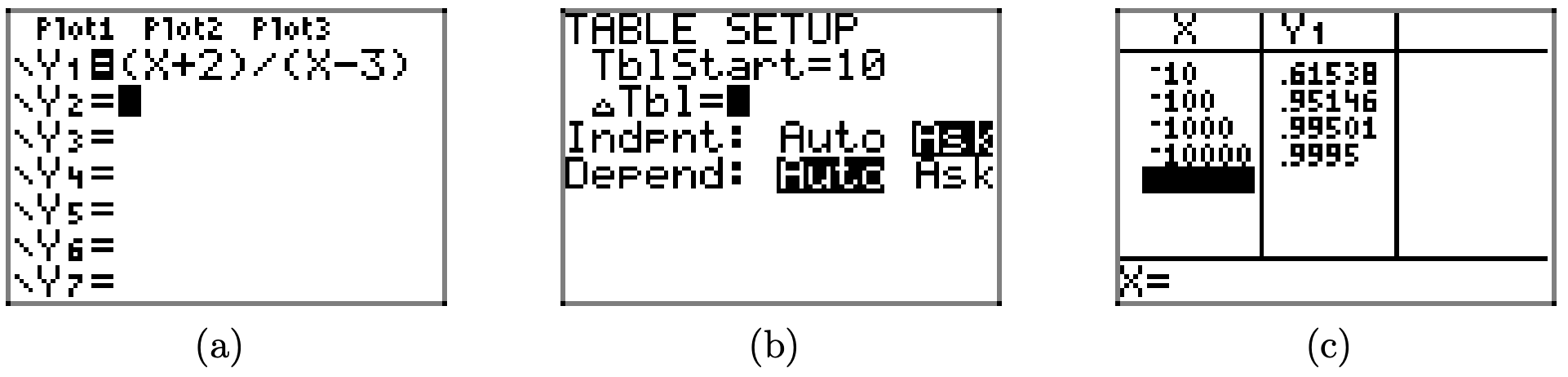
Знімок екрана 2019-07-12 о 6.22.43 PM.png — Малюнок$\PageIndex{8}$. Використання функції таблиці графічного калькулятора для дослідження кінцевої поведінки, коли x наближається до негативної нескінченності.

Докази на малюнку$\PageIndex{8}$ (c) вказують на те, що коли наш графік рухається вліво, він повинен наближатися до горизонтальної асимптоти при y = 1, як показано на малюнку$\PageIndex{9}$.

Знімок екрана 2019-07-12 в 6.26.51 PM.png — Малюнок$\PageIndex{9}$. Графік наближається до горизонтальної асимптоти y = 1 на крайньому правому і лівому кінцях.

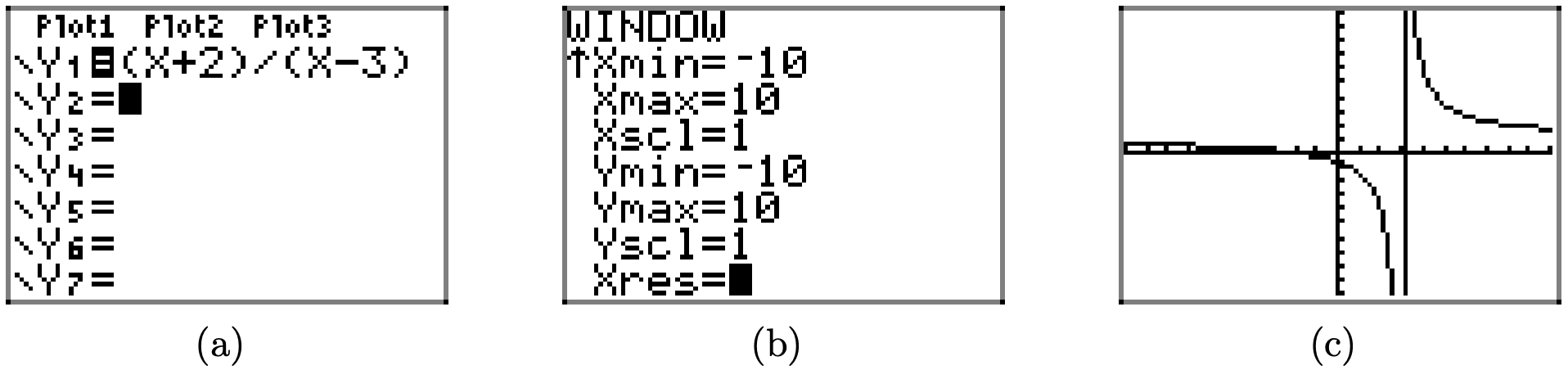
Яку роботу буде робити графічний калькулятор з графіком цієї раціональної функції? На малюнку$\PageIndex{10}$ (a) ми вводимо функцію, налаштовуємо параметри вікна, як показано на малюнку$\PageIndex{10}$ (b), потім натискаємо кнопку GRAPH, щоб отримати результат на малюнку$\PageIndex{10}$ (c).

Знімок екрана 2019-07-12 о 6.28.21 PM.png — Малюнок$\PageIndex{10}$. Креслення графіка раціональної функції за допомогою графічного калькулятора.

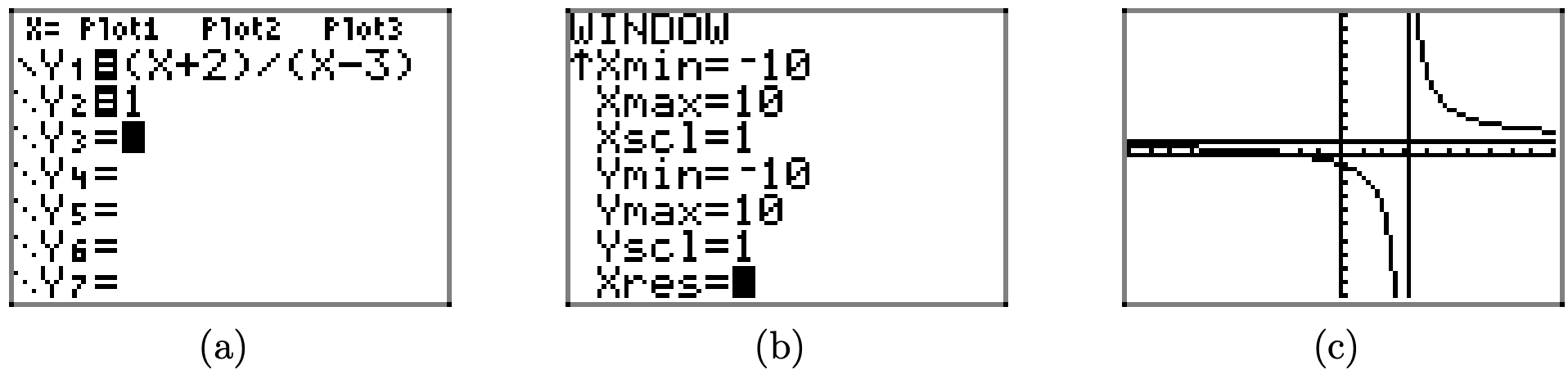
Як обговорювалося в першому розділі, графічний калькулятор надзвичайно добре управляє графіками «безперервних» функцій, але має труднощі з малюванням графіків з розривами. У разі присутньої раціональної функції графік «скакує» з негативної

нескінченність до позитивної нескінченності через вертикальну асимптоту x = 3. Калькулятор знає тільки одне: намітити точку, потім з'єднати її з раніше нанесеною точкою відрізком лінії. Отже, він робить те, що сказано, і «з'єднує» нескінченності, коли цього не повинно.

Однак, якщо ми підготувалися заздалегідь, визначаючи нулі та вертикальні асимптоти, то ми можемо інтерпретувати те, що ми бачимо на екрані на малюнку$\PageIndex{10}$ (c), і використовувати цю інформацію для отримання правильного графіка, показаного на малюнку$\PageIndex{9}$. Ми навіть можемо додати горизонтальну асимптоту до нашого графіка, як показано в послідовності на малюнку$\PageIndex{11}$.

Знімок екрана 2019-07-12 о 6.31.51 PM.png — Малюнок$\PageIndex{11}$. Додавання підозри на горизонтальну асимптоту.

Це відповідний момент для паузи та підсумовування кроків, необхідних для малювання графіка раціональної функції.

Порядок побудови графіків раціональних функцій

Розглянемо раціональну функцію\[f(x)=\frac{a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n}}{b_{0}+b_{1} x+b_{2} x^{2}+\cdots+b_{m} x^{m}}\]. Щоб намалювати графік цієї раціональної функції, дійте наступним чином:

Множник чисельника і знаменника раціональної функції f.
Визначте область раціональної функції f, перерахувавши кожне обмеження, значення незалежної змінної (зазвичай x), які роблять знаменник рівним нулю.
Визначте значення незалежної змінної, які роблять чисельник f рівним нулю і не є обмеженнями. Це нулі f і вони забезпечують х-координати х-перехоплень графа раціональної функції. Покладіть ці перехоплення на систему координат і позначте їх координатами.
Скасувати загальні фактори, щоб зменшити раціональну функцію до найнижчих. - Обмеження f, які залишаються обмеженнями цієї зменшеної форми, розмістять вертикальні асимптоти на графіку f. Намалюйте вертикальні асимптоти у вашій системі координат у вигляді пунктирних ліній і позначте їх рівняннями. - The обмеження f, які не є обмеженнями зменшеної форми, розмістять «дірки» у графі f, ми розберемося з дірками в кроці 8 цієї процедури.
Щоб визначити поведінку біля кожної вертикальної асимптоти, обчислити і побудувати по одній точці з кожного боку кожної вертикальної асимптоти.
Щоб визначити кінцеву поведінку даної раціональної функції, скористайтеся табличною здатністю вашого калькулятора, щоб визначити межу функції, коли x наближається до позитивної та/або негативної нескінченності (як ми це робили в послідовностях, показаних на малюнку$\PageIndex{7}$ та малюнку$\PageIndex{8}$). Це визначає горизонтальну асимптоту. Намалюйте горизонтальну асимптоту як пунктирну лінію на вашій системі координат і позначте її рівнянням.
Намалюйте графік раціональної функції.
Якщо ви визначили, що обмеження є «діркою», використовуйте обмеження і зменшену форму раціональної функції, щоб визначити значення y «дірки». Намалюйте відкрите коло в цьому положенні, щоб зобразити «отвір» і позначте «отвір» його координатами.
Нарешті, скористайтеся калькулятором, щоб перевірити достовірність вашого результату.

Давайте розглянемо інший приклад.

Приклад$\PageIndex{6}$

Намалюйте графік раціональної функції\[f(x)=\frac{x-2}{x^{2}-3 x-4}\]

Рішення

Ми будемо слідувати плану, представленому в Порядку графування раціональних функцій.

Крок 1: По-перше, множник як чисельник, так і знаменник.

\[f(x)=\frac{x-2}{(x+1)(x-4)}\]

Крок 2: Таким чином, f має два обмеження: x = −1 і x = 4. Тобто домен f є$D_{f}=\{s : x \neq-1,4\}$.

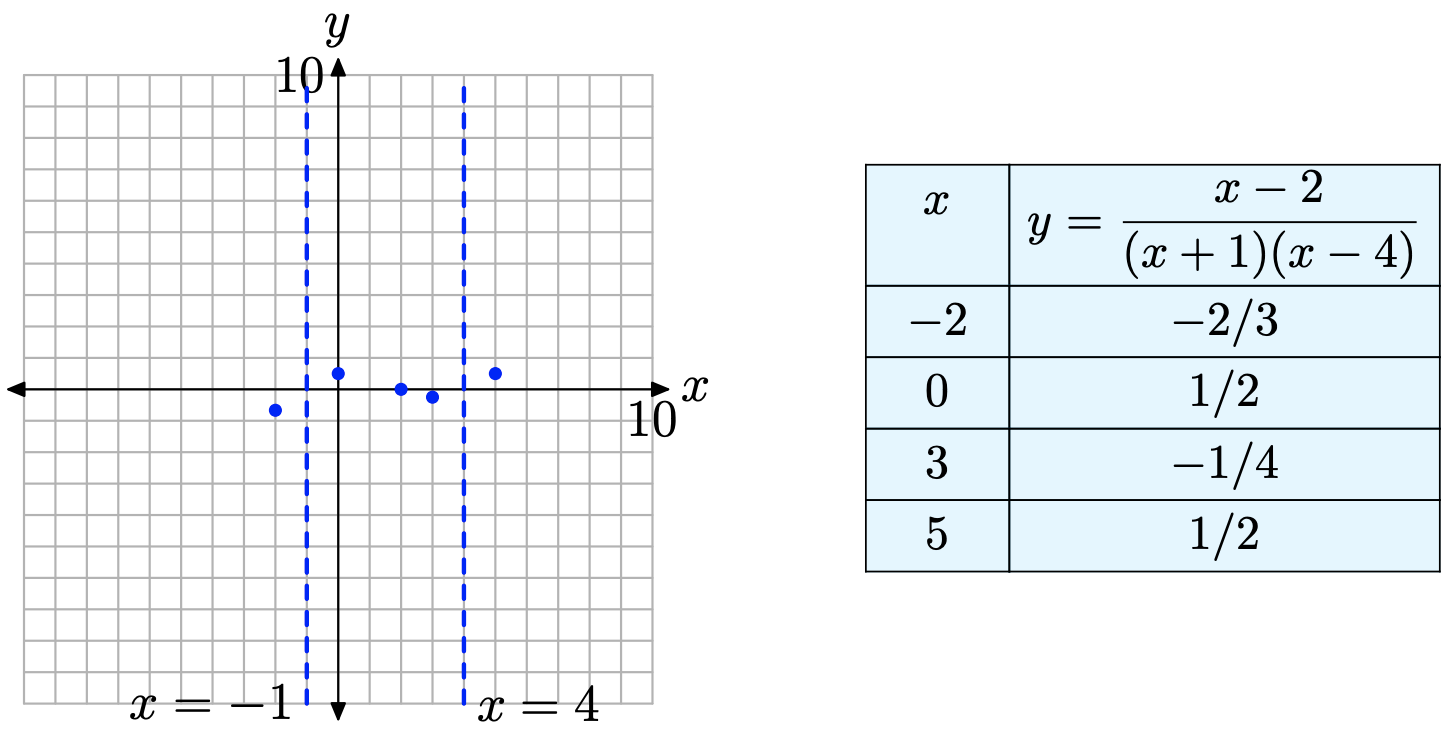
Крок 3: Чисельник рівняння (12) дорівнює нулю при x = 2, і це значення не є обмеженням. Таким чином, 2 - це нуль f і (2, 0) - це x-перехоплення графа f, як показано на малюнку$\PageIndex{12}$.

Крок 4: Зауважте, що раціональна функція вже зведена до найнижчих термінів (якби цього не було, ми б зменшили на цьому етапі). Зауважте, що обмеження x = −1 та x = 4 все ще є обмеженнями зменшеної форми. Звідси це місця і рівняння вертикальних асимптотів, які також показані на малюнку$\PageIndex{12}$.

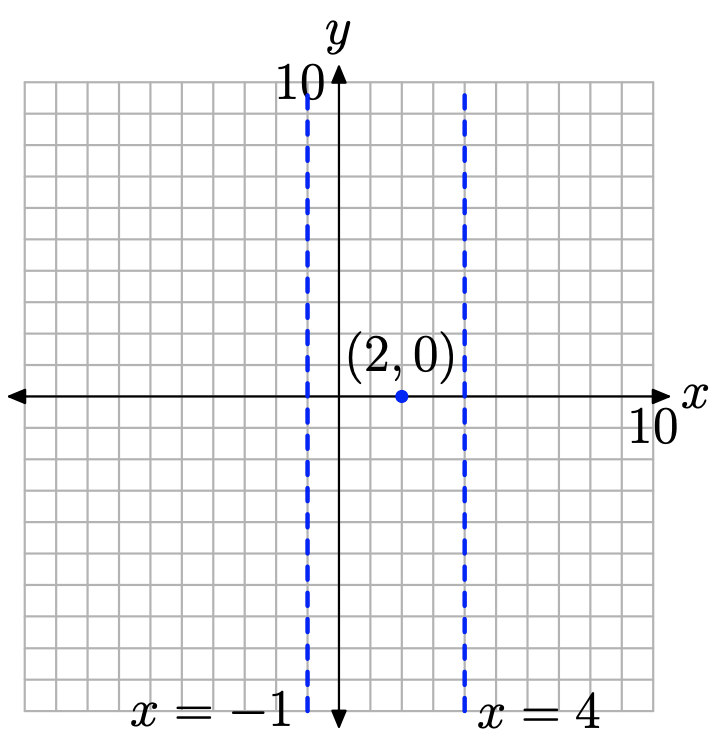
Знімок екрана 2019-07-12 в 6.41.03 PM.png — Малюнок$\PageIndex{12}$. Побудуйте Х-перехоплення і намалюйте вертикальні асимптоти.

Всі обмеження вихідної функції залишаються обмеженнями зменшеної форми. Тому ніяких «дірок» в графіку f не буде.

Крок 5: Графік вказує безпосередньо праворуч і ліворуч від кожної асимптоти, як показано на малюнку$\PageIndex{13}$. Ці додаткові точки повністю визначають поведінку графіка біля кожної вертикальної асимптоти. Наприклад, розглянемо точку (5, 1/2) безпосередньо праворуч від вертикальної асимптоти х = 4 на рис$\PageIndex{13}$. Оскільки між x = 4 і x = 5 немає перехоплення x, а графік вже знаходиться над віссю x в точці (5, 1/2), графік змушений збільшуватися до позитивної нескінченності, коли він наближається до вертикальної асимптоти x = 4. Подібні коментарі є для того, щоб поведінка з кожного боку кожної вертикальної асимптоти.

Крок 6: Використовуйте таблицю утиліту на калькуляторі, щоб визначити кінцеву поведінку раціональної функції, оскільки x зменшується та/або збільшується без обмежень. Щоб визначити кінцеву поведінку, коли x переходить до нескінченності (збільшується без обмежень), введіть рівняння у вашому калькуляторі, як показано на малюнку$\PageIndex{14}$ (а). Виберіть 2-й TBLSET і виділіть ASK для незалежної змінної. Виберіть 2-у ТАБЛИЦЮ, а потім введіть 10, 100, 1000 та 10000, як показано на малюнку$\PageIndex{14}$ (c).

Знімок екрана 2019-07-12 в 6.45.21 PM.png — Малюнок$\PageIndex{13}$. Додаткові точки допомагають визначити поведінку поблизу вертикальної асимптоти.

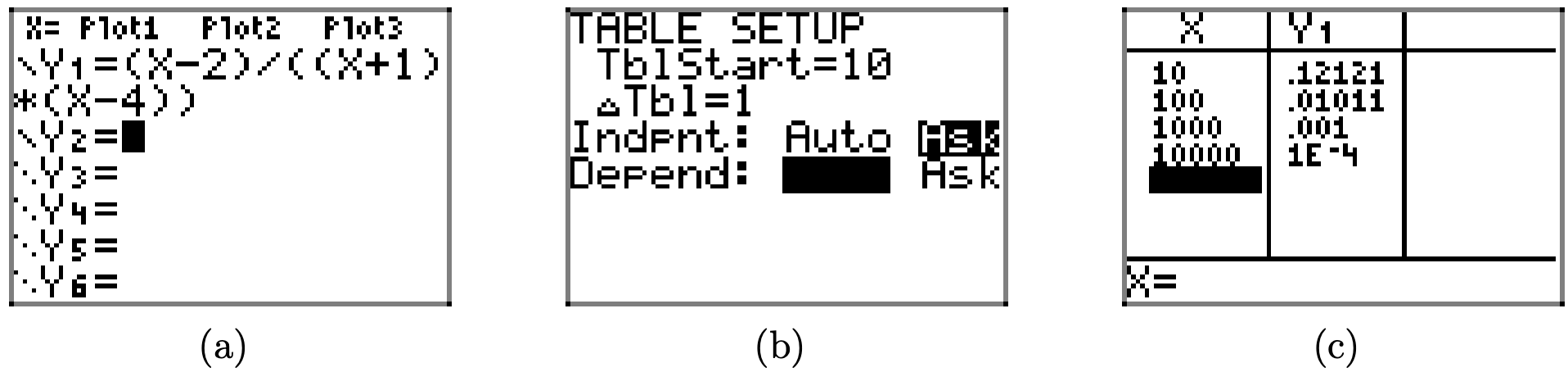
Знімок екрана 2019-07-12 в 6.46.30 PM.png — Малюнок$\PageIndex{14}$. Вивчення кінцевої поведінки, коли х наближається до позитивної

Якщо ви вивчите значення y на малюнку$\PageIndex{14}$ (c), ви побачите, що вони рухаються до нуля (1e-4 означає$1 \times 10^{-4}$, що дорівнює 0,0001). Це означає, що лінія y = 0 (вісь x) діє як горизонтальна асимптота.

Ви також можете визначити кінцеву поведінку, коли x наближається до негативної нескінченності (зменшується без обмежень), як показано на малюнку$\PageIndex{15}$. Результат на малюнку$\PageIndex{15}$ (c) дає чіткі докази того, що значення y наближаються до нуля, оскільки x переходить до негативної нескінченності. Знову ж таки, це робить y = 0 горизонтальною асимптотою.

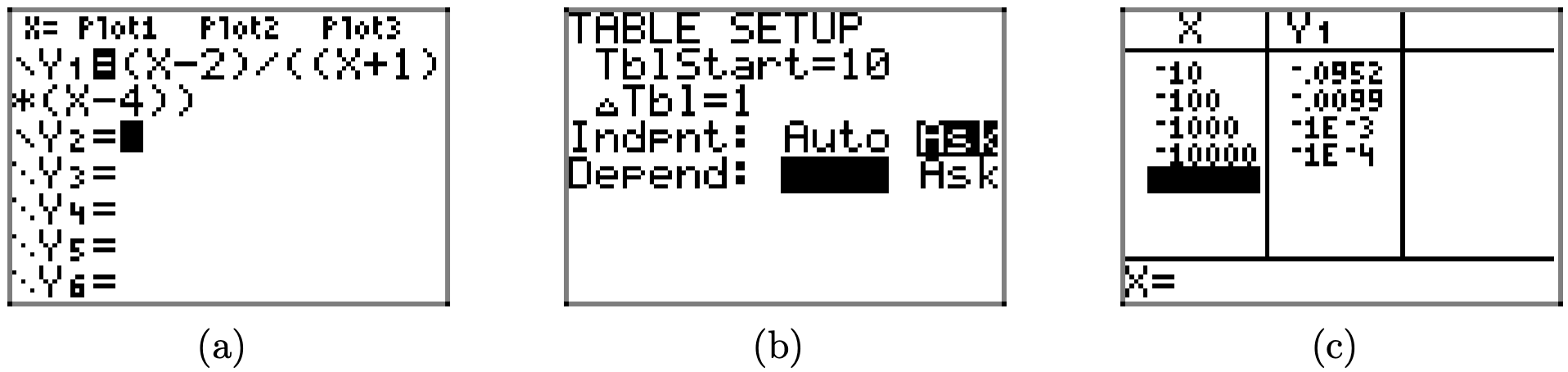
Знімок екрана 2019-07-12 в 6.49.33 PM.png — Малюнок$\PageIndex{15}$. Вивчення кінцевої поведінки, коли х наближається до негативної

Додайте горизонтальну асимптоту y = 0 до зображення на малюнку$\PageIndex{13}$.

Крок 7: Ми можемо використовувати всю зібрану на сьогоднішній день інформацію, щоб намалювати зображення, показане на малюнку$\PageIndex{16}$.

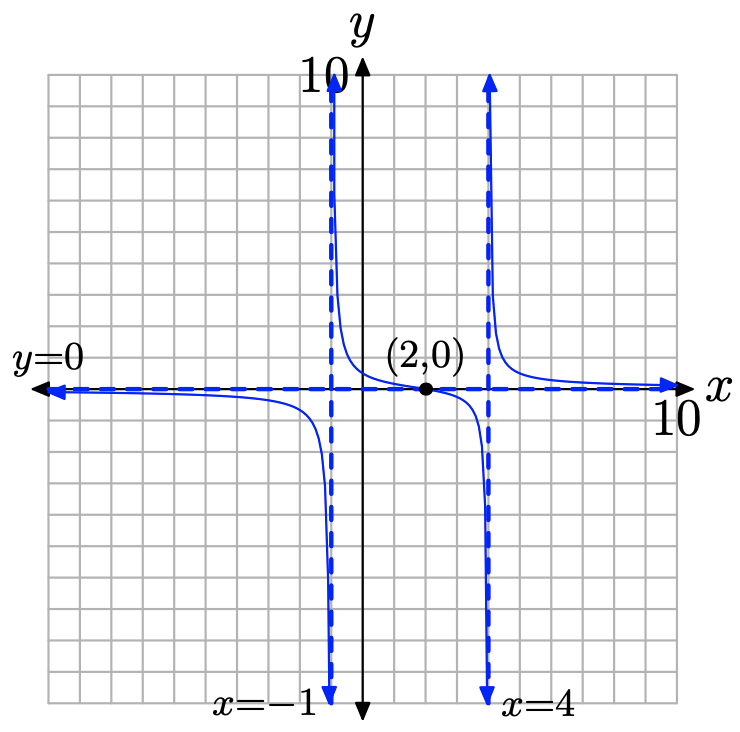
Знімок екрана 2019-07-12 в 6.51.23 PM.png — Малюнок$\PageIndex{16}$. Завершений графік біжить проти вертикальних і горизонтальних асимптотів і перетинає вісь x на нулі функції.

Крок 8: Як зазначено вище, на графіку f немає «дірок».

Крок 9: Використовуйте графічний калькулятор, щоб перевірити достовірність результату. Зверніть увагу, як графічний калькулятор обробляє графік цієї раціональної функції у послідовності на малюнку$\PageIndex{17}$. Зображення на малюнку$\PageIndex{17}$ (c) ніде не близьке до якості зображення, яке ми маємо на малюнку$\PageIndex{16}$, але там достатньо для інтуїції фактичного графіка, якщо ви підготуєтесь належним чином заздалегідь (нулі, вертикальні асимптоти, аналіз кінцевої поведінки тощо).

Знімок екрана 2019-07-12 в 6.53.25 PM.png — Малюнок$\PageIndex{17}$. Користувач графічного калькулятора повинен розшифрувати зображення на екрані перегляду калькулятора.

Вправа

Для раціональних функцій Вправи 1 - 20 дотримуйтесь Порядку побудови графіків раціональних функцій в розповіді, виконуючи кожне з наступних завдань.

Налаштуйте систему координат на графічному папері. Позначте та масштабуйте кожну вісь. Не забудьте намалювати всі лінії лінійкою.
Виконайте кожен з дев'яти кроків, перелічених у Порядку побудови раціональних функцій в розповіді.

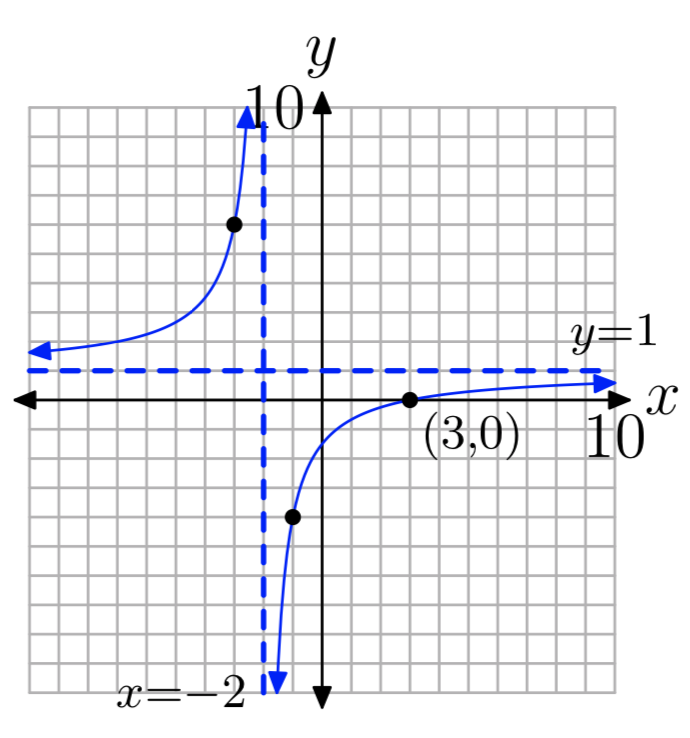
Вправа$\PageIndex{1}$

$f(x) = \frac{x−3}{x+2}$

Відповідь: $Знімок екрана 2019-08-19 в 1.33.18 PM.png$

Вправа$\PageIndex{2}$

$f(x) = \frac{x+2}{x−4}$

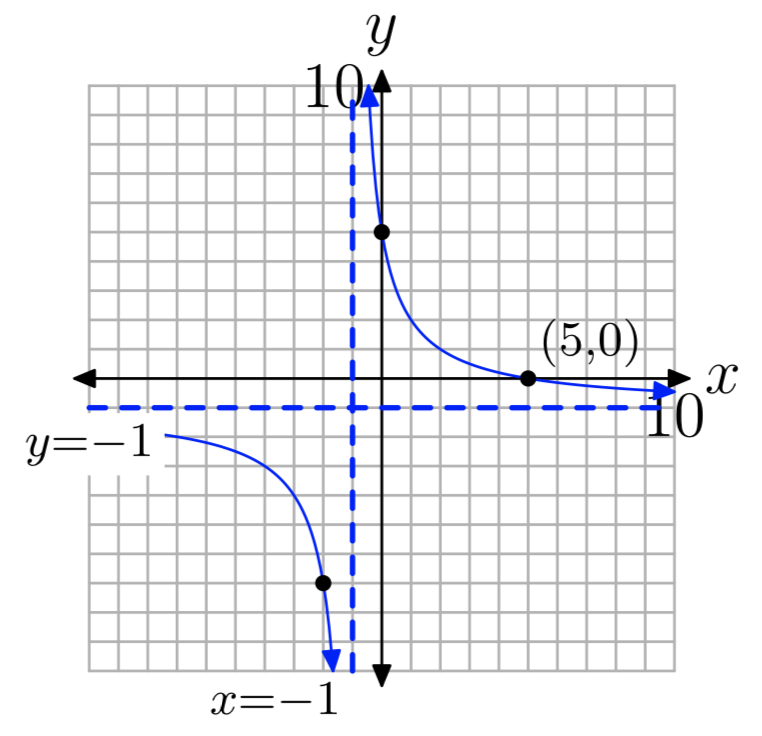
Вправа$\PageIndex{3}$

$f(x) = \frac{5−x}{x+1}$

Відповідь: $Знімок екрана 2019-08-19 в 1.33.56 PM.png$

Вправа$\PageIndex{4}$

$f(x) = \frac{x+2}{4−x}$

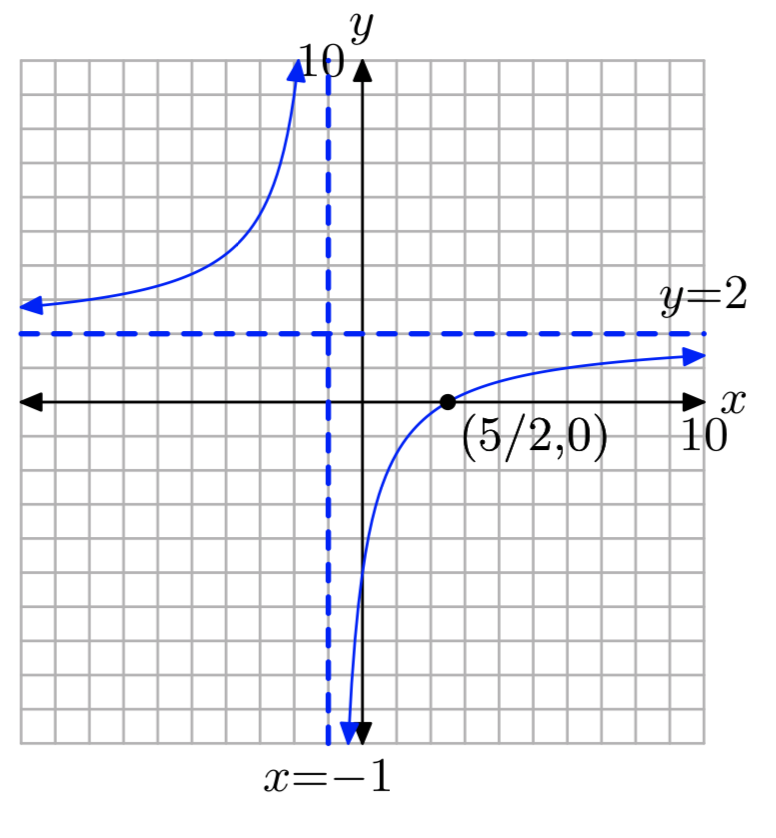
Вправа$\PageIndex{5}$

$f(x) = \frac{2x−5}{x+1}$

Відповідь: $Знімок екрана 2019-08-19 в 1.34.34 PM.png$

Вправа$\PageIndex{6}$

$f(x) = \frac{2x+5}{3−x}$

Вправа$\PageIndex{7}$

$f(x) = \frac{x+2}{x^2−2x−3}$

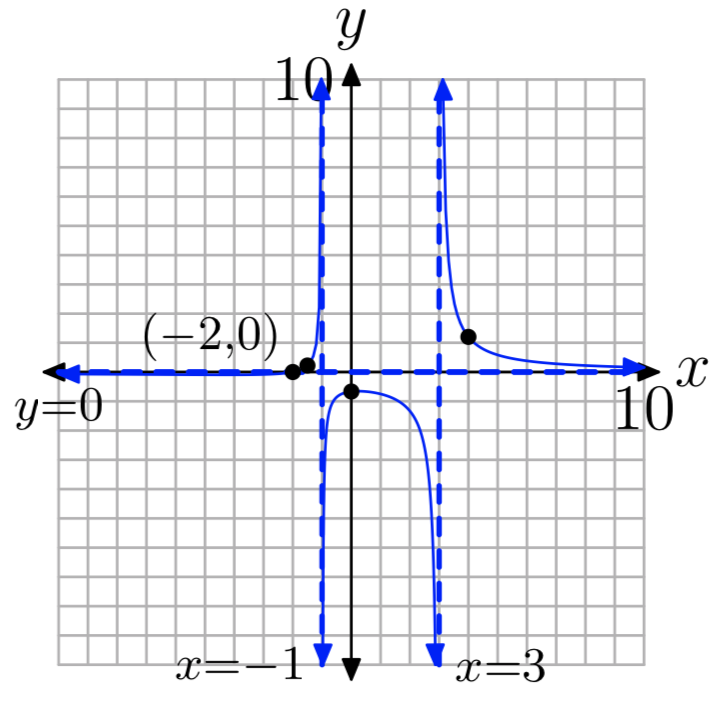
Відповідь: $Знімок екрана 2019-08-19 в 1.35.13 PM.png$

Вправа$\PageIndex{8}$

$f(x) = \frac{x−3}{x^2−3x−4}$

Вправа$\PageIndex{9}$

$f(x) = \frac{x+1}{x^2+x−2}$

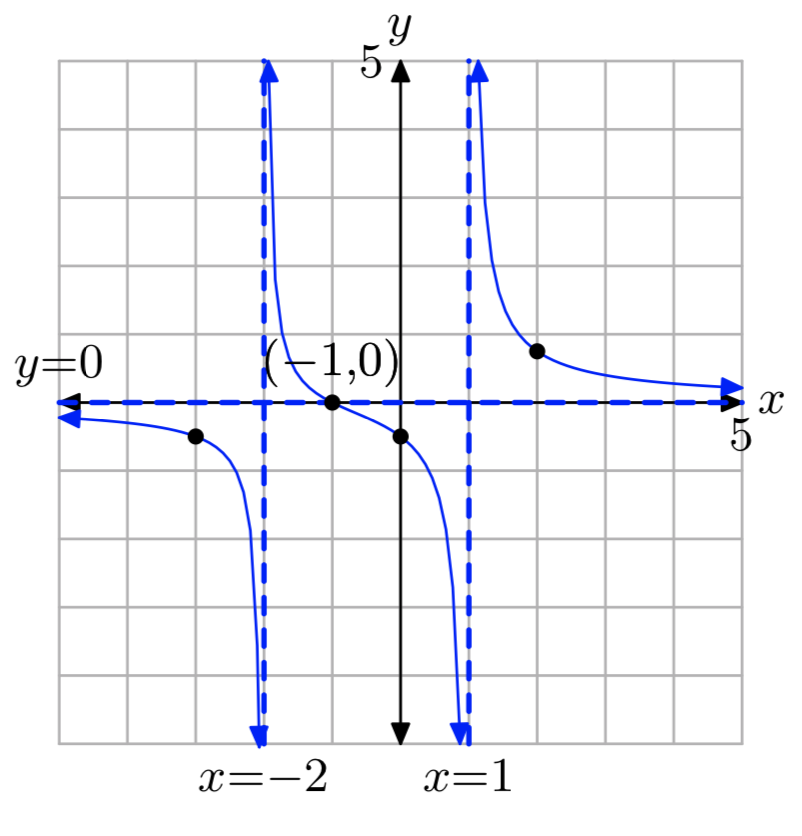
Відповідь: $Знімок екрана 2019-08-19 в 1.36.13 PM.png$

Вправа$\PageIndex{10}$

$f(x) = \frac{x−1}{x^2−x−2}$

Вправа$\PageIndex{11}$

$f(x) = \frac{x^2−2x}{x^2+x−2}$

Відповідь

Вправа$\PageIndex{12}$

$f(x) = \frac{x^2−2x}{x^2−2x−8}$

Вправа$\PageIndex{13}$

$f(x) = \frac{2x^2−2x−4}{x^2−x−12}$

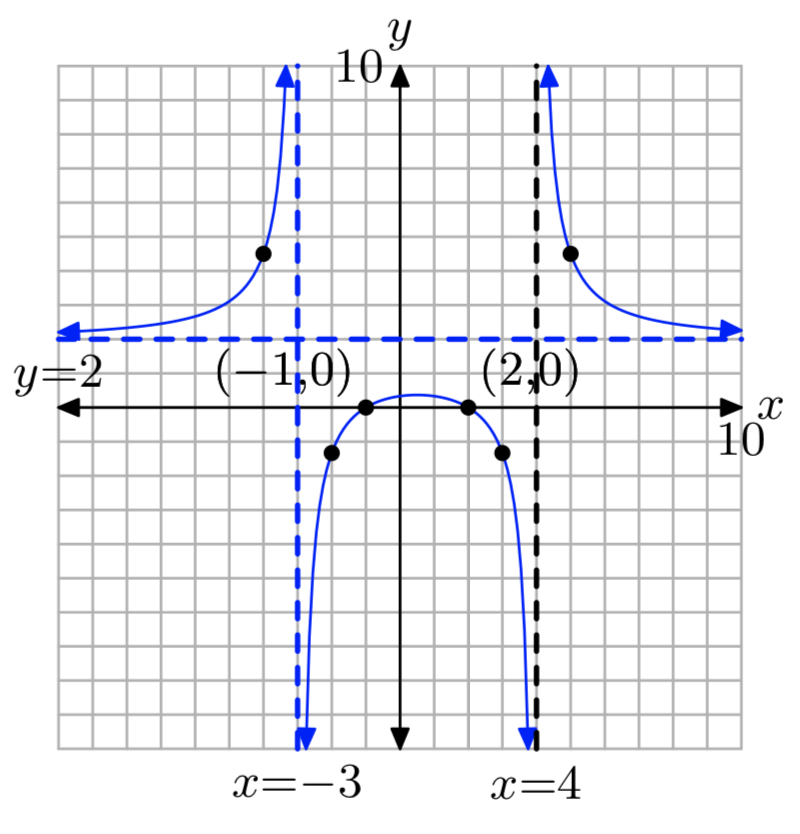
Відповідь: $Знімок екрана 2019-08-19 в 1.37.24 PM.png$

Вправа$\PageIndex{14}$

$f(x) = \frac{8x−2x^2}{x^2−x−6}$

Вправа$\PageIndex{15}$

$f(x) = \frac{x−3}{x^2−5x+6}$

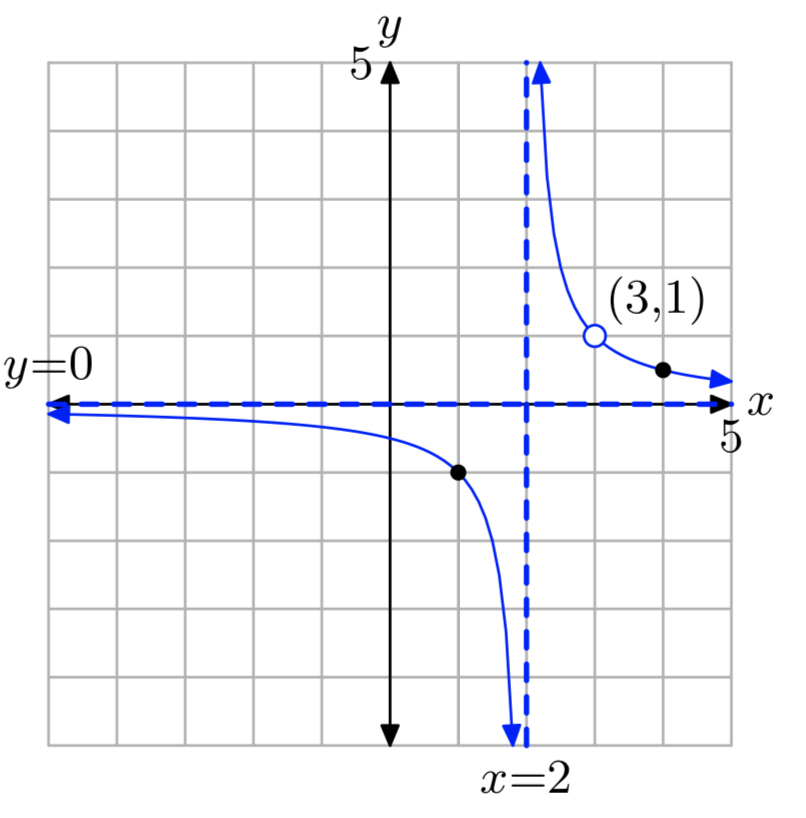
Відповідь: $Знімок екрана 2019-08-19 в 1.38.01 PM.png$

Вправа$\PageIndex{16}$

$f(x) = \frac{2x−4}{x^2−x−2}$

Вправа$\PageIndex{17}$

$f(x) = \frac{2x^2−x−6}{x^2−2x}$

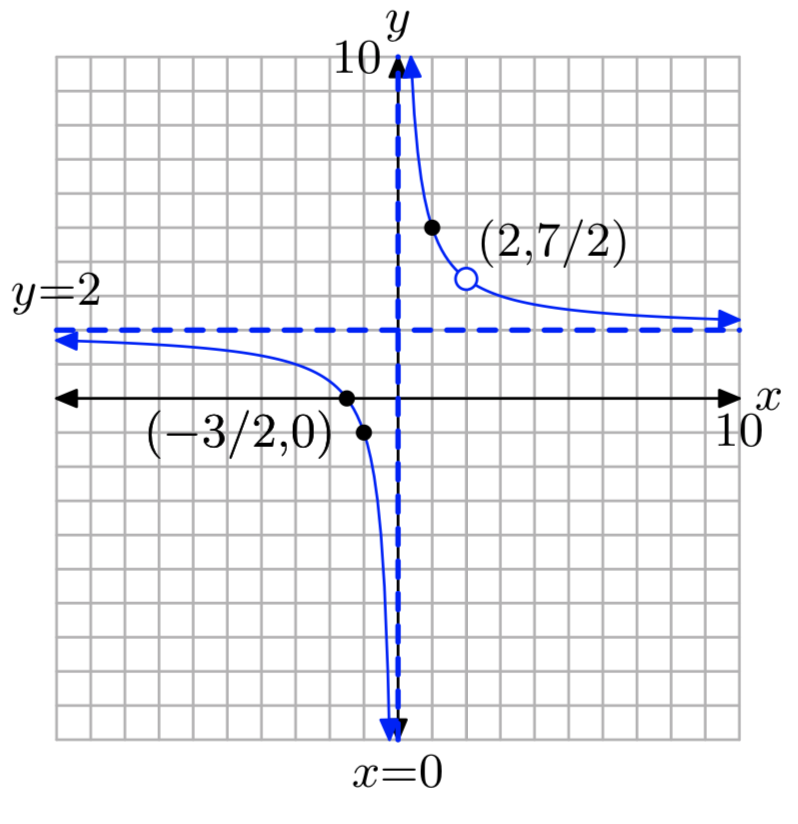
Відповідь: $Знімок екрана 2019-08-19 в 1.38.37 PM.png$

Вправа$\PageIndex{18}$

$f(x) = \frac{2x^2−x−6}{x^2−2x}$

Вправа$\PageIndex{19}$

$f(x) = \frac{4+2x−2x^2}{x^2+4x+3}$

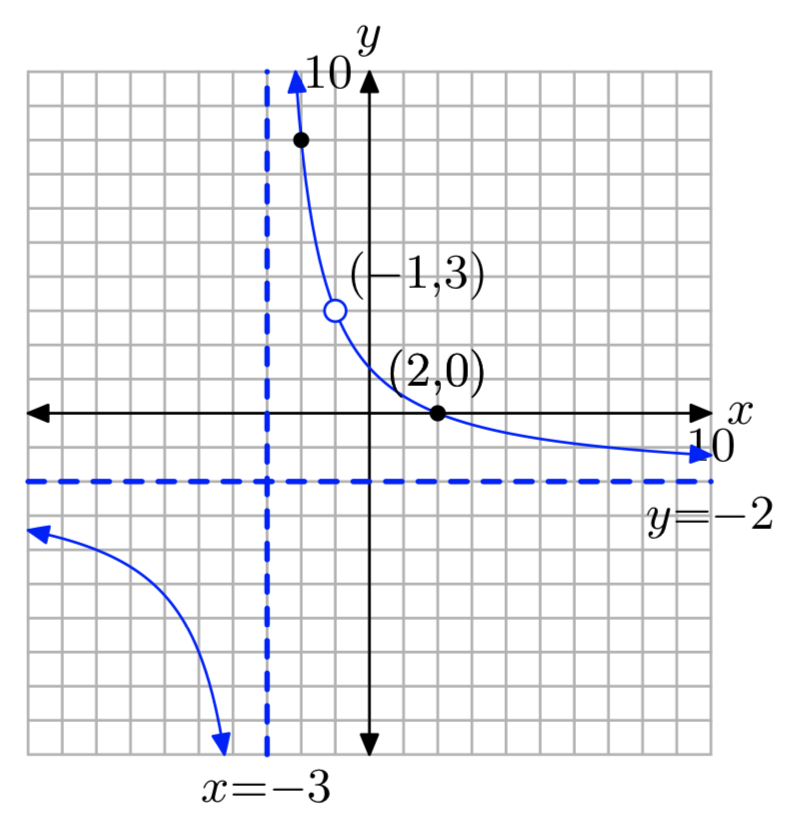
Відповідь: $Знімок екрана 2019-08-19 в 1.39.15 PM.png$

Вправа$\PageIndex{20}$

$f(x) = \frac{3x^2−6x−9}{1−x^2}$

У Вправах 21 - 28 знайти координати x-перехоплення (ів) графіка заданої раціональної функції.

Вправа$\PageIndex{21}$

$f(x) = \frac{81−x^2}{x^2+10x+9}$

Відповідь: (9, 0)

Вправа$\PageIndex{22}$

$f(x) = \frac{x−x^2}{x^2+5x−6}$

Вправа$\PageIndex{23}$

$f(x) = \frac{x^2−x−12}{x^2+2x−3}$

Відповідь: (4, 0)

Вправа$\PageIndex{24}$

$f(x) = \frac{x^2−81}{x^2−4x−45}$

Вправа$\PageIndex{25}$

$f(x) = \frac{6x−18}{x^2−7x+12}$

Відповідь: немає x-перехоплює

Вправа$\PageIndex{26}$

$f(x) = \frac{4x+36}{x^2+15x+54}$

Вправа$\PageIndex{27}$

$f(x) = \frac{x^2−9x+14}{x^2−2x}$

Відповідь: (7, 0)

Вправа$\PageIndex{28}$

$f(x) = \frac{x^2−5x−36}{x^2−9x+20}$

У вправах 29 - 36 знайдіть рівняння всіх вертикальних асимптотів.

Вправа$\PageIndex{29}$

$f(x) = \frac{x^2−7x}{x^2−2x}$

Відповідь: х = 2

Вправа$\PageIndex{30}$

$f(x) = \frac{x^2+4x−45}{3x+27}$

Вправа$\PageIndex{31}$

$f(x) = \frac{x^2−6x+8}{x^2−16}$

Відповідь: х = −4

Вправа$\PageIndex{32}$

$f(x) = \frac{x^2−11x+18}{2x−x^2}$

Вправа$\PageIndex{33}$

$f(x) = \frac{x^2+x−12}{−4x+12}$

Відповідь: немає вертикальних асимптотів

Вправа$\PageIndex{34}$

$f(x) = \frac{x^2−3x−54}{9x−x^2}$

Вправа$\PageIndex{35}$

$f(x) = \frac{16−x^2}{x^2+7x+12}$

Відповідь: x = −3

Вправа$\PageIndex{36}$

$f(x) = \frac{x^2−11x+30}{−8x+48}$

У Вправи 37 - 42 використовуйте графічний калькулятор для визначення поведінки заданої раціональної функції, оскільки x наближається як до позитивної, так і до негативної нескінченності, виконуючи наступні завдання:

Завантажте раціональну функцію в Y=меню вашого калькулятора.
Скористайтеся функцією ТАБЛИЦЯ вашого калькулятора, щоб визначити значення f (x) для x = 10, 100, 1000 та 10000. Запишіть ці результати на домашнє завдання в табличній формі.
Скористайтеся функцією ТАБЛИЦЯ вашого калькулятора, щоб визначити значення f (x) для x = −10, −100, −1000 та −10000. Запишіть ці результати на домашній роботі в табличній формі.
Використовуйте результати табличного дослідження, щоб визначити рівняння горизонтальної асимптоти.

Вправа$\PageIndex{37}$

$f(x) = \frac{2x+3}{x−8}$

Відповідь

Горизонтальна асимптота при y = 2.

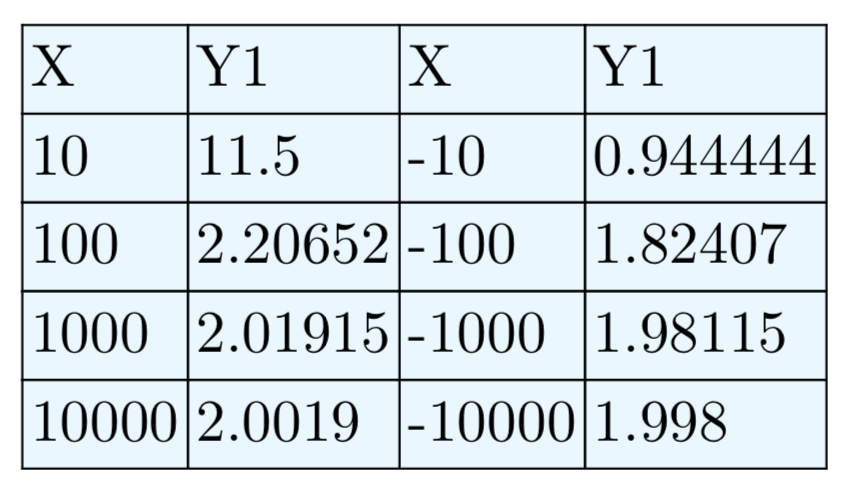
$Знімок екрана 2019-08-19 в 1.41.33 PM.png$

Вправа$\PageIndex{38}$

$f(x) = \frac{4−3x}{x+2}$

Вправа$\PageIndex{39}$

$f(x) = \frac{4−x^2}{x^2+4x+3}$

Відповідь

Горизонтальна асимптота при y = −1.

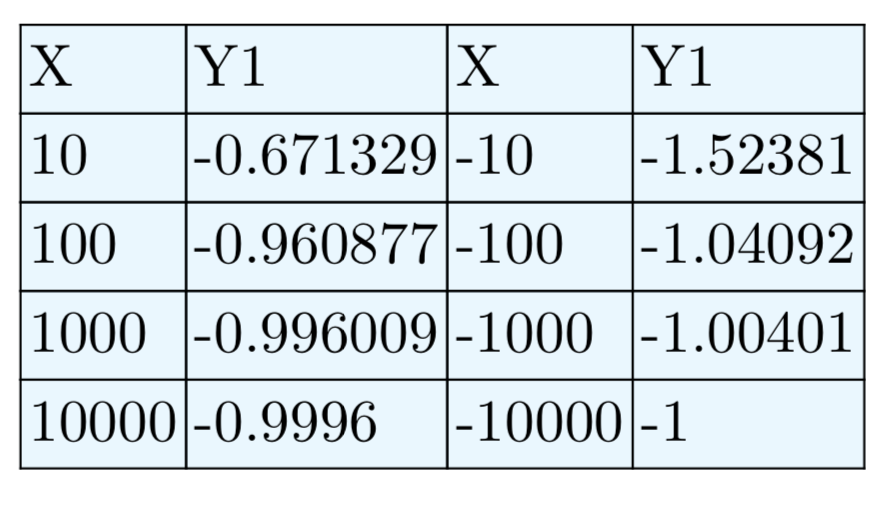
$Знімок екрана 2019-08-19 в 1.42.24 PM.png$

Вправа$\PageIndex{40}$

$f(x) = \frac{10−2x^2}{x^2−4}$

Вправа$\PageIndex{41}$

$f(x) = \frac{x^2−2x−3}{2x^2−3x−2}$

Відповідь

Горизонтальна асимптота в$y = \frac{1}{2}$.

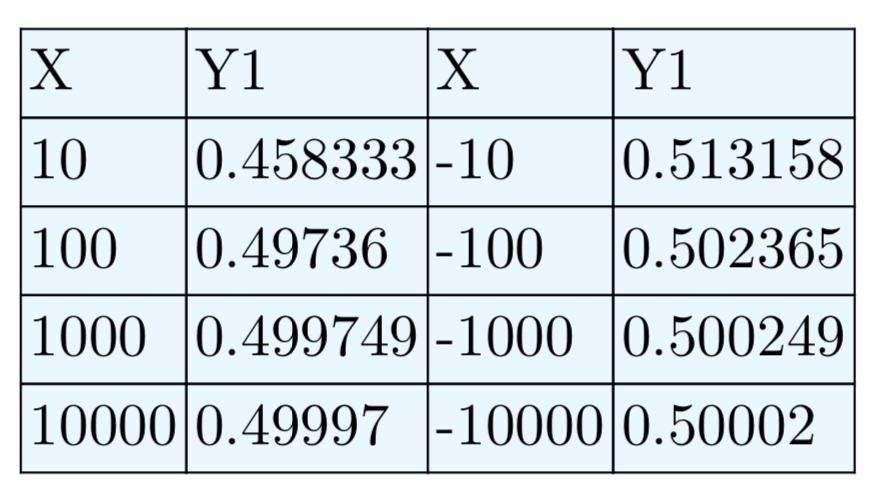
$Знімок екрана 2019-08-19 в 1.43.20 PM.png$

Вправа$\PageIndex{42}$

$f(x) = \frac{2x^2−3x−5}{x^2−x−6}$

У вправах 43 - 48 використовують чисто аналітичний метод для визначення області заданої раціональної функції. Опишіть домен за допомогою нотації set-builder.

Вправа$\PageIndex{43}$

$f(x) = \frac{x^2−5x−6}{−9x−9}$

Відповідь: Домен = {x:$x \ne −1$}

Вправа$\PageIndex{44}$

$f(x) = \frac{x^2+4x+3}{x^2−5x−6}$

Вправа$\PageIndex{45}$

$f(x) = \frac{x^2+5x−24}{x^2−3x}$

Відповідь: Домен = {x:$x \ne 3, 0$}

Вправа$\PageIndex{46}$

$f(x) = \frac{x^2−3x−4}{x^2−5x−6}$

Вправа$\PageIndex{47}$

$f(x) = \frac{x^2−4x+3}{x−x^2}$

Відповідь: Домен = {x:$x \ne 0, 1$}

Вправа$\PageIndex{48}$

$f(x) = \frac{x^2−4}{x^2−9x+14}$