7.2: Зменшення раціональних функцій

Мета цього розділу - дізнатися, як звести раціональний вираз до «найнижчих термінів». Звичайно, це означає, що нам доведеться зрозуміти, що мається на увазі під словосполученням «найнижчі терміни». Маючи цю думку на увазі, ми починаємо з обговорення найбільшого спільного дільника пари цілих чисел.

Спочатку визначаємо, що ми маємо на увазі під «подільністю».

Визначення

Припустимо, що у нас є пара цілих чисел a і b. ми говоримо, що «a - дільник b», або «a ділить b» тоді і тільки тоді, коли є інше ціле число k так, що b = ak. Інший спосіб сказати те ж саме - сказати, що a ділить b, якщо при діленні b на a залишок дорівнює нулю.

Давайте розглянемо приклад.

Приклад$\PageIndex{1}$

Які дільники 12?

Рішення

$12=1 \times 12$Тому що і 1, і 12 є дільниками 12. $12=2 \times 6$Тому що і 2, і 6 є дільниками 12. Нарешті$12=3 \times 4$, тому що обидва 3 і 4 є дільниками 12. Якщо ми перерахуємо їх у порядку зростання, дільники 12 $$1,2,3,4,6, \text { and } 12$$

Давайте розглянемо інший приклад.

Приклад$\PageIndex{2}$

Які дільники 18?

Рішення

$18=1 \times 18$Тому що і 1, і 18 є дільниками 18. Аналогічно$18=3 \times 6$,$18=2 \times 9$ і, так в порядку зростання, дільники 18 є

$$1,2,3,6,9, \text { and } 18$$

Найбільший спільний дільник двох або більше цілих чисел є найбільшим дільником, який поділяють цілі числа в загальному. Приклад повинен зробити це зрозумілим.

Приклад$\PageIndex{3}$

Який найбільший спільний дільник 12 і 18?

Рішення

У прикладі 2 та прикладі 3 ми побачили наступне.

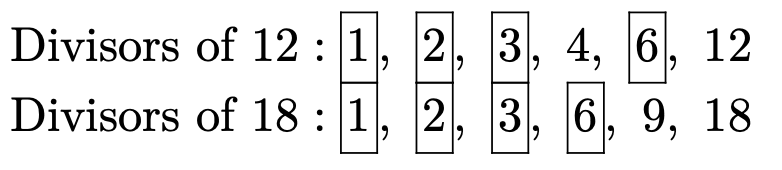
Ми обрамляли дільники, які 12 і 18 мають спільне. Вони бувають 1, 2, 3 і 6. «Найбільший» з цих «загальних» дільників - 6. Отже, ми говоримо, що «найбільший спільний дільник 12 і 18 - це 6».

Визначення

Найбільший спільний дільник двох цілих чисел a та b є найбільшим спільним дільником. Ми будемо використовувати позначення $$GCD(a, b)$$ для представлення найбільшого спільного дільника a і b.

Таким чином, як ми бачили в прикладі 4, НСД (12, 18) = 6.

Коли найбільший спільний дільник пари цілих чисел є одним, ми даємо цій парі спеціальне ім'я.

Визначення

Нехай a і b будуть цілими числами. Якщо найбільший спільний дільник a і b дорівнює одиниці, тобто якщо НСД (a, b) = 1, то скажемо, що a і b відносно прості.

Наприклад:

• 9 і 12 не є відносно простими, оскільки НСД (9, 12) = 3.
• 10 і 15 не є відносно простими, оскільки НСД (10, 15) = 5.
• 8 і 21 є відносно простими, оскільки НСД (8, 21) = 1.

Тепер ми можемо визначити, що мається на увазі, коли ми говоримо, що раціональне число зводиться до найнижчих.

Визначення

Раціональне число у вигляді p/q, де p і q є цілими числами, як кажуть, зменшується до найнижчих членів якщо і тільки тоді, коли НСД (p, q) = 1. Тобто p/q зводиться до найнижчих, якщо найбільший спільний дільник як чисельника, так і знаменника дорівнює 1.

Як ми бачили в прикладі$\PageIndex{3}$, найбільшим спільним дільником 12 і 18 є 6. Тому фракція 12/18 не зводиться до найнижчих показників. Однак ми можемо зменшити 12/18 до найнижчих чисел, розділивши як чисельник, так і знаменник на їх найбільший спільний дільник. Тобто,

$$\frac{12}{18}=\frac{12 \div 6}{18 \div 6}=\frac{2}{3}$$

Зверніть увагу, що НСД (2, 3) = 1, тому 2/3 зменшується до найнижчих показників.

Коли важко встановити найбільший спільний дільник, ми вважаємо, що ефективніше діяти наступним чином:

• Простий множник як чисельник, так і знаменник.

• Скасувати загальні фактори.

Таким чином, щоб зменшити 12/18 до найнижчих чисел, спочатку виражаємо як чисельник, так і знаменник як добуток простих чисел, потім скасуємо загальні прості числа.

$$\frac{12}{18}=\frac{2 \cdot 2 \cdot 3}{2 \cdot 3 \cdot 3}=\frac{\not{2} \cdot 2 \cdot \not{3}}{\not{2} \cdot 3 \cdot \not{3}}=\frac{2}{3}$$

Коли ви скасуєте 2, ви фактично ділите обидва чисельника і знаменника на 2. Коли ви скасуєте 3, ви фактично ділите обидва чисельник і знаменник на 3. Зверніть увагу, що виконання обох (ділення на 2, а потім ділення на 3) еквівалентно діленню чисельника і знаменника на 6.

Ми будемо віддавати перевагу цій останній техніці саме тому, що вона ідентична техніці, яку ми будемо використовувати для зменшення раціональних функцій до найнижчих показників. Однак ця методика «скасування» має деякі підводні камені, тому давайте знайдемо хвилинку, щоб обговорити деякі поширені помилки скасування.

Скасування

Ви можете викликати деякі досить гарячі дебати серед викладачів математики, невинно згадуючи слово «скасування». Здається, є два діаметрально протилежних табори, ті, хто не проти, коли їхні учні використовують техніку скасування, а з іншого боку - ті, які відмовляються навіть використовувати термін «скасування» у своїх заняттях.

Обидві сторони аргументу мають заслуги. Як ми показали в рівнянні (8), ми можемо зменшити 12/18 досить ефективно, просто скасувавши загальні фактори. З іншого боку, інструктори з другого табору вважають за краще використовувати фразу «фактор out a 1» замість фрази «скасувати», заохочуючи своїх учнів зменшити 12/18 наступним чином.

$$\frac{12}{18}=\frac{2 \cdot 2 \cdot 3}{2 \cdot 3 \cdot 3}=\frac{2}{3} \cdot \color{blue}{\frac{2 \cdot 3}{2 \cdot 3}}=\frac{2}{3} \cdot 1=\frac{2}{3}$$

Це цілком дійсна техніка і така, яка, чесно кажучи, дозволяє уникнути пливун «помилок скасування». Інструктори, які втомилися спостерігати за тим, як їхні учні «скасовують», коли вони не повинні, швидше за все, сприятимуть цій останній техніці.

Однак, якщо ми можемо допомогти нашим студентам уникнути «помилок скасування», ми вважаємо за краще дозволити нашим студентам скасувати загальні фактори (як ми це робили в рівнянні (8)) при скороченні дробів, таких як 12/18, до найнижчих. Отже, маючи на увазі ці думки, давайте обговоримо деякі найпоширеніші помилки скасування.

Почнемо з найважливішої поради.

Як уникнути помилок скасування

Ви можете скасувати лише фактори, а не доповнення. Щоб уникнути помилок скасування, повністю враховуйте, перш ніж почати скасувати.

Попередження

Багато з подальших розрахунків невірні. Вони є прикладами поширених помилок, які допускаються при виконанні скасування. Переконайтеся, що ви уважно читаєте і уникайте просто «сканування» цих розрахунків.

Як перший приклад розглянемо раціональне вираз

$$\frac{2+6}{2}$$

яка явно дорівнює 8/2, або 4. Однак якщо скасувати в цій ситуації, як в

$$\frac{2+6}{2}=\frac{\not{2}+6}{\not{2}}$$

ви точно не отримаєте такий же результат. Отже, що ж сталося?

Зверніть увагу, що в чисельнику рівняння (10) 2 і 6 розділені знаком плюс. Таким чином, вони не є факторами; вони є доповненнями! Вам заборонено скасовувати доповнення, лише фактори.

Припустимо, для порівняння, що раціональне вираження було

$$\frac{2 \cdot 6}{2}$$

яка явно дорівнює 12/2, або 6. У цьому випадку 2 і 6 в чисельнику розділені символом множення, тому вони є множниками і допускається скасування, як в

$$\frac{2 \cdot 6}{2}=\frac{\not{2} \cdot 6}{\not{2}}=6$$

Тепер, перш ніж відхилити ці приклади як тривіальні, розглянемо такі приклади, які ідентичні за структурою. По-перше, розглянемо

$$\frac{x+(x+2)}{x}=\frac{\not{x}+(x+2)}{\not{x}}=x+2$$

Це скасування ідентичне тому, що виконується в рівнянні (10) і не допускається. У чисельнику зверніть увагу, що x і (x+2) розділені символом додавання, тому вони є додатками. Вам заборонено скасовувати доповнення!

І навпаки, розглянемо наступний приклад.

$$\frac{x(x+2)}{x}=\frac{\not{x}(x+2)}{\not{x}}=x+2$$

У чисельнику цього прикладу x і (x+2) відокремлюються непрямим множенням. Значить, вони є факторами і скасування допустимо.

Подивіться ще раз на рівняння (10), де правильна відповідь повинна була бути 8/2, або 4. Ми помилково знайшли відповідь 6, тому що ми скасували доповнення. Обхідний шлях полягає в тому, щоб спочатку множити чисельник рівняння (10), а потім скасувати, як показано нижче.

$$\frac{2+6}{2}=\frac{2(1+3)}{2}=\frac{\not{2}(1+3)}{\not{2}}=1+3=4$$

Зауважимо, що ми скасували чинники в цьому підході, що допустимо, і отримали правильну відповідь 4.

Попередження

Ми закінчили обговорювати поширені помилки скасування, і ви не можете продовжувати читати з упевненістю, що вся математика правильно представлена.

Зменшення раціональних виразів у x

Тепер, коли ми обговорили деякі фундаментальні ідеї та методи, давайте застосуємо те, що ми навчилися, до раціональних виразів, які є функціями незалежної змінної (зазвичай x). Почнемо з простого прикладу.

Приклад$\PageIndex{4}$

Звести раціональне вираження $$\frac{2 x-6}{x^{2}-7 x+12}$$ до найнижчих термінів. Для яких значень x дійсний ваш результат?

Рішення

У чисельнику множник дорівнює 2, як у 2x − 6 = 2 (x − 3).

Знаменник - квадратичний триноміал з ac = (1) (12) = 12. Пара цілих чисел −3 та −4 має добуток 12 та суму −7, тож множники знаменника, як показано на малюнку.

$$\frac{2 x-6}{x^{2}-7 x+12}=\frac{2(x-3)}{(x-3)(x-4)}$$

Тепер, коли і чисельник, і знаменник враховуються, ми можемо скасувати загальні множники.

\[\frac{2 x-6}{x^{2}-7 x+12}=\frac{2(x-3)}{(x-3)(x-4)}=\frac{2}{x-4}\]

Таким чином, ми показали, що $$\frac{2 x-6}{x^{2}-7 x+12}=\frac{2}{x-4}$$

У рівнянні (15) ми заявляємо, що вираз зліва (вихідний вираз) ідентично виразу праворуч для всіх значень x.

Власне, є два помітних винятку, перше з яких - х = 3. Якщо підставити x = 3 в ліву частину рівняння (15), то отримаємо

$$\frac{2 x-6}{x^{2}-7 x+12}=\frac{2(3)-6}{(3)^{2}-7(3)+12}=\frac{0}{0}$$

Ми не можемо розділити на нуль, тому ліва частина рівняння (15) не визначена, якщо x = 3. Тому результат у рівнянні (15) не є дійсним, якщо x = 3.

Аналогічно, якщо ми вставимо x = 4 в лівій частині рівняння (15),

$$\frac{2 x-6}{x^{2}-7 x+12}=\frac{2(4)-6}{(4)^{2}-7(4)+12}=\frac{2}{0}$$

Знову ж таки, ділення на нуль не визначено. Ліва частина рівняння (15) не визначена, якщо x = 4, тому результат у рівнянні (15) не є дійсним, якщо x = 4. Зверніть увагу, що права частина рівняння (15) також не визначена при x = 4.

Однак алгебраїчна робота, яку ми зробили вище, гарантує, що ліва сторона рівняння (15) буде ідентична правій частині рівняння (15) для всіх інших значень x Наприклад, якщо ми підставимо x = 5 в ліву частину рівняння (15),

$$\frac{2 x-6}{x^{2}-7 x+12}=\frac{2(5)-6}{(5)^{2}-7(5)+12}=\frac{4}{2}=2$$

З іншого боку, якщо ми підставимо x = 5 в праву частину рівняння (15),

$$\frac{2}{x-4}=\frac{2}{5-4}=2$$

Отже, обидві сторони рівняння (15) однакові, коли x = 5. Аналогічним чином ми могли б перевірити достовірність ідентичності в рівнянні (15) для всіх інших значень x

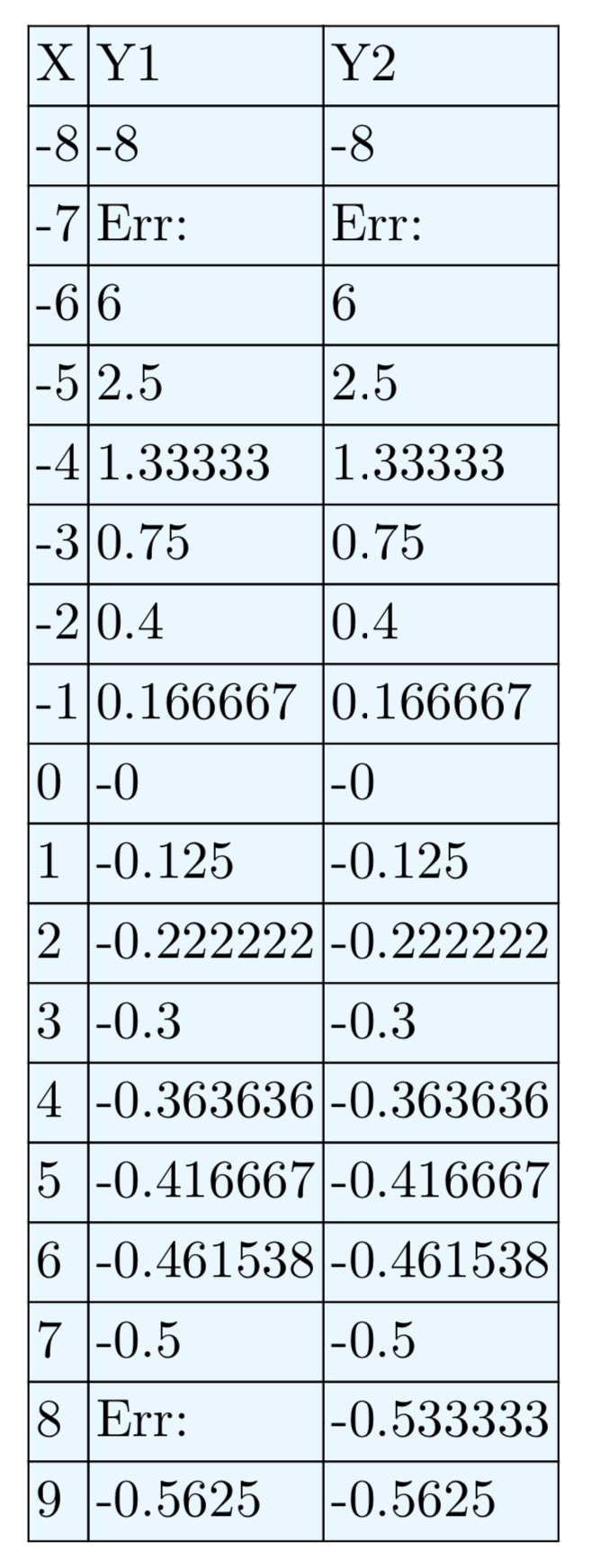
Ви можете скористатися графічним калькулятором для перевірки ідентичності в рівнянні (15). Завантажте ліву та праву сторони рівняння (15) у меню Y =, як показано на малюнку$\PageIndex{1}$ (а). Натисніть 2nd TBLSET і відрегулюйте параметри, як показано на малюнку$\PageIndex{1}$ (b). Переконайтеся, що ви виділили AUTO як для незалежних, так і для залежних змінних і натисніть ENTER на кожній, щоб зробити вибір постійним. На малюнку$\PageIndex{1}$ (b) зауважте, що ми встановили TBLStart = 0 і ΔTbl = 1. Натисніть 2nd TABLE, щоб отримати табличні результати, показані на малюнку$\PageIndex{1}$ (c).

Малюнок$\PageIndex{1}$. Використовуючи графічний калькулятор, щоб перевірити, чи ліва і права сторони рівняння (15) ідентичні.

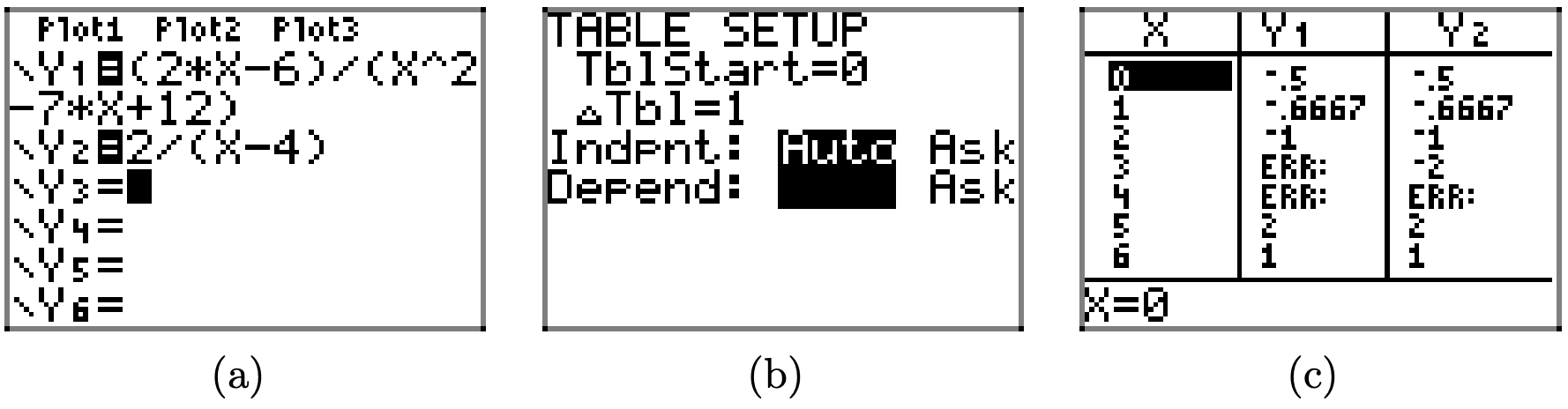
Пам'ятайте, що ми розмістили ліву та праву сторони рівняння (15) у Y1 та Y2 відповідно.

• У табличних результатах малюнка$\PageIndex{1}$ (c) зверніть увагу на повідомлення ERR (помилка) в Y1, коли x = 3 і x = 4. Це узгоджується з нашими висновками вище, де ліва частина рівняння (15) була невизначена через наявність нуля в знаменнику, коли x = 3 або x = 4.
• У табличних результатах рисунка$\PageIndex{1}$ (c) зверніть увагу, що значення Y1 і Y2 узгоджуються для всіх інших значень x.

Нас призводять до наступного ключового результату.

Обмеження

Загалом, при скороченні раціонального виразу до найнижчих членів, отриманий вираз повинен бути ідентичним вихідному виразу для всіх значень змінних в кожному виразі, зберігайте ті значення змінних, які роблять будь-який знаменник рівним нулю. Це стосується знаменника в вихідному вираженні, всіх проміжних виразів у вашій роботі, і кінцевого результату. Ми будемо посилатися на будь-які значення змінної, які роблять будь-який знаменник рівним нулю як обмеження.

Давайте розглянемо інший приклад.

Приклад$\PageIndex{5}$

Зменшіть вираз $$\frac{2 x^{2}+5 x-12}{4 x^{3}+16 x^{2}-9 x-36}$$ до найнижчих термінів. Зазначте всі обмеження.

Рішення

Чисельник є квадратичним тріноміалом з ac = (2) (−12) = −24. Пари цілих чисел −3 та 8 мають добуток −24 та суму 5. Розбийте середній член многочлена в чисельнику на суму, використовуючи цю цілу пару, потім множник шляхом групування.

$$\begin{aligned} 2 x^{2}+5 x-12 &=2 x^{2}-3 x+8 x-12 \\ &=x(2 x-3)+4(2 x-3) \\ &=(x+4)(2 x-3) \end{aligned}$$

Фактор знаменника шляхом групування.

$$\begin{aligned} 4 x^{3}+16 x^{2}-9 x-36 &=4 x^{2}(x+4)-9(x+4) \\ &=\left(4 x^{2}-9\right)(x+4) \\ &=(2 x+3)(2 x-3)(x+4) \end{aligned}$$

Зверніть увагу, як різниця двох квадратів була використана для фактора$4x^2 − 9 = (2x + 3)(2x − 3)$ на останньому кроці.

Тепер, коли ми враховували як чисельник і знаменник, ми скасуємо загальні фактори.

\[\begin{aligned} \frac{2 x^{2}+5 x-12}{4 x^{3}+16 x^{2}-9 x-36} &=\frac{(x+4)(2 x-3)}{(2 x+3)(2 x-3)(x+4)} \\ &=\frac{(x+4)(2 x-3)}{(2 x+3)(2 x-3)(x+4)} \\ &=\frac{1}{2 x+3} \end{aligned}\]

Тепер ми повинні визначитися з обмеженнями. Це означає, що ми повинні знайти ті значення х, які роблять будь-який знаменник рівним нулю.

• У тілі нашої роботи ми маємо знаменник (2x + 3) (2x − 3) (x + 4). Якщо ми встановимо це рівне нулю, властивість нульового добутку має на увазі, що $$2 x+3=0 \quad \text { or } \quad 2 x-3=0 \quad \text { or } \quad x+4=0$$

Кожен з цих лінійних факторів може бути вирішений самостійно $$x=-3 / 2 \quad \text { or } \quad x=3 / 2 \quad \text { or } \quad x=-4$$

Кожне з цих x-значень є обмеженням.

• У кінцевому раціональному вираженні знаменник дорівнює 2х + 3. Цей вираз дорівнює нулю, коли x = −3/2, і не надає нових обмежень.
• Оскільки знаменник вихідного виразу, а саме$4 x^{3}+16 x^{2}-9 x-36$, ідентичний його фактованої формі в тілі нашої роботи, цей знаменник не буде виробляти ніяких нових обмежень.

Таким чином, для всіх значень х $$\frac{2 x^{2}+5 x-12}{4 x^{3}+16 x^{2}-9 x-36}=\frac{1}{2 x+3}$$

за умови$x \neq −3/2, 3/2, or −4$. Це обмеження. Два вирази ідентичні для всіх інших значень x.

Нарешті, давайте перевіримо цей результат за допомогою нашого графічного калькулятора. Завантажте кожну сторону рівняння (18) у меню Y =, як показано на малюнку$\PageIndex{2}$ (а). Ми знаємо, що у нас є обмеження на x = −3/2, тому давайте встановимо TBLStart = −2 і$\Delta \mathrm{Tbl}=0.5$, як показано на малюнку$\PageIndex{2}$ (b). Переконайтеся, що у вас встановлено AUTO як для незалежних, так і для залежних змінних. Натисніть кнопку TABLE, щоб створити табличне відображення, показане на малюнку$\PageIndex{2}$ (c).

Малюнок$\PageIndex{2}$. Використовуючи графічний калькулятор, щоб перевірити, чи ліва та права сторони рівняння (18) ідентичні.

Пам'ятайте, що ми розмістили ліву та праву сторони рівняння (18) у Y1 та Y2 відповідно.

• На малюнку$\PageIndex{2}$ (c) зауважте, що вирази Y1 та Y2 узгоджуються з усіма значеннями x, окрім x = −1.5. Це обмеження −3/2, яке ми знайшли вище.
• Використовуйте клавішу зі стрілкою вниз, щоб прокрутити вниз таблицю, показану на малюнку$\PageIndex{2}$ (c), щоб створити табличний вигляд, показаний на малюнку$\PageIndex{2}$ (d). Зверніть увагу, що Y1 і Y2 згодні для всіх значень x, крім x = 1.5. Це обмеження 3/2 ми виявили вище.
• Ми залишаємо його нашим читачам, щоб розкрити обмеження на x = −4 за допомогою стрілки вгору для прокрутки таблиці вгору, доки ви не досягнете значення x −4. Вам слід розкрити інше повідомлення ERR (помилка) при цьому значенні x, оскільки це обмеження. Повідомлення ERR ви отримуєте через те, що знаменник лівого боку рівняння (18) дорівнює нулю при x = −4.

Зміни підпису

Це не рідкість, що вам доведеться маніпулювати знаками в дробі, щоб отримати загальні фактори, які потім можуть бути скасовані. Розглянемо, наприклад, раціональний вираз

$$\frac{3-x}{x-3}$$

Одним з можливих підходів є множник −1 з чисельника для отримання

$$\frac{3-x}{x-3}=\frac{-(x-3)}{x-3}$$

Тепер ви можете скасувати загальні фактори.

\[\frac{3-x}{x-3}=\frac{-(x-3)}{x-3}=\frac{-(x-3)}{x-3}=-1\]

Цей результат є дійсним для всіх значень x, наданих$x \neq 3$.

Давайте розглянемо інший приклад.

Приклад$\PageIndex{6}$

Звести раціональне вираження $$\frac{2 x-2 x^{3}}{3 x^{3}+4 x^{2}-3 x-4}$$ до найнижчих термінів. Зазначте всі обмеження.

Рішення

У чисельнику перерахуйте 2x, а потім завершіть факторизацію за допомогою різниці двох квадратів візерунка.

$$2 x-2 x^{3}=2 x\left(1-x^{2}\right)=2 x(1+x)(1-x)$$

Знаменник може бути врахований шляхом групування.

$$\begin{aligned} 3 x^{3}+4 x^{2}-3 x-4 &=x^{2}(3 x+4)-1(3 x+4) \\ &=\left(x^{2}-1\right)(3 x+4) \\ &=(x+1)(x-1)(3 x+4) \end{aligned}$$

Зверніть увагу, як різниця візерунка двох квадратів була застосована на останньому кроці.

На цьому етапі, $$\frac{2 x-2 x^{3}}{3 x^{3}+4 x^{2}-3 x-4}=\frac{2 x(1+x)(1-x)}{(x+1)(x-1)(3 x+4)}$$

Оскільки у нас є 1 − x у чисельнику та x − 1 у знаменнику, ми перерахуємо −1 з 1 − x, і оскільки порядок множників не впливає на їхній добуток, ми перемістимо −1 до передньої частини чисельника.

$$\frac{2 x-2 x^{3}}{3 x^{3}+4 x^{2}-3 x-4}=\frac{2 x(1+x)(-1)(x-1)}{(x+1)(x-1)(3 x+4)}=\frac{-2 x(1+x)(x-1)}{(x+1)(x-1)(3 x+4)}$$

Тепер ми можемо скасувати загальні фактори.

\[\begin{aligned} \frac{2 x-2 x^{3}}{3 x^{3}+4 x^{2}-3 x-4} &=\frac{-2 x(1+x)(x-1)}{(x+1)(x-1)(3 x+4)} \\ &=\frac{-2 x(1+x)(x-1)}{(x+1)(x-1)(3 x+4)} \\ &=\frac{-2 x}{3 x+4} \end{aligned}\]

Зверніть увагу, що x + 1 ідентичний 1 + x і скасовує. Таким чином,

$$\frac{2 x-2 x^{3}}{3 x^{3}+4 x^{2}-3 x-4}=\frac{-2 x}{3 x+4}$$

для всіх значень x, передбачених$x \neq-1,1,$ або$-4 / 3$. Це обмеження, значення х, які роблять знаменники рівними нулю.

Правило зміни знаків для дробів

Давайте розглянемо альтернативний підхід до останнього прикладу. Для початку поділимося припущенням про те, що кожен дріб має три знаки: один на чисельнику, один на знаменнику і третій на бруску дробу. Таким чином,

$$\frac{-2}{3} \quad \text { has understood signs } \quad+\frac{-2}{+3}$$

Викладемо правило зміни знаків для дробів.

Правило зміни знаків для дробів

Кожен дріб має три знаки: один на чисельнику, один на знаменнику і один на рядку дробу. Якщо ви не бачите явного знака, то розуміється знак плюс. Якщо звести нанівець будь-які дві з цих частин,

• чисельник і знаменник, або
• чисельник і рядок дробу, або
• бар дробу і знаменник,

тоді фракція залишається незмінною.

Наприклад, почнемо з −2/3, а потім зробимо два заперечення: чисельник і рядок дробу. Потім,

$$+\frac{-2}{+3}=-\frac{+2}{+3}, \quad \text { or with understood plus signs, } \quad \frac{-2}{3}=-\frac{2}{3}$$

Це звичний результат, оскільки негативні два, поділені на позитивну трійку, дорівнюють негативним двом третинам.

З іншого боку, ми можемо вирішити скасувати чисельник і знаменник. Тоді −2/3 стає

$$+\frac{-2}{+3}=\frac{+2}{-3}, \quad \text { or with understood plus signs, } \quad \frac{-2}{3}=\frac{2}{-3}$$

Знову знайомий результат. Звичайно, негативні два, розділені на позитивні три, такі ж, як позитивні два, розділені на негативні три. Вони обидва рівні мінус дві третини.

Отже, у вас є. Зведіть нанівець будь-які дві частини дробу і вона залишається незмінною. На поверхні це здається тривіальним зауваженням, але його можна добре використовувати при зменшенні раціональних виразів. Припустимо, наприклад, що ми беремо оригінальний раціональний вираз з Example$\PageIndex{6}$ і скасовуємо чисельник і рядок дробу.

$$\frac{2 x-2 x^{3}}{3 x^{3}+4 x^{2}-3 x-4}=-\frac{2 x^{3}-2 x}{3 x^{3}+4 x^{2}-3 x-4}$$

Зверніть увагу, як ми зробили дві зміни знаків. Ми заперечували дріб бар, ми заперечували чисельник$\left(-\left(2 x-2 x^{3}\right)=2 x^{3}-2 x\right)$, і залишив знаменник поодинці. Тому дріб незмінний відповідно до нашого правила зміни знаків.

Тепер, фактор і скасування загальних факторів (ми залишаємо кроки для наших читачів - вони схожі на ті, які ми взяли в прикладі$\PageIndex{6}$).

\[\begin{aligned} \frac{2 x-2 x^{3}}{3 x^{3}+4 x^{2}-3 x-4} &=-\frac{2 x^{3}-2 x}{3 x^{3}+4 x^{2}-3 x-4} \\ &=-\frac{2 x(x+1)(x-1)}{(x+1)(x-1)(3 x+4)} \\ &=-\frac{2 x(x+1)(x-1)}{(x+1)(x-1)(3 x+4)} \\ &=-\frac{2 x}{3 x+4} \end{aligned}\]

Але чи відповідає ця відповідь відповідь у рівнянні (22)? Це робить, як видно, зробивши два заперечення, дріб і чисельник.

$$-\frac{2 x}{3 x+4}=\frac{-2 x}{3 x+4}$$

Січна лінія

Розглянемо графік функції f що ми намалювали на малюнку$\PageIndex{3}$. Зауважте, що ми вибрали дві точки на графіку f, а саме (a, f (a)) і (x, f (x)), і ми провели через них лінію L, яку математики називають «січною лінією».

Малюнок$\PageIndex{3}$. Січна лінія проходить через (a, f (a)) і (x, f (x)).

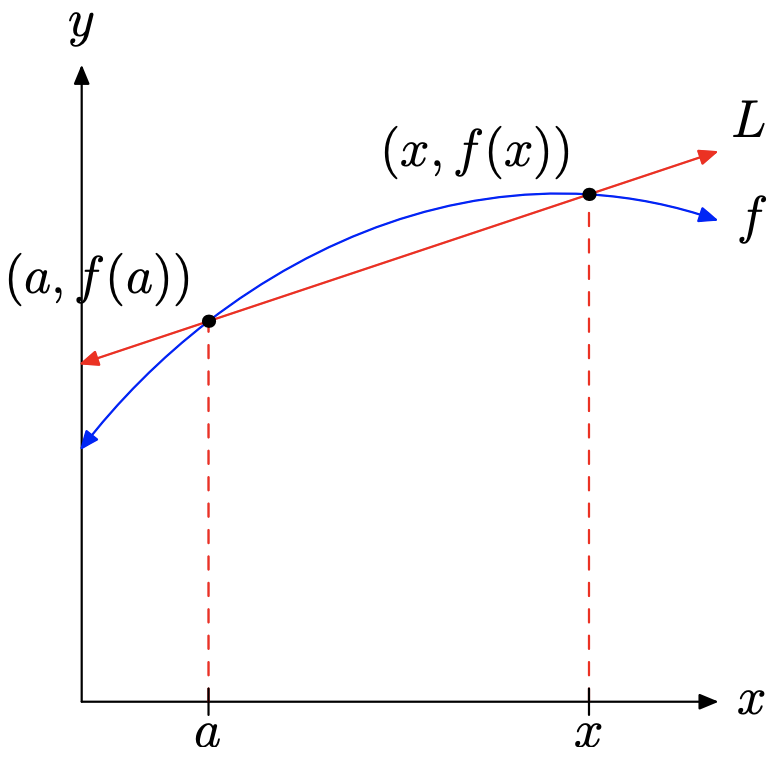
Нахил січної лінії L знаходять діленням зміни y на зміну x.

$$\text { Slope }=\frac{\Delta y}{\Delta x}=\frac{f(x)-f(a)}{x-a}$$

Цей нахил забезпечує середню швидкість зміни змінної y по відношенню до змінної x Студенти в обчисленні використовують цю «середню швидкість зміни» для розвитку поняття «миттєва швидкість зміни». Однак ми залишимо це завдання для студентів обчислення та зосередимося на задачі спрощення рівняння виразу (23) для середньої швидкості змін.

Приклад$\PageIndex{7}$

З огляду на функцію$f(x) = x^2$, спростити вираз для середньої швидкості зміни, а саме $$\frac{f(x)-f(a)}{x-a}$$

Рішення

По-перше, зверніть увагу, що$f(x)=x^{2}$ і$f(a)=a^{2},$ так ми можемо написати $$\frac{f(x)-f(a)}{x-a}=\frac{x^{2}-a^{2}}{x-a}$$

Тепер ми можемо використовувати різницю двох квадратів шаблону для множника чисельника та скасування загальних факторів.

\[\frac{x^{2}-a^{2}}{x-a}=\frac{(x+a)(x-a)}{x-a}=x+a\]

Таким чином, $$\frac{f(x)-f(a)}{x-a}=x+a$$

за умови, звичайно, що$x \neq a$.

Давайте розглянемо інший приклад.

Приклад$\PageIndex{8}$

Розглянемо функцію$f(x)=x^{2}-3 x-5$. Спростити $$\frac{f(x)-f(2)}{x-2}$$

Рішення

По-перше,$f(x)=x^{2}-3 x-5$ і тому$f(2)=(2)^{2}-3(2)-5=-7,$ так ми можемо написати

$$\frac{f(x)-f(2)}{x-2}=\frac{\left(x^{2}-3 x-5\right)-(-7)}{x-2}=\frac{x^{2}-3 x+2}{x-2}$$

Тепер ми можемо перерахувати чисельник і скасувати загальні фактори.

\[\frac{x^{2}-3 x+2}{x-2}=\frac{(x-2)(x-1)}{x-2}=x-1\]

Таким чином, $$\frac{f(x)-f(2)}{x-2}=x-1$$ за умови, звичайно, що$x \neq 2$.

Вправа

У вправах 1 - 12 зменшіть кожне раціональне число до найнижчих, застосовуючи наступні етапи:

1. Простий множник як чисельник, так і знаменник.
2. Скасувати загальні прості множники.
3. Спростити чисельник і знаменник результату.

Вправа$\PageIndex{1}$

$\frac{147}{98}$

Відповідь

$\frac{3}{2}$

Вправа$\PageIndex{2}$

$\frac{3087}{245}$

Вправа$\PageIndex{3}$

$\frac{1715}{196}$

Відповідь

$\frac{35}{4}$

Вправа$\PageIndex{4}$

$\frac{225}{50}$

Вправа$\PageIndex{5}$

$\frac{1715}{441}$

Відповідь

$\frac{35}{9}$

Вправа$\PageIndex{6}$

$\frac{56}{24}$

Вправа$\PageIndex{7}$

$\frac{108}{189}$

Відповідь

$\frac{4}{7}$

Вправа$\PageIndex{8}$

$\frac{75}{500}$

Вправа$\PageIndex{9}$

$\frac{100}{28}$

Відповідь

$\frac{25}{7}$

Вправа$\PageIndex{10}$

$\frac{98}{147}$

Вправа$\PageIndex{11}$

$\frac{1125}{175}$

Відповідь

$\frac{45}{7}$

Вправа$\PageIndex{12}$

$\frac{3087}{8575}$

У вправах 13 - 18 звести даний вираз до найнижчих. Зазначте всі обмеження.

Вправа$\PageIndex{13}$

$\frac{x^2−10x+9}{5x−5}$

Відповідь

$\frac{x−9}{5}$, за умови$x \ne 1$

Вправа$\PageIndex{14}$

$\frac{x^2−9x+20}{x^2−x−20}$

Вправа$\PageIndex{15}$

$\frac{x^2−2x−35}{x^2−7x}$

Відповідь

$\frac{x+5}{x}$, за умови$x \ne 0, 7$

Вправа$\PageIndex{16}$

$\frac{x^2−15x+54}{x^2+7x−8}$

Вправа$\PageIndex{17}$

$\frac{x^2+2x−63}{x^2+13x+42}$

Відповідь

$\frac{(x−7)(x+9)}{(x+7)(x+6)}$, за умови$x \ne −7, −6$

Вправа$\PageIndex{18}$

$\frac{x^2+13x+42}{9x+63}$

У вправах 19 - 24 звести нанівець будь-які дві частини дробу, потім множник (при необхідності) і скасувати загальні чинники, щоб звести раціональне вираження до найнижчих. Зазначте всі обмеження.

Вправа$\PageIndex{19}$

$\frac{x+2}{−x−2}$

Відповідь

−1, за умови$x \ne −2$

Вправа$\PageIndex{20}$

$\frac{4−x}{x−4}$

Вправа$\PageIndex{21}$

$\frac{2x−6}{3−x}$

Відповідь

−2, за умови$x \ne 3$

Вправа$\PageIndex{22}$

$\frac{3x+12}{−x−4}$

Вправа$\PageIndex{23}$

$\frac{3x^2+6x}{−x−2}$

Відповідь

−3x, надано$x \ne −2$

Вправа$\PageIndex{24}$

$\frac{8x−2x^2}{x−4}$

У вправах 25 - 38 звести кожне з заданих раціональних виразів до найнижчих. Зазначте всі обмеження.

Вправа$\PageIndex{25}$

$\frac{x^2−x−20}{25−x^2}$

Відповідь

$−\frac{x+4}{x+5}$, за умови$x \ne −5, 5$

Вправа$\PageIndex{26}$

$\frac{x−x^2}{x^2−3x+2}$

Вправа$\PageIndex{27}$

$\frac{x^2+3x−28}{x^2+5x−36}$

Відповідь

$\frac{x+7}{x+9}$, за умови$x \ne 4, −9$

Вправа$\PageIndex{28}$

$\frac{x^2+10x+9}{x^2+15x+54}$

Вправа$\PageIndex{29}$

$\frac{x^2−x−56}{8x−x^2}$

Відповідь

$−\frac{x+7}{x}$, за умови$x \ne 0, 8$

Вправа$\PageIndex{30}$

$\frac{x^2−7x+10}{5x−x^2}$

Вправа$\PageIndex{31}$

$\frac{x^2+13x+42}{x^2−2x−63}$

Відповідь

$−\frac{x+6}{x−9}$, за умови$x \ne −7, 9$

Вправа$\PageIndex{32}$

$\frac{x^2−16}{x^2−x−12}$

Вправа$\PageIndex{33}$

$\frac{x^2−9x+14}{49−x^2}$

Відповідь

$−\frac{x−2}{x+7}$, за умови$x \ne 7, −7$

Вправа$\PageIndex{34}$

$\frac{x^2+7x+12}{9−x^2}$

Вправа$\PageIndex{35}$

$\frac{x^2−3x−18}{x^2−6x+5}$

Відповідь

$\frac{(x−6)(x+3)}{(x−1)(x−5)}$, за умови$x \ne 1, 5$

Вправа$\PageIndex{36}$

$\frac{x^2+5x−6}{x^2−1}$

Вправа$\PageIndex{37}$

$\frac{x^2−3x−10}{−9x−18}$

Відповідь

$−\frac{x−5}{9}$, за умови$x \ne −2$

Вправа$\PageIndex{38}$

$\frac{x^2−6x+8}{16−x^2}$

У вправах 39 - 42 зведіть кожну раціональну функцію до найнижчих показників, а потім виконуйте кожне з наступних завдань.

1. Завантажте оригінальний раціональний вираз у Y1 та зменшений раціональний вираз (ваша відповідь) у Y2 вашого графічного калькулятора.
2. У TABLE SETUP встановіть TBLStart рівним нулю, ΔTbl дорівнює 1, а потім переконайтеся, що як незалежні, так і залежні змінні встановлені на Авто. Виберіть TABLE і прокручуйте за допомогою стрілок вгору і вниз на калькуляторі, поки не буде виявлено найменшого обмеження. Скопіюйте обидва стовпці таблиці на домашній папір, показуючи угоду між Y1 та Y2 та те, що відбувається при будь-яких обмеженнях.

Вправа$\PageIndex{39}$

$\frac{x^2−8x+7}{x^2−11x+28}$

Відповідь

$\frac{x−1}{x−4}$, за умови$x \ne 7, 4$

Вправа$\PageIndex{40}$

$\frac{x^2−5x}{x^2−9x}$

Вправа$\PageIndex{41}$

$\frac{8x−x^2}{x^2−x−56}$

Відповідь

$−\frac{x}{x+7}$, за умови$x \ne −7, 8$

Вправа$\PageIndex{42}$

$\frac{x^2+13x+40}{−2x−16}$

Задано f (x) = 2x+5, спростити кожне з виразів у вправах 43 - 46. Обов'язково зменшіть свою відповідь до найнижчих термінів і вкажіть будь-які обмеження.

Вправа$\PageIndex{43}$

$\frac{f(x)−f(3)}{x−3}$

Відповідь

2, за умови$x \ne 3$

Вправа$\PageIndex{44}$

$\frac{f(x)−f(6)}{x−6}$

Вправа$\PageIndex{45}$

$\frac{f(x)−f(a)}{x−a}$

Відповідь

2, за умови$x \ne a$

Вправа$\PageIndex{46}$

$\frac{f(a+h)−f(a)}{h}$

Дано$f(x) = x^2+2x$, спростити кожне з виразів у вправах 47 - 50. Обов'язково зменшіть свою відповідь до найнижчих термінів і вкажіть будь-які обмеження.

Вправа$\PageIndex{47}$

$\frac{f(x)−f(1)}{x−1}$

Відповідь

x+3, за умови$x \ne 1$

Вправа$\PageIndex{48}$

$\frac{f(x)−f(a)}{x−a}$

Вправа$\PageIndex{49}$

$\frac{f(a+h)−f(a)}{h}$

Відповідь

2а+ч+2, за умови$h \ne 0$

Вправа$\PageIndex{50}$

$\frac{f(x+h)−f(x)}{h}$

Дриль для майстерності. У вправах 51 - 54 оцініть задану функцію за заданим виразом і спростіть свою відповідь.

Вправа$\PageIndex{51}$

Припустимо, що f - функція

$f(x) = −\frac{x−6}{8x+7}$

Оцінити f (−3x+2) і спростити відповідь.

Відповідь

$−\frac{3x+4}{24x−23}$

Вправа$\PageIndex{52}$

Припустимо, що f - функція

$f(x) = −\frac{5x+3}{7x+6}$

Оцінити f (−5x+1) і спростити відповідь.

Вправа$\PageIndex{53}$

Припустимо, що f - функція

$f(x) = −\frac{3x−6}{4x+6}$

Оцінити f (−x−3) і спростити відповідь.

Відповідь

$−\frac{3x+15}{4x+6}$

Вправа$\PageIndex{54}$

Припустимо, що f - функція

$f(x) = \frac{4x−1}{2x−4}$

Оцініть f (5x) і спростіть свою відповідь.

​​​​​​​