6.7: Застосування факторингу

Last updated
Save as PDF

Page ID: 58292

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

У цьому розділі ми вирішимо додатки, рішення яких передбачають факторинг. Почнемо.

Приклад$\PageIndex{1}$

Прямокутна картина полотна вимірює$12$ дюйми на$16$ дюйми. Полотно монтується всередині рами рівномірної ширини, збільшуючи загальну площу покритого як полотном, так і каркасом до$396$ квадратних дюймів. Знайдіть рівномірну ширину рамки.

Рішення

Ми дотримуємося вимог до вирішення проблем Word.

Налаштуйте словник змінних: Ретельно позначена цифра допоможе нам зберегти нашу увагу. Ми дозволимо$x$ представляти рівномірну ширину кадру.

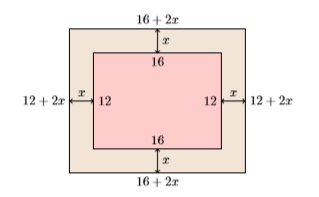
$рис. 6.7.1a.png$

Встановіть рівняння: Якщо внутрішні прямокутні розміри$16$ становлять$12$ дюйми на дюйми, додавання рамки рівномірної ширини$x$ робить розміри рами плюс полотно$16 + 2x$ дюймів на$12 + 2x$ дюйми. Загальна площа знаходить шляхом множення цих зовнішніх розмірів,$A = (16 + 2x)(12 + 2x)$. Якщо загальна площа дорівнює$A = 396$ квадратним дюймам, то маємо наступне рівняння. \[(16 + 2x)(12 + 2x) = 396 \nonumber \]
Вирішуємо рівняння: Починаємо з розширення правої частини рівняння. \[\begin{align*} (16 + 2x)(12 + 2x) &= 396\\ 192 + 56x +4x^2 &= 396 \end{align*} \nonumber \]Отримане рівняння нелінійне. Зробіть одну сторону нулем. \[4x^2 + 56x−204 = 0 \nonumber \]Ми могли б фактор$4$ на лівій стороні, але так як є нуль на правій стороні рівняння, це трохи простіше просто розділити обидві сторони на$4$. Зверніть увагу, як ми ділимо кожен член з лівого боку на число$4$. \[x^2 + 14x−51 = 0 \nonumber \]Нам потрібна ціла пара, добуток якої$ac = −51$ і чия сума дорівнює$b = 14$. Пара цілих чисел$−3,17$ приходить на розум. Оскільки коефіцієнт$x^2$ є одним, ми можемо просто «впустити на місце» нашу замовлену пару. \[(x−3)(x + 17) = 0 \nonumber \]Таким чином, рішення є$x = 3$ і$x = −17$.
Дайте відповідь на питання: рівномірна ширина рами не може бути$−17$ дюймами, тому ми виключаємо це рішення з розгляду. Значить, рівномірна ширина рами дорівнює$3$ дюймам.
Озирніться назад: Якщо рівномірна ширина кадру дорівнює$3$ дюймам, то кінцеві розміри будуть виглядати наступним чином.

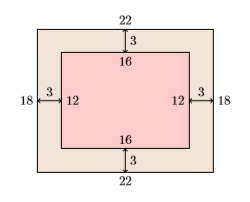
$рис. 6.7.1b.png$

Таким чином, об'єднана площа рами плюс полотно становить$A = (18)(22)$, або$A = 396$ квадратні дюйми, площа, наведена в постановці завдання. Наше рішення правильне.

Вправа$\PageIndex{1}$

Прямокутна картина полотна вимірює$7$ дюйми на$11$ дюйми. Полотно монтується всередині рами рівномірної ширини, збільшуючи загальну площу покритого як полотном, так і каркасом до$117$ квадратних дюймів. Знайдіть рівномірну ширину рамки.

Відповідь: $1$дюйм

Приклад$\PageIndex{2}$

Снаряд стріляє під кутом у повітря з вершини кліп з видом на океан. Відстань снаряда (у футах) від основи клізадається рівнянням,\[x = 120t \label{Eq6.7.1} \] а висота снаряда над рівнем моря (у футах) задається рівнянням,\[y = −16t^2 + 288t + 640 \label{Eq6.7.2} \] де$t$ - кількість часу (у секундах), що минув з моменту випуску снаряда.

Скільки часу проходить, перш ніж снаряд хлюпається в океан?
На той момент, як далеко знаходиться снаряд від основи клі?

Рішення

Ми дотримуємося вимог до вирішення проблем Word.

Налаштуйте словник змінних: змінні вже налаштовані для нас. \[\begin{align*} x &= \text {Distance from base of the cliff (in feet).}\\ y &= \text {Height above sea level (in feet).}\\ t &= \text {Time since projectile's release (in seconds).} \end{align*}\nonumber\]
Налаштування рівняння: Рівняння вже налаштовано (див. Рівняння\ ref {Eq6.7.1} і Рівняння\ ref {Eq6.7.2}).
Вирішіть рівняння: Коли снаряд хлюпається в океан, його висота над рівнем моря в цей момент становить$y = 0$ ноги. $0$Замініть$y$ в Equation\ ref {Eq6.7.2} і вирішіть отримане рівняння для$t$. \[\begin{align*} y &= -16t^2 + 288t + 640\\ 0 &= -16t^2 + 288t + 640 \end{align*}\nonumber\]Ми могли б врахувати$−16$, але так як ліва сторона цього рівняння дорівнює нулю, це трохи легше розділити обидві сторони на$−16$. Зверніть увагу, як ми ділимо кожен член з правого боку на$−16$. \[0=t^2 −18t−40 \nonumber \]Нам потрібна пара цілих чисел, щоб їх добуток$ac = −40$ і їх сума була$−18$. Пара цілих чисел$2$,$−20$ спадає на думку. Оскільки коефіцієнт$t^2$ є одним, ми можемо «падіння на місці» наша ціла пара. \[0=( t + 2)( t−20) \nonumber \]Значить, рішення є$t = −2$ і$t = 20$.
Відповідь на питання: Відповідаючи на питання (а),$t = −2$ секунди рішення не має сенсу. Таким чином, снаряд хлюпається в океан за$t = 20$ лічені секунди. При вирішенні питання (b), щоб знайти відстань снаряда від основи клів цей момент, підставити$t = 20$ в Equation\ ref {Eq6.7.1}. \[\begin{align*} x &= 120t\\ x &= 120(20)\\ x &= 2400 \end{align*}\nonumber\]Значить, в той момент, коли снаряд хлюпається в океан, він знаходиться в$2,400$ ногах від основи клі.
Озирніться назад: Найкраще, що ми можемо зробити тут, це перевірити наше рішення$t = 20$ в Equation\ ref {Eq6.7.2}. \[\begin{align*} y &= -16t^2 + 288t + 640 \\ y &= -16(20)2 + 288(20)+ 640 \\ y &= -6400+ 5760 + 640 \\ y &= 0 \end{align*}\nonumber\]Дійсно, в$t = 20$, снаряд дійсно хлюпається в океан.

Вправа$\PageIndex{2}$

Висота снаряда (в футах) задається рівнянням$y = −16t^2 + 144t + 576$, де час$t$ вимірюється в секундах. Скільки часу проходить до того, як снаряд вдариться об землю?

Відповідь: $12$секунд

Приклад$\PageIndex{3}$

Добуток двох послідовних парних чисел дорівнює$728$. Знайти цілі числа.

Рішення

Ми дотримуємося Вимоги до вирішення проблем Word.

Налаштувати словник змінних:$k$ Дозволяти представляти перше парне ціле число. Потім$k + 2$ представляє наступне послідовне парне ціле число.
Встановити рівняння: Добуток цілих чисел дорівнює$728$. Отже, ми маємо наступне рівняння. \[k(k + 2) = 728 \nonumber \]
Розв'яжіть рівняння: Розгорніть ліву частину рівняння. \[k^2 +2k = 728 \nonumber \]Рівняння нелінійне. Зробіть одну сторону нулем. \[k^2 +2k−728 = 0 \nonumber \]Див. розділ Використання калькулятора для допомоги$ac$ методу -Method. Нам потрібна ціла пара, добуток якої$ac = −728$ і чия сума дорівнює$b = 2$. Введіть$-728/X$$\mathrm{Y1}$, а потім налаштуйте таблицю (див. Рис.$\PageIndex{1}$).

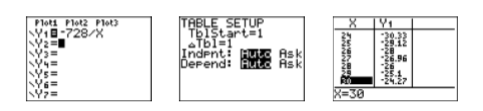
рис. 6.7.1.png — Малюнок$\PageIndex{1}$: Завантажити$ac/X$, або$-728/X$$\mathrm{Y1}$ в **меню Y=**.

Використовуйте клавіші зі стрілками вгору і вниз для прокрутки. Зверніть увагу, що$28,−26$ є бажаною парою. Оскільки коефіцієнт$k^2$ є одним, ми можемо «впустити на місце» впорядковану пару.

\[0=( k + 28)(k−26) \nonumber \]Значить, рішення є$k = −28$ і$k = 26$.

Дайте відповідь на питання: Якщо$k = −28$, наступне послідовне парне ціле число є$k +2=−26$. По-друге, якщо$k = 26$, наступне послідовне парне ціле число$k + 2 = 28$.
Озирніться назад: Наша перша пара - це$−28$ і$−26$. Вони мають необхідний продукт$728$. Друга наша пара -$26$ і$28$. Їх продукт теж є$728$. Обидва рішення перевіряємо!

Вправа$\PageIndex{3}$

Добуток двох послідовних натуральних непарних чисел дорівнює$483$. Знайти цілі числа.

Відповідь: $21$і$23$

Приклад$\PageIndex{4}$

Прямокутник має периметр$54$ футів і площа$180$ квадратних футів. Знайдіть розміри прямокутника.

Рішення

Ми дотримуємося Вимоги до вирішення проблем Word.

Налаштуйте змінний словник: ескіз допоможе нам зберегти фокус. $L$Дозволяти представляти довжину прямокутника і нехай$W$ представляють його ширину.

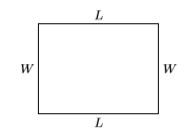
$рис. 6.7.2.png$

Встановіть рівняння: Периметр - це$54$ фути, отже$2W+2L = 54$, або розділивши обидві сторони\[W + L = 27 \label{Eq6.7.3} \] на$2$:$180$ Площа квадратних футів, отже:\[LW = 180 \label{Eq6.7.4}\]
Вирішити рівняння: Система рівнянь (рівняння\ ref {Eq6.7.3} і\ ref {Eq6.7.4}) може бути вирішена методом підстановки. Спочатку розв'яжіть рівняння\ ref {Eq6.7.3} для$W$:\[W = 27−L \label{Eq6.7.5}\] Заставте рівняння\ ref {Eq6.7.5} в Рівняння\ ref {Eq6.7.4}, розгорніть, а потім зробіть нуль з однієї сторони. \[\begin{align*} L(27-L) &= 180 \\ 27L-L^2 &= 180 \\ 0 &= L^2-27L+180 \end{align*}\nonumber\]Пара цілих чисел$−12,−15$ має$ac = 180$ добуток і суму$b = −27$. Крім того, коефіцієнт$L^2$ є один, так що ми можемо «падіння на місці» наша ціла пара. \[0=(L−12)(L−15) \nonumber \]Значить, рішення є$L = 12$ і$L = 15$.
Дайте відповідь на питання: Дві можливості по ширині.
1. $L = 12$Замінюємо в\ ref {Eq6.7.5}. \[\begin{align*} W &= 27-L \\ W &= 27-12 \\ W &= 15 \end{align*}\nonumber\]
2. $L = 15$Замінюємо в\ ref {Eq6.7.5}. \[\begin{align*} W &= 27-L \\ W &= 27-15 \\ W &= 12 \end{align*}\nonumber\]

Обидві відповіді дають однаковий$15$ прямокутник$12$ ноги, але ми зазвичай вважаємо термін «довжина» довшою стороною прямокутника.

Отже, давайте підемо з довжиною$L = 15$ ноги, а ширина -$W = 12$ ноги.

Озирніться назад: Давайте додамо$L = 15$ стопи і$W = 12$ ступні до діаграми.

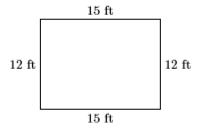
$рис. 6.7.3.png$

Якщо додати розміри навколо прямокутника, периметр$P = 15+12 +15+ 12$, або$P = 54$ фути, периметр, необхідний в постановці завдання.

Далі, якщо помножити розміри, то$A = (15)(12)$, або$A = 180$ квадратні фути, площа, необхідна в постановці завдання. Наше рішення правильне!

Вправа$\PageIndex{4}$

Прямокутник має периметр$62$ футів і площа$234$ квадратних футів. Знайдіть розміри прямокутника.

Відповідь: довжина =$18$ ноги і ширина =$13$ ноги