6.1: Найбільший загальний фактор

Ми починаємо цей розділ з визначень факторів і дільників. Тому що$24 = 2\cdot 12$, обидва$2$ і$12$ є чинниками$24$. Однак зверніть увагу, що також$2$ є дільником$24$, тому що при діленні$24$ на$2$ ви отримуєте$12$, з залишком нуля. Аналогічно, також$12$ є дільником$24$, тому що при діленні$24$ на$12$ ви отримуєте$2$, з залишком нуля.

Визначення: Фактори та дільники

Припустимо$n$,$m$ і є цілими числами. Тоді$m$ дільник (множник)$n$ if і тільки якщо існує інше ціле число$k$ так що$n=m \cdot k$.

Слова дільник і множник еквівалентні. Вони мають однакове значення.

Приклад$\PageIndex{1}$

Перерахуйте позитивні дільники (множники)$24$.

Рішення

Спочатку перерахуємо всі можливі способи, які ми можемо висловити$24$ як добуток двох натуральних чисел:

$$24=1 \cdot 24 \quad \text { or } \quad 24=2 \cdot 12 \quad \text { or } \quad 24=3 \cdot 8 \quad \text { or } \quad 24=4 \cdot 6 \nonumber$$

Тому позитивними дільниками (факторами)$24$ є$1,2,3,4,6,8,$ і$24$.

Вправа$\PageIndex{1}$

Перерахуйте позитивні дільники$18$.

Відповідь

$1,2,3,6,9,$і$18$

Приклад$\PageIndex{2}$

Перерахуйте позитивні дільники (фактори), які$36$ і$48$ мають спільне.

Рішення

Спочатку перерахуйте всі позитивні дільники (множники)$36$ і$48$ окремо, а потім коробку дільники, які є спільними.

Дільники$36$ є:$[1],[2],[3],[4],[6], 9, [12], 18, 36$

Дільники$48$ є:$[1],[2],[3],[4],[6], 8, [12], 16, 24, 48$

Тому загальними додатними дільниками (факторами)$36$ і$48$ є$1, 2, 3, 4, 6,$ і$12$.

Вправа$\PageIndex{2}$

Перерахуйте позитивні дільники, які$40$ і$60$ мають спільне.

Відповідь

$1,2,4,5,10,$і$20$

Визначення: Найбільший спільний дільник

Найбільший спільний дільник (коефіцієнт)$a$ і$b$ є найбільшим додатним числом, яке ділить рівномірно (без залишку) обидва$a$ і$b$. Найбільший спільний дільник$a$ і$b$ позначається символікою$\operatorname{GCD}(a, b)$. Ми також будемо використовувати абревіатуру,$\operatorname{GCF}(a, b)$ щоб представляє найбільший загальний фактор$a$ і$b$.

Пам'ятайте, найбільший спільний дільник і найбільший спільний фактор мають однакове значення. У прикладі$\PageIndex{2}$ ми перерахували загальні позитивні дільники$36$ і$48$. Найбільший з цих загальних дільників був$12$. Отже, найбільший спільний дільник (коефіцієнт)$36$ і$48$ є$12$, записаний$\operatorname{GCD}(36, 48)=12$.

При менших числах зазвичай легко визначити найбільший спільний дільник (множник).

Приклад$\PageIndex{3}$

Створіть найбільший спільний дільник (множник) кожної з наступних пар чисел:

1. $18$і$24$
2. $30$і$40$
3. $16$і$24$

Рішення

У кожному випадку ми повинні знайти максимально можливе додатне число, яке ділиться рівномірно на обидва задані числа.

1. Найбільше натуральне число, яке ділиться рівномірно на обидва$18$ і$24$ є$6$. Таким чином,$\operatorname{GCD}(18, 24)=6$.
2. Найбільше натуральне число, яке ділиться рівномірно на обидва$30$ і$40$ є$10$. Таким чином,$\operatorname{GCD}(30, 40)=10$.
3. Найбільше натуральне число, яке ділиться рівномірно на обидва$16$ і$24$ є$8$. Таким чином,$\operatorname{GCD}(16, 24)=8$.

Вправа$\PageIndex{3}$

Створіть найбільший спільний дільник$36$ і$60$.

Відповідь

$12$

При більших числах важче визначити найбільший спільний дільник (множник). Однак прайм-факторизація врятує день!

Приклад$\PageIndex{4}$

Знайти найбільший спільний дільник (коефіцієнт)$360$ і$756$.

Рішення

Простий фактор$360$ і$756$, написавши свою відповідь в експоненціальній формі.

Малюнок$\PageIndex{1}$

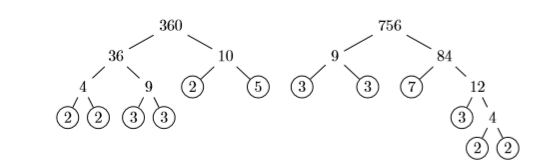
Таким чином:

$$\begin{array}{l}{360=2^{3} \cdot 3^{2} \cdot 5} \\ {756=2^{2} \cdot 3^{3} \cdot 7}\end{array} \nonumber$$

Примітка

Щоб знайти найбільший спільний дільник (множник), перерахуйте кожен фактор, який є спільним для найвищої потужності, яка є спільною.

У цьому випадку фактори$2$ і$3$ з'являються спільними, оскільки вони є$22$ найвищою силою$2$ і є$32$ найвищою силою$3$, що є спільними. Тому найбільшим спільним дільником$360$ і$756$ є:

$$\begin{aligned} \mathrm{GCD}(360,756) &=2^{2} \cdot 3^{2} \\ &=4 \cdot 9 \\ &=36 \end{aligned} \nonumber$$

Тому найбільшим спільним дільником (коефіцієнтом) є$\mathrm{GCD}(360,756)=36$. Зверніть увагу, що відбувається, коли ми запишемо кожне з заданих чисел як добуток найбільшого спільного фактора і другого фактора:

$$\begin{array}{l}{360={\color {Red} 36} \cdot 10} \\ {756={\color {Red} 36} \cdot 21}\end{array} \nonumber$$

У кожному конкретному випадку зверніть увагу на те, як другі другі фактори ($10$і$21$) не містять додаткових загальних факторів.

Вправа$\PageIndex{4}$

Знайдіть найбільший спільний дільник$120$ і$450$.

Відповідь

$30$

Пошук найбільшого спільного фактора мономов

Приклад$\PageIndex{4}$ показує техніку, яка використовується для пошуку найбільшого спільного фактора двох або більше мономов.

Знаходження GCF двох або більше мономов

Щоб знайти найбільший загальний коефіцієнт двох або більше мономов, дійте наступним чином:

1. Знайдіть найбільший спільний коефіцієнт (дільник) коефіцієнтів заданих мономов. При необхідності використовуйте просту факторизацію.
2. Перерахуйте кожну змінну, яка є спільною у заданих мономах.
3. Підніміть кожну змінну, яка з'являється спільною для вищої влади, яка з'являється спільною серед заданих мономів.

Приклад$\PageIndex{5}$

Знайдіть найбільший загальний фактор$6 x^{3} y^{3}$ і$9 x^{2} y^{5}$.

Рішення

Щоб знайти і,$\mathrm{GCF}$$6 x^{3} y^{3}$$9 x^{2} y^{5}$ зауважимо, що:

1. Найбільший спільний коефіцієнт (дільник)$6$ і$9$ є$3$.
2. У мономи$6x^3y^3$ і$9x^2y^5$ є змінні$x$ і$y$ загальні.
3. Найвища потужність$x$ спільного є$x^2$. Найвища потужність$y$ спільного є$y^3$.

Таким чином, найбільшим поширеним фактором є$\mathrm{GCF}\left(6 x^{3} y^{3}, 9 x^{2} y^{5}\right)=3 x^{2} y^{3}$. Зверніть увагу, що відбувається, коли ми пишемо кожен із заданих мономов як добуток найбільшого спільного фактора та другого мономіала:

$$\begin{array}{l}{6 x^{3} y^{3}={\color {Red} 3 x^{2} y^{3}} \cdot 2 x} \\ {9 x^{2} y^{5}={\color {Red} 3 x^{2} y^{3}} \cdot 3 y}\end{array} \nonumber$$

Зверніть увагу, що сукупність других мономіальних факторів ($2x$і$3y$) не містить додаткових загальних факторів.

Вправа$\PageIndex{5}$

Знайдіть найбільший загальний фактор$16xy^3$ і$12x^4y^2$.

Відповідь

$4 x y^{2}$

Приклад$\PageIndex{6}$

Знайдіть найбільший загальний фактор$12x^4$$18 x^3$, і$30 x^2$.

Рішення

Щоб знайти$\mathrm{GCF}$ з, і$12x^4$$18 x^3$, ми$30 x^2$ зауважимо, що:

1. Найбільший спільний коефіцієнт (дільник)$12$ of$18$, і$30$ є$6$.
2. Мономи$12x^4$$18 x^3$, і$30 x^2$ мають спільну$x$ змінну.
3. Найвища потужність$x$ спільного є$x^2$.

Таким чином, найбільшим поширеним фактором є$\mathrm{GCF}\left(12 x^{4}, 18 x^{3}, 30 x^{2}\right)=6 x^{2}$. Зверніть увагу, що відбувається, коли ми пишемо кожен із заданих мономов як добуток найбільшого спільного фактора та другого мономіала:

$$\begin{array}{l}{12 x^{4}={\color {Red}6 x^{2}} \cdot 2 x^{2}} \\ {18 x^{3}={\color {Red}6 x^{2}} \cdot 3 x} \\ {30 x^{2}={\color {Red}6 x^{2}} \cdot 5}\end{array} \nonumber$$

Зверніть увагу, що сукупність других мономіальних факторів ($2x^2$,$3 x$, і$5$) не містить додаткових загальних факторів.

Вправа$\PageIndex{6}$

Знайдіть найбільший загальний фактор$6y^3$$15 y^2$, і$9 y^5$.

Відповідь

$3 y^{2}$

Фактор з GCF

У главі 5 ми помножили мономіал і многочлен, розподіляючи мономіальні часи кожного члена в многочлені.

$$\begin{aligned} {\color {Red}2 x(}3 x^{2}+4 x-7{\color {Red})} &={\color {Red}2 x} \cdot 3 x^{2}+{\color {Red}2 x} \cdot 4 x-{\color {Red}2 x} \cdot 7 \\ &=6 x^{3}+8 x^{2}-14 x \end{aligned} \nonumber$$

У цьому розділі ми повертаємо цей процес множення. Ми представляємо вам кінцевий продукт і просимо повернути початкову проблему множення. У випадку$6 x^{3}+8 x^{2}-14 x$, найбільшим загальним фактором$6x^3$$8x^2$, і$14x$ є$2x$. Потім ми використовуємо розподільну властивість для перерахування$2x$ з кожного члена многочлена.

$$\begin{aligned} 6 x^{3}+8 x^{2}-14 x &={\color {Red}2 x} \cdot 3 x^{2}+{\color {Red}2 x} \cdot 4 x-{\color {Red}2 x} \cdot 7 \\ &={\color {Red}2 x(}3 x^{2}+4 x-7{\color {Red})} \end{aligned} \nonumber$$

Факторинг

Факторинг - це «немноження». Вам дається продукт, а потім просять знайти оригінальну проблему множення.

Перше правило факторингу

Якщо члени даного многочлена мають найбільший спільний коефіцієнт ($\mathrm{GCF}$), то коефіцієнт$\mathrm{GCF}$.

Давайте розглянемо кілька прикладів, які враховують$\mathrm{GCF}$.

Приклад$\PageIndex{7}$

Фактор:$6 x^{2}+10 x+14$

Рішення

Найбільший загальний фактор ($\mathrm{GCF}$) з$6x^2$,$10 x$ і$14$ є$2$. Фактор з$\mathrm{GCF}$.

$$\begin{aligned} 6 x^{2}+10x+14 x &={\color {Red}2 } \cdot 3 x^{2}+{\color {Red}2 } \cdot 5 x+{\color {Red}2 } \cdot 7 \\ &={\color {Red}2 (}3 x^{2}+5 x+7{\color {Red})} \end{aligned} \nonumber$$

Перевірка вашої роботи

Кожен раз, коли ви робите множник, перемножуйте, щоб перевірити свою роботу.

Перевірка: Множення. Розподіліть$2$.

$$\begin{aligned} {\color {Red}2 (}3 x^{2}+5 x+7{\color {Red})} &={\color {Red}2 } \cdot 3 x^{2}+{\color {Red}2 } \cdot 5 x+{\color {Red}2 } \cdot 7 \\ &=6 x^{2}+10 x+14 \end{aligned} \nonumber$$

Це початковий многочлен, тому ми правильно врахували.

Вправа$\PageIndex{7}$

Фактор:$9 y^{2}-15 y+12$

Відповідь

$3\left(3 y^{2}-5 y+4\right)$

Приклад$\PageIndex{8}$

Фактор:$12 y^{5}-32 y^{4}+8 y^{2}$

Рішення

Найбільший загальний фактор ($\mathrm{GCF}$) з$12y^5$,$32y^4$ і$8y^2$ є$4y^2$. Фактор з$\mathrm{GCF}$.

$$\begin{aligned} 12 y^{5}-32 y^{4}+8 y^{2} &={\color {Red}4 y^{2}} \cdot 3 y^{3}-{\color {Red}4 y^{2}} \cdot 8 y^{2}+{\color {Red}4 y^{2}} \cdot 2 \\ &={\color {Red}4 y^{2} (}3 y^{3}-8 y^{2}+2{\color {Red})} \end{aligned} \nonumber$$

Перевірка: Множення. Розподіліть мономіал$4y^2$.

$$\begin{aligned} {\color {Red}4 y^{2} (}3 y^{3}-8 y^{2}+2{\color {Red})} &={\color {Red}4 y^{2}} \cdot 3 y^{3}-{\color {Red}4 y^{2}} \cdot 8 y^{2}+{\color {Red}4 y^{2}} \cdot 2 \\ &=12 y^{5}-32 y^{4}+8 y^{2} \end{aligned} \nonumber$$

Це оригінальний многочлен. Ми правильно враховували.

Вправа$\PageIndex{8}$

Фактор:$8 x^{6}+20 x^{4}-24 x^{3}$

Відповідь

$4 x^{3}\left(2 x^{3}+5 x-6\right)$

Приклад$\PageIndex{9}$

Фактор:$12 a^{3} b+24 a^{2} b^{2}+12 a b^{3}$

Рішення

Найбільший загальний фактор ($\mathrm{GCF}$) з$12a^3b$,$24 a^2b^2$ і$12ab^3$ є$12ab$. Фактор з$\mathrm{GCF}$.

$$\begin{aligned} 12 a^{3} b+24 a^{2} b^{2}+12 a b^{3} &={\color {Red}12ab} \cdot a^{2}-{\color {Red}12ab} \cdot 2 a b+{\color {Red}12ab} \cdot b^{2} \\ &= {\color {Red}12ab (}a^{2}+2ab+b^{2}{\color {Red})} \end{aligned} \nonumber$$

Перевірка: Множення. Розподіліть мономіал$12ab$.

$$\begin{aligned} {\color {Red}12ab (}a^{2}+2ab+b^{2}{\color {Red})} &={\color {Red}12ab} \cdot a^{2}-{\color {Red}12ab} \cdot 2 a b+{\color {Red}12ab} \cdot b^{2} \\ &=12 a^{3} b+24 a^{2} b^{2}+12 a b^{3} \end{aligned} \nonumber$$

Це оригінальний многочлен. Ми правильно враховували.

Вправа$\PageIndex{9}$

Фактор:$15 s^{2} t^{4}+6 s^{3} t^{2}+9 s^{2} t^{2}$

Відповідь

$3 s^{2} t^{2}\left(5 t^{2}+2 s+3\right)$

Прискорення речей трохи

Врешті-решт, показавши свою роботу на ряді прикладів$\PageIndex{7}$$\PageIndex{8}$, таких як приклади$\PageIndex{9}$, і, вам потрібно буде навчитися виконувати процес подумки.

Приклад$\PageIndex{10}$

Коефіцієнт кожного з наступних многочленів:

1. $24 x+32$
2. $5 x^{3}-10 x^{2}-10 x$
3. $2 x^{4} y+2 x^{3} y^{2}-6 x^{2} y^{3}$

Рішення

У кожному конкретному випадку враховуйте найбільший загальний фактор ($\mathrm{GCF}$):

1. $\mathrm{GCF}$З$24x$ і$32$ є$8$. Таким чином, $$24x + 32 = 8(3x + 4) \nonumber$$
2. $\mathrm{GCF}$З$5x^3$$10 x^2$, і$10 x$ є$5x$. Таким чином: $$5 x^{3}-10 x^{2}-10 x=5 x\left(x^{2}-2 x-2\right) \nonumber$$
3. $\mathrm{GCF}$З$2x^4y$$2x^3y^2$, і$6x^2y^3$ є$2x^2y$. Таким чином: $$2 x^{4} y+2 x^{3} y^{2}-6 x^{2} y^{3}=2 x^{2} y\left(x^{2}+x y-3 y^{2}\right) \nonumber$$

Оскільки ви прискорюєте речі, подумки факторингу\(\mathrm{GCF}\), це ще важливіше, що ви перевіряєте свої результати. Перевірку також можна зробити подумки. Наприклад, перевіряючи третій результат, подумки розподіліть$2x^2y$ раз на кожен термін$x^2 +xy−3y^2$. Множення$2x^2y$ на перший член$x^2$ виробляє перший член$2x^4y$, перший член у початковому многочлені.

Продовжуйте таким чином, подумки перевіряючи$2x^2y$ добуток з кожним терміном$x^2 + xy −3y^2$, переконавшись, що кожен результат узгоджується з відповідним терміном початкового многочлена.

Вправа$\PageIndex{10}$

Фактор:$18 p^{5} q^{4}-30 p^{4} q^{5}+42 p^{3} q^{6}$

Відповідь

$6 p^{3} q^{4}\left(3 p^{2}-5 p q+7 q^{2}\right)$

Пам'ятайте, що розподільне властивість дозволяє нам витягнути$\mathrm{GCF}$ назовні перед виразом або витягнути його ззаду. В символах:

${\color {Red}a}b+{\color {Red}a}c={\color {Red}a}(b+c) \quad$або$\quad b{\color {Red}a}+c{\color {Red}a}=(b+c){\color {Red}a}$

Приклад$\PageIndex{11}$

Фактор:$2 x(3 x+2)+5(3 x+2)$

Рішення

У цьому випадку найбільшим загальним фактором ($\mathrm{GCF}$) є$3x + 2$.

$$\begin{aligned} 2x(3 x+2)+5(3 x+2) &=2x \cdot {\color {Red}(3 x+2)}+5 \cdot{\color {Red}(3 x+2)} \\ &=(2 x+5){\color {Red}(3 x+2)} \end{aligned} \nonumber$$

Через комутативного властивості множення однаково справедливо витягнути$\mathrm{GCF}$ назовні попереду.

$$\begin{aligned} 2x(3 x+2)+5(3 x+2) &=2x \cdot {\color {Red}(3 x+2)}+5 \cdot{\color {Red}(3 x+2)} \\ &={\color {Red}(3 x+2)} (2 x+5)\end{aligned}$$

Зауважте, що порядок факторів відрізняється від першого розв'язку, але через комутативну властивість множення порядок не має значення. Відповіді ті ж.

Вправа$\PageIndex{11}$

Фактор:$3 x^{2}(4 x-7)+8(4 x-7)$

Відповідь

$\left(3 x^{2}+8\right)(4 x-7)$

Приклад$\PageIndex{12}$

Фактор:$15 a(a+b)-12(a+b)$

Рішення

У цьому випадку найбільшим загальним фактором ($\mathrm{GCF}$) є$3(a + b)$.

$$\begin{aligned} 15 a(a+b)-12(a+b) &={\color {Red}3(a+b)} \cdot 5 a-{\color {Red}3(a+b)} \cdot 4 \\ &={\color {Red}3(a+b)}(5 a-4) \end{aligned} \nonumber$$

Альтернативне рішення:

Цілком можливо, що ви можете не помітити, що$15$ і$12$ діляться на$3$, враховуючи лише загальний фактор$a + b$.

$$\begin{aligned} 15 a(a+b)-12(a+b) &=15a\cdot {\color {Red}(a+b)} - 12\cdot {\color {Red}(a+b)} \\ &=(15a-12) {\color {Red}(a+b)}\end{aligned} \nonumber$$

Однак тепер потрібно помітити, що ви можете продовжувати, факторинг$3$ з обох$15a$ і$12$.

$=3(5 a-4)(a+b)$

Зауважте, що порядок факторів відрізняється від першого розв'язку, але через комутативну властивість множення порядок не має значення. Відповіді ті ж.

Вправа$\PageIndex{12}$

Фактор:$24 m(m-2 n)+20(m-2 n)$

Відповідь

$4(6 m+5)(m-2 n)$

Факторинг за групуванням

Навичка остаточного факторингу в цьому розділі включає чотиристрокові вирази. Методика факторингу чотиричленного виразу називається факторингом шляхом групування.

Приклад$\PageIndex{13}$

Фактор за групуванням:$x^{2}+8 x+3 x+24$

Рішення

Ми «групуємо» перший і другий терміни, зазначивши, що ми можемо враховувати обидва ці терміни.$x$ Потім ми «групуємо» третій і четвертий терміни, зазначивши, що ми можемо$3$ виходити з обох цих термінів.

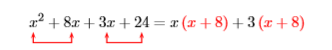
Тепер ми можемо$x + 8$ враховувати обидва ці терміни.

$(x+3){\color {Red}(x+8)}$

Вправа$\PageIndex{13}$

Фактор за групуванням:$x^{2}-6 x+2 x-12$

Відповідь

$(x+2)(x-6)$

Спробуємо угруповання, що містить деякі негативні ознаки.

Приклад$\PageIndex{14}$

Фактор за групуванням:$x^{2}+4 x-7 x-28$

Рішення

Ми «групуємо» перший і другий терміни, зазначивши, що ми можемо враховувати обидва ці терміни.$x$ Потім ми «групуємо» третій і четвертий члени, потім намагаємося фактор a$7$ з обох цих термінів.

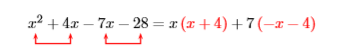
Це не призводить до загального фактору. Спробуємо ще раз, на цей раз факторинг a$−7$ з третього і четвертого термінів.

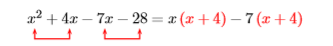
Це спрацювало! Тепер ми враховуємо загальний фактор$x + 4$.

$(x-7){\color {Red}(x+4)}$

Вправа$\PageIndex{14}$

Фактор за групуванням:$x^{2}-5 x-4 x+20$

Відповідь

$(x-4)(x-5)$

Давайте трохи збільшимо розмір чисел.

Приклад$\PageIndex{15}$

Фактор за групуванням:$6 x^{2}-8 x+9 x-12$

Рішення

Зауважте, що ми можемо перерахувати з перших двох термінів і$3$ з двох других.$2x$

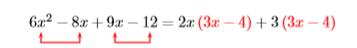
Тепер у нас є спільний фактор$3x−4$, який ми можемо врахувати.

$(2x+3){\color {Red}(3x-4)}$

Вправа$\PageIndex{15}$

Фактор за групуванням:$15 x^{2}+9 x+10 x+6$

Відповідь

$(3 x+2)(5 x+3)$

Оскільки числа стають більшими і більшими, вам потрібно враховувати ($\mathrm{GCF}$) з кожного угруповання. Якщо ні, ви не отримаєте загального фактора, щоб закінчити факторинг.

Приклад$\PageIndex{16}$

Фактор за групуванням:$24 x^{2}-32 x-45 x+60$

Рішення

Припустимо,$8x$ що ми враховуємо з перших двох термінів і$−5$ з двох других.

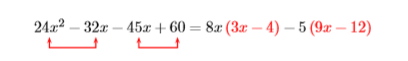
Це не спрацювало, оскільки у нас немає спільного фактора для завершення процесу факторингу. Однак зауважте, що ми все ще можемо врахувати$3$ від$9x−12$. Як ми вже враховували$5$, і тепер ми бачимо, що може фактор з додаткового$3$, це означає, що ми повинні були враховані$3$ раз$5$, або$15$, для початку. Почнемо знову, тільки на цей раз ми будемо$15$ враховувати з двох других термінів.

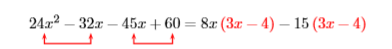
Красива! Тепер ми можемо врахувати$3x−4$.

$(8x-15){\color {Red}(3x-4)}$

Вправа$\PageIndex{16}$

Фактор за групуванням:$36 x^{2}-84 x+15 x-35$

Відповідь

$(12 x+5)(3 x-7)$