6.E: Факторинг (вправи)

6.1: Найбільший загальний фактор

У Вправах 1-6 перерахуйте всі позитивні дільники заданого числа, по порядку, від найменшого до найбільшого.

1)\(42\)

Відповідь

\(\{1,2,3,6,7,14,21,42\}\)

2)\(60\)

3)\(44\)

Відповідь

\(\{1,2,4,11,22,44\}\)

4)\(85\)

5)\(51\)

Відповідь

\(\{1,3,17,51\}\)

6)\(63\)

У Вправах 7-12 перерахуйте всі загальні позитивні дільники заданих чисел, по порядку, від найменшого до найбільшого.

7)\(36\) і\(42\)

Відповідь

\(\{1,2,3,6\}\)

8)\(54\) і\(30\)

9)\(78\) і\(54\)

Відповідь

\(\{1,2,3,6\}\)

10)\(96\) і\(78\)

11)\(8\) і\(76\)

Відповідь

\(\{1,2,4\}\)

12)\(99\) і\(27\)

У вправах 13-18 викласти найбільший спільний дільник заданих чисел.

13)\(76\) і\(8\)

Відповідь

\(4\)

14)\(84\) і\(60\)

15)\(32\) і\(36\)

Відповідь

\(4\)

16)\(64\) і\(76\)

17)\(24\) і\(28\)

Відповідь

\(4\)

18)\(63\) і\(27\)

У вправах 19-24 використовуйте просту факторизацію, щоб допомогти обчислити найбільший спільний дільник заданих чисел.

19)\(600\) і\(1080\)

Відповідь

\(120\)

20)\(150\) і\(120\)

21)\(1800\) і\(2250\)

Відповідь

\(450\)

22)\(540\) і\(150\)

23)\(600\) і\(450\)

Відповідь

\(150\)

24)\(4500\) і\(1800\)

У Вправах 25-36 знайдіть найбільший спільний фактор заданих виразів.

25)\(16b^{4}\) і\(56b^{9}\)

Відповідь

\(8b^{4}\)

26)\(28s^{2}\) і\(36s^{4}\)

27)\(35z^{2}\) і\(49z^{7}\)

Відповідь

\(7z^{2}\)

28)\(24w^{3}\) і\(30w^{8}\)

29)\(56x^{3} y^{4}\) і\(16x^{2} y^{5}\)

Відповідь

\(8 x^{2} y^{4}\)

30)\(35b^{5} c^{3}\) і\(63b^{4} c^{4}\)

31)\(24s^{4} t^{5}\) і\(16s^{3} t^{6}\)

Відповідь

\(8 s^{3} t^{5}\)

32)\(10v^{4} w^{3}\) і\(8v^{3} w^{4}\)

33)\(18 y^{7}\),\(45 y^{6}\), і\(27y^{5}\)

Відповідь

\(9 y^{5}\)

34)\(8 r^{7}\),\(24 r^{6}\), і\(12r^{5}\)

35)\(9 a^{6}\),\(6 a^{5}\), і\(15a^{4}\)

Відповідь

\(3 a^{4}\)

36)\(15 a^{5}\),\(24 a^{4}\), і\(24a^{3}\)

У вправах 37-52 перерахуйте\(\mathrm{GCF}\) з кожного з заданих виразів.

37)\(25 a^{2}+10 a+20\)

Відповідь

\(5\left(5 a^{2}+2 a+4\right)\)

38)\(40 c^{2}+15 c+40\)

39)\(35 s^{2}+25 s+45\)

Відповідь

\(5\left(7 s^{2}+5 s+9\right)\)

40)\(45 b^{2}+20 b+35\)

41)\(16 c^{3}+32 c^{2}+36 c\)

Відповідь

\(4 c\left(4 c^{2}+8 c+9\right)\)

42)\(12 b^{3}+12 b^{2}+18 b\)

43)\(42 s^{3}+24 s^{2}+18 s\)

Відповідь

\(6 s\left(7 s^{2}+4 s+3\right)\)

44)\(36 y^{3}+81 y^{2}+36 y\)

45)\(35 s^{7}+49 s^{6}+63 s^{5}\)

Відповідь

\(7 s^{5}\left(5 s^{2}+7 s+9\right)\)

46)\(35 s^{7}+56 s^{6}+56 s^{5}\)

47)\(14 b^{7}+35 b^{6}+56 b^{5}\)

Відповідь

\(7 b^{5}\left(2 b^{2}+5 b+8\right)\)

48)\(45 x^{5}+81 x^{4}+45 x^{3}\)

49)\(54 y^{5} z^{3}+30 y^{4} z^{4}+36 y^{3} z^{5}\)

Відповідь

\(6 y^{3} z^{3}\left(9 y^{2}+5 y z+6 z^{2}\right)\)

50)\(42 x^{4} y^{2}+42 x^{3} y^{3}+54 x^{2} y^{4}\)

51)\(45 s^{4} t^{3}+40 s^{3} t^{4}+15 s^{2} t^{5}\)

Відповідь

\(5.8^{2} t^{3}\left(9 s^{2}+8 s t+3 t^{2}\right)\)

52)\(20 v^{6} w^{3}+36 v^{5} w^{4}+28 v^{4} w^{5}\)

У вправах 53-60, перерахуйте\(\mathrm{GCF}\) з кожного з заданих виразів.

53)\(7 w(2 w-3)-8(2 w-3)\)

Відповідь

\((7 w-8)(2 w-3)\)

54)\(5 s(8 s-1)+4(8 s-1)\)

55)\(9 r(5 r-1)+8(5 r-1)\)

Відповідь

\((9 r+8)(5 r-1)\)

56)\(5 c(4 c-7)+2(4 c-7)\)

57)\(48 a(2 a+5)-42(2 a+5)\)

Відповідь

\(6(2 a+5)(8 a-7)\)

58)\(40 v(7 v-4)+72(7 v-4)\)

59)\(56 a(2 a-1)-21(2 a-1)\)

Відповідь

\(7(2 a-1)(8 a-3)\)

60)\(48 r(5 r+3)-40(5 r+3)\)

У вправах 61-68 коефіцієнт за групуванням. Не спрощуйте вираз перед факторингом.

61)\(x^{2}+2 x-9 x-18\)

Відповідь

\((x-9)(x+2)\)

62)\(x^{2}+6 x-9 x-54\)

63)\(x^{2}+3 x+6 x+18\)

Відповідь

\((x+6)(x+3)\)

64)\(x^{2}+8 x+7 x+56\)

65)\(x^{2}-6 x-3 x+18\)

Відповідь

\((x-3)(x-6)\)

66)\(x^{2}-3 x-9 x+27\)

67)\(x^{2}-9 x+3 x-27\)

Відповідь

\((x+3)(x-9)\)

68)\(x^{2}-2 x+7 x-14\)

У вправах 69-76 коефіцієнт за групуванням. Не спрощуйте вираз перед факторингом.

69)\(8 x^{2}+3 x-56 x-21\)

Відповідь

\((x-7)(8 x+3)\)

70)\(4 x^{2}+9 x-32 x-72\)

71)\(9 x^{2}+36 x-5 x-20\)

Відповідь

\((9 x-5)(x+4)\)

72)\(7 x^{2}+14 x-8 x-16\)

73)\(6 x^{2}-7 x-48 x+56\)

Відповідь

\((x-8)(6 x-7)\)

74)\(8 x^{2}-7 x-72 x+63\)

75)\(2 x^{2}+12 x+7 x+42\)

Відповідь

\((2 x+7)(x+6)\)

76)\(7 x^{2}+28 x+9 x+36\)

6.2: Вирішення нелінійних рівнянь

У вправах 1-8 розв'яжіть задане рівняння для\(x\).

1)\((9 x+2)(8 x+3)=0\)

Відповідь

\(x=-\dfrac{2}{9},-\dfrac{3}{8}\)

2)\((2 x-5)(7 x-4)=0\)

3)\(x(4 x+7)(9 x-8)=0\)

Відповідь

\(x=0,-\dfrac{7}{4}, \dfrac{8}{9}\)

4)\(x(9 x-8)(3 x+1)=0\)

5)\(-9 x(9 x+4)=0\)

Відповідь

\(x=0,-\dfrac{4}{9}\)

6)\(4 x(3 x-6)=0\)

7)\((x+1)(x+6)=0\)

Відповідь

\(x=-1,-6\)

8)\((x-4)(x-1)=0\)

У вправах 9-18, враховуючи, що ви вирішуєте для\(x\), введіть, чи є дане рівняння лінійним чи нелінійним. Не вирішуйте рівняння.

9)\(x^{2}+7 x=9 x+63\)

Відповідь

Нелінійний

10)\(x^{2}+9 x=4 x+36\)

11)\(6 x-2=5 x-8\)

Відповідь

Лінійний

12)\(-5 x+5=-6 x-7\)

13)\(7 x^{2}=-2 x\)

Відповідь

Нелінійний

14)\(4 x^{2}=-7 x\)

15)\(3 x^{2}+8 x=-9\)

Відповідь

Нелінійний

16)\(5 x^{2}-2 x=-9\)

17)\(-3 x+6=-9\)

Відповідь

Лінійний

18)\(8 x-5=3\)

У вправах 19-34 розв'яжіть кожне з заданих рівнянь для\(x\).

19)\(3 x+8=9\)

Відповідь

\(\dfrac{1}{3}\)

20)\(3 x+4=2\)

21)\(9 x^{2}=-x\)

Відповідь

\(x=0,-\dfrac{1}{9}\)

22)\(6 x^{2}=7 x\)

23)\(3 x+9=8 x+7\)

Відповідь

\(\dfrac{2}{5}\)

24)\(8 x+5=6 x+4\)

25)\(8 x^{2}=-2 x\)

Відповідь

\(x=0,-\dfrac{1}{4}\)

26)\(8 x^{2}=18 x\)

27)\(9 x+2=7\)

Відповідь

\(\dfrac{5}{9}\)

28)\(3 x+2=6\)

29)\(9 x^{2}=6 x\)

Відповідь

\(x=0, \dfrac{2}{3}\)

30)\(6 x^{2}=-14 x\)

31)\(7 x^{2}=-4 x\)

Відповідь

\(x=0,-\dfrac{4}{7}\)

32)\(7 x^{2}=-9 x\)

33)\(7 x+2=4 x+7\)

Відповідь

\(\dfrac{5}{3}\)

34)\(4 x+3=2 x+8\)

У вправах 35-50 множник шляхом групування вирішує кожне з заданих рівнянь для\(x\).

35)\(63 x^{2}+56 x+54 x+48=0\)

Відповідь

\(x=-\dfrac{6}{7},-\dfrac{8}{9}\)

36)\(27 x^{2}+36 x+6 x+8=0\)

37)\(16 x^{2}-18 x+40 x-45=0\)

Відповідь

\(x=-\dfrac{5}{2}, \dfrac{9}{8}\)

38)\(42 x^{2}-35 x+54 x-45=0\)

39)\(45 x^{2}+18 x+20 x+8=0\)

Відповідь

\(x=-\dfrac{4}{9},-\dfrac{2}{5}\)

40)\(18 x^{2}+21 x+30 x+35=0\)

41)\(x^{2}+10 x+4 x+40=0\)

Відповідь

\(x=-4,-10\)

42)\(x^{2}+11 x+10 x+110=0\)

43)\(x^{2}+6 x-11 x-66=0\)

Відповідь

\(x=11,-6\)

44)\(x^{2}+6 x-2 x-12=0\)

45)\(15 x^{2}-24 x+35 x-56=0\)

Відповідь

\(x=-\dfrac{7}{3}, \dfrac{8}{5}\)

46)\(12 x^{2}-10 x+54 x-45=0\)

47)\(x^{2}+2 x+9 x+18=0\)

Відповідь

\(x=-9,-2\)

48)\(x^{2}+8 x+4 x+32=0\)

49)\(x^{2}+4 x-8 x-32=0\)

Відповідь

\(x=8,-4\)

50)\(x^{2}+8 x-5 x-40=0\)

У вправах 51-54 виконайте кожне з наступних завдань:

1. Використовуйте строго алгебраїчну техніку для вирішення даного рівняння.
2. Використовуйте 5: intersect утиліту на графічному калькуляторі, щоб вирішити дане рівняння.

Повідомте про результати за допомогою графічного калькулятора, як показано у прикладі 6.2.7.

51)\(x^{2}=-4 x\)

Відповідь

\(x=-4,0\)

52)\(x^{2}=6 x\)

53)\(x^{2}=5 x\)

Відповідь

\(x=0,5\)

54)\(x^{2}=-6 x\)

У вправах 55-58 виконайте кожне з наступних завдань:

1. Використовуйте строго алгебраїчну техніку для вирішення даного рівняння.
2. Використовуйте 2: нуль утиліту на графічному калькуляторі, щоб вирішити дане рівняння.

Повідомте про результати, знайдені за допомогою графічного калькулятора, як показано у прикладі 6.2.8.

55)\(x^{2}+7 x=0\)

Відповідь

\(x=-7,0\)

56)\(x^{2}-8 x=0\)

57)\(x^{2}-3 x=0\)

Відповідь

\(x=0,3\)

58)\(x^{2}+2 x=0\)

6.3: Факторинг ax² + bx+c при a = 1

У Вправи 1-6 порівняйте заданий триноміал з\(ax^2 + bx + c\), а потім перерахуйте ВСІ цілі пари, добуток яких дорівнює\(ac\). Обведіть пару, сума якої дорівнює\(b\), а потім використовуйте цю пару, щоб допомогти множити заданий триноміал.

1)\(x^{2}+7 x-18\)

Відповідь

\((x-2)(x+9)\)

2)\(x^{2}+18 x+80\)

3)\(x^{2}-10 x+9\)

Відповідь

\((x-1)(x-9)\)

4)\(x^{2}+12 x+27\)

5)\(x^{2}+14 x+45\)

Відповідь

\((x+5)(x+9)\)

6)\(x^{2}+9 x+20\)

У Вправи 7-12 порівняйте заданий триноміал з\(ax^2 +bx+c\), а потім почніть перераховувати цілочисельні пари, добуток яких дорівнює\(ac\). Припиніть процес списку, коли ви виявите пару, сума якої дорівнює\(b\), потім обведіть і використовуйте цю пару, щоб допомогти множнику заданого триноміалу.

7)\(x^{2}-16 x+39\)

Відповідь

\((x-3)(x-13)\)

8)\(x^{2}-16 x+48\)

9)\(x^{2}-26 x+69\)

Відповідь

\((x-3)(x-23)\)

10)\(x^{2}-22 x+57\)

11)\(x^{2}-25 x+84\)

Відповідь

\((x-4)(x-21)\)

12)\(x^{2}+13 x-30\)

У вправах 13-18 порівняйте заданий триноміал з\(ax^2 + bx + c\), потім обчислите\(ac\). Спробуйте подумки виявити цілу пару, добуток якої\(ac\) і чия сума дорівнює\(b\). Фактор тріноміал, «скинувши цю пару на місце».

Примітка: Якщо ви виявите, що не можете ідентифікувати пару подумки, почніть перераховувати цілочисельні пари, чий продукт дорівнює\(ac\), а потім припиніть процес лістингу, коли ви зіткнетеся з парою, сума якої дорівнює\(b\).

13)\(x^{2}-13 x+36\)

Відповідь

\((x-4)(x-9)\)

14)\(x^{2}+x-12\)

15)\(x^{2}+10 x+21\)

Відповідь

\((x+3)(x+7)\)

16)\(x^{2}-17 x+66\)

17)\(x^{2}-4 x-5\)

Відповідь

\((x+1)(x-5)\)

18)\(x^{2}-20 x+99\)

У вправах 19-24 використовуйте алгебраїчну техніку для вирішення даного рівняння.

19)\(x^{2}=-7 x+30\)

Відповідь

\(x=3,-10\)

20)\(x^{2}=-2 x+35\)

21)\(x^{2}=-11 x-10\)

Відповідь

\(x=-1,-10\)

22)\(x^{2}=x+72\)

23)\(x^{2}=-15 x-50\)

Відповідь

\(x=-5,-10\)

24)\(x^{2}=-7 x-6\)

У вправах 25-30 використовуйте алгебраїчну техніку для вирішення даного рівняння.

25)\(60=x^{2}+11 x\)

Відповідь

\(x=4,-15\)

26)\(-92=x^{2}-27 x\)

27)\(-11=x^{2}-12 x\)

Відповідь

\(x=1,11\)

28)\(80=x^{2}-16 x\)

29)\(56=x^{2}+10 x\)

Відповідь

\(x=4,-14\)

30)\(66=x^{2}+19 x\)

У вправах 31-36 використовуйте алгебраїчну техніку для вирішення даного рівняння.

31)\(x^{2}+20=-12 x\)

Відповідь

\(x=-2,-10\)

32)\(x^{2}-12=11 x\)

33)\(x^{2}-36=9 x\)

Відповідь

\(x=-3,12\)

34)\(x^{2}+6=5 x\)

35)\(x^{2}+8=-6 x\)

Відповідь

\(x=-2,-4\)

36)\(x^{2}+77=18 x\)

У Вправи 37-40 виконайте кожне з наступних завдань:

1. Використовуйте строго алгебраїчну техніку для вирішення даного рівняння.
2. Використовуйте 5: intersect утиліту на графічному калькуляторі, щоб вирішити дане рівняння.

Повідомте про результати, знайдені за допомогою графічного калькулятора, як показано у прикладі 6.3.6.

37)\(x^{2}=x+12\)

Відповідь

\(x=-3,4\)

38)\(x^{2}=20-x\)

39)\(x^{2}+12=8 x\)

Відповідь

\(x=2,6\)

40)\(x^{2}+7=8 x\)

У вправах 41-44 виконайте кожне з наступних завдань:

1. Використовуйте строго алгебраїчну техніку для вирішення даного рівняння.
2. Використовуйте 2: нуль утиліту на графічному калькуляторі, щоб вирішити дане рівняння.

Повідомте про результати за допомогою графічного калькулятора, як показано у прикладі 6.3.7.

41)\(x^{2}-6 x-16=0\)

Відповідь

\(x=8,-2\)

42)\(x^{2}+7 x-18=0\)

43)\(x^{2}+10 x-24=0\)

Відповідь

\(x=-12,2\)

44)\(x^{2}-9 x-36=0\)

6.4: Факторинг ax² + bx+c при a1

У Вправи 1-6 порівняйте заданий триноміал з\(ax^2 + bx + c\), а потім перерахуйте ВСІ цілі пари, добуток яких дорівнює\(ac\). Обведіть пару, сума якої дорівнює\(b\), а потім використовуйте цю пару, щоб допомогти множити заданий триноміал.

1)\(6 x^{2}+13 x-5\)

Відповідь

\((2 x+5)(3 x-1)\)

2)\(3 x^{2}-19 x+20\)

3)\(4 x^{2}-x-3\)

Відповідь

\((x-1)(4 x+3)\)

4)\(6 x^{2}-23 x+7\)

5)\(3 x^{2}+19 x+28\)

Відповідь

\((x+4)(3 x+7)\)

6)\(2 x^{2}-9 x-18\)

У Вправи 7-12 порівняйте заданий триноміал з\(ax^2 +bx+c\), а потім почніть перераховувати цілочисельні пари, добуток яких дорівнює\(ac\). Припиніть процес списку, коли ви виявите пару, сума якої дорівнює\(b\), потім обведіть і використовуйте цю пару, щоб допомогти множнику заданого триноміалу.

7)\(12 x^{2}-23 x+5\)

Відповідь

\((3 x-5)(4 x-1)\)

8)\(8 x^{2}+22 x+9\)

9)\(6 x^{2}+17 x+7\)

Відповідь

\((2 x+1)(3 x+7)\)

10)\(4 x^{2}+19 x+21\)

11)\(3 x^{2}+4 x-32\)

Відповідь

\((x+4)(3 x-8)\)

12)\(4 x^{2}+x-14\)

У вправах 13-18 порівняйте заданий триноміал з\(ax^2 + bx + c\), потім обчислите\(ac\). Спробуйте подумки виявити цілу пару, добуток якої\(ac\) і чия сума дорівнює\(b\). Використовуйте цю пару, щоб допомогти фактор заданого триноміалу.

Примітка: Якщо ви виявите, що не можете ідентифікувати пару подумки, почніть перераховувати цілочисельні пари, чий продукт дорівнює\(ac\), а потім припиніть процес лістингу, коли ви зіткнетеся з парою, сума якої дорівнює\(b\).

13)\(3 x^{2}+28 x+9\)

Відповідь

\((3 x+1)(x+9)\)

14)\(6 x^{2}+x-1\)

15)\(4 x^{2}-21 x+5\)

Відповідь

\((x-5)(4 x-1)\)

16)\(4 x^{2}-x-14\)

17)\(6 x^{2}-11 x-7\)

Відповідь

\((3 x-7)(2 x+1)\)

18)\(2 x^{2}-17 x+21\)

У вправах 19-26 фактор тріноміала.

19)\(16 x^{5}-36 x^{4}+14 x^{3}\)

Відповідь

\(2 x^{3}(2 x-1)(4 x-7)\)

20)\(12 x^{4}-20 x^{3}+8 x^{2}\)

21)\(36 x^{4}-75 x^{3}+21 x^{2}\)

Відповідь

\(3 x^{2}(3 x-1)(4 x-7)\)

22)\(6 x^{4}-10 x^{3}-24 x^{2}\)

23)\(6 x^{4}-33 x^{3}+42 x^{2}\)

Відповідь

\(3 x^{2}(x-2)(2 x-7)\)

24)\(15 x^{3}-10 x^{2}-105 x\)

25)\(16 x^{4}-36 x^{3}-36 x^{2}\)

Відповідь

\(4 x^{2}(x-3)(4 x+3)\)

26)\(40 x^{4}-10 x^{3}-5 x^{2}\)

У вправах 27-38 використовуйте алгебраїчну техніку для вирішення даного рівняння.

27)\((10-8)^{2}-(7-5)^{3}\)

Відповідь

\(x=2,-\dfrac{9}{4}\)

28)\(2 x^{2}=7 x-3\)

29)\(3 x^{2}+16=-14 x\)

Відповідь

\(x=-2,-\dfrac{8}{3}\)

30)\(2 x^{2}-20=-3 x\)

31)\(3 x^{2}+30=23 x\)

Відповідь

\(x=6, \dfrac{5}{3}\)

32)\(6 x^{2}-7=-11 x\)

33)\(-7 x-3=-6 x^{2}\)

Відповідь

\(x=-\dfrac{1}{3}, \dfrac{3}{2}\)

34)\(13 x-45=-2 x^{2}\)

35)\(26 x-9=-3 x^{2}\)

Відповідь

\(x=-9, \dfrac{1}{3}\)

36)\(-23 x+7=-6 x^{2}\)

37)\(6 x^{2}=-25 x+9\)

Відповідь

\(x=\dfrac{1}{3},-\dfrac{9}{2}\)

38)\(2 x^{2}=13 x+45\)

У вправах 39-42 виконайте кожне з наступних завдань:

1. Використовуйте строго алгебраїчну техніку для вирішення даного рівняння.
2. Використовуйте 2: нуль утиліту на графічному калькуляторі, щоб вирішити дане рівняння.

Повідомте про результати, знайдені за допомогою графічного калькулятора, як показано у прикладі 6.4.5.

39)\(2 x^{2}-9 x-5=0\)

Відповідь

\(x=-\dfrac{1}{2},5\)

40)\(2 x^{2}+x-28=0\)

41)\(4 x^{2}-17 x-15=0\)

Відповідь

\(x=-\dfrac{3}{4},5\)

42)\(3 x^{2}+14 x-24=0\)

У вправах 43-46 виконайте кожне з наступних завдань:

1. Використовуйте строго алгебраїчну техніку для вирішення даного рівняння.
2. Використовуйте 2: нуль утиліту на графічному калькуляторі, щоб вирішити дане рівняння.

Повідомте про результати, знайдені за допомогою графічного калькулятора, як показано у прикладі 6.4.6.

43)\(2 x^{3}=3 x^{2}+20 x\)

Відповідь

\(x=0,-\dfrac{5}{2},4\)

44)\(2 x^{3}=3 x^{2}+35 x\)

45)\(10 x^{3}+34 x^{2}=24 x\)

Відповідь

\(x=0,-4, \dfrac{3}{5}\)

46)\(6 x^{3}+3 x^{2}=63 x\)

6.5: Факторингові спеціальні форми

У вправах 1-8 розгорніть кожне з заданих виразів.

1)\((8 r-3 t)^{2}\)

Відповідь

\(64 r^{2}-48 r t+9 t^{2}\)

2)\((6 a+c)^{2}\)

3)\((4 a+7 b)^{2}\)

Відповідь

\(16 a^{2}+56 a b+49 b^{2}\)

4)\((4 s+t)^{2}\)

5)\(\left(s^{3}-9\right)^{2}\)

Відповідь

\(s^{6}-18 s^{3}+81\)

6)\(\left(w^{3}+7\right)^{2}\)

7)\(\left(s^{2}+6 t^{2}\right)^{2}\)

Відповідь

\(s^{4}+12 s^{2} t^{2}+36 t^{4}\)

8)\(\left(7 u^{2}-2 w^{2}\right)^{2}\)

У вправах 9-28 множник кожного з заданих виразів.

9)\(25 s^{2}+60 s t+36 t^{2}\)

Відповідь

\((5 s+6 t)^{2}\)

10)\(9 u^{2}+24 u v+16 v^{2}\)

11)\(36 v^{2}-60 v w+25 w^{2}\)

Відповідь

\((6 v-5 w)^{2}\)

12)\(49 b^{2}-42 b c+9 c^{2}\)

13)\(a^{4}+18 a^{2} b^{2}+81 b^{4}\)

Відповідь

\(\left(a^{2}+9 b^{2}\right)^{2}\)

14)\(64 u^{4}-144 u^{2} w^{2}+81 w^{4}\)

15)\(49 s^{4}-28 s^{2} t^{2}+4 t^{4}\)

Відповідь

\(\left(7 s^{2}-2 t^{2}\right)^{2}\)

16)\(4 a^{4}-12 a^{2} c^{2}+9 c^{4}\)

17)\(49 b^{6}-112 b^{3}+64\)

Відповідь

\(\left(7 b^{3}-8\right)^{2}\)

18)\(25 x^{6}-10 x^{3}+1\)

19)\(49 r^{6}+112 r^{3}+64\)

Відповідь

\(\left(7 r^{3}+8\right)^{2}\)

20)\(a^{6}-16 a^{3}+64\)

21)\(5 s^{3} t-20 s^{2} t^{2}+20 s t^{3}\)

Відповідь

\(5 s t(s-2 t)^{2}\)

22)\(12 r^{3} t-12 r^{2} t^{2}+3 r t^{3}\)

23)\(8 a^{3} c+8 a^{2} c^{2}+2 a c^{3}\)

Відповідь

\(2 a c(2 a+c)^{2}\)

24)\(18 x^{3} z-60 x^{2} z^{2}+50 x z^{3}\)

25)\(-48 b^{3}+120 b^{2}-75 b\)

Відповідь

\(-3 b(4 b-5)^{2}\)

26)\(-45 c^{3}+120 c^{2}-80 c\)

27)\(-5 u^{5}-30 u^{4}-45 u^{3}\)

Відповідь

\(-5 u^{3}(u+3)^{2}\)

28)\(-12 z^{5}-36 z^{4}-27 z^{3}\)

У вправах 29-36 розгорніть кожне з заданих виразів.

29)\((21 c+16)(21 c-16)\)

Відповідь

\(441 c^{2}-256\)

30)\((19 t+7)(19 t-7)\)

31)\((5 x+19 z)(5 x-19 z)\)

Відповідь

\(25 x^{2}-361 z^{2}\)

32)\((11 u+5 w)(11 u-5 w)\)

33)\(\left(3 y^{4}+23 z^{4}\right)\left(3 y^{4}-23 z^{4}\right)\)

Відповідь

\(9 y^{8}-529 z^{8}\)

34)\(\left(5 x^{3}+z^{3}\right)\left(5 x^{3}-z^{3}\right)\)

35)\(\left(8 r^{5}+19 s^{5}\right)\left(8 r^{5}-19 s^{5}\right)\)

Відповідь

\(64 r^{10}-361 s^{10}\)

36)\(\left(3 u^{3}+16 v^{3}\right)\left(3 u^{3}-16 v^{3}\right)\)

У вправах 37-60 коефіцієнт кожного з заданих виразів.

37)\(361 x^{2}-529\)

Відповідь

\((19 x+23)(19 x-23)\)

38)\(9 b^{2}-25\)

39)\(16 v^{2}-169\)

Відповідь

\((4 v+13)(4 v-13)\)

40)\(81 r^{2}-169\)

41)\(169 x^{2}-576 y^{2}\)

Відповідь

\((13 x+24 y)(13 x-24 y)\)

42)\(100 y^{2}-81 z^{2}\)

43)\(529 r^{2}-289 s^{2}\)

Відповідь

\((23 r+17 s)(23 r-17 s)\)

44)\(49 a^{2}-144 b^{2}\)

45)\(49 r^{6}-256 t^{6}\)

Відповідь

\(\left(7 r^{3}+16 t^{3}\right)\left(7 r^{3}-16 t^{3}\right)\)

46)\(361 x^{10}-484 z^{10}\)

47)\(36 u^{10}-25 w^{10}\)

Відповідь

\(\left(6 u^{5}+5 w^{5}\right)\left(6 u^{5}-5 w^{5}\right)\)

48)\(a^{6}-81 c^{6}\)

49)\(72 y^{5}-242 y^{3}\)

Відповідь

\(2 y^{3}(6 y+11)(6 y-11)\)

50)\(75 y^{5}-147 y^{3}\)

51)\(1444 a^{3} b-324 a b^{3}\)

Відповідь

\(4 a b(19 a+9 b)(19 a-9 b)\)

52)\(12 b^{3} c-1875 b c^{3}\)

53)\(576 x^{3} z-1156 x z^{3}\)

Відповідь

\(4 x z(12 x+17 z)(12 x-17 z)\)

54)\(192 u^{3} v-507 u v^{3}\)

55)\(576 t^{4}-4 t^{2}\)

Відповідь

\(4 t^{2}(12 t+1)(12 t-1)\)

56)\(4 z^{5}-256 z^{3}\)

57)\(81 x^{4}-256\)

Відповідь

\(\left(9 x^{2}+16\right)(3 x+4)(3 x-4)\)

58)\(81 x^{4}-1\)

59)\(81 x^{4}-16\)

Відповідь

\(\left(9 x^{2}+4\right)(3 x+2)(3 x-2)\)

60)\(x^{4}-1\)

У вправах 61-68 коефіцієнт кожного з заданих виразів повністю.

61)\(z^{3}+z^{2}-9 z-9\)

Відповідь

\((z+3)(z-3)(z+1)\)

62)\(3 u^{3}+u^{2}-48 u-16\)

63)\(x^{3}-2 x^{2} y-x y^{2}+2 y^{3}\)

Відповідь

\((x+y)(x-y)(x-2 y)\)

64)\(x^{3}+2 x^{2} z-4 x z^{2}-8 z^{3}\)

65)\(r^{3}-3 r^{2} t-25 r t^{2}+75 t^{3}\)

Відповідь

\((r+5 t)(r-5 t)(r-3 t)\)

66)\(2 b^{3}-3 b^{2} c-50 b c^{2}+75 c^{3}\)

67)\(2 x^{3}+x^{2}-32 x-16\)

Відповідь

\((x+4)(x-4)(2 x+1)\)

68)\(r^{3}-2 r^{2}-r+2\)

У вправах 69-80 розв'яжіть кожне з заданих рівнянь для\(x\).

69)\(2 x^{3}+7 x^{2}=72 x+252\)

Відповідь

\(x=-6,6,-\dfrac{7}{2}\)

70)\(2 x^{3}+7 x^{2}=32 x+112\)

71)\(x^{3}+5 x^{2}=64 x+320\)

Відповідь

\(x=-8,8,-5\)

72)\(x^{3}+4 x^{2}=49 x+196\)

73)\(144 x^{2}+121=264 x\)

Відповідь

\(x=\dfrac{11}{12}\)

74)\(361 x^{2}+529=874 x\)

75)\(16 x^{2}=169\)

Відповідь

\(x=-\dfrac{13}{4}, \dfrac{13}{4}\)

76)\(289 x^{2}=4\)

77)\(9 x^{2}=25\)

Відповідь

\(x=-\dfrac{5}{3}, \dfrac{5}{3}\)

78)\(144 x^{2}=121\)

79)\(256 x^{2}+361=-608 x\)

Відповідь

\(x=-\dfrac{19}{16}\)

80)\(16 x^{2}+289=-136 x\)

У вправах 81-84 виконайте кожне з наступних завдань:

1. Використовуйте строго алгебраїчну техніку для вирішення даного рівняння.
2. Використовуйте 5: intersect утиліту на графічному калькуляторі, щоб вирішити дане рівняння.

Повідомте про результати за допомогою графічного калькулятора, як показано у прикладі 6.5.12.

81)\(x^{3}=x\)

Відповідь

\(x=0,-1,1\)

82)\(x^{3}=9 x\)

83)\(4 x^{3}=x\)

Відповідь

\(x=0,-\dfrac{1}{2},\dfrac{1}{2}\)

84)\(9 x^{3}=x\)

6.6: Стратегія факторингу

У вправах 1-12 множник кожного з заданих поліномів повністю.

1)\(484 y^{4} z^{2}-144 y^{2} z^{4}\)

Відповідь

\(4 y^{2} z^{2}(11 y+6 z)(11 y-6 z)\)

2)\(72 s^{4} t^{4}-242 s^{2} t^{6}\)

3)\(3 x^{7} z^{5}-363 x^{5} z^{5}\)

Відповідь

\(3 x^{5} z^{5}(x+11)(x-11)\)

4)\(5 r^{5} s^{2}-80 r^{3} s^{2}\)

5)\(2 u^{7}-162 u^{5}\)

Відповідь

\(2u^5(u + 9)(u−9) \)

6)\(405 x^{4}-320 x^{2}\)

7)\(3 v^{8}-1875 v^{4}\)

Відповідь

\(3v^4(v^2 + 25)(v + 5)(v−5)\)

8)\(3 a^{9}-48 a^{5}\)

9)\(3 x^{6}-300 x^{4}\)

Відповідь

\(3 x^{4}(x+10)(x-10)\)

10)\(2 y^{5}-18 y^{3}\)

11)\(1250 u^{7} w^{3}-2 u^{3} w^{7}\)

Відповідь

\(2 u^{3} w^{3}\left(25 u^{2}+w^{2}\right)(5 u+w)(5 u-w)\)

12)\(48 y^{8} z^{4}-3 y^{4} z^{8}\)

У вправах 13-24 коефіцієнт кожного з заданих поліномів повністю.

13)\(75 a^{6}-210 a^{5}+147 a^{4}\)

Відповідь

\(3 a^{4}(5 a-7)^{2}\)

14)\(245 v^{7}-560 v^{6}+320 v^{5}\)

15)\(180 a^{5} b^{3}+540 a^{4} b^{4}+405 a^{3} b^{5}\)

Відповідь

\(45 a^{3} b^{3}(2 a+3 b)^{2}\)

16)\(192 u^{6} v^{4}+432 u^{5} v^{5}+243 u^{4} v^{6}\)

17)\(2 b^{5}+4 b^{4}+2 b^{3}\)

Відповідь

\(2 b^{3}(b+1)^{2}\)

18)\(3 v^{6}+30 v^{5}+75 v^{4}\)

19)\(2 z^{4}-4 z^{3}+2 z^{2}\)

Відповідь

\(2 z^{2}(z-1)^{2}\)

20)\(2 u^{6}-40 u^{5}+200 u^{4}\)

21)\(324 x^{4}+360 x^{3}+100 x^{2}\)

Відповідь

\(4 x^{2}(9 x+5)^{2}\)

22)\(98 b^{4}+84 b^{3}+18 b^{2}\)

23)\(75 b^{4} c^{5}-240 b^{3} c^{6}+192 b^{2} c^{7}\)

Відповідь

\(3 b^{2} c^{5}(5 b-8 c)^{2}\)

24)\(162 a^{5} c^{4}-180 a^{4} c^{5}+50 a^{3} c^{6}\)

У вправах 25-36 коефіцієнт кожного з заданих поліномів повністю.

25)\(5 a^{5}+5 a^{4}-210 a^{3}\)

Відповідь

\(5 a^{3}(a-6)(a+7)\)

26)\(3 y^{5}-9 y^{4}-12 y^{3}\)

27)\(3 y^{6}-39 y^{5}+120 y^{4}\)

Відповідь

\(3 y^{4}(y-8)(y-5)\)

28)\(3 y^{7}-27 y^{6}+42 y^{5}\)

29)\(3 z^{4}+12 z^{3}-135 z^{2}\)

Відповідь

\(3 z^{2}(z-5)(z+9)\)

30)\(5 a^{4}-40 a^{3}-45 a^{2}\)

31)\(4 a^{6}+64 a^{5}+252 a^{4}\)

Відповідь

\(4 a^{4}(a+9)(a+7)\)

32)\(4 x^{4}+64 x^{3}+252 x^{2}\)

33)\(3 z^{4}+33 z^{3}+84 z^{2}\)

Відповідь

\(3 z^{2}(z+7)(z+4)\)

34)\(5 a^{6}+65 a^{5}+180 a^{4}\)

35)\(5 z^{7}-75 z^{6}+270 z^{5}\)

Відповідь

\(5 z^{5}(z-6)(z-9)\)

36)\(3 y^{4}-27 y^{3}+24 y^{2}\)

У вправах 37-48 коефіцієнт кожного з заданих поліномів повністю.

37)\(4 b^{3}-22 b^{2}+30 b\)

Відповідь

\(2 b(2 b-5)(b-3)\)

38)\(4 b^{6}-22 b^{5}+30 b^{4}\)

39)\(2 u^{4} w^{5}-3 u^{3} w^{6}-20 u^{2} w^{7}\)

Відповідь

\(u^{2} w^{5}(u-4 w)(2 u+5 w)\)

40)\(12 x^{5} z^{2}+9 x^{4} z^{3}-30 x^{3} z^{4}\)

41)\(12 x^{4} y^{5}+50 x^{3} y^{6}+50 x^{2} y^{7}\)

Відповідь

\(2 x^{2} y^{5}(3 x+5 y)(2 x+5 y)\)

42)\(24 s^{4} t^{3}+62 s^{3} t^{4}+40 s^{2} t^{5}\)

43)\(12 x^{3}+9 x^{2}-30 x\)

Відповідь

\(3 x(4 x-5)(x+2)\)

44)\(6 v^{4}+2 v^{3}-20 v^{2}\)

45)\(8 u^{6}+34 u^{5}+30 u^{4}\)

Відповідь

\(2 u^{4}(4 u+5)(u+3)\)

46)\(4 a^{4}+29 a^{3}+30 a^{2}\)

47)\(12 a^{4} c^{4}-35 a^{3} c^{5}+25 a^{2} c^{6}\)

Відповідь

\(a^{2} c^{A}(4 a-5 c)(3 a-5 c)\)

48)\(18 x^{6} z^{5}-39 x^{5} z^{6}+18 x^{4} z^{7}\)

У вправах 49-56 множник кожного з заданих поліномів повністю.

49)\(12 y^{5}+15 y^{4}-108 y^{3}-135 y^{2}\)

Відповідь

\(3 y^{2}(y+3)(y-3)(4 y+5)\)

50)\(9 b^{8}+12 b^{7}-324 b^{6}-432 b^{5}\)

51)\(9 x^{6} z^{5}+6 x^{5} z^{6}-144 x^{4} z^{7}-96 x^{3} z^{8}\)

Відповідь

\(3 x^{3} z^{5}(x+4 z)(x-4 z)(3 x+2 z)\)

52)\(12 u^{7} w^{3}+9 u^{6} w^{4}-432 u^{5} w^{5}-324 u^{4} w^{6}\)

53)\(72 z^{6}+108 z^{5}-2 z^{4}-3 z^{3}\)

Відповідь

\(z^{3}(6 z+1)(6 z-1)(2 z+3)\)

54)\(216 x^{7}+324 x^{6}-6 x^{5}-9 x^{4}\)

55)\(144 a^{6} c^{3}+360 a^{5} c^{4}-4 a^{4} c^{5}-10 a^{3} c^{6}\)

Відповідь

\(2 a^{3} c^{3}(6 a+c)(6 a-c)(2 a+5 c)\)

56)\(48 a^{8} c^{4}+32 a^{7} c^{5}-3 a^{6} c^{6}-2 a^{5} c^{7}\)

У Вправи 57-60 використовуйте калькулятор, щоб допомогти фактор кожного з заданих триномів. Дотримуйтесь плану процедури в Використання калькулятора для допомоги\(ac\) методу.

57)\(6 x^{2}+61 x+120\)

Відповідь

\((2 x+15)(3 x+8)\)

58)\(16 x^{2}-62 x-45\)

59)\(60 x^{2}-167 x+72\)

Відповідь

\((15 x-8)(4 x-9)\)

60)\(28 x^{2}+x-144\)

6.7: Застосування факторингу

1) Прямокутна картина полотна вимірює\(14\) дюйми на\(36\) дюйми. Полотно монтується всередині рами рівномірної ширини, збільшуючи загальну площу покритого як полотном, так і каркасом до\(720\) квадратних дюймів. Знайдіть рівномірну ширину рамки.

Відповідь

\(2\)дюймів

2) Прямокутна картина полотна вимірює\(10\) дюйми на\(32\) дюйми. Полотно монтується всередині рами рівномірної ширини, збільшуючи загальну площу покритого як полотном, так і каркасом до\(504\) квадратних дюймів. Знайдіть рівномірну ширину рамки.

3) Снаряд стріляє під кутом у повітря з вершини кліз видом на океан. Відстань снаряда (у футах) від основи клізадається рівнянням,\[x = 180t \nonumber \] а висота снаряда над рівнем моря (у футах) задається рівнянням,\[y = −16t^2 + 352t + 1664 \nonumber \] де\(t\) - кількість часу (у секундах), що минув з моменту випуску снаряда. Скільки часу проходить, перш ніж снаряд хлюпається в океан? На той момент, як далеко знаходиться снаряд від основи клі?

Відповідь

\(26\)секунди,\(4,680\) ноги

4) Снаряд стріляє під кутом у повітря з вершини кліз видом на океан. Відстань снаряда (у футах) від основи клізадається рівнянням,\[x = 140t \nonumber \] а висота снаряда над рівнем моря (у футах) задається рівнянням,\[y = −16t^2 + 288t + 1408 \nonumber \] де\(t\) - кількість часу (у секундах), що минув з моменту випуску снаряда. Скільки часу проходить, перш ніж снаряд хлюпається в океан? На той момент, як далеко знаходиться снаряд від основи клі?

5) Добуток двох послідовних парних цілих чисел дорівнює\(624\). Знайти цілі числа.

Відповідь

\(-26\)і\(−24\),\(24\) і\(26\)

6) Добуток двох послідовних парних цілих чисел дорівнює\(528\). Знайти цілі числа.

7) Добуток двох послідовних натуральних чисел дорівнює\(552\). Знайти цілі числа.

Відповідь

\(23\),\(24\)

8) Добуток двох послідовних натуральних чисел дорівнює\(756\). Знайти цілі числа.

9) Добуток двох послідовних непарних цілих чисел дорівнює\(483\). Знайти цілі числа.

Відповідь

\(−23\)і\(−21\),\(21\) і\(23\)

10) Добуток двох послідовних непарних цілих чисел дорівнює\(783\). Знайти цілі числа.

11) Прямокутник має периметр\(42\) футів і площа\(104\) квадратних футів. Знайдіть розміри прямокутника.

Відповідь

\(8\)ноги за\(13\) ногами

12) Прямокутник має периметр\(32\) футів і площа\(55\) квадратних футів. Знайдіть розміри прямокутника.

13) Радіус зовнішнього кола на один дюйм більше, ніж в два рази більше радіуса внутрішнього кола.

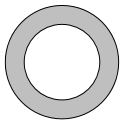
Якщо площа затіненої області\(40\pi \) квадратних дюймів, яка довжина внутрішнього радіуса?

Відповідь

\(3\)дюймів

14) Радіус зовнішнього кола на два дюйми довше, ніж в три рази більше радіуса внутрішнього кола.

Якщо площа затіненої області\(180\pi \) квадратних дюймів, яка довжина внутрішнього радіуса?

15) У вас є два позитивних числа. Друге число в три більше, ніж два рази більше першого числа. Різниця їх квадратів є\(144\). Знайдіть обидва додатних числа.

Відповідь

\(5\)і\(13\)

16) У вас є два позитивних числа. Друге число в два більше, ніж втричі більше першого числа. Різниця їх квадратів є\(60\). Знайдіть обидва додатних числа.

17) Два числа відрізняються на\(5\). Сума їх квадратів дорівнює\(97\). Знайдіть два числа.

Відповідь

\(4\)і\(9\),\(−4\) і\(−9\)

18) Два числа відрізняються на\(6\). Сума їх квадратів дорівнює\(146\). Знайдіть два числа.

19) Довжина прямокутника на три фути більше, ніж в шість разів його ширина. Якщо площа прямокутника\(165\) квадратних футів, яка ширина прямокутника?

Відповідь

\(5\)ноги

20) Довжина прямокутника на три фути довше, ніж в дев'ять разів більше його ширини. Якщо площа прямокутника\(90\) квадратних футів, яка ширина прямокутника?

21) Відношення ширини до довжини заданого прямокутника\(2\) дорівнює\(3\), або\(\dfrac {2}{3}\). Якщо ширина і довжина збільшені на\(4\) дюйми, площа отриманого прямокутника дорівнює\(80\) квадратним дюймам. Знайдіть ширину і довжину вихідного прямокутника.

Відповідь

\(4\)дюйми на\(6\) дюйми

22) Відношення ширини до довжини заданого прямокутника\(3\) дорівнює\(4\), або\(\dfrac {3}{4}\). Якщо ширина збільшена на\(3\) дюйми, а довжина збільшена на\(6\) дюйми, площа отриманого прямокутника -\(126\) квадратні дюйми. Знайдіть ширину і довжину вихідного прямокутника.